基于瞬时对称分量法的电网无功补偿方法

车学哲，沈凤龙，王建辉，朴贤国

（东北大学信息科学与工程学院，沈阳110819）

近年来，随着冶金工厂中电弧炉容量的不断增加，电弧炉炼钢对电网的干扰愈发严重。交流电弧炉在炉料熔化期，经常发生短路，造成电网电压的不规则波动。当断弧时，取自电网的有功功率等于零，炉子消耗的无功功率最大，无功电流大幅度变动和不稳定，引起了供电系统电抗压降变化，结果也会造成电压波动。此外，由于电弧本身还具有整流效应，因此会产生出高次谐波电流，回馈到电网中，导致电网中电压波形畸变，中性点位移。同时由于每相电弧长度变化在时间上不一致，会造成电压闪烁［1］。

为抑制电弧炉运行对配电网电压的影响，国内外学者提出了许多无功补偿器［2］。文献［3］提出可以在配电网中安装基于电力电子技术的静止无功补偿器SVG，采用SVG能抑制各种陡然变化的电压波动和电压闪烁，但是装置的实时应答特性不好。本文说明了如何利用SVG进行实时的无功补偿，并重点研究了瞬时对称分量法。

1 瞬时对称分量法

1.1 瞬时无功理论基础

传统的功率算法需测量相角，是基于相量进行计算的，因而数字测量系统不能实时算出系统功率。外国学者赤木泰文提出的瞬时无功理论，是利用系统电压电流的瞬时值进行计算，不需考虑相角问题，将系统功率的实时计算向前推进了一大步。下面给出瞬时无功理论的经典公式（pq变换）：

其中eα、eβ、iα、iβ是将三相电压电流的瞬时值经过克拉克变换，变换到αβ坐标系下的值。

瞬时无功理论应用于三相平衡系统时，得到的p、q是直流量，可表示瞬时求出传统功率定义下系统有功和无功的有效值。但瞬时无功理论应用于三相不平衡系统时，得到的p、q并不是直流量，而是含有直流分量的正弦波，与传统功率定义不符，不利于实时分析。

1.2 瞬时对称分量法求取瞬时功率

对于三相不平衡系统，为解决瞬时无功理论实时求取功率的问题，本文提出将瞬时无功理论与瞬时对称分量法相结合来实时求取功率的方法。

首先利用瞬时对称分量法，将三相电压电流瞬时值计算出序分量。

瞬时对称分量法充分利用三相电压电流瞬时值获取序分量。

三相 －单相变换公式如下：

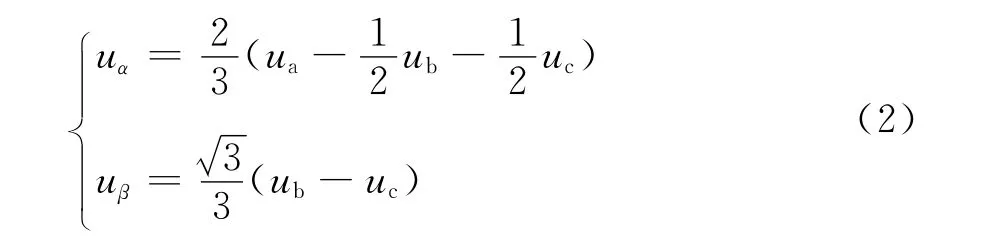
式中：ua、ub和uc为三相电压或电流；uα和uβ为αβ平面上电压或电流。

图1 平面上的三相电压矢量图Fig.1 Three－phase voltage vector on the plane

在t和t＋Δt时刻有

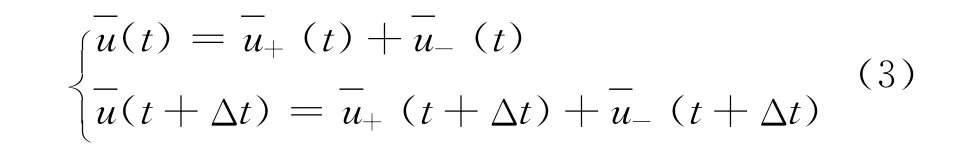
不失一般性，令t时刻，正序负序矢量分别为

则有下式成立

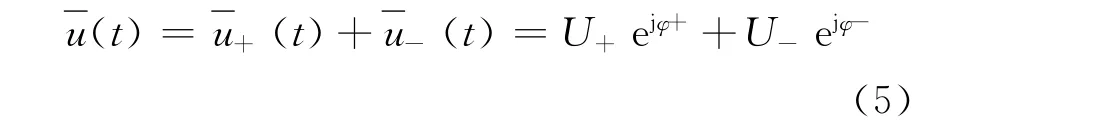
同样，在t＋Δt时刻，有

联立求解式（3）、式（4）和式（6），并令Δt趋于无穷小，有

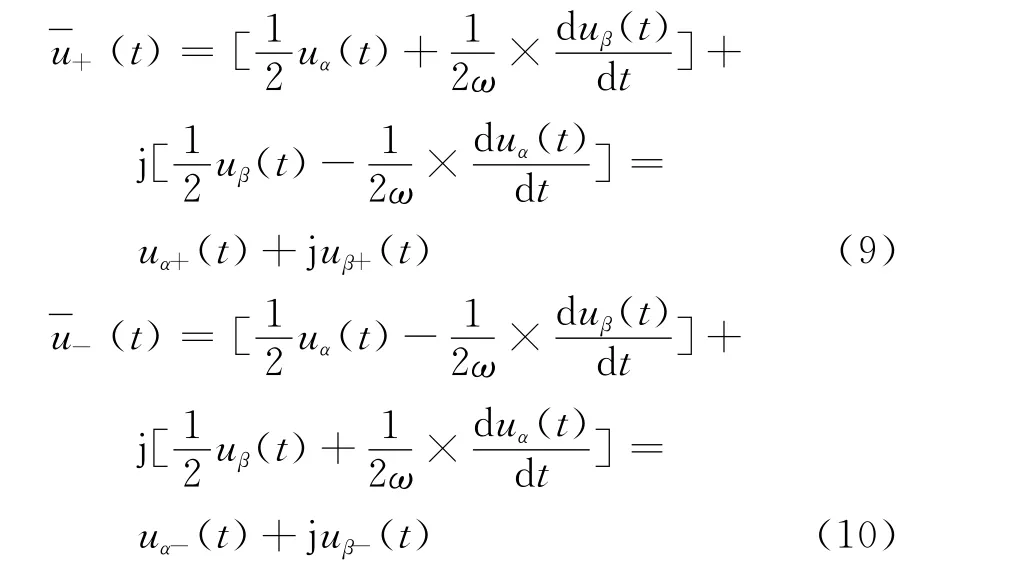
这样就可以求出三相电压的基波正序分量和基波负序分量：

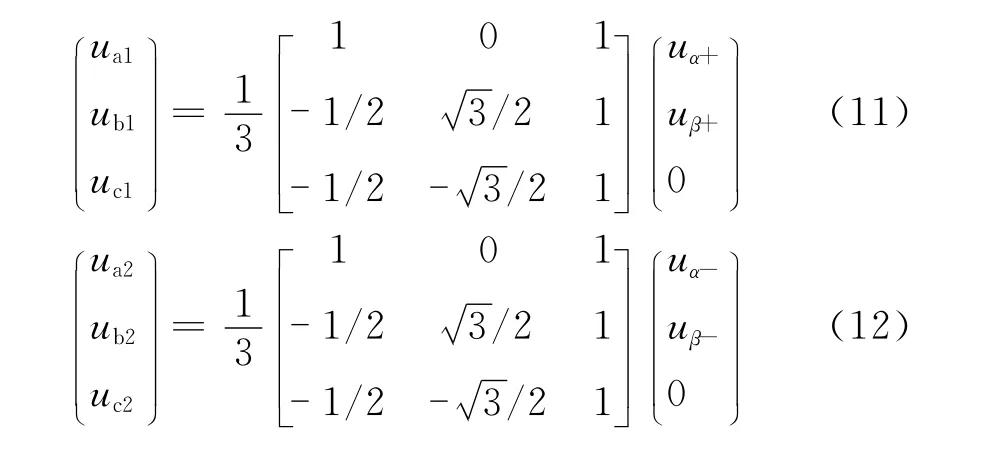
用三相瞬时值表示基波正序分量：

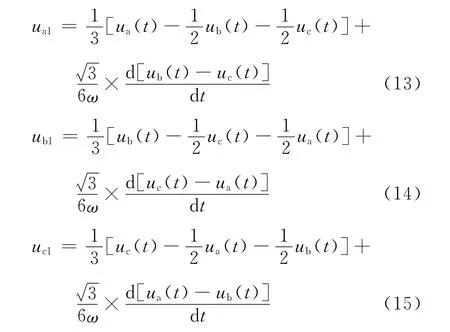
用三相瞬时值表示基波负序分量：

在获取了基波分量的基础上，应用瞬时无功理论可以实时性进行正、负、零序变换计算出系统无功和有功功率。图2示出了正序无功和有功计算原理图，同样方法也适用于负序。

图2 正序有功功率与无功功率的计算原理图Fig.2 Schematic calculation for active power and reactive power of positive sequence component

2 基于瞬时对称分量法的无功补偿

以电弧炉系统的无功功率为控制对象，可以减少电弧炉系统的无功波动以及对系统电压的影响。以控制无功功率稳定为目标，采用滞环电流控制方法实现无功补偿。

电弧炉无功补偿控制系统结构如图3所示，由6个绝缘栅双极型晶体管IGBT（insulated gate bipolar transistor）构成的逆变电路组成工作主体。直流侧并接电容C，交流侧通过3个电感L与电网相连交流侧电抗器，滞环电流控制模块与补偿电流计算模块构成控制电路。

图3 电弧炉无功补偿控制系统结构Fig.3 Control system of reactive power compensation in the EAF

基于瞬时对称分量法的补偿电流计算原理如图4所示。

图4 补偿电流的计算原理图Fig.4 Schematic calculation of compensation current

图中i1和u1是电力系统的三相电流及电压，i′1和u′1是采用瞬时对称分量法公式（13）～ （15）计算的基波正序电流及电压，i′2和u′2是采用瞬时对称分量法公式（16）～（18）计算的基波负序电流及电压，q1和q2是基波正序及负序无功功率，iq1和iq2是基波正序及负序无功电流，i0是基波无功电流，作为补偿电流的参考值，所以用这种方法只能补偿无功的基波分量。

3 系统无功补偿的MATLAB仿真

以40t电弧炉为例，通过MATLAB仿真证明所提出方法的有效性。

3.1 仿真模型

电弧炉无功补偿系统的仿真模型如图5所示。仿真模型由三相电压源模型，三相谐波滤波器模型，补偿电流计算模型，电弧炉用变压器模型，电弧炉的仿真模型和滞环电流控制仿真模型组成。

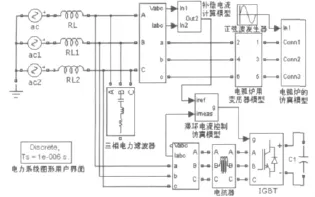
图5 系统的MATLAB仿真模型Fig.5 Simulation model of the system by using MATLAB

补偿电流计算模型如图6所示。

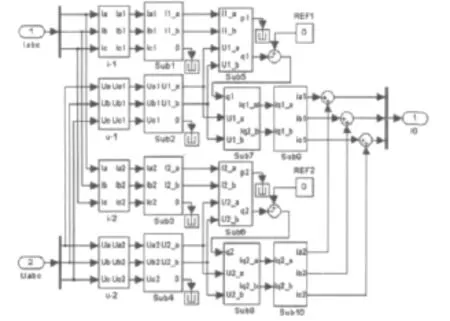
图6 补偿电流计算的仿真模型Fig.6 Simulation model of compensation current calculation

图中REF1，REF2是无功补偿的正序和负序分量参考值，一般负序分量参考值为零，正序分量参考值按电力系统的短路容量或电弧炉运行特性选择。

电弧炉用变压器模型包括短网电路模型。电弧炉的仿真模型当电弧炉工作于熔化期时可以采用参考文献［9］提出的电弧模型，如图7所示。

为了模拟电弧炉引起的电压波动与闪变，采用将正弦波发生器直接叠加于确定性电弧电压上的建模方法。由于人的视觉系统对频率为8.8Hz的电压波动最为敏感，选择的正弦波频率范围为8～10Hz。

滞环电流控制仿真模型如图8所示。

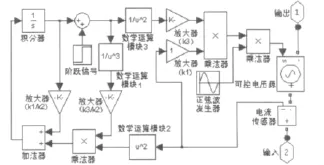
图7 单相电弧炉的仿真模型Fig.7 Simulation model of single－phase electric arc furnace

图8 滞环电流控制仿真模型Fig.8 Simulation model of hysteresis current control

3.2 仿真结果

首先利用瞬时对称分量法求补偿电流，这里假设系统电流和电压的瞬时值分别为

其中，ω表示系统角频率ω＝100π。

为了研究动态情况，假设a相电流幅值和电压幅值在过0.04s时被系统干扰突变为0.8，采用图5模型求出的无功补偿电流波形如图9所示，此时设定正序无功功率参考值为－1.44，负序无功功率参考值为0。

图9 补偿电流的合成波形Fig.9 Synthetic waveform of compensation current

从仿真波形可知，补偿电流响应速度很快，不到1／4周期的时间内即做出了响应。

其次对电弧炉系统无功补偿进行仿真，40t电弧炉变压器与短网的电气参数见表1。

表1 电弧炉变压器与短网的电气参数Tab.1 Electrical parameters of the electric arc furnace transformer and short network

无功补偿前电弧炉系统的单相电压和电流的波形在任何期间内如图10所示。

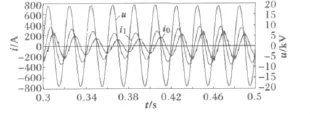
图10 补偿前电压与电流波形Fig.10 Voltage and current waveform before compensation

图中u为系统电压波形，i0为补偿电流计算波形，i1为电弧电流波形（无功补偿前电弧电流等于系统电流）。从波形可知，电压波动和电压与电流的相位差变化很明显，即功率因数cosφ为0.7～0.8，补偿电流计算波形畸变，因为电流或电压的正序与负序分量计算时，微分环节的突变作用存在。为避免突变作用，将时间常数T＝0.001 5s的一阶惯性环节模型加进图6的输入口。一阶惯性环节模型是对输入信号的滤波作用，如图11所示。

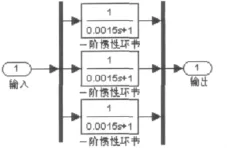
图11 一阶惯性环节模型Fig.11 One－order inertia model

输入信号滤波后电压电流波形如图12所示。

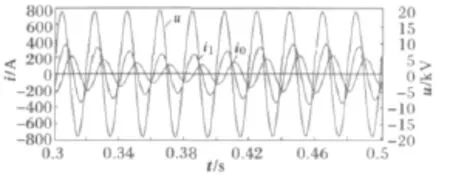
图12 输入信号滤波后电压与电流波形Fig.12 Voltage and current waveforms after filtering the input signal

无功补偿后系统的电压与电流波形在任何期间内如图13所示，正序与负序无功功率参考值分别为零。

图13 补偿后电压与电流波形Fig.13 Voltage and current waveform after compensation

图中i为系统电流波形，i0为补偿电流计算波形，i1为电弧电流波形，i2为补偿电流波形。它们存在着：

从仿真波形可知，电压波动改善，能够实时补偿无功功率波动，功率因数cos≈1。

4 结语

无功波动将会引起电网电压的波动造成电压闪烁，因此电弧炉控制系统需要保持无功功率的稳定。与传统的无功补偿相比，文中提出的实时补偿方法计算系统无功功率时没有时间延迟，实时性很好，相对于传统的无功计算方法具有更快的计算速度。然而，当系统电压电流信号含有大量谐波时，将对突变时刻功率获取和补偿效果产生影响，这也是本文将来进一步研究的方向。

［1］ 花辉（Hua Hui）.冶金企业供电系统电压波动的动态补偿（Dynamic compensation of voltage fluctuation metallurgical power supply system）［J］.工 业 加 热（Industrial Heating），1996，25（6）：29－32.

［2］ Fei－feng Ji，Khan M M，Chen Chen.Static Var compensator based on rolling synchronous symmetrical component method for unbalance three－phase sys－tem［C］∥IEEE International Conference on Industrial Technology，Hong Kong，China：2005.

［3］ Zang Z，Fahmi N R，Norris W T.Flicker analysis and methods for electric arc furnace flicker（EAF）mitigation（a survey）［C］∥IEEE Porto Power Tech Proceedings，Porto，Portugal：2001.

［4］ 张玲玉，李丽梅（Zhang Lingyu，Li Limei）.对称分量法在过载保护电路中的应用（Application of the symmetrical components method in the polyphase asymmetrical AC systems）［J］.长沙通信职业技术学院学报（Journal of Changsha Telecommunication and Technology Vocational College），2009，8（1）：62－64.

［5］ 袁旭峰，程时杰，文劲宇（Yuan Xufeng，Cheng Shijie，Wen Jinyu）.改进瞬时对称分量法及其在正负序电量检测中的应用（An improved method of instantaneous symmetrical components and its detection for positive and negative sequence current）［J］.中国电机工程学报（Proceedings of the CSEE），2008，28（1）：52－58.

［6］ 姜齐荣，谢小荣，陈建业.电力系统并联补偿：结构、原理、控制与应用［M］.北京：机械工业出版社，2004.

［7］ 薛定宇，陈阳泉.基于MATLAB的系统仿真技术与应用［M］.北京：清华大学出版社，2006.

［8］ 李鑫（Li Xin）.基于瞬时无功理论的SVC控制方法的研究（Study of SVC Control Schema Based on the Instantaneous Reactive Power Theory）［D］.西安：西安理工大学自动化与信息工程学院（Xi＇an：School of Automation and Information Engineering of Xi＇an U－niversity of Technology），2006.

［9］ 王育飞，潘艳霞，姜建国（Wang Yufei，Pan Yanxia，Jiang Jianguo）.基于MATLAB的交流电弧炉随机模型与仿真 （Stochastic model of AC electric arc fur－nace based on MATLAB）［J］.高电压技术（High Voltage Engineering），2008，34（5）：973－977.

［10］ 张晓滨，王小艳，钟彦儒，等（Zhang Xiaobin，Wang Xiaoyan，Zhong Yanru，et al）.基于静止无功发生器的三态滞环控制策略研究（Three level hysteresis current control method based on static var generator）［J］.电子技术应用（Application of Electronic Technique），2010，36（6）：84－87.

［11］ 张 竹，张 代 润，王 超，等 （Zhang Zhu，Zhang Dairun，Wang Chao，et al）.有源电力滤波器定频滞环电流控制新策略（Novel hysteresis current control method for active power filter with constant switching frequency）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2010，22（2）：82－85.

［12］ 郑征，杜翠静，常万仓（Zheng Zheng，Du Cuijing，Chang Wancang）.三相不对称系统中谐波电流检测的新方法（New method of harmonic current detection for unbalanced three－phase power system）［J］.电力系统及其自动化学报（Proceedings of the CSUEPSA），2010，22（3）：50－54.