电网混沌系统的T－S模糊非线性PI控制

李向群，刘 浩，罗诗敏，杨龙月，翟周林

（1.中国矿业大学计算机学院，徐州221116；2.中国矿业大学信电学院，徐州221116）

现代电力系统作为一个强非线性、高耦合性和不可避免的不确定性的复杂系统，存在复杂的分岔及混沌运行行为［1～3］，表现为铁磁谐振、混沌振荡以及电压崩溃等现象。这种混沌运行会造成系统过电压，引起过电流，长时间的持续振荡将造成绝缘闪络、避雷管爆炸、设备损坏，严重时会造成停电事故。

目前，国内外学者对于混沌现象的控制已提出了较多方法［4］，如延迟反馈法、自适应控制、智能控制等。在电力系统混沌控制方面，很多先进的控制理论、方法和技术也被引入，用以提高电网安全稳定，主要的方法是向电力系统注入有功和无功能量，通过控制能量的注入，将系统从混沌状态引导至正常运行状态［7］。这些方法的提出和应用为系统的安全运行提供了可靠的保证。但是由于不同电网结构复杂性和操作形式不同，不同的电网控制时采取的控制策略与手段也不同。基于电网的特殊性和所连接设备的属性，对电网建模并对其混沌控制技术进行研究，有助于消除或延迟非线性振荡现象，提高电网的稳定性，同时也可以为基于柔性输配电技术及发电控制系统的混沌控制设计提供理论指导和技术支持，对安全生产具有重要意义。

本文根据电网混沌模型的强非线性和局部线性特性，提出一种电网T－S模型非线性状态PI控制的方法。建立相应的T－S模糊模型，将强非线性系统局部线性化，使其在一定精度上逼近原系统模型，根据并行补偿原理，设计非线性状态PI控制器，进一步克服系统的非线性。应用模糊系统的控制理论求得模糊控制器，用此非线性控制器对电网混沌模型进行控制，由仿真分析验证了该方法的有效性和准确性。

1 电网的非线性动力学分析

本文主要考虑系统的外在因素（如扰动对系统）的影响，而暂不考虑网侧等值系统各端转动惯量等内在因素，建立高压电网可等效图，如图1所示。

图1 电网等效系统图Fig.1 Equivalent system of power grid

给出电磁功率扰动情况下的电网混沌二阶模型［8］：

其中：σ（t）＝σ1－σ2为系统1、2等值发电机q轴电势间相对角度，rad；ω（t）为相对角速度，rad／s；H为等值转动惯量，kg·m2；D等值阻尼系数，N·m·s／rad；Pmax为系统1输送至系统2电磁功率最大值，W；Pm为等值发电机1的机械功率，W；Pξ为扰动功率幅值，W；β为扰动功率的频率，Hz。δ＝ΔpPmax为电磁功率扰动幅值，Δp为电磁功率增大倍数。此时系统中存在2个扰动项，Pξ和δ分别为2个扰动幅值。

为了直观表现系统运动状态［10］，取k＝0.8 Hz，Pξ＝2W，Pmax＝100W，H＝100kg·m2，Pm＝20W，D＝40N·m·s／rad，β＝1Hz，｛σ，ω｝变量的初值｛π／15，0｝。

分析得到电磁功率扰动δ变化时的电网运行状态：

当δ＝0时，系统正常工作；

当0＜δ＜127时，随着扰动幅值的增加，其运行轨道出现了周期4、周期8、周期16的倍周期分岔状态；

当δ≥127时，系统工作在混沌状态。

下面给出δ＝127时的σ－ω相图，σ时序图，ω时序图如图2所示。

图2 混沌运行状态Fig.2 Chaotic running state

2 电网混沌控制器设计

2.1 电网T－S模型

T－S模糊模型是将非线性系统用一组“如果－则”模糊规则来描述，其中的每一条模糊规则代表一个子系统。整个模糊系统由各个子系统的线性组合构成。模糊规则状态方程模型可以表示为

其中：Ri为模糊系统第i条规则，x＝ ［x1，x2，…，xp（t）］T表示模糊系统状态向量，（i＝1，…，l，k＝1，…，n）表示系统的模糊集合。

利用单点模糊法模糊化，模糊推理采用Sum－Product推理，采用重心法解模糊，最终得到的模糊系统总体模型表示为

如图2所示，当电网系统运行在混沌状态时，功角σ的变化范围为－2＜σ＜3，因此，系统模型的不确定项sinσ的取值范围－1＜sinσ＜1，给出不确定项的模糊近似如表1。

表1 不确定项模糊近似表Tab.1 Fuzzy approximate table of uncertainties

其中σ1＝－2／π，σ2＝0，σ3＝2／π，Δσ＝2／π，参考表1，本文用三个子系统去近似逼近原系统，给出模糊规则：

选取隶属度曲线：

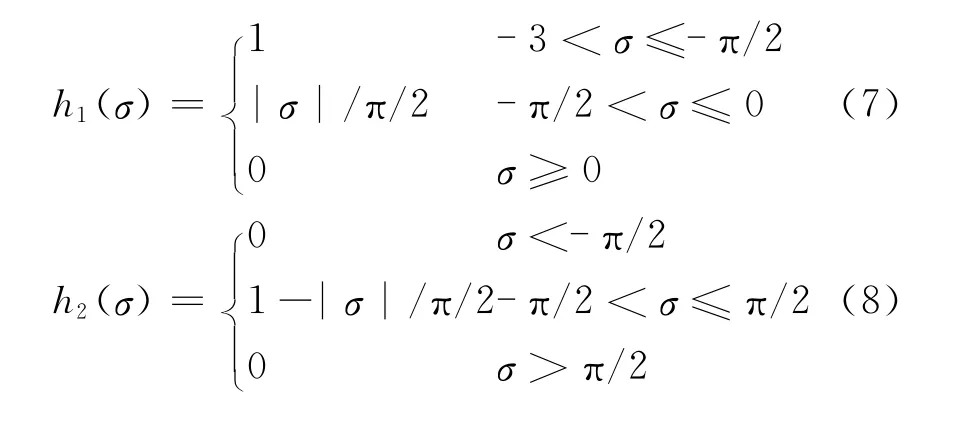
用h1、h2、h3分别表示三个子系统的隶属度，最终系统的模糊模型可表示为

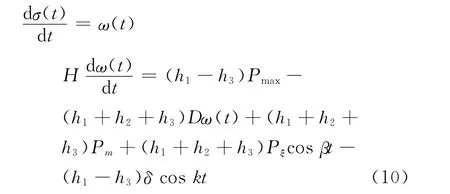
隶属度曲线如图3所示。

图3 T－S模型隶属度函数Fig.3 Membership function of T－S model

2.2 非线性状态PI控制器

为实现电磁功率扰动下电网的混沌控制，维持功角σ恒定，并使角速度ω稳定到0，对电网T－S模型的3个子系统分别设计了非线性PI控制器，该控制器既具有线性PI控制器的良好控制能力，又能克服系统被控对象变化的干扰。以状态变量ω作为控制量，设计非线性PI控制器形如：

其中，i＝1，2，3。eω（t）＝ωst－ω（t）为状态量与给定值的实时偏差，ωst为给定值，kp为比例增益参数，ki为积分增益参数。

（1）比例增益参数kp

在响应初始阶段，比例增益参数kp应取较大值以实现系统的快速响应，同时为抑制过大超调，kp应随输出y的增大而减小；当系统出现超调时，为了加强反向控制作用以实现快速“制动”，kp应逐渐增大；在系统偏差较小时，为了使输出尽快稳定到指定点，应抑制较大的kp带来的惯性，期望kp较小。构造如下非线性函数：

kp取值空间为［ap，ap＋bp］，当误差ey（t）→±∞ 时，kp取最大值；当ey（t）＝0时，kp取最小值。cp是kp的非线性系数，调节cp的大小可以调节kp的变化速率。

（2）积分增益参数ki

偏差较大时，积分增益不宜太大，否则可能会引起震荡；而当偏差较小时，积分增益取值应适当增大，使其快速抑制系统输出偏差。积分参数非线性函数可以表示为：

电网T－S模型的3个模糊子系统滑模变结构控制器分别为u1，u2，u3，由已知的隶属度曲线设计总系统控制器，可得控制器的形式如下：

2.3 非线性状态PI控制稳定性分析

下面通过系统的稳定性分析来确定PI参数的范围。

基于电网T－S模糊模型，为确保消除系统混沌，加入PI控制器后，在平衡点P（π／15，0）处线性化系统方程。

得到系统的Jacobian矩阵为

得出对应的特征方程

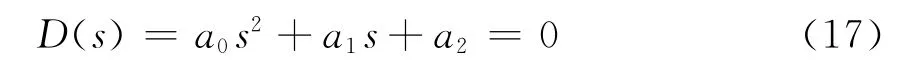
其中：a0＝1

闭环系统渐近稳定的条件为雅克比矩阵的两个特征值的实部均为负。为降低控制成本适当限制kp、ki的范围，限定kp＜100且ki＜100，得出kp、ki取如下范围时系统稳定，kp＞－40，ki＞－223。

又因闭环系统应为负反馈系统，故当取值kp＞0，ki＞0时，系统稳定。

分析知，所设计的非线性PI控制器中，ap、bp决定kp的变化范围，cp决定kp的非线性变化；ai、bi决定ki的变化范围，ci决定ki的非线性变化。

考虑到控制成本，限定ap＜1，bp＜4，ai＜1，bi＜4，cp＜10，ci＜10，即kp＜5，ki＜5。

当σ→－π／2时，取非线性参数向量为［0.70，3.77，4.02，0.67，2.70，0.08］；

当σ→0时，参数向量为［0.61，3.47，8.08，0.22，2.69，0.60］；

当σ→π／2时，参数向量为［0.46，3.53，9.61，0.88，3.90，1.82］。

3 电网混沌控制仿真研究

采用上述控制参数对电网混沌二阶模型进行控制仿真研究，在第10s投入控制，控制效果如图4所示。

图4 电网T－S模型控制效果Fig.4 Control result of T－S model of power grid

在第10s加入非线性PI状态控制器后，系统很快的趋向平衡点，可见在功角ω项上加PI控制器就能快速抑制混沌，并使系统达到平衡态。

本文定义一个稳态误差标准以观测控制系统是否实现了稳态无静差。数值仿真中取积分步长为0.001s，对控制过程中150s～200s内的50000个点取方均根误差，得到上述非线性PI控制的稳态误差为4.4902×10－4。这说明，对电网 T－S模糊模型设计的非线性PI状态控制器可以对系统精确模型进行有效控制，很好地实现无静差控制。

4 结论

本文研究了基于T－S模糊模型的电网混沌行为非线性PI状态控制研究，可得以下结论：

（1）构造了电网T－S模糊模型，将系统划分为三个子系统，并确定了相应的基于功角的隶属度函数；

（2）利用平行分布补偿法，从快反应速度、低超调、小惯性等目标出发构造了状态非线性PI控制器；

（3）根据非线性状态PI控制器参数整定，优化控制器参数，实现了稳态无静差的控制要求，动态控制效果较好。

［1］ 卢强，梅生伟，孙元章.电力系统非线性控制（第二版）［M］.北京：清华大学出版社，2008.

［2］ 薛禹胜，周海强，顾晓荣（Xue Yusheng，Zhou Haiqiang，Gu Xiaorong）.电力系统分岔与混沌研究述评（A review of bifurcation and chaos researches in power systems）［J］.电力系统自动化（Automation of Electric Power Systems），2002，26（16）：9－15.

［3］ 刘凡，孙才新，司马文霞，等（Liu Fan，Sun Caixin，Sima Wenxia，et al）.铁磁谐振过电压混沌振荡的理论研究（Theoretical analysis of chaotic oscillation of ferroresonance overvoltage in power systems）［J］.电工技术学报（Transactions of China Electrotechnical Society），2006，21（2）：103－107.

［4］ 李卫东，王秀岩（Li Weidong，Wang Xiuyan）.混沌控制综述（A survey of chaotic control）［J］.自动化技术与 应 用 （Techniques of Automation and Applications），2009，28（1）：1－5，9.

［5］ Lu Zhao，Shieh Leang－San，Chen Guanrong，et al.Adaptive feedback linearization control of chaotic systems via recurrent high－order neural networks［J］.Information Sciences，2006，176（16）：2337－2354.

［6］ Pyragas K.Control of chaos via extended delay feedback［J］.Physics Letters A，1995，206（5－6）：323－330.

［7］ Liu Chih－Wen，Thorp James S，Lu Jin，et al.Detection of transiently chaotic swings in power systems u－sing real－time phasor measurements［J］.IEEE Trans on Power Systems，1994，9（3）：1285－1292.

［8］ 张强（Zhang Qiang）.电力系统非线性振荡研究（Study on nonlinear oscillations of electric power system）［J］.电力自动化设备（Electric Power Automation Equipment），2002，22（5）：17－19.

［9］ 代姚，司马文霞，孙才新，等（Dai Yao，Sima Wenxia，Sun Caixin，et al）.应用T－S模糊方法对铁磁谐振过电压的混沌抑制（Chaos controlling in ferroresonance overvoltage with T－S fuzzy method）［J］.高电压技术（High Voltage Engineering），2010，36（4）：878－883.

［10］ 宋运忠，赵光宙，齐冬莲（Song Yunzhong，Zhao Guangzhou，Qi Donglian）.电力系统混沌振荡的自适应补偿控制（Adaptive compensation control for chaos oscillation of power system）［J］.电力系统及其自 动 化 学 报 （Proceedings of the CSU－EPSA），2006，18（4）：5－8，81.

［11］ 张智晟，马龙，孙雅明（Zhang Zhisheng，Ma Long，Sun Yaming）.混沌理论和支持向量机结合的负荷预测模型（Load forecasting model using chaos theory and support vector machine）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2008，20（6）：31－35.