基于Gompertz曲线和三次指数平滑法的货运量组合预测
2012-07-02印凡成王滕滕黄健元
印凡成 ,王滕滕 ,黄健元
(1.河海大学 理学院,江苏 南京 210098;2.河海大学 公共管理学院,江苏 南京 210098)*
0 引言
货运量预测是水路网规划的重要内容,是评价水运交通现状、分析建设项目必要性和可行性的基础,货运量预测水平将直接影响项目决策和水路网规划方案的科学性和合理性.因此准确地对货运量进行预测,并根据其变化趋势采取相应措施,是水运系统持续健康发展的有效保障.货运量预测常用的方法有:回归分析法、灰色预测法、三次指数平滑法等[1-2],每种方法使用条件不尽相同,预测结果及精度也有差异.由于系统的复杂性,很多情况下利用单一方法进行预测往往具有片面性,组合预测方法就能发挥很好的作用[3-4].自Bates和Granger于1969年首次提出组合预测理论以来,组合预测已成为预测领域的一个重要研究方向[5].
通过到苏北航道处现场访谈,根据京杭运河苏北段调查资料和江苏省经济发展信息,结合水运系统自身成长规律,利用 Gompertz曲线拟合[6-7]和三次指数平滑[8-9]两种模型相互验证及组合预测,结合专家意见得出最终预测值,力求预测结果同实际情况相符合,为相关部门的决策提供科学依据.
1 预测方法
1.1 Gompertz曲线拟合法
Gompertz曲线拟合法[6-7]预测模型为:
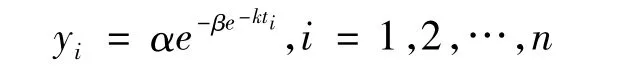
式中,yi为历年数据中第i年的货运量;ti为不含误差的确定性时间变量,此处即为历年数据中从基期开始的第i年;α、β、k为待标定参数,其中α为y的极限参数,Gompertz曲线参数α、β、k的标定,通常采用非线性最小二乘法估计参数,使

1.2 三次指数平滑法
三次指数平滑法[8-9]预测模型为:

式中,Yt+T为时刻t+T的预测值;


1.3 组合预测法
组合预测[3-4]具体方法为:设预测问题在某一时段的实际值为yt(t=1,2,…,n),对此问题有m种可行的单项预测方法,其预测值或模型的拟合值分别为:fit(i=1,2,…,m;t=1,2,…,n)

本研究采用“组合预测误差平方和最小”作为组合预测的最优准则,建立组合预测模型:

式中,f(t)为t时刻组合预测模型的预测值;f1(t)为t时刻第一个模型的预测值(Gompertz曲线拟合法的预测值);f2(t)为t时刻第二个模型的预测值(三次指数平滑法的预测值);a1、a2分别为第一、第二个模型的权重且a1+a2=1;ai≥0,(i=1,2);
设 t时刻的实际值为Y(t),t=1,2,…,M,则组合预测误差平方和为:
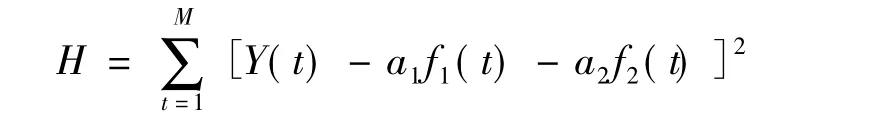

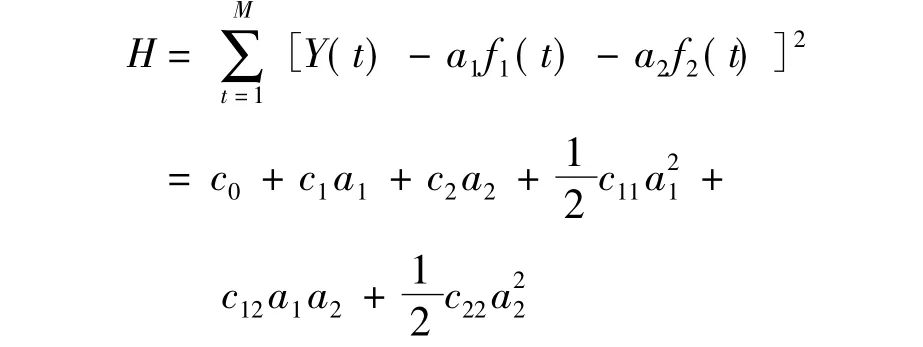
以组合预测误差平方和H为最小目标,则有如下非线性规划模型:

2 实例分析
2.1 京杭运河苏北段货运量单项预测模型
通过对京杭运河苏北段历年货运量[10](见表1)采用Gompertz曲线进行拟合:

表1 京杭运河苏北段船闸历年货运量情况
可得未来发展年货运量的预测公式:
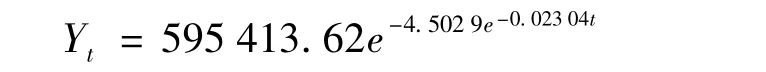
式中,Yt为t期苏北段货运量预测值;t为时期数;设1999年为基年,对应的时期数t=0.
运用上述公式预测苏北段未来发展水平年货运量,并考虑10年水利改革发展四万亿投资的拉动、2020年投资结束后续影响,2025年后货运量增长率的降低以及以后年份的增幅趋缓等因素,可确定预测初值,如表2.
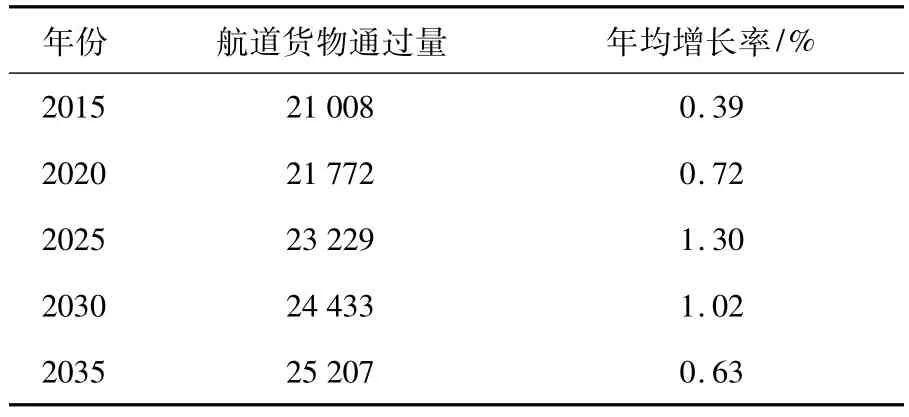
表2 京杭运河苏北段货运量预测初值(一)万吨
通过对苏北段历年货物运量序列进行三次指数平滑可得到未来发展趋势的预测值,预测公式:
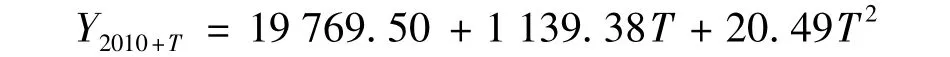
T为基础年份(2010)至预测年份年数,代入上式可求得发展水平年苏北段货运量,再考虑水利改革发展的影响,可确定预测初值,如表3.
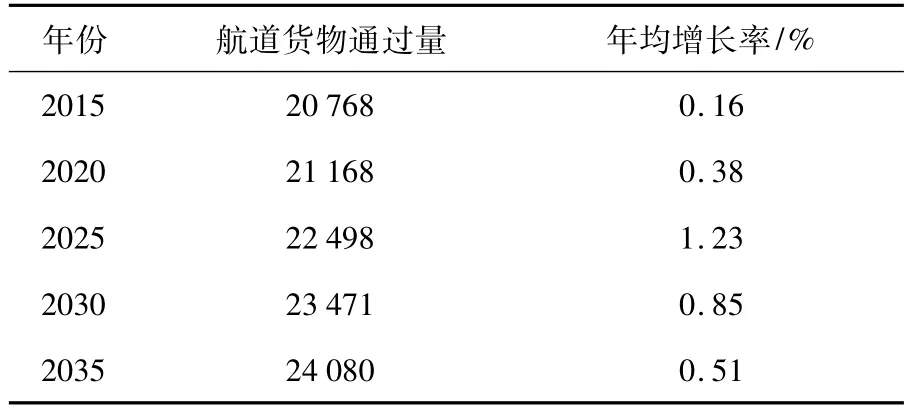
表3 京杭运河苏北段货运量预测初值(二)万吨
2.2 京杭运河苏北段货运量组合预测模型建立组合预测模型:
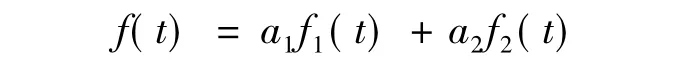
式中,f(t)为t时刻组合预测模型的预测值;f1(t)为t时刻第一个模型的预测值(Gompertz曲线拟合法的预测值);f2(t)为t时刻第二个模型的预测值(三次指数平滑法的预测值);a1、a2分别为第1、第2个模型的权重且a1+a2=1;ai≥0,(i=1,2);
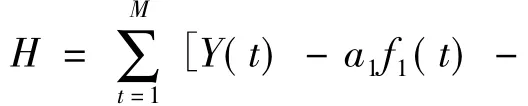
通过组合预测模型进行预测,综合考虑各种影响因素,结合专家咨询意见,将定量计算与定性分析有机地结合起来,经过综合分析评价将货运量预测值进行合理的调整,得到京杭运河苏北段货运量预测初值,见表4.
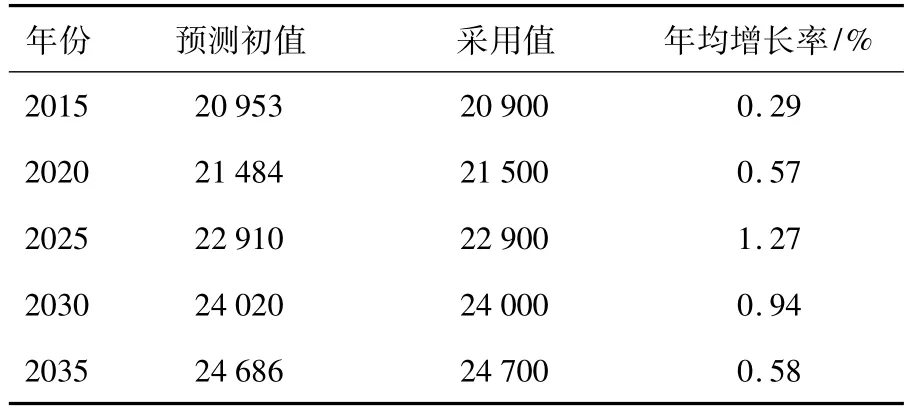
表4 京杭运河苏北段货运量预测初值 万吨
3 结论
准确合理地进行货运量预测,对确定水利交通设施的建设规模、制定未来运输发展战略有重要的影响.本文以京杭运河苏北段为例,引用最优加权组合建模理论,采用Gompertz曲线拟合法和三次指数平滑法建立组合预测模型,以预测误差的平方和最小为目标函数来确定权重系数,再结合专家咨询意见,综合分析最终确定货运量预测值.该组合预测模型精度能很好地满足预测需求,达到满意的预测效果,预测结果更贴近实际,具有较强的实用性,可应用于国家、城市及地区的货运量预测,具有一定的理论价值和现实意义.在此基础上对水运系统货物运量的细化分析还有待进一步研究.
[1]王毅成,林根祥.市场预测与决策[M].湖北:武汉工业大学出版社,1998.
[2]王振龙.时间序列分析[M].北京:中国统计出版社,2000.
[3]杨鹏程,龙建成,马建军.铁路货运量的组合预测方法研究[J].物流科技,2006,29(11):66-68.
[4]赵明华,龙照,邹新军.基于Logistic曲线和Gompertz曲线的最优组合沉降预测模型及其应用[J].公路交通科技,2007,24(12):1-4.
[5]文军,蒋由辉,方文清.航空货运量得优化组合预测模型[J].计算机工程与应用,2010,46(15):215-217.
[6]GOMPERTZ B.On the Function Expressive of the Law of Human Mortality,and on a new Method of Determining the Value of Life Contingencies[J].Philosophical Transactions of the Royal Society of London.Series A,Mathematical and Physical Sciences,1825,34:513-585.
[7]余闯,刘松玉.路堤沉降预测的Gompertz模型应用研究[J].东南大学学报,2005,126(1):82-86.
[8]阎善郁,李丰岩,荣文竽.三次指数平滑法预测大连港货物吞吐量[J].大连交通大学学报,2009,30(2):44-47.
[9]程雪平,林国龙.基于三次指数平滑法的集装箱吞吐量预测[J].网络安全技术与应用,2010(5):59-61.
[10]国家统计局.江苏统计年鉴[M].江苏:中国统计出版社,1999-2010.
