基于NSGA-II的宽带天线匹配网络设计
2012-07-02宋智李焱淼许丽群朱义胜
宋智,李焱淼,许丽群,朱义胜
(1.大连海事大学 信息科学技术学院,辽宁 大连116026;2.大连交通大学 电气信息学院,辽宁 大连116028;3.大连交通大学 理学院,辽宁 大连 116028)*
0 引言
现代天线匹配网络的优化设计问题一直受到人们的广泛重视.Carlin提出实频法[1],Pandel和Fettweis提出参数计量法[2]和直接法.随着人工智能技术的发展,遗传算法[3]、模拟退火算法[4]、改进的高斯牛顿法[5]等都在天线匹配网络的设计中取得了一定成果,其中经常遇到多目标函数的优化问题.但上面提到的多目标优化方法主要是将多目标优化问题转变为单目标优化问题.采用单目标优化的方法求解,每次只能得到一个解,需经过多次运算后才能得到一组近似Pareto最优解,而且因为每次计算结果彼此独立,可能出现结果不一致的情况.加权的目标函数之间通过决策变量相互制约,最终优化目标仅为各个目标之和,各个目标的优化进度不可操作.
多目标遗传算法用来解决多目标优化问题,其核心是协调各个目标函数之间的关系,找出使各目标函数能尽量达到比较小(或比较大)的Pareto最优解集.在众多的多目标遗传算法中,影响较大的是 NSGA-II算法[6].本文将 NSGA-II算法应用于频率范围为10~590 MHz的宽带天线匹配网络的设计.仿真结果表明,利用NSGA-II算法优化得到宽带匹配网络具有随天线阻抗变化灵敏度低的特点,能兼顾系统的驻波比和效率,该算法适用于各种宽带天线匹配网络的优化设计.
1 宽带天线匹配网络
图1所示二端口网络为待设计的天线匹配网络,ZL表示匹配网络所接天线的阻抗.

图1 二口网络端
图1中二端口网络散射矩阵为[7].

输入端口反射系数为
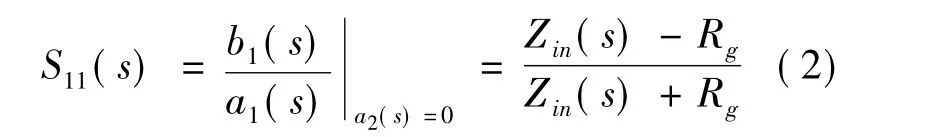
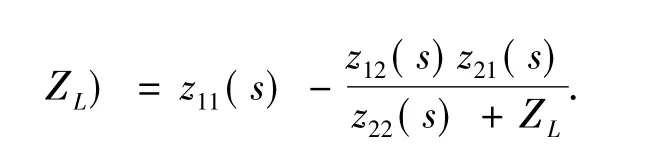
网络的传输功率增益[8]

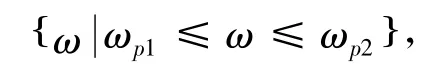

式中,Ωp为通带的截止频率区间;σp是小的正数.
2 NSGA-II算法
多目标优化问题(Multi-Objective Problem,MOP)一般由n个决策变量参数、k个目标函数和m个约束条件组成,目标函数、约束条件与决策变量之间是函数关系.最优化目标函数如下[9]:

其中,x=(x1,x2,…,xn)∈ Χ ,y=(y1,y2,…,yn)∈Υ,x表示决策向量,y表示目标向量,Χ表示决策向量x形成的决策空间,Υ表示目标向量y形成的目标空间,约束条件e(x)≤0确定决策向量的可行取值范围.
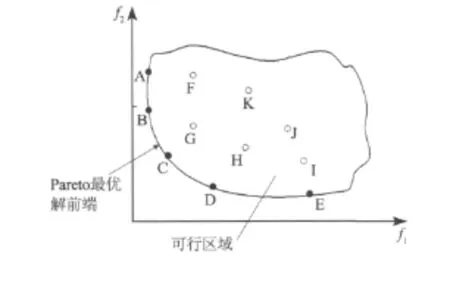
图2 两个目标的Pareto前端分布
多目标优化问题的解是一组,即所说的Pareto最优解集.图2中实心点A、B、C、D、E均处在最优边界上,都是最优解,是非支配(Non-dominated)的;空心点 F、G、H、I、J、K 落在搜索区域内,但不在最优边界上,不是最优解,是被支配(Dominated)的,这些点直接或间接地受最优边界上最优解的支配,是劣于最优前端上的最优解.
非劣排序遗传算法(NSGA)是Srinivas和Deb于20世纪90年代初期提出,它是基于Pareto最优概念的多目标遗传算法.Deb于2002年在NSGA的基础上进行了改进,提出了一种精英保留非劣排序遗传算法(NSGA-II),定义了拥挤距离,通过估计某个点周围的解密度取代适应值共享.
本文将NSGA-II算法引入宽带天线匹配网络的设计中,其步骤为[10]:
(1)初始种群产生.根据具体问题的取值和限制进行随机初始化一个父种群,网络中元件产生为f(i)=min+(max-min)*rand(1).
(2)快速非支配排序.根据个体的非劣解值对种群进行分层,首先找出种群中所有非支配的个体,保存在当前集合中,赋予它们一个共享的虚拟适应度值,当前集合中的个体为第一个非支配层的个体.然后忽略这组被分层的个体集合,对种群中的其余个体继续重复以上过程,直到种群中的所有个体都被分层.
(3)拥挤度计算和比较准则.按照多目标匹配网络的数学模型计算每个个体对应的目标函数值,再根据目标函数值进行非劣分层,计算每层个体的拥挤距离值.如果两个个体具有不同的非劣级别,进行比较后,选择级别低的个体;如果两个个体具有相同的非劣级别,选择具有较大矩形体的个体.
(4)交叉和变异.NSGA-II算法对实数编码,采用模拟二进制交叉(SBX)和多项式变异.SBX算子模拟二进制交叉算子的过程,对实数编码的父代个体进行交叉操作.变异算子是基于多项式的变异操作.
(5)精英策略.保留父代中的优良个体使其直接进入子代.
在优化中,为了更好兼顾天线效率,选取输入端口反射系数和传输功率增益作为目标函数.所求目标函数的最优解就是在通带内,实现‖GT‖-∞达到最大值,同时‖S11‖∞有最小值;阻带内正好相反,求出二端口网络中的元件值.算法中的目标函数为
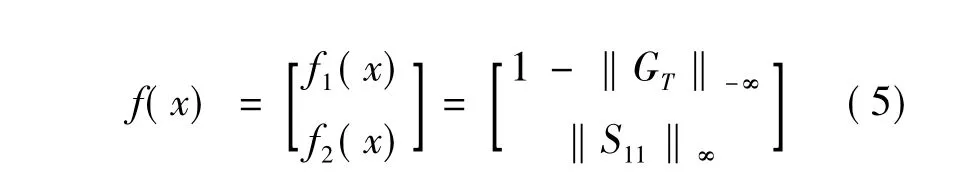
3 仿真实例
用HP8753D矢量网络分析仪测量某天线(10~590 MHz,Rg=50 Ω)的实测输入阻抗如图3所示.在10~590 MHz范围内,按文献[11]采用的如图4所示的网络作为优化设计的宽带天线匹配网络.
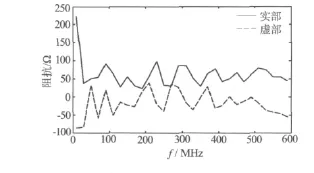
图3 天线输入阻抗

图4 匹配网络结构

附表 匹配网络元件参数
设置 NSGA-II算法参数:最大遗传代数1000,种群个体数目120,交叉算子20,变异算子20.变量为匹配电路中 C1,C2,L1,L2,L3和有耗电阻R1,R2.应用算法得到匹配网络的Pareto最优前端如图5所示,选取其中一组Pareto最优解和文献[11]采用遗传算法优化得到网络的元件值如附表所示.

图5 Pareto最优前端
天线驻波比(VSWR)如图6所示,由图6可知,当天线不加匹配网络时,在10~40 MHz内其驻波比大于3,不满足通信系统的要求.文献[11]加载遗传算法得到的匹配网络后,在整个频带内其驻波比均小于3(平均值小于2.5).加载 NSGA-II算法得到的匹配网络后,其驻波比在1.25~2之间变化,波动范围小于文献值,说明NSGAII算法优化后的匹配网络对天线阻抗变化不敏感,能使天线在10~590 MHz宽带范围内具有良好的宽带性能.
加载匹配网络后系统的传输功率增益变化曲线如图7所示.匹配网络中有耗电阻的引入必定影响整个天线的增益,从图7可以看出,文献[11]遗传算法得到的匹配网络以天线驻波比为主要考虑目标,天线效率达到40%以上.而在NSGA-II算法中兼顾了天线的驻波比和效率,使得在整个频带内,天线效率基本都达到50%以上,天线的效率在对应频率都高于遗传算法.说明应用NSGA-II算法所设计的匹配网络具有更好的性能.

图6 天线驻波比

图7 加载匹配网络后天线效率
4 结论
本文将NSGA-II算法应用于实际天线匹配网络的优化设计,以网络输入端口反射系数和传输功率增益为目标函数设计天线的匹配网络.一次运行得到多个Pareto最优解,选取Pareto最优解,实现了真正意义的多目标优化.仿真结果分析表明,NSGA-II算法优化得到的匹配网络随阻抗变化的灵敏度低,天线系统的效率较高,验证了该方法的有效性.
[1]CARLIN H J.A new approach to gain bandwidth problems[J].IEEE Transactions on Circuit and Systems,1977,24:170-175.
[2]PANDEL J,FETTEWIS A.Broadband matching using parametric representations[J].IEEE International Symposium on Circuits and Systems,1985,36:143-149.
[3]马国田,梁昌洪.基于遗传算法的宽带匹配网络的优化设计[J].微波学报,2000,16(1):73-77.
[4]孙保华,纪奕才,刘其中.VHF/UHF天线宽带匹配网络的优化设计与实验研究[J].电子学报,2002(6):797-799.
[5]朱义胜,郑紫薇.短波宽带天线匹配网络的设计[J].电子学报,2001(8):1049-1075.
[6] KALYANMOYDEB,AMRITPRATAPT, MEYARIVAN.A fast and elitist multiobjective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[7]Zhu Yi-sheng,Chen Wai-kai.Computer-aided design of communication networks[M].World Scientific Publishing Co.Pte.Ltd,Singapore,2000.
[8]ALAN DAVIS W ,KRISHNA K,AGARWAL.Radio Frequency Circuit Design[M].北京:机械工业出版社,2005.
[9]崔逊学.多目标进化算法及其应用[M].北京:国防工业出版社,2006:4-57.
[10]冯士刚,艾芊.带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用[J].电工技术学报,2007,22(12):146-151.
[11]丁霄,姜兴,李思敏.基于遗传算法的宽带匹配网络设计[J].桂林电子科技大学学报,2006,26(6):438-441.
