多Agent系统协作求解的粒子模型方法
2012-07-02赵旭宝李静董靓瑜
赵旭宝,李静,董靓瑜
(大连交通大学 软件学院,辽宁 大连 116021)*
0 引言
在分布式人工智能中,基于Agent结构提供了柔性和鲁棒性,适合解决动态、不确定和分布式的问题.系统中各Agent个体都是具有自主性的智能体,存在自己的信念、愿望、目标等认知属性和承诺、义务、协作、竞争等社会属性[1-2].系统中各Agent个体通过对自身知识的表示和对问题域的描述,构成分布的、异构的、面向特定问题的Agent求解子系统,完成指定任务的求解.但在多Agent分布式系统中由于每个Agent个体所具有的知识资源和执行能力是有限的,当单个Agent难以独立完成指定任务,或多个Agent一起完成会产生更大的效益时,多个A-gent个体之间就倾向于利用协作机制进行信息的交流、知识的共享来完成任务的协作求解.为了保证多Agent系统协作求解的性能,很多学者在关于多Agent系统协作求解模型建立和协作求解方法方面做了大量研究.文献[3]提出面向共同目标的合作求解策略,重点在于寻求系统的最大效益;文献[4-5]提出基于弹簧网络的多Agent系统协作求解方法,通过自组织动力学策略来实现Agent之间的协调;文献[6-7]提出基于合同网协议的合作求解方法,先协商结盟再规划求解,并通过协商的方式解决冲突.
目前多Agent分布式系统协作求解方法的研究基本上有两种类型:一种类型是Agent个体各自寻求自身最大利益的方法;另一种是Agent个体共同寻求整个系统最大效益的方法.但前者协作求解中没有全局的优化目标,缺乏统一的全局控制策略;后者又难以描述Agent个体自变与自组织现象.同时,这两种类型虽然都涉及到Agent间的协作和交互,但协作交互也仅仅是一些简单的社会交互行为,在问题求解过程中不能及时处理环境和Agent本身的动态变化以及社会交互行为的随机性和并发性的问题.
为此,本文提出了一种多Agent系统协作求解的粒子模型方法.将系统协作求解转换为多粒子共同寻优过程,克服了Agent本身认知属性和社会属性动态变化及随机性和并发性的问题,使得Agent个体在协作求解中既获取自身的最大利益,又促进系统的总体效益.最后,引入了协作程度变化参数,给出了Agent协作求解的需求强度计算公式和系统效益目标函数及优化算法,经过算法迭代计算求得了协作求解的资源分配优化解.仿真结果表明该方法具有很好的收敛性和实用性.
1 求解粒子模型
1.1 求解问题描述
不失一般性,本文以多Agent分布式环境下对问题实施任务资源规划分配的协作求解为背景,讨论多Agent系统协作求解方法与优化算法.设待解决的任务Agent集合和知识与执行能力构成的资源Agent集合分别为 Task={AgentT1,AgentT2,…, AgentTn} 和 Res = {AgentR1,AgentR2,…,AgentRm},且每个子资源AgentRi个体拥有的资源容量为mi.子资源AgentRi个体分配给子任务AgentTk个体的资源量为rik(rik≤mik),供其完成规划的任务.同时子任务AgentTk个体付给子资源AgentRi个体单位资源报酬为pik.设第k个子任务AgentTk对各种子资源Agent需求资源总量为Sk和第k个子任务AgentTk所能支付总的资源报酬代价为Pk.子任务AgentTk在执行任务时使用何种子资源Agent取决于子任务AgentTk对子资源AgentRi的需求强度xik(1≤i≤m,1≤k≤n).xik表示第k个任务需要第i个资源.因此,在多Agent分布协作求解中,任务资源规划目标则为寻找一个优化的任务资源规划分配方案,在各资源用量最下的前提下,取得系统整体收益最大值.
1.2 求解粒子模型
由上述问题分析可知,单个子任务AgentTk对各子资源AgentRi的需求是关于rik,pik,xik的函数,函数表示为Aik=F(rik,pik,xik).所有任务对资源需求可以表示成如下的分配矩阵T_R=[Aik]m×n(1 ≤ i≤ m,1≤ k≤ n).矩阵如下:

在上述分配矩阵中,每个子任务AgentTk(1≤k≤n)在完成任务时,可能对每个资源Agent Ri(1≤i≤m)个体存在需求.也就是说,每个子资源AgentRi个体可能分配给不同的子任务(rikxik≤ mi(∀i=1,2,…,m)).这样当多个子任务同时需要某资源时,就可能产生资源使用的冲突.为此,本文提出了资源协作求解的粒子模型.将每个子资源AgentRi个体视为不可再分的个体,称为粒子,每个子资源粒子每次仅能分配给一个子任务粒子.这样,当多个子任务需要同时使用某子资源时,Agent粒子就会倾向于进行协作求解共同完成多个子任务.或当多个子资源Agent粒子一起完成所规划任务会更有效时,也会倾向协作求解.多Agent粒子之间是否进行协作,取决于协作求解强度xik的值.
1.3 需求强度的计算
在实际应用中,对于任务对资源需求强度的取值,不但要考虑Agent意愿、目标等自身认知属性的变化,更要考虑复杂社会交互行为对协作求解中需求强度的影响.对于群体Agent协作求解过程中所涉及的社会交互行为类型大致可分为两类:
(1)对于子任务 AgentTk,子资源 AgentRi粒子与子资源AgentRj粒子的协作交互行为ρijk;
(2)对于子资源AgentRi,子任务AgentTk粒子与子任务AgentTj粒子之间的协作交互行为ρ'kji.
其中,ρijk的含义为:对于子任务AgentTk,如果资源AgentRi与资源AgentRj具有相同的意愿和目标,且产生交互行为能加速对任务的执行,或产生更多的效益,则将加强任务 AgentTk对资源AgentRi粒子与AgentRj粒子的需求,加强的强度为ρijk.相反则消弱.
同理,ρ'kji的含义为:对于子资源 AgentRi,如果任务AgentTk与任务AgentTj之间产生交互合作行为,能简化任务执行的复杂度,并能节约资源的消耗,则将加强资源AgentRi对任务AgentTk粒子与AgentTj粒子的分配.加强的强度为ρ'kji.相反则消弱.
假定不同类型的交互行为产生的效果具有叠加性.因此,根据上述社会交互行为的分类,在协作求解交互过程中,任务对资源的需求强度可通过式(2)计算取得.
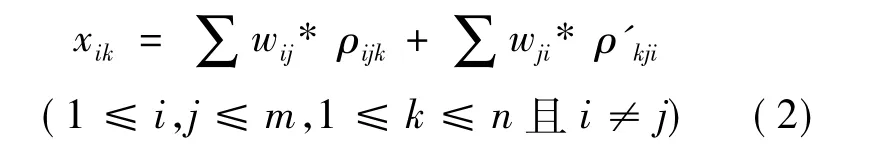
其中,wij为关联权值,在[0,1]之间取值.它表示协作求解中各Agent粒子间关联程度.它随Agent粒子的动态变化而改变.如新陈代谢、随机故障以及协作交互的竞争、利用、欺骗等.在Agent粒子生命周期结束时wij=0.为了简化问题求解的复杂度,本文假定交互行为对需求强度的加强与消弱程度相同,即ρijk和ρ'kji取相同的小数值.
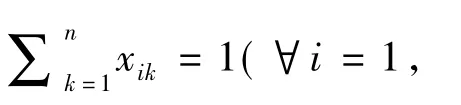
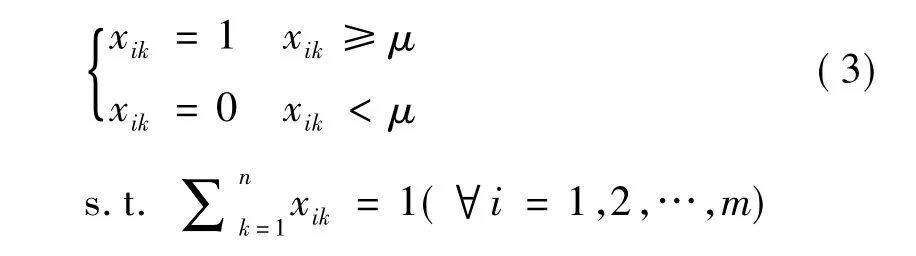
在式(3)中,当计算所得需求强度值超过给定的某阈值μ后,使得xik=1,否则为0.构造后,某次任务资源规划协作求解状态可用图1表示.图1中圆点表示子资源粒子对子任务粒子的分配.有向边表示各粒子之间的协作求解过程.如有向边 <x12,x24>表示子任务粒子T2在使用资源粒子R1时,还需要使用资源粒子R2,但R2已被T4使用.因此资源粒子R1和R2建立协作关系.在图1中有向边越多表明系统内部协作求解规模越大.另外,如果从资源分配角度描述群体Agent粒子间的协作求解交互过程,还可以表示成有向图,如图2.图2中每条边上的权值代表系统消费代价.在协作求解中由于Agent粒子自身的动态变化和社会交互行为随机性、并发性等因素的影响,使得这种协作求解是以通信开销和资源耗费为代价.本文将第i个Agent粒子和第j个Agent粒子协作求解产生的资源消费代价定义为cij.在图2中有向边的多少也体现了系统协作求解交互程度.用变量e∈[0,1]表示系统协作交互程度.

图1 Agent协作求解模型
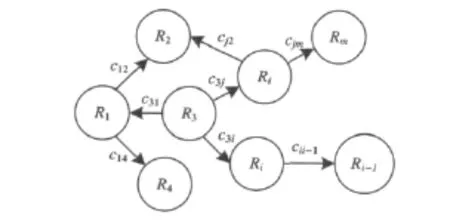
图2 资源Agent协作求解过程
2 求解数学模型
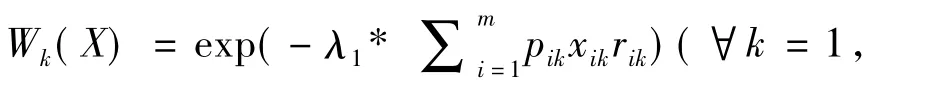

λ1,λ2为(0,1)的随机数
3 协作求解的粒子群算法
在多Agent系统分布式协作求解的粒子模型中,每个规划解xik都是一个0或1值(1≤i≤m,1≤k≤n).显然任务资源协作求解问题属于组合优化问题.因此,本文构造了适合求解的改进粒子群优化算法[8].在每次求解中把子资源数粒子数m定义为算法中每次迭代求解的空间维数.即每一维空间代表一个资源粒子对任务粒子的分配情况,用一个整数来表示.如果某资源粒子在求解中没有被任何子任务所使用,则表示为0.如Pkm代表算法中第k次求解的第m维空间;Pkm=n-1表示算法中第k次求解中第m个资源粒子分配给第n-1个子任务使用.
在此粒子群优化算法中,采用了惩罚函数法[9]来处理了具有约束的优化问题,即只要是非可行解就直接丢弃.转化后的目标适应值计算公式可表示为式(8).

采用这种适应值计算方法,对式(4)经过多次优化迭代计算,即可求得其系统消费代价最小优化解.
协作求解的粒子群算法如下:
(1)随机初始化粒子种群:粒子群位置X、速度V、种群规模N、学习因子C1和C2、惯性因子w和最大迭代次数Max_Len以及系统参数变量pik,rik,cij值.
(2)利用给定的初始位置值,初始化个体最优位置Pi解和全局最优位置Pg解.并根据各个Agent自治性和社会交互性,利用式(2)(3)计算需求强度参数xik.
(3)While(k< =Max_Len&& φ <0.0001)//φ为优化达到的精度;
For i=1∶N
For j=1∶m
Change(X,V)//修改每个解的位置X和速度V.End For
(4)calculation(i);//通过式(8),计算第i次迭代适应值.
localbest(i);//将第i次计算解与所经历过的当前最好位置解Pi进行比较,若较好,则将其作为当前解的最好位置解;
End For
globalbest();//对每次求解,将其Pi与全局所经历的最好位置解进行比较,求出全局极值Pg.
EndWhile
4 仿真实例
4.1 仿真实例参数设置
在仿真实验中,考虑到每个子资源Agent和子任务Agent有不同的优先级、自治度、交互性等复杂的行为,在仿真实验中随机生成了相关系统参数.仿真程序中各个参数和变量分别设置如下:每次迭代中搜索空间的维数为资源数m;加速因子c1和c2设置为2.惯性权w根据经验值设为w=0.9 -count*0.5/(Max_Len -1),count代表当前第count个粒子.种群位置的变化范围根据所要研究的问题设置为[1,N],粒子速度的变化范围设定为[1,N];最大迭代次数Max_Len取值为500;其他参数设置为如下随机值:wij=[0,1];λ1= [0.01,0.1];λ2= [0.1,0.2];mi= [50,100];pik= [2,10];rik= [1,5];cij= [5,10];Sk= [100,200];Pk= [100,200].
4.2 仿真结果与收敛性分析
算法中的全局最优适应值变化反应了协作求解的寻优过程.种群根据自身经验和全局经验,不断调整单个解的位置,最后通过迭代搜索到全局最优解.由于本文把每个解的搜索空间定义为资源数.所以每个全局最优适应值就代表了任务资源的一次规划分配方案.在系统协作求解中,由于子任务数和子资源数是不固定的,并且协作求解的程度e也处于动态变化之中.因此,为了全面考察算法的有效性.本文针对不同的子任务、子资源和不同e值组合进行实验分析.如图3,4所示.
图3 给出了在 (m,n)=(12,10),e=0.3,0.5,0.8条件下全局最优适应值Pg的变化过程.从图3可以看出,当资源粒子数和任务粒子数相同,协作求解程度e不同时,全局最优适应值差别很大,由17.1变化到41.2,而收敛速度基本相同.这是因为随着e的增加,系统协作求解的资源消费不断增加,导致系统总消费不断增大.但由于资源数和任务数相同,每个粒子的搜索空间维数相同.因此算法的收敛速度基本相同.这也说明了该算法的收敛速度与协作求解程度e无关.当资源数和任务数不同,协作求解程度相同时.全局最优适应值虽变化很大,但收敛速度随资源粒子数的增加明显变慢.这是由于资源数的增加导致粒子搜索的空间变大,迭代速度就会变慢时间变长.如图4所示.在图4虽然全局最优适应值变化速度不同,但最终都趋于平稳状态.表明该方法具有良好的收敛性.同时,仿真结果也验证了该方法适合不同协作条件下各种任务资源规划分配求解.
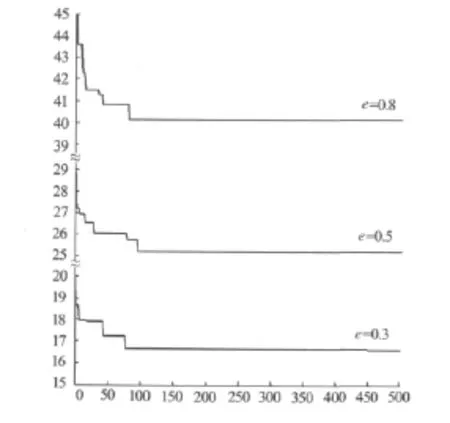
图3 全局最优适应值变化((m,n)=(12,10))
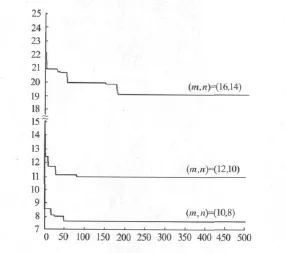
图4 全局最优适应值变化(e=0.2)
仿真计算过程中,对于不同的资源粒子数、任务粒子数和不同的e值.在run_time=30条件下,求得的全局最优适应平均值和标准方差值如附表所示.
在附表中全局最优适应值的标准均方差的变化范围为0.22~0.42.说明了该算法具有良好的收敛性和有效性.仿真结果也验证了该方法适合不同协作条件下各种任务资源规划分配求解,该方法具有一定的通用性和有效性.
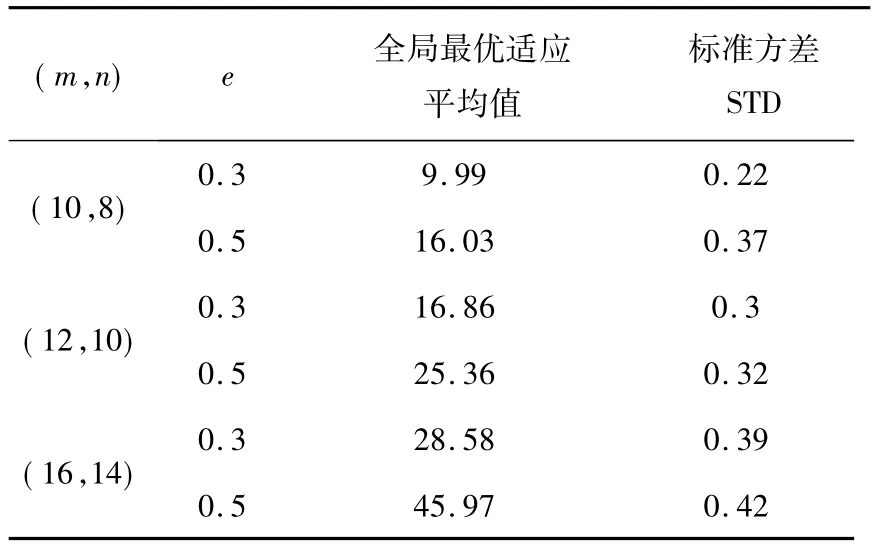
附表 任务资源规划分配结果表
5 结论
多Agent分布式系统协作求解比较复杂,需要考虑Agent本身的自治与交互行为动态性和随机性、复杂性等问题.本文针对分布式环境下任务资源协作规划分配问题,提出了一种多Agent分布式系统协作求解粒子模型方法,通过讨论多A-gent系统分布协作求解和粒子协作之间的关系,将协作求解问题转化为多个粒子共同寻优的过程,并构造了适合求解该方法的粒子群算法.在算法迭代过程中,尽管全局最优适应值收敛的速度不同,但都收敛达到平稳状态,表明该算法是收敛的.仿真实验结果表明在该方法中资源数的多少决定了算法的搜索空间,影响了收敛速度的快慢,但收敛速率与协作求解程度无关.仿真实验结果也验证了该模型方法即能克服了环境和Agent本身的动态变化,又能处理社会交互行为变化对系统协作求解的影响,能够很好地解决各种复杂的任务资源规划问题,具有很好的有效性和通用性.
[1]张新良,石纯一.多Agent合作求解[J].计算机科学,2003,30(8):100-103.
[2]李英.多Agent系统及其在预测与智能交通系统的应用[M].上海:华东理工大学出版社,2004.
[3]WOOLDRIDGE M,JENNINGS NR.The cooperative problem-solving process[J].Journal of Logic Computation,1999,9(4):563-592.
[4]SHUAI Dianxun,FENG Xiang.Distributed problem solving in multi-agent system:A spring net approach[J].IEEE Intelligent System,2005,20(4):66-74.
[5]帅典勋,王亮.一种新的基于复合弹簧网络的多A-gent系统分布式问题求解方法[J].计算机学报,2002,25(8):853-859.
[6]陶海军,王亚东,郭茂祖,等.基于熟人联盟及扩充合同网协议的多智能体协商模型[J].计算机研究与发展,2006,43(7):1155-1160.
[7]陈宇,陈新,陈新度,等.基于设备整体效能和多Agent的预测-反应式调度[J].计算机集成制造系统,2009,15(8):1599-1605.
[8]谢晓锋,张文俊,杨之廉.微粒群算法综述[J].控制与决策,2003,18(2):129-134.
[9]徐刚,于泳波.基于改进的微粒子算法求解0/1背包问题[J].齐齐哈尔大学学报,2007,23(1):71-74.
