脉冲扰动系统的集合稳定性

赵海清，张玉乐，王光雪

(大连交通大学 理学院，辽宁 大连 116028)＊

0 引言

人口动态，细胞分裂等一些数学模型都用脉冲系统来描述，因此近年来脉冲系统理论被广泛研究和发展.脉冲系统理论形成了很多不同的稳定性概念，如严格稳定性［1］，实际稳定性［2］以及两测度稳定性［3］等等.另外，由于实际到一个数学模型有时总有一些误差，而且由于机器老化等一些实际问题，使得一些模型总是有一些扰动存在.如果我们考虑这些扰动，便产生了一个扰动系统.对原来的无扰动系统，它通常需要满足某种稳定性，那么它所对应的扰动系统是否是稳定的呢?这需要我们进一步判断.可是不幸的是，我们除了知道扰动项的一些定性的信息，如扰动的范数的上界等条件，根本不知道扰动项的具体描述，因此我们就不能用已有的稳定性方法来判断.本文从扰动项上界这仅有的条件出发，研究了扰动脉冲微分系统的集合稳定性.之所以研究集合稳定性，是因为集合稳定性是包含零解的稳定性，解的稳定性的比较广泛的稳定性概念［4］.

具体地，我们是利用原始脉冲系统的稳定性和Lyapunov函数，考虑到扰动项的影响，研究了脉冲系统的集合的一致渐近稳定性，给出了集合稳定的充分性条件.本文的方法可以用来考虑一个复杂的脉冲系统的稳定性，只要把这个复杂的脉冲系统看成我们熟悉的或者能判断其稳定性的系统的扰动系统，根据我们定理的条件，便可以判断出这个复杂系统的稳定性.

1 研究系统及相关知识

Rn是一个定义了范数和距离的n维欧式空间.我们考虑下面这个扰动系统

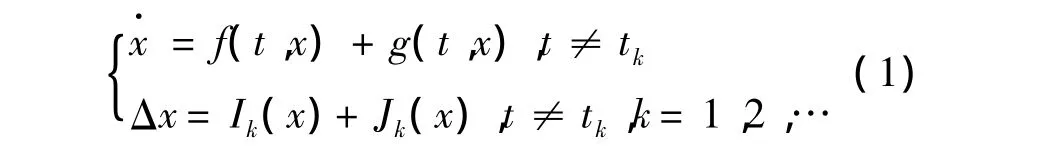
式中，t∈R+=［0，+∞)，x∈Rn，f:R+×Rn→Rn关于自变量t是逐段连续，在每个tk点左连续，Ik(x):Rn→Rn关于每个k连续，0＜t1＜t2＜… ＜tk＜…，当 k→ ∞，tk→ ∞，Δx(tk)=Ik(x(tk))+Jk(x(tk))，系统(1)是如下系统(2)的一个扰动系统

由于模型的偏差，机器老化等实际问题产生了扰动项g(t，x)，Jk(x)，有时我们不知道扰动项的具体表达或其一些定量性质，但是我们知道扰动项的范数的上界.本文将利用这个上界来解决扰动系统的一致渐近稳定问题.令x(t;t0，x0)是具有初值x()=x0的(1)的解.

定义下面的类

K={a|a:R+→R+是关于自变量严格递增的函数且a(0)=0};

Gk={(t，x)∈ R+× Rn，tk－1＜ t ＜ tk，且 tk预先给定};

M(t)={x∈ Rn:(t，x)∈ M};

M(t，ε)={x∈ Rn:d(x，M(t))＜ ε，ε ＞ 0};

Dη，t={x∈Rn:d(x，M(t))≤η，η＞ 0，t∈R+};

Sα={x∈ Rn:‖x‖ ＜ α，α ＞ 0}.

假设

(1)∀t∈R+，M(t)不是空集;且存在紧集Q⊂Rn，使得M(t)⊂ Q;

(2)对(t，x)，(t'，x)∈f+g，存在常数ρ使得|d(x，M(t))－ d(x，M(t＇))|≤ ρ|t－ t'|;

(3)对系统(1)的每个解满足:任意定义域内的 t，d(x(t;t0，x0)，M(t))≤ r ＜ ∞.

定义1 函数V:R+×Rn→R+属于ν0，下面的条件被满足

(2)在每个tk处 V是左连续的且右极限存在，特别是，当(t，x)∈ M 时，V(t，x)=0，否则，V(t，x)＞ 0.

定义3［5］如果下面的条件(1～3)成立，则关于系统(1)的集合M是一致全局渐近稳定的.

(i)M是稳定的:∀t0∈R+，∀ε＞0和∀α＞0，存在 δ(ε)＞ 0和∀x0∈Sa∩M(t0，δ)使得对t≥ t0，x(t)∈ M(t，ε);

(ii)系统(1)的解是有界的:∀t0∈R+，∀η＞0和 ∀α ＞ 0，存在β(ε)＞ 0和∀x0∈Sa∩Dη，t0使得对 t≥ t0，x(t)∈ M(t，β);

(iii)M是吸引的:∀t0∈R+，∀η ＞0，∀α ＞0和∀ε ＞ 0存在T(η，ε)＞ 0和∀x0∈Sa∩Dη，t0使得对 t≥ t0+T，x(t)∈ M(t，ε).

2 稳定性证明

引理 假设对t≥t0，m(t):R+→R在tk上左连续，对任意的k，D+m(t)≤l(t)m(t)+p(t)，m)≤ekm(tk)+qk，则，其中l(t)，p(t)是连续的，ek，qk是常数.

定理 设 a，b，c∈ K，λ(t)，θ(t)是可积正函数，且下面条件成立:

(i)a(d(x，M(t)))≤ V(t，x)≤ b(d(x，M(t)))，(t，x)∈ R+× Rn;

(ii)对系统(2)中的V(t，x)满足D+V(t，x)≤－ λ(t)V(t，x)，t≠ tk和 V(t+0，x+ Δx)≤ V(t，x)，t=tk;

(iii)||g(t，x)||≤ θ(t)a(d(x，M(t)))，且Lθ(t)＜ λ(t);

(iv)||Jk(x(tk))||≤ εka(d(x(tk)，M(tk)))，εk≥0和Lεk＜ ∞.

则M是系统(1)的一个一致全局渐近稳定集.

对 t≠ tk，

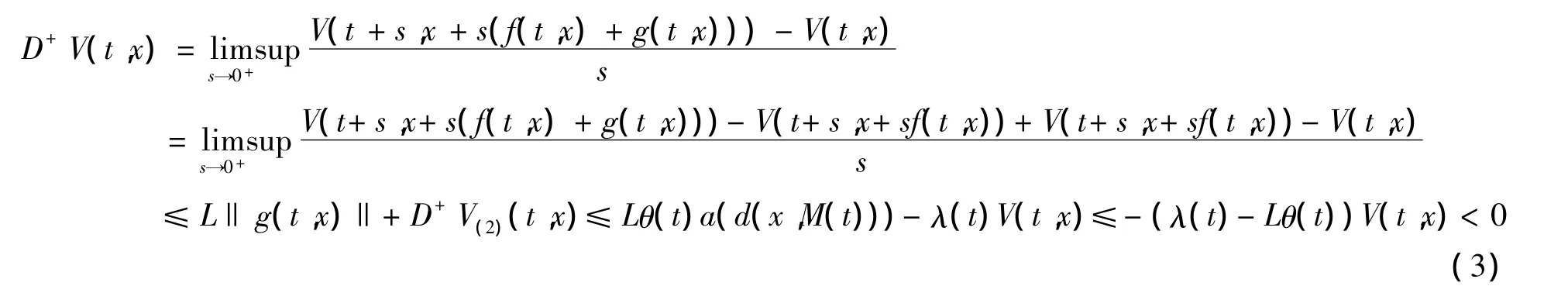
对t=tk，

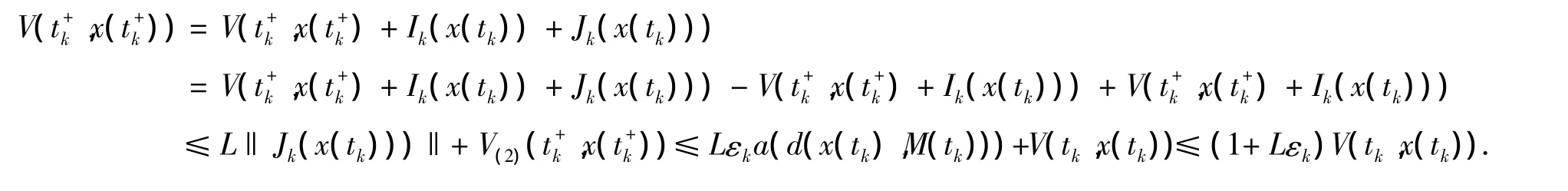
根据引理有

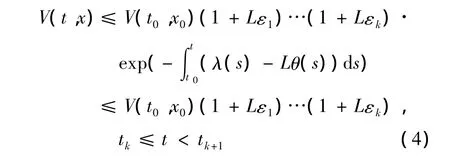
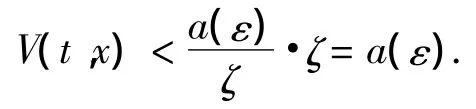
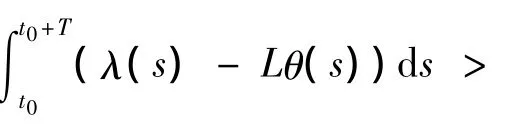
下面我们将证明对上面的T(η，ε)＞0，系统(1)的解满足对∀α ＞ 0，x0∈Sα∩Dη，t0，存在t*∈［t0，t0+T］，使得 d(x(t*)，M(t*))＜ δ.否则，对任意 T ＞ 0，t∈［t0，t0+T］有d(x(t)，M(t))≥δ.

根据(3)，有下面的式子

这是一个矛盾，所以存在t*∈［t0，t0+T］，使得d(x(t*)，M(t*))＜ δ.

根据式(4)，

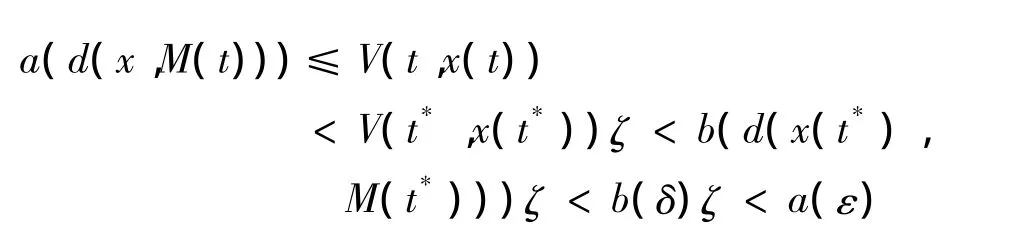
这就证明了M是一致全局吸引的.

对 ∀α ＞ 0，∀η ＞ 0，∀x0∈ Sα∩ Dη，t0，取β(α，η)使 a(β(α，η))＞ b(η)ζ.根据式(4)和(i)，有

这就证明了系统(1)的解是有界的，完成了定理的证明.

3 结论

本文利用Lyapunov函数，通过原始系统的稳定性解决了脉冲扰动系统的集合的全局一致渐近稳定性，该稳定性是包含零解一致渐近稳定的稳定性，具有广泛的意义，特别是，应用本文的稳定性条件能快速判断一个扰动系统的稳定性，因为它有了一个直接的Lyapunov函数.

［1］SENLIN LI，XINYU SONG，AN LI.Strict practical stability of nonlinear impulsive systems by employing two Lyapunov-like functions［J］.Nonlinear Analysis，2008(9):2262-2269.

［2］BORYSENKO S D，SPERANZA TOSCANO.Impulsive differential systems:The problem of stability and practical stability［J］.Nonlinear Analysis，2009，71:1843-1849.

［3］XINZHI LIN，QING WANG.On stability in terms of two measures for impulsive systems of functional differential equations［J］.J.Math.Anal.Appl.，2007，326:252-265.

［4］LASALLE J P.The extent of asymptotic stability［J］.Proc.Nat.Acad.Sci.，1960，46:363-365.

［5］KULEV G V，BAINOV D D.Global stability of sets for systems with impulses［J］.Applied Mathematics and Computation，1987，38:99-115.