基于GPU并行处理的图像快速旋转算法
2012-07-02李亚荣刘佳
李亚荣,刘佳
(大连交通大学 机械工程学院,辽宁 大连 116028)
0 引言
图形处理器(GPU),其概念相对于CPU,是一种专门用于处理图像的核心处理器.随着GPU性能的提升,并且GPU可编程操作,它广泛用于繁琐复杂的计算领域中,如图像和视频处理、计算生物学和化学、流体力学模拟、CT图像再现、光线跟踪等.特别是GPU在并行加速方面所具备的优势体现在[1]:①大量的并发式线程,②极高的运算密度,③显存的快速访问,④低数据耦合.因此加速计算方法正在从CPU“中央处理”向CPU与GPU“协同处理”的方向发展.为了实现协同处理的计算模式,NVIDIA公司发明了一致CUDA并行计算架构.该架构利用GPU的并行处理能力,可大幅度提升计算性能.
图形旋转是数字图像处理中常见的算法.传统的旋转算法中,CPU承担了所有的数值计算,当需要处理的图形达到几十或者上百兆时,CPU会耗费大量的计算时间,且为了保证图形的处理质量和精度,相对的会增加CPU的负荷,影响其它线程的运行.而普通的并行运算不仅硬件成本高,且原有的旋转算法无法适应并行运算的架构,因此,基于CUDA架构并行处理的图形旋转算法具有十分重要的意义,它将图形旋转繁琐的计算从CPU转移到GPU,利用GPU的强大性能极大地加快运行的速度.
1 现有的图像旋转算法及其特点
1.1 直接旋转法
笛卡尔坐标系中,将一个图像绕着坐标轴顺时针旋转α角度后,图1所示为旋转之前的图像,图2为旋转之后的图像,二者的坐标和旋转角度具有一定几何关系.

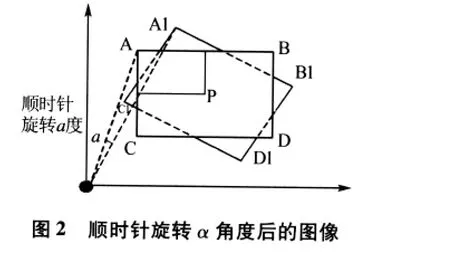
假设用(x0,y0)表示一幅xoy坐标系下的数字图像中的任意点,(x',y')为(x0,y0)旋转α角度后图像对应点.那么 (x,y)与(x',y')有如下的关系式:
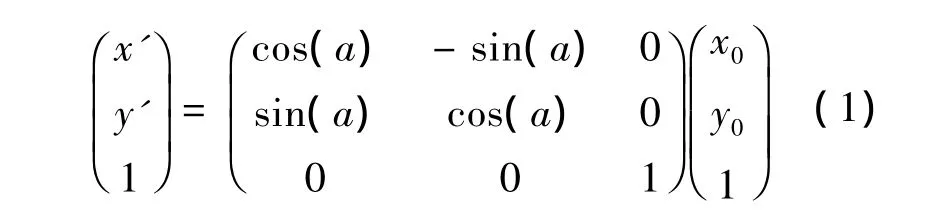
因为图像在旋转过程中引入三角函数sina,cosa值,这些值均为小于1的浮点数,而图像的坐标值只能为整数,因此很多点坐标需强制取整.这样很多像素取整后精度不够,即如果采用直接发由原始图像的各个像点对应到旋转后的图像像点,会造成图像的空洞.为了避免空洞,采取反向逆推法来求旋转后的点.即根据式(1)的逆运算公式求出原始图像.但是旋转图像和原始图像不是一一对应的映射关系,反向旋转方法求取的像素大多亦为浮点型[1],因此需要根据插值的方法来确定具体的像素值.
一般采用的插值法为最近邻插值算法[2]、线性插值算法[3]和高阶插值算法[4].由(1)式可知,直接法效率低,它对每个像素点进行后向映射和插值,并会产生大量的浮点取整运算,一次浮点数转化到整数的取整运算的时间开销很大,约为1次浮点数乘法开销的10倍[5],因此会增加CPU运算时间.
1.2 三步分解法
使用直接法计算图像旋转α角时,例如处理一幅大小为N×N的图像,由式(1)和式(2)可知需要4N2次浮点乘法以及2N2次浮点加法.由于浮点数的加法和乘法计算以及取整运算增加CPU运算时间,所以当N较大时,算法的运行速度非常缓慢.因此根据图像的错切[6]原理对于直接法进行优化得到新的算法——三步分解法.它提高了图像的旋转速度.三步分解法的基本原理如下:
根据矩阵变换的基本原理对于旋转矩阵R做如下变换:
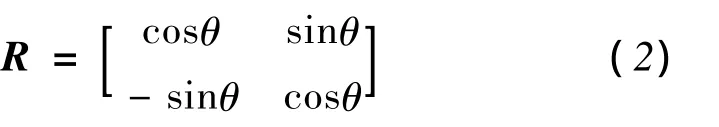
根据矩阵变换公式得到

根据上述变换,矩阵R被分解成三个矩阵相乘.由于数字图像处理在实现过程中多采用逆向映射法,因此对式(3)求逆矩阵得到了R逆矩阵R-1,可以得出三步法实现图像旋转的步骤如下图3所示.

图3 三步分解法实现的图像旋转
通过分析,在理论上三步法把直接法的o(n2)次取整运算简化到o(n)次,其效率优于直接法,减少了CPU的运行时间,但存在以下问题:①经过几次矩阵相乘(即平移计算),每次变换都进行插值,因此旋转后的图像精度会受到很大影响.②处理像素很高的图像时,三步法处理缓慢,在性能上仍具有缺陷.
2 基于GPU并行处理算法
分析以上两种传统旋转方法后,可见图像旋转算法性能的提升需要达到算法精度与时间复杂度两者的相互平衡.为了解决上述两种算法中的运算时间长、精度不高的问题,本文提出一种新的图像快速旋转算法来达到两者之间的平衡.该算法基于CUDA架构,且使用Bresenham画线算法在处理计算机绘制直线等基本图形元素时,可以避免大量的浮点及取整运算.
2.1 Bresenham划线算法原理
Bresenham算法采用递推步进的方法,即令每次变化方向的坐标步进一个像素,同时另一个方向的坐标依据误差判别式的符号来决定是否要步进一个像素[7].图4可见,下一个最近邻像素处于当前像素的八领域[8]中.设当前映射点为(x1,y1),由式(1)可知,下一个映射点

所有的映射点都在同一条直线上.设距离(x2,y2)最近的像素点为(m2,n2),根据最近邻像素八领域原理得出下一个与前一个像素点的关系为:素点保持不变且像素点向前偏移一个单位[9].
为了确定下一个像素点的位置,需引入Bresenham算法中误差项.记录映射点与最近邻接点之间的误差,定义x和y方向的误差为:mx=xm,my=y-n.更新为下一个邻结点时,首先需更新误差项:
(1)mx> 0.5,x ~ 0,mx=mx-1
(2)mx< 0.5,m 不变.
(3)my< -0.5,n=n+1,my=my-1
(4)my> -0.5,n不变.
此算法避免了大量的浮点乘法和取整运算,只需判别误差项即可定位最近领近像素点,减少了运算量.基于Bresnham画线算法的图像旋转算法如下:
(1)原有图像尺寸大小为(h0,w0),根据旋转的角度a值得到新的图像尺寸为(h1,w1).
(2)根据Bresenham算法原理开始计算每行每一个点的后向映射点的精确位置.
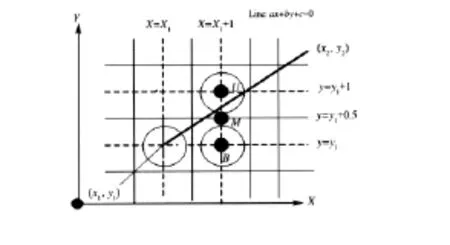
图4 Bresenham算法原理图
2.2 CUDA并行库优化
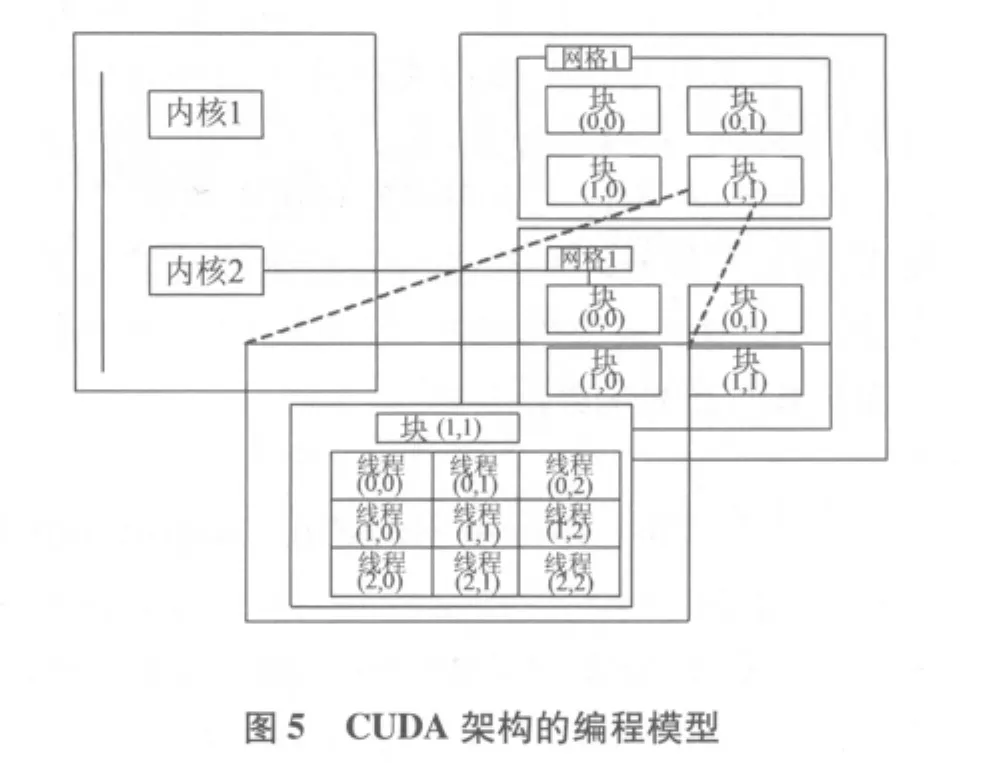
现使用CUDA并行库对Bresenham旋转算法中双层循环进行优化.GPU进行并行计算会加快算法旋转的速度.图5为CUDA架构的编程模型.
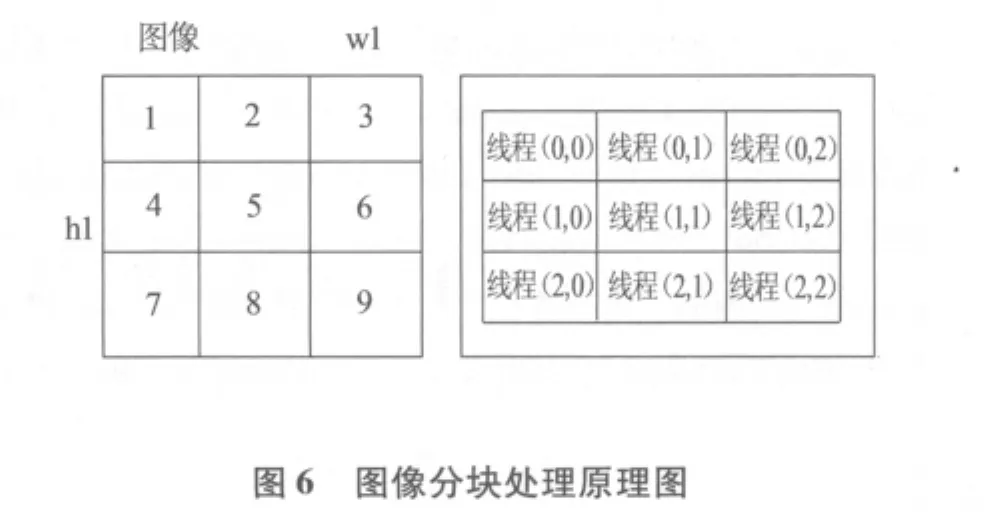
由图5可知,一个内核中存在着两个层次的并行,即网格中的块之间的并行以及块之间的线程并行.每个网格有若干个线程块组成,而每个线程块由若干个线程组成.内核以网格为单位执行并行,各网格之间是并行的.网格间无法通信,但是同一网格间的Thread可以通信.采用这种编程模式,既可以运行单个线程块的程序,又可以运行上百个线程块的程序.这样可以将基于Bresenham算法的图像旋转算法进行并行化.在CUDA中,一个线程块中的线程最多只能有512个,为了提高并行性,可以增加线程块的数量,这样会有更多的线程参与运算.设此时图片大小为w1×h1,令DATA_SIZE=w1×h1,所以每个线程处理的元素个数为DATA_SIZE/(blocks_num*threads_num).显卡的内存是DRAM,因此最有效率的存取方式是以连续方式进行存取.此时线程0读取第一个数字,线程1读取第二个数字,依此类推.所以,将原有的程序进行修改,每个线程处理图片的一部分,类似的原理如图6所示,此时将图片实现逻辑上的分块,每一块线程处理图片的一部分,根据GPU的体系结构,大量的线程可以并发执行,极大地提高了运行速度.当所有线程运行完毕后,从显存中拷贝数据回内存即可得到结果.
3 实验结果与结论
本实验平台为 Intel core Duo E6700,4GB RAM,GeForce GTX 560 Ti,操作系统是32位Windows XP.CUDA工具包版本为3.2.分别使用上述三种算法测试不同大小图像的旋转处理所花费的时间,其结果如附表所示(处理时间不包括主存与显存间的数据传输时间).时间单位:ms,图像数据大小以字节为单位.
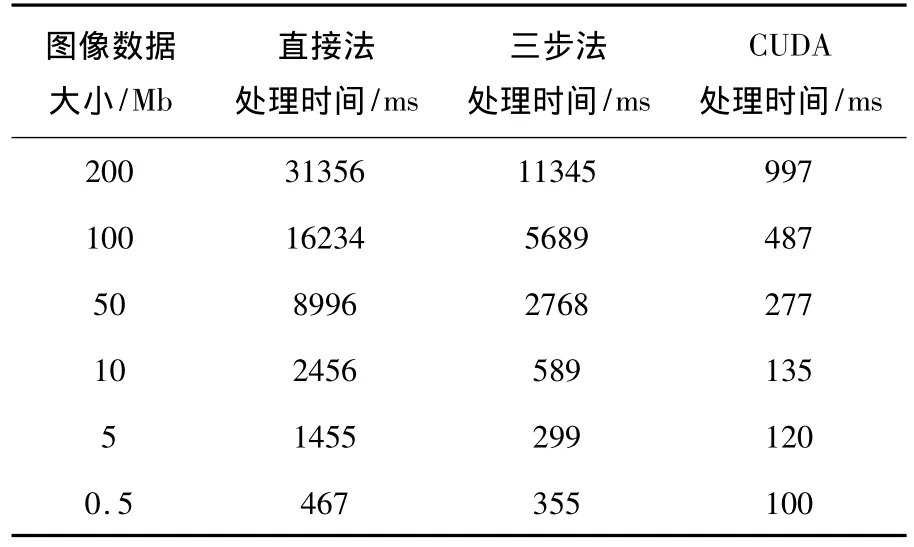
附表 三种算法在处理时间上的比较
由实验数据可知,图片越大,直接法和三步法耗时越长,无法满足图像实时处理方面的性能要求,而CUDA的加速性能却越明显;对于较小的图片,CUDA加速性能与其它两种算法性能相近.在GPU上使用CUDA架构实现算法的并行设计简单,关键需知道算法的哪些部分可使用GPU进行并行化处理.本论文中图像旋转属于像素级[10]操作,因此图像旋转算法进行并行化优化较易实现,性能也得到极大的提升.即使用GPU的并行处理具有明显的优势.
[1]胡海涛,平子良,吴斌.具有旋转不变性的图像矩的快速算法[J].光学学报,2010,30(2):394-398.
[2]刘鑫,姜超,冯存永,等.基于CUDA和OpenCV的图像并行处理方法研究[J].测绘科学,2011,20(1):178-181.
[3]梁娟娟,任开新,郭利财,等.CPU上的矩阵乘法的设计与实现[J].计算机系统应用,2011,20(1):178-181.
[4]刘耀林,邱飞岳,王丽萍.基于GPU的图像快速旋转算法的研究及实现[J].计算机工程与科学,2008,30(6):48-51.
[5]陈芳.图像旋转插值算法和基于链码技术计算图像几何矩的算法研究[D].上海:华东师范大学,2006.
[6]王滨海,许正飞,陈西广,等.图像旋转算法的分析与对比[J].光学与光电技术,2011,30(6):46-49.
[7]石慎,张艳宁,郗润平,等.基于Bresenham画线算法的图像快速-高精度旋转算法[J].计算机辅助设计与图形学学报,2008,19(11):1381-1397.
[8]RAFAEL C GONZALEZ,RACHARD E Woods.冈萨雷斯数字图像处理[M].北京:电子工业出版社,2009:51-55.
[9]孙勇国,文必龙,巴铀.机械工程图图像快速旋转算法[J].哈尔滨科学技术大学学报,1996,30(6):21-26.
[10]盖素丽.基于GPU的数字图像并行处理方法[J].电子产品世界,2009,30(6):39-40.
