接触非线性分析及对车下吊装联接结构螺栓可靠性的校验

兆文忠，蔡培培，王剑

(1.大连交通大学 交通运输学院，辽宁 大连 116028;2.大连交通大学 机械工程学院，辽宁 大连 116028)＊

0 引言

接触问题在工程中随处可见，例如典型的螺栓连接、铆钉连接、齿轮啮合以及摩擦和滑动，都是接触非线性问题.早在 19世纪 80年代，Hertz［1］就开始了接触问题的理论研究，但由于其力与变形之间的高度非线性关系，研究一度进展缓慢.近年来，随着计算数学和有限元技术的发展，接触问题的研究取得了显著进步.Christensen［2］研究了弹塑性摩擦接触问题，并将模型转化为非光滑方程组，之后用解B-可微方程组的牛顿法进行求解.Tin-Loi［3］在研究工作中考虑了无摩擦弹塑性接触问题，将其模型写成了混合互补模型，并用标准互补求解软件PATH进行了求解.钟万勰［4］等提出了分析弹塑性接触问题的参变量变分原理，在他们的方法中将接触问题和弹塑性问题都表示为参数二次规划问题，最终化为线性互补问题的求解.张洪武［5］采用正交各向异性摩擦定律对三维弹塑性摩擦接触问题进行分析，基于参变量变分原理给出了一个求解互补问题的非内点光滑化算法.

理论和算法的研究成果，促进了接触分析在工程实际中的应用.张洪武［6］采用有限元参数二次规划法，并结合多重子结构技术，求解了柴油机涡轮增压器叶轮与轴套、轴套与轴的三维弹塑性有摩擦接触问题，获得了叶轮、轴套与轴之间接触应力的相应分布规律.王小松［7］以弹性半空间非赫兹接触理论计算轮轨法向接触问题，得到比较真实的法向压力分布.赵卫平［8］采用通用有限元程序ANSYS对拔出试件进行了接触分析，实现了基于ANSYS接触分析的粘结-滑移的数值模拟.

接触分析能够更为真实的再现结构受力、变形过程.在当前铁路飞速发展的大环境下，安全可靠性的重要性日益凸显，对车辆关键部位进行接触分析成为必要工作.本文主要以接触非线性理论为基础，以新型城际动车车下吊装结构的联接螺栓为研究对象，采用接触分析手段校验螺栓联接的安全可靠性，为设计人员提供了计算模板.

1 接触问题的边界状态及其ANSYS实现

1.1 接触问题的边界状态［9］

接触问题是边界非线性，边界状态是随时变化的，如图1 所示构建局部坐标系η1、η2、η3，其单位基矢量为e1，e2，e3=n，其中n为物体A在接触点处的表面的单位外法线矢量.可由如下公式判断接触状态:

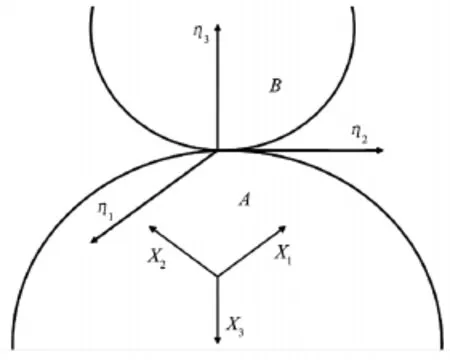
图1 接触问题的边界状态示意图

在分离状态有位移条件和面力条件:

粘结接触状态有位移条件和面力条件:

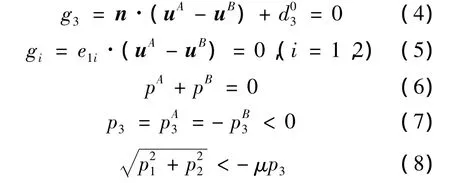
对滑动接触状态有位移条件和面力条件:

以上各式中，u为位移矢量;pi、gi分别为三个局部坐标方向的接触面力和间隙量;上标A、B分别表示物体A和B;d03为接触点对初始间距;μ为摩擦系数.

1.2 接触问题的ANSYS实现

非线性有限元分析过程中，程序需要通过不断判断边界状态，进而进行接触有限元计算.大型通用软件ANSYS具有强大的接触判断与分析计算能力，可以很好的模拟接触非线性问题的边界变化状态.ANSYS主要有三种接触方式:点─点接触，点─面接触，面─面接触［10］.对面面接触单元来说，一般分为刚体─柔体、柔体─柔体两种类型.具体操作中，刚性面一般都被当作目标面，可以使用Targe169和Targe170来实现目标面的模拟，柔性体的表面一般被当作接触面使用，可以使用 Conta171，Conta172，Conta173，Conta174 等单元来实现接触面的模拟.一个目标单元和一个接触单元构成一个接触对.程序通过一个共享的实常数识别和使用接触对.

ANSYS的面─面接触单元对接触问题具有较好的的适应性，本文模型计算主要就采用面－面接触单元进行模拟计算.

2 有限元模型

2.1 有限元模型的建立

基于上述接触非线性理论及其ANSYS实现过程，本文对某工厂设计的新型城际动车车下吊装结构(变压器单元)进行了接触非线性有限元分析，主要校核了吊装连接结构的螺栓强度.

车下吊装组成如图2所示.变压器安装重量为4 t，由于设备重量大，运行过程中螺栓工作状体显得尤为重要，因此有必要对螺栓进行精细建模，进行接触非线性分析.

吊装通过16个M24螺栓与车体连接.使用Pro/E软件建立车下变压器整体三维模型，然后三维模型文件导入到Hypermesh软件中进行网格划分.

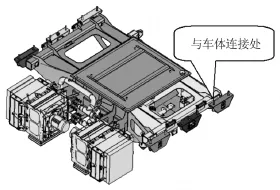
图2 M24连接处

在Hypermesh中适当简化三维模型，车体底部和设备框架采用壳元建模，吊装结构与车体连接位置的吊座采用实体建模，整体结构有限元模型如图3所示.其中，纵向限位器使用直径8 mm的螺栓，中间吊座使用直径20 mm螺栓，两边吊座使用直径24 mm螺栓，如图4所示，螺栓材料属性:密度ρ=7 850 kg/m3;弹性模量E=2.1e+5 MPa;泊松比ν=0.3;屈服强度为450 MPa.螺栓施加预紧力矩为470 N·m.

图3 变压器有限元模型

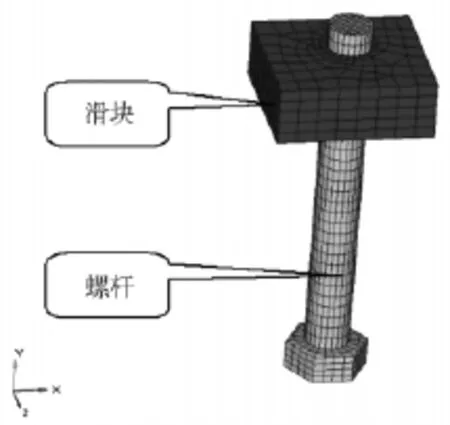
图4 M24螺栓

对螺栓连接建立接触对，螺栓在车下吊装结构中连接关系及接触状态如图5～7所示:

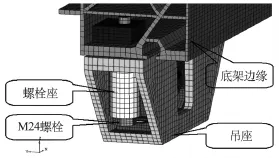
图5 M24螺栓连接

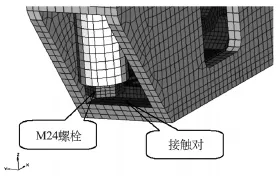
图7 吊座与弹性体的接触

2.2 计算工况

参考EN 12663标准，并考虑行车过程中最恶劣的情况，计算工况按下列8种组合工况考虑如表1所示，这里，c为垂向动荷系数，在车辆端部时取2，呈线性下降到车辆中部时为0.5，这里，c近似取为 0.5.

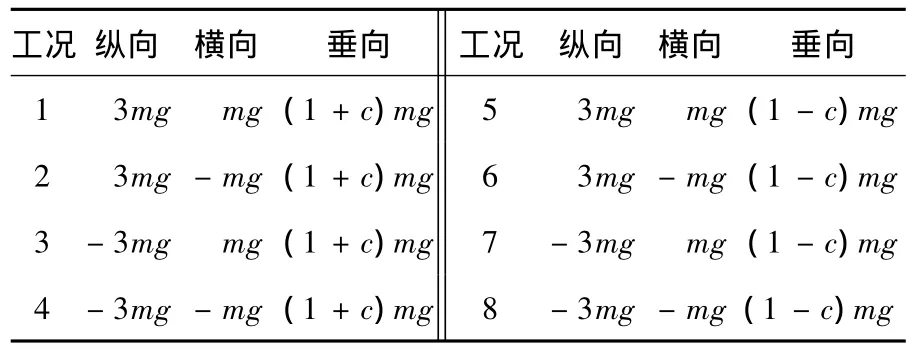
表1 组合工况

3 数值分析

按上述计算工况进行计算，所有接触类型设置为Standard，采用更新的Lagrange方法，法向刚度和侵入比分别设置为0.8和0.2.载荷分为30个载荷步，采用力收敛准则.经过迭代计算，得到非线性计算结果.

吊装结构中M8螺栓、M20螺栓、M24螺栓螺杆最大应力见表2，应力最大工况下下螺栓应力云图如图8～10所示.

表2 吊装结构螺栓应力统计表 kPa

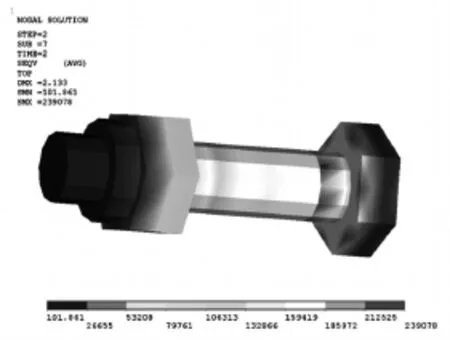
图8 M8螺栓螺杆应力云图

图9 M20螺栓螺杆应力云图

图10 M24螺栓螺杆最大应力云图

由计算结果得知，螺栓应力主要来自于预紧力工况，工作工况对螺栓应力影响不大，螺栓应力主要集中在螺杆根部.因此科学的制定预紧力方案十分重要.

4 结论

本文基于接触非线性理论，对新型城际动车车下变压器吊装结构进行了接触非线性有限元分析，校核了吊装连接结构的螺栓强度.结果显示，螺栓预紧力对螺栓应力影响较大，最大螺栓应力一般出现在螺杆根部，应力结果显示，吊装结构的螺栓连接结构满足结构强度要求.

通过本文工作还得到如下经验:在接触非线性有限元的ANSYS实现过程中，基本接触理论的理解对正确建模与否起着至关重要的作用，这是非常重要的一点;在接触建模过程中，精细建模是基础，网格质量、预紧截面的生成对计算精度和收敛速度有显著影响.

利用本文方法，可以对复杂结构进行精细分析，得到连接螺栓应力分布情况，为工程设计提供理论依据和指导.

［1］HERTZ H.On the contact of elastic solids［J］.J.reine angew.Math，1881，92:156-171.

［2］CHRISTENSEN PW.A semi-smooth Newton method for elasto-plastic contact problems［J］.International journal of solids and structures，2002，39(8):2323-2341.

［3］TIN-LOI F，XIA S.Nonholonomic elastoplastic analysis involving unilateral frictionless contact as a mixed complementarity problem［J］.Computer methods in applied mechanics and engineering，2001，190(35-36):4551-4568.

［4］钟万勰，张洪武，吴承伟.参变量变分原理及其在工程中的应用［M］.北京:科学出版社，1997.

［5］张洪武，何素艳，李兴斯.正交各向异性弹塑性摩擦接触问题的数值求解［J］.固体力学学报，2004，25(4):411-416.

［6］张洪武，廖爱华，吴昌华.压气机过盈配合的弹塑性有摩擦接触的研究［J］.工程力学，2007，24(1):186-192.

［7］王小松，葛耀君，吴定俊.非赫兹接触下轮轨接触蠕滑力的计算［J］.铁道学报，2007，29(4):96-100.

［8］赵卫平.基于ANSYS接触分析的粘结－滑移数值模拟［J］.建筑科学与工程学报，2011，28(2):44-51.

［9］郭乙木，陶伟明，庄茁.线性与非线性有限元及其应用［M］.北京:机械工业出版社，2005:247-260.

［10］马鸿峰.基于ANSYS的冷却运输机输送链接触有限元分析［J］.新技术新工艺，2011(1):21-23.