考虑使用环境的周转备件需求预测

孟祥辉，郑 毅，戴 荣

(1.91872 部队，北京 102442;2.装甲兵工程学院，北京 100072)

装备使用环境(operational environment)是指装备实际使用过程中所处的环境状态，包括使用部位环境、对损坏的敏感性、气候与地理条件、操作人员技能影响等，其对装备的可靠性都有重要影响。现有文献多将备件寿命作为主要的输入，并认为备件需求量为基准故障率(baseline failure rate)与工作时间的函数，很少考虑其他因素的影响［1-2］。显然，仅依据基准故障率与工作时间确定的备件理论需求量必然与备件实际消耗量存在较大的偏差。为更合理地获得备件需求，需研究其他影响因素对备件需求率的影响。其中，除动用方式和维修保障模式外，使用环境因素影响最为显著。

如何将这些影响因素进行定量化，构建故障率、使用环境与备件需求之间的关系是一个有待研究的问题。为此，本文将使用环境影响因素称为风险因素或协变量(covariant)，试着将使用环境纳入备件需求确定中，建立基于使用环境的备件需求比例危害模型，以确定更合理的备件需求量。

1 比例危害模型概述

令T 表示某系统工作时间，则发生故障前其可靠工作的概率函数可定义为

其中:F(t)和f(t)分别表示发生故障前正常工作时间小于T的分布函数和概率密度函数。则系统的故障函数可定义为

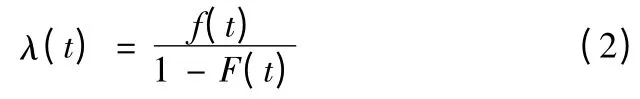
上述函数就是典型的故障密度函数。如前所述，一般情况下系统的故障率不仅受到时间影响，也受到工作时使用环境因素产生的协变量影响。因此，系统的故障率取决于仅与工作时间有关的基准故障率λ0(t)和其他与时间无关的、大量协变量并发影响的正函数。假设协变量不影响故障模式变化，即基准故障是不变，等于全体故障模式的故障率之和。但实际情况是由使用环境产生的协变量可能影响故障率，因而，观察到的使用过程中的实际故障率相对于基准故障率来说，或高或低。图1 描述了协变量对系统故障率的影响。

图1 使用环境协变量对系统故障率的影响

PH 模型是由Cox 最早在1972年提出的，主要运用于医学数据和工程可靠性问题的分析，近年来在装备状态检测领域也得到了较好的应用，一般称之为Cox 回归模型或PH 模型［3-5］。由PH 模型可知，协变量对故障函数具有乘法效应，即

式中:λ0(t)为基准故障函数，即ψ(Z，α)=1 时下的标准风险函数，对应不同的寿命数据，λ0(t)可为具体设定的指数分布、威布尔分布、正态分布等;Z 为与系统相关的使用环境协变量向量;α 为协变量向量Z 对系统的影响，即各协变量的回归系数。

2 基于使用环境的周转备件需求预测建模

2.1 基于寿命分布的周转备件基准需求预测模型

在装备研制、试验及部队试用过程中，工业部门应通过保障性分析确定各零部件的故障率，并在试验和试用中对其修正。将此阶段获得的备件故障函数定义为基准风险函数是合适的。而备件寿命分布规律不同，其需求预测模型也不一样。目前，常用的备件寿命分布模型有指数分布、威布尔分布、正态分布等，对应的备件需求预测模型为泊松分布、威布尔分布和正态分布模型［6-7］。下面根据产品寿命分布规律，建立周转备件基准需求预测模型。

假设备件满足率为P，备件预计需求量为S，则各分布模型对应的备件需求预测模型。

1)泊松分布预测模型

当备件寿命服从指数分布时，对应的备件需求服从泊松分布。对应的周转备件需求量为

式中:K 为单装同一备件数量，也称单车基数;t 为装备周转备件订货周期内累计有效工作时间;S 为订货周期内备件预计需求量。

当Kλt ＞5 时，备件需求量可以用正态分布近似计算，公式简化为

式中UP为正态分布分位数，可从GB/T4086.1 中查出。

2)正态分布预测模型

当备件寿命服从正态分布规律时，令备件的寿命期望值为E，标准差为σ，备件订货周期内累计有效工作时间为t(如果是磨损寿命，t 为累计工作时间;如果是老化、腐蚀寿命件，t 可用日历时间近似)，则备件预计需求量为

式中其他符号同式(5)。

3)威布尔分布预测模型

由于威布尔分布可以通过改变形状参数、尺度参数和位置参数来描述递增、递减的情况，得到不同的失效率曲线，可较好的拟合浴盘曲线，在可靠性工程中被广泛应用。备件寿命服从威布尔分布，设其形状参数为β，尺度参数为η，则备件预计需求量为

当为指数分布时，ν=1。其他符号同式(5)。

2.2 基于PH 的周转备件需求预测模型构建

备件在不同的使用环境中，其故障机理是相同的，只是与相关影响因素成一定的比例关系;同样，由可靠性理论可知，不同类型的备件在同一环境中，其故障的直接影响因素是不同的。如机械产品，锈蚀、磨损、压力等对其可靠性影响较大;而电子产品，受环境温度、相对湿度、电磁场等影响较大。不同类型的备件，需要进行不同的考虑和分析。求使用环境对周转备件需求量影响的关键是确定主要的风险影响因素zi及对系统的影响αi，根据前面备件需求预测模型确定使用环境影响下的周转备件需求量预测模型。

2.2.1 使用环境风险因素协变量及其权重确定

根据统计推理中协变量及其重要度的方法，可得具体分析与运算步骤:

1)统计不同地域同类装备的平均故障间隔时间数据ti(i=1，2，…，m)，并分析对应的使用环境风险因素协变量zj的影响等级αij(j=1，2，…，n)。为处理方便，一般将协变量影响等级分为2 个等级，依次为1，-1，分别表示影响不大和影响大。如风沙影响，1 表示风沙较小，如南方、西南和华北地区，-1 表示风沙大，如西北地区。

表1 统计TBF、Z 与影响等级对应表

2)采用Delphi 法或模糊综合评判法，估计各协变量对系统可靠性的影响权重lj，并对其进行一致性检验。

3)获得各协变量对系统的影响权重，并排除权重影响较小的风险因素，保留权重和不小于某一规定值(一般取0.9)的k 个协变量，作为影响系统的主要协变量因素。

4)得到考虑使用环境影响下的故障函数表达式，即

目前，相关的统计分析软件可以完成以上工作，如SPSS17.0、SYSTAT12 等。

2.2.2 使用环境影响下的周转备件需求预测建模

对各分布预测模型进行分析，可得到对应的PH 预测模型。

1)考虑使用环境影响的泊松分布预测模型

由式(8)可知，各协变量纳入泊松分布故障函数中可得到使用环境影响下的周转备件需求预测模型为

对应的经验计算公式为

式(10)也可适用于正态分布。同理，可以得到使用环境影响下的周转备件需求威布尔分布PH 模型。

2)考虑使用环境影响的威布尔分布预测模型

设不考虑使用环境时的形状参数为β0，尺度参数为η0;将各协变量纳入威布尔分布故障函数中得到的协变量模型为

对应的形状参数和尺度参数变为

式(12)表明，形状参数在不同的使用环境下不发生改变，尺度参数在不同的使用环境下是不同的，即不同的使用环境只能加速或延缓备件故障的发生，而不能改变故障模式。将式(12)所得形状参数和尺度参数代入式(7)，即可得到考虑使用环境的备件预计量。

从上面所得到的公式可知，当备件基准故障率λ0(t)或基准更换周期确定时，统计不同地域部队使用环境的影响，就可得到不同地域基于使用环境的周转备件需求量确定标准。

3 案例分析

以某部队的某型步兵战车负重轮为例，对其2007—2010年消耗情况进行统计分析。该单位地处东南沿海地区，经过分析可知，在使用过程中使用环境对负重轮的影响因素有:路面颠簸及阻力状况、温度、灰尘、盐雾值、操作人员技能等。各影响因素做如下假设:

1)路面状况。用于说明路面颠簸及阻力对负重轮油封造成的变形影响。1 表示一般路面影响，如水泥、柏油路;-1表示其他路面影响，如山地、岸滩、水稻田等。

2)温度。用于说明备件使用部位温度的影响。1 表示使用部位温度无明显影响，取0 ～35 ℃之间;其他温度为-1。

3)盐雾。表示盐雾值对故障的影响。1 表示盐雾侵蚀不明显，如内陆训练;-1 表示盐雾侵蚀明显，海滩和海上训练可取-1。

4)灰尘。表示灰尘的影响。1 表示灰尘无关紧要，如细泥土;-1 表示影响较大，如戈壁沙石、沙滩。

5)操作人员技能。该因素对油封的故障率有明显影响。1 表示熟练驾驶员操作，-1 表示生手操作。

有关温度、盐雾值的数据，可从历年的《中国统计年鉴》中获得。

在装备动用过程中，多个负重轮同时工作(如1 台装备10 个负重轮);再者，动用过程中，多台装备同时动用，将负重轮的消耗看作服从泊松分布是合适的;从泊松分布规律来看，其备件消耗量基本保持恒定，且主要采用事后维修和定期检修的方式，因此，将所属全部装备历次负重轮更换间隔工作总时间折算后作为负重轮消耗数据是合理的。对应的，考虑使用环境协变量影响下的负重轮消耗统计数据如表2所示。

表2 使用环境协变量影响下的负重轮消耗统计数据

利用SPSS Statistics 17.0 对以上数据进行相应处理，可得到各协变量对负重轮的影响权重。处理结果见表3 与表4。

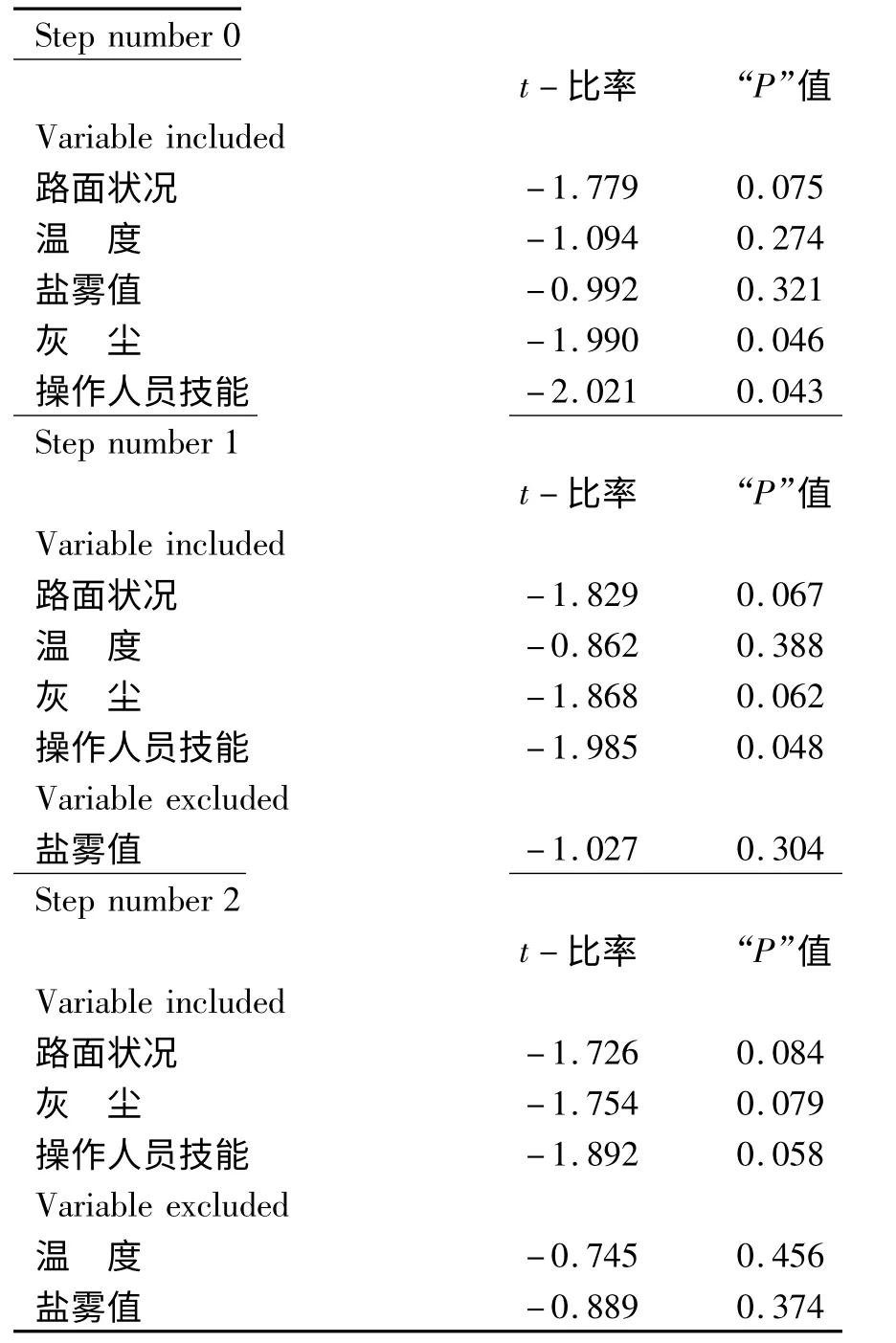
表3 协变量预计分析过程及结果

表4 分析结果模型归纳

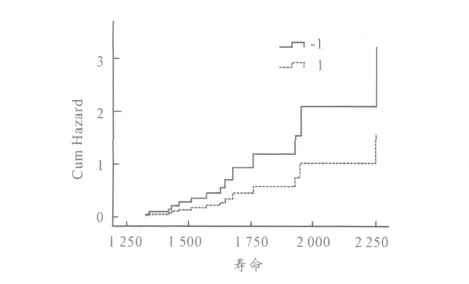
图2 以操作人员技能为例的更换率协变量分析

显然，用更换间隔时间代替平均故障间隔时间更加符合实际。将协变量权重值代入式(8)，即可得到考虑使用环境影响的备件更换率计算公式。假设负重轮的平均不定期更换间隔时间为3 000 h，当有多台装备时可认为其服从泊松分布，则基本更换率是一个常数

假设本例中驾驶员为新驾驶员，灰尘影响较小，路况一般。所以根据此情况可得:

对应的平均不定期更换间隔时间为1 960 h。该步兵战车单台装有负重轮k=10 个;假设该单位有100 台04 式步兵战车，单装年动用时间为50 h，全年摩托小时消耗为t=100 ×50 =5 000 h。在任一供应周期内，周转备件可用度应为90%，预计一个供应周期内(假定供应周期为1年)所需负重轮数量，令:

在理想状态下，没有协变量的存在，所需负重轮数量为

当i=22 时，P=0.918 5 ＞0.90，即S=22 个/年。

4 结束语

由以上分析和计算可知，考虑或不考虑装备使用环境影响，对周转备件的影响较大。在确定早期的周转备件需求量时，应根据不同地域和单位的使用环境确定周转备件需求量，以确定合理的周转备件消耗标准。

［1］叶心太，余仁波.装备保障中备件需求量确定方法研究［J］.舰船电子工程，2010(5):155-156.

［2］杨秉喜.GJB4355《备件供应规划要求》实施指南［M］.北京:总装备部技术基础管理中心，2006.

［3］戎翔，左洪福，张海军.视情维修策略下的民航发动机拆换时间预测研究［J］.机械科学与技术，2008，27(5):583-587.

［4］Ghodrati B.，Kumar U.Operating environment based spare parts forecasting and logistics — a case study［J］.International Journal of Logistics:Research and Applications，2005，8(2):95-105.

［5］Behzad Ghodrati. Reliability and operating environment based spare parts planning［D］.Sweden:the Doctoral thesis of Lulea University of Technology，2005.

［6］王磊，刘文宝，孟祥辉.基于耗损规律的装备维修备件确定方法探讨［C］//装备保障支撑理论与关键技术研讨会论文集.北京:兵器工业出版社，2006:465-468.

［7］孙伟，高连华，曹玉坤，等.装甲车辆可靠性理论与应用［M］.北京:兵器工业出版社，2006.

［8］中华人民共和国国家统计局.中国统计年鉴2009［M］.北京:中国统计出版社，2009.