复杂网络理论在对等网络特性分析中的应用✴

彭浩，陆松年，，赵丹丹，李生红，，张爱新

（1.上海交通大学电子工程系，上海200240；2.上海交通大学信息安全学院，上海200240）

复杂网络理论在对等网络特性分析中的应用✴

彭浩1，陆松年1，2，赵丹丹1，李生红1，2，张爱新2

（1.上海交通大学电子工程系，上海200240；2.上海交通大学信息安全学院，上海200240）

基于现有的复杂网络理论，研究了对等网络的复杂特性，并就对等网络中节点度和节点间平均最短路径两个特征参数进行算法设计和仿真。仿真结果表明，对等网络中使用复杂网络理论的特性分析理论结果与实验结果基本一致，能准确反映对等网络的特性。

对等网络；复杂网络；节点的度；最短路径长度

1 引言

近年来对等网络的应用越来越广泛，如文件和数据共享及存储、远程协同、并行计算等［1-2］，在这些领域中对等网络发挥着越来越重要的作用。但是，在上述对等网络的应用研究中，研究的重点都集中在保证系统性能和安全传输上［3］，没有对网络中的节点行为进行合理分析与研究，而节点的行为特征与整个网络系统的性能密不可分。复杂网络理论［4-5］作为分析复杂网络系统性能的有效工具，已经渗透到许多实际网络系统的研究与设计中。具体来说，对于现实网络系统的节点行为方式，使用复杂网络理论中的平均路径长度、聚类系数、节点的度分布等要素，能很好地描述节点行为特征。因而，复杂网络理论逐渐成为研究复杂网络系统的重要工具。

本文利用复杂网络理论，对对等网络系统节点行为的特征进行了分析，通过这些特征参数，我们能深入了解对等网络系统节点的行为，从而帮助我们优化对等网络系统的设计，更好地发挥对等网络的性能。

2 复杂网络相关理论

2.1 节点的度

节点的度是复杂网络理论中描述具体节点的很重要的一个特征参数。一般的定义，节点的度是指整个网络系统中与该节点连接的其他节点的数目。特别地，对于有向网络系统来说，节点的度还分节点的入度与节点的出度两种类型。根据节点的度的大小能定量地反映该节点在网络系统中的重要程度，度越大意味着该节点在网络中的地位越重要。

2.2 节点间的平均路径长度

复杂网络理论里，节点间的平均路径长度是指系统中任意两个节点之间距离的平均值。尽管实际网络系统的规模庞大，节点数目惊人，但是网络的平均路径长度却小得惊人。从这个角度上看，复杂网络系统是具有小世界效应的。

2.3 复杂网络模型

要很好地理解网络结构与网络节点行为之间的关系，就必须对网络的模型进行分类研究。在复杂网络理论里，描述复杂网络系统的模型主要包括规则网络模型、随机网络模型、小世界网络模型与无标度网络模型4种。

（1）规则网络模型

最初的网络模型多采用规则网络结构，如完全规则的全局耦合网络及最近邻耦合网络，前者过于稠密而后者又显稀疏，因而不能准确反映实际网络结构和节点行为特征。

（2）随机网络模型

随机网络起源于两位匈牙利数学家在1960提出的ER随机图模型［6］，该网络模型描述了从多个网络节点通过相同的概率p随机相连而形成网络系统的过程。后来在ER随机图的基础上，许多学者提出了不同概率的随机连接思想实现扩展的ER模型［7］。

（3）小世界网络模型

现实生活的实际网络既不是完全随机的也不是完全规则的。康奈尔大学的Watts［8］等人揭示了一种小世界网络模型的雏形，并且在《Nature》杂志上发表了一篇题为《小世界网络的群体动力学行为》的论文，这篇论文揭示了复杂网络的小世界特性。

（4）无标度网络模型

上面的随机网络模型与小世界网络模型都属于均匀网络，网络的分布模型可以用泊松分布来表示。所谓无标度网络模型，是指网络的度分布在网络节点度的平均值附近出现峰值，然后迅速出现衰减的一种网络度分布模型。

3 对等网络的特征分析

对等网络系统中，各个节点地位平等，不对任何系统中的节点强加任何属性，任意节点可以自由地加入或离开该对等网络，这样就给整个网络的拓扑结构带来了随机性。传统上对这种类型的网络进行理论建模分析时，一般采用的是随机网络模型，但是随机网络模型并不能准确地描述这些网络的某些特性，例如节点度的概率分布、平均最短路径长度、网络节点的聚集度以及在受攻击情况下的网络分布特性等。基于上述这些理论分析与现实需求，本文利用复杂网络理论，分析对等网络的节点度分布以及最小路径长度等重点特征参数。

（1）对等网络节点的度分析

前面提到了复杂网络系统中节点度的相关概念，这里我们结合对等网络对等、动态、随机的特点，可以看出，最直观描述该网络的模型就是随机网络模型和无标度网络模型。因此，本节对对等网络节点度的描述，是以随机网络模型与无标度网络模型中的度的设置进行改进得出的。

在随机网络模型中，节点之间是以一定的概率随机连接在一起。这里我们假定对等网络中有N

个节点，网络内部各节点之间都以一定的概率p随机连接，并独立于其他节点之间的联系独立存在。对等网络中节点的度，这里我们是指与某个节点相连接的节点的数目。令对等网络中N个节点的平均度为¯n，由于各个节点之间的联系是独立的，那么随机概率p可以表示为p=¯n／N-1，这样在对等网络系统中，节点度为n的概率可以表示如下：

由等式（1）可以看出，在N值取极值时，对等网络中节点的度呈泊松分布。在实际的复杂网络系统中，许多网络节点的度分布有时候呈幂律分布。设置方法如下：

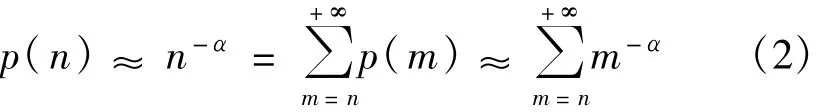
公式（2）是利用累积分布函数经过改进设计得出，这样可以消除原始幂律分布函数的消极影响，同时还保持网络的幂律特性。因此，本文对对等网络系统中节点度的分析，主要是利用公式（2）的计算得出。在本文第四节的仿真中，我们对公式（1）和（2）反映节点度的结果分别进行比较，得出最适合对等网络系统的节点度的计算方法。

（2）对等网络的节点间平均最短路径分析

在本文的第二节提到节点间平均路径长度的概念，这里我们也要借鉴其中的概念。另外，这里分析对等网络中的最小路径长度，需要介绍Newman［3］等人提出的节点度分布的生成函数。

定义1：设对等网络系统中包含N个节点，则该网络中任意节点度分布的生成函数可以表示成：

式中，pn表示对等网络系统中节点度为n的概率，并且满足F（1）=1。这里生成函数具有以下性质：

性质1：在概率pn所定义的概率空间里，所有N个节点的平均度可以用定义1中的生成函数表示如下：

性质2：对等网络中任意节点互相独立、地位平等，那么m个节点的联合生成函数可以用单个节点生成函数的m次幂获得。下面，我们以两个节点为例来具体说明该性质：

由上面公式可以看出，xn的系数是对等网络系统中两个节点的度之和为n的pipj之和，不难验证，高阶次的n同样满足性质2，这里不进行验证。

下面根据上述两个性质来计算对等网络系统中任意节点间的路径长度。假定对等网络中存在一度为n的节点，则对等网络中任意节点连接到该节点的概率与该节点的度成正比。这样，任意节点能连接到该节点的概率的生成函数可以表示如下：

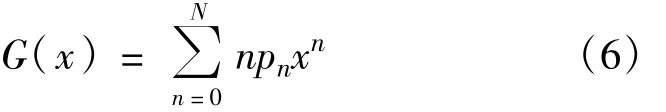
对上述公式进行归一化处理，可以得到

对于上面随机选择的度为n的节点，从该节点出发，可以直接达到与该节点连接的节点，然后可以向下到达下面一层连接的节点，以此类推。这样，沿着上述任意一条路径访问某个节点时，与该节点连接的其他节点数的分布的生成函数可以表示如下：

由性质2可知，对于对等网络中某一特定的节点，它的第二层相连的节点（也就是与第一层节点直接相连的其他节点）总数的概率分布生成函数可以表示为

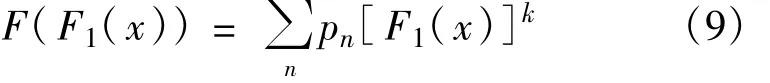
与上述公式类似，可以推算与网络中某一特定的节点相连的第三层相连的节点总数的概率分布生成函数可以表示为F（F1（F1（x））），以此类推其他各层相连节点的。这样根据公式（9）可知，与该节点第二层相连的所有节点平均度可以计算如下：

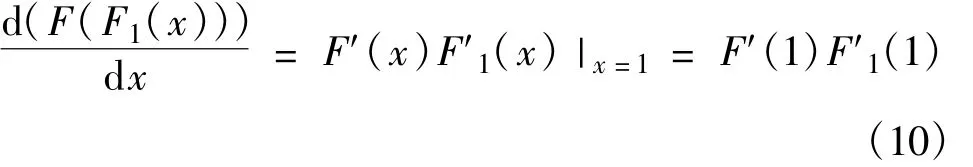
由公式（4）与公式（10）可知与对等网络系统中指定节点相连的节点以及第二层接连的节点的度的平均度。将公式（2）分别代入式（4）和式（10），假定对等网络系统中节点度的最大值为nmax，则有

由文献［9］可知，对具有N个节点的幂律指数为α的复杂网络系统而言，所有节点的最大度可以表示如下：

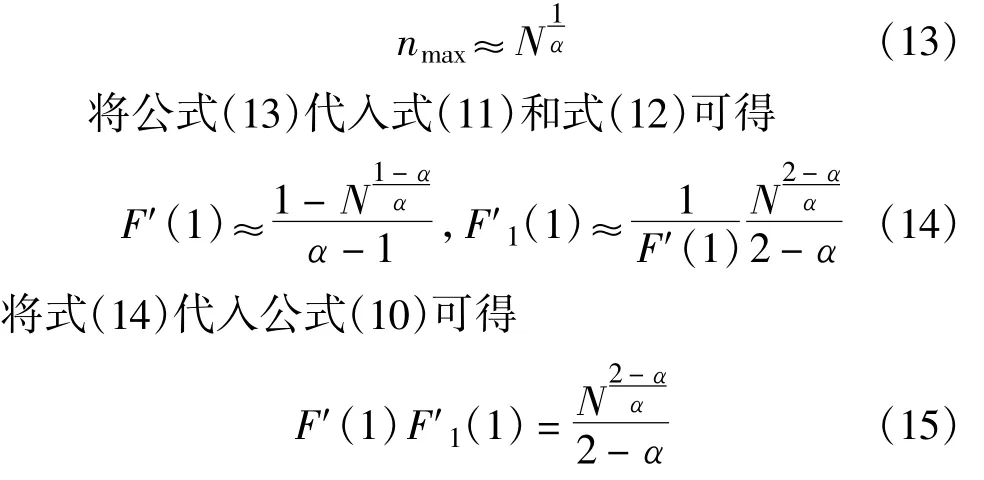
由上述分析可知，F′（1）与F′（1）F′1（1）分别代表与指定节点相连的节点数量的平均度，令

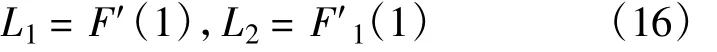
以此类推第i层节点数量的平均度记作Li，可以得到

根据上述公式推导，下面我们来分析对等网络系统中任意两节点的最短路径长度。假定对等网络中存在两个节点a、b以及两节点间的最短路径长度s，可以看出s表示为节点a与b之间从第一层到第s层的层数，且是最短的。同时在对等网络系统中，节点与节点通过各种连接与多种层次连接的节点总数（包括直接或间接连接的）为（N-1），可以得出

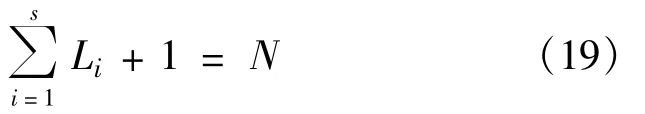
将公式（18）代入式（19），可以得出

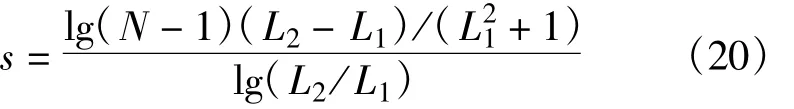
对于对等网络系统而言，节点的数量级别一般在104～105左右，因此节点的数量N≫L1、L2。这样公式（20）可以表示为

现在我们代入公式（14）与公式（16），可以得出对等网络系统中的节点最短路径长度：

由公式（22）可知：对等网络系统中，节点间的最短路径长度主要与这个网络系统的节点规模相关，对等网络系统的幂律指数不起主要作用。

4 仿真与讨论

本实验以典型的对等网络系统Gnutella为仿真场景，通过P2Psim软件建立Gnutella网络环境，分析对等网络节点行为的度分布、平均路径长度两种特征。设每个用户共享带宽为5 Mbit／s，定义系统中拥有节点用户数为50 000个，0≤n≤nmax（节点度大小为n的节点），s为对等网络中最小路径长度。

（1）节点度分布与节点数量的关系

根据公式（1）与公式（2）分别对应的随机网络模型和无标度网络模型对应的节点度计算方法，分别与节点实际的度分布数据进行对比，如图1所示，可以看出，无标度网络模型的度分布计算方法得出的数据更加接近实际的度分布，这与第三节的理论分析基本吻合。

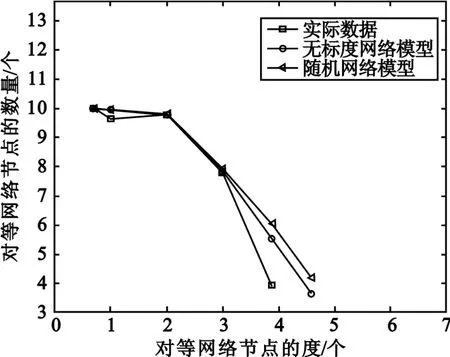
图1 节点度分布与节点数量的关系Fig.1 The relationship between the degree distribution of peers and the number of peers

（2）节点间的最短路径分析

在本文第3节我们提到，无标度网络模型更加适合用来分析对等网络系统节点的行为分析，因此这里我们基于P2Psim软件运行的数据，将实验结果的理论数据（即公式（22）所反映的最短路径计算方法）与实际数据通过Pajek软件［9］进行分析，比较结果如表1所示。可以看出，我们在节点规模控制在12 500、25 000、37 500、50 000分别进行分析，实际数据与无标度网络模型的最短路径长度误差基本控制在10%左右（这里是对所有节点最短路径取了平均值，因此精确到小数点后3位）；由于复杂网络系统的小世界特性，最短路径长度一般不会超过7，因此误差在10%完全可以忽略。同时我们可以看到，理论分析数据与实际数据存在一定的差异性。产生该差异的原因主要包括两点：首先，是我们在进行理论分析的过程中，为了讨论的连续性，对数据进行了近似处理，如公式（14）和公式（21）的近似处理；其次，我们在实际数据收集的过程中，存在许多不确定因素，如仿真环境、网络带宽、仿真主机的数据处理能力等。上述两点因素的相互影响，分别对理论数据和实际数据产生了一定的影响，就对等网络仿真实验的结果而言，误差范围控制在±15%内都可以接受，显然这里的数据对比结果完全可以满足仿真实验的要求。因此，本文第三节给出的对等网络系统中节点间最短路径的理论分析具有一定的正确性和合理性。

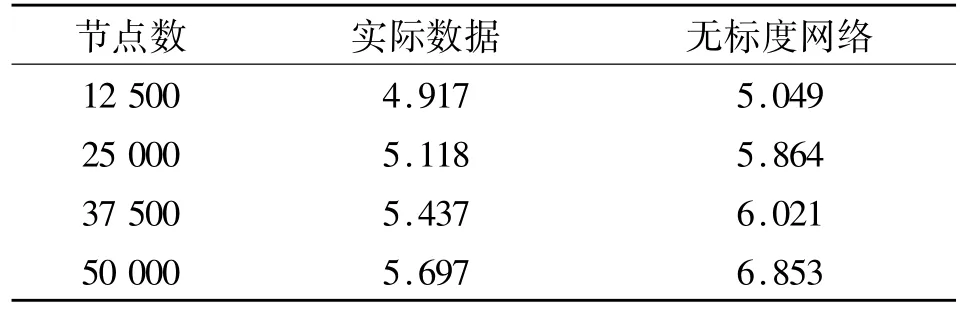
表1 实验数据与模型数据比较Table 1 Comparison between experimental data and model data

5 结论

本文基于复杂网络理论，对对等网络中网络行为的特征进行了深入分析。这些特征主要包括节点的度、平均路径长度等衡量参数，这些参数作为对等网络的重要特征量，直接关系到诸如对等网络系统路由、拓扑结构等性能的优化和改进。实验结果表明，本文给出的特征分析结果具有一定的合理性，能很好地体现对等网络的节点行为特征。然而，对于类似P2P网络这样的复杂网络，还需结合具体的网络架构进行特征分析，从而丰富本文的理论，更好地描述对等网络的节点行为特征，这将是下一步的研究重点。

［1］Newman M E J.The Structure and Function of Complex Net -works［J］.SIAM Review，2003，45（2）：167-256.

［2］Ravoaja Aina，Anceaume Emmanuelle.STORM：A Secure Overlay for P2PReputation Management［C］／／Proceedings of the First InternationalConference on Self-Adaptiveand Self-Organizing Systems.Boston，Mass，USA：IEEE，2007：247-256.

［3］Feng Qinyuan，Wu Yu，Sun Yan，etal.User BehaviorModeling in Peer-to-Peer File Sharing Networks：Dissecting Download and Removal Actions［C］／／Proceedings of 2009 IEEE International Conference on Acoustics，Speechand Signal Processing.Taipei，China：IEEE，2009：3477-3480.

［4］Wang X，Chen G.Synchronization in scale-free dynamical networks：robustness and fragility［J］.IEEE Transactions on Circuits and Systems，2002，49（1）：54-61.

［5］Li Xiang，Chen Guan-rong.A local-world evolving networkmodel［J］.Physical A，2003，328（1／2）：274-279.

［6］汪小帆，李翔，陈关荣.复杂网络理论与及其应用［M］.北京：清华大学出版社，2005：9-33. WANG Xiao-fan，LI Xiang，CHEN Guan-rong.Complex network theory and its application［M］.Beijing：Tsinghua University Press，2005：9-33.（in Chinese）

［7］Watts D.有序与无序之间的网络动力学［M］.陈禹，译.北京：中国人民大学出版社，2006：114-132. Watts D.Network dynamics between order and disorder［M］. Translated by CHEN Yu.Beijing：Renmin University of China Press，2006：114-132.（in Chinese）

［8］Watts D J，Strogatz S H.Collective dynamics of‘small world’networks［J］.Nature，1998（393）：440-442.

［9］Batagelj V，Mrvar A.Pajek-analysis and visualization of large networks［C］／／Processing of Graph Drawing Software. Springer，Berlin：IEEE，2003：77-103.

PENG Hao was born in Taixing，Jiangsu Province，in 1982.He received the M.S.degree in 2007.He is currently working toward the Ph.D.degree.His research concerns network security，computer communication networks.

Email：penghao2007＠sjtu.edu.cn

陆松年（1947—），男，上海人，1982年获学士学位，现为教授、博士生导师，主要研究方向为计算机通信网、信息保密与安全；

LU Song-nian was born in Shanghai，in 1947.He received the B.S.degree in 1982.He isnow a professor and also the Ph.D. supervisor.His research concerns computer communication networks，information secracy and security.

Email：snlu＠sjtu.edu.cn

赵丹丹（1981—），女，浙江台州人，2007年获硕士学位，现为博士研究生，主要研究方向为信息安全、视频编解码技术；

ZHAO Dan-dan was born in Taizhou，Zhejiang Province，in 1981.She received the M.S.degree in 2007.She is currently working toward the Ph.D.degree.Her research concerns information security and video codec technology.

Email：zhaodandan＠sjtu.edu.cn

李生红（1971—），男，辽宁葫芦岛人，1999年获博士学位，现为教授、博士生导师，主要研究方向为信息安全、信号与信息处理；

LISheng-hong was born in Huludao，Liaoning Province，in 1971.He received the Ph.D.degree in 1999.He is now a professor and also the Ph.D.supervisor.His research concerns information security，signal and information processing.

Email：shli＠sjtu.edu.cn

张爱新（1973—），女，上海人，2003年获博士学位，现为副研究员、硕士生导师，主要研究方向为信息安全、密码协议、多媒体信息处理及内容安全。

ZHANG Ai-xin was born in Shanghai，in 1973.She received the Ph.D.degree in 2003.She is now an associate research fellow and also the instructor of graduate students.Her research concerns information security，cryptographic protocols，multimedia information processing，and content security.

Email：axzhang＠sjtu.edu.cn

Application of Com plex Network Theory in Characteristics Analysis of Peer to Peer Networks

PENGHao1，LU Song-nian1，2，ZHAO Dan-dan1，LISheng-hong1，2，ZHANGAi-xin2
（1.Department of Electronic Engineering，Shanghai Jiaotong University，Shanghai200240，China；2.School of Information Security，Shanghai Jiaotong University，Shanghai200240，China）

According to the existing complex network theory，the complexity characteristics of peer to peer network are studied and then the achievement algorithm of two characteristic parameters including the degree of peers and the average shortest path between peers is designed and simulated.Simulation results show that the theoretical results using the analysis of the characteristics of the complex network theory are basically consistent with the experimental data results and the theoretical results can accurately reflect the characteristics of peer to peer network.

P2P（Peer to Peer networks）；complex network；the degree of a peer；the shortest path length

The National Program on key Basic Research Project（973 Program）（2010CB731403／2010CB731406）；The National Natural Science Foundation of China（No.61071152／61171173）

TP393.01

A

10.3969／j.issn.1001-893x.2012.04.030

彭浩（1982—），男，江苏泰兴人，2007年获硕士学位，现为博士研究生，主要研究方向为网络安全、计算机通信网；

1001-893X（2012）04-0571-05

2011-12-20；

2012-03-13

国家重点基础研究发展规划（973计划）项目（2010CB731403／2010CB731406）；国家自然科学基金资助项目（61071152／61171173）