一种低复杂度的MIMO-OFDM下行链路子载波分配改进算法✴

魏方旭，胡晓鹏

（西南交通大学信息科学与技术学院，成都610031）

一种低复杂度的MIMO-OFDM下行链路子载波分配改进算法✴

魏方旭，胡晓鹏

（西南交通大学信息科学与技术学院，成都610031）

针对多入多出正交频分复用（MIMO-OFDM）系统的下行链路，提出一种基于信道状态信息（CSI）反馈的次优子载波分配算法。算法从寻求容量和公平性之间的平衡出发，将提高系统容量作为资源分配的优化目标。该算法首先按照比例公平约束进行子载波初始分配，然后将现行分配给任意两个用户的子载波互换之后计算系统容量，如果系统容量增加，则将子载波在用户间进行交换，否则保持初始分配不变。将子载波在用户间进行迭代调整，直到系统总容量不再增加为止。仿真结果表明，该算法能够很好地保证比例公平约束，有效地提高系统容量，提升效率可以达到贪婪算法的40%左右，对MIMO-OFDM系统中的子载波分配具有一定的参考价值。

多入多出；正交频分复用；子载波分配；状态信息反馈；比例公平

1 引言

多入多出（MIMO）和正交频分复用（OFDM）被广泛地采用以提高频谱利用率，缓解频谱资源紧张的局面。MIMO和OFDM的应用使可分配的资源从时隙和频率扩展到时隙、频率和空间，大大增加了无线资源分配的灵活性，分配的复杂度也迅速增加，因此有必要研究有效的无线资源分配算法。

目前国内外已有很多针对多载波系统的动态无线资源分配的研究［1-9］。多用户OFDM的最优比特加载和子载波分配一般被表述为整数变量下的非线性优化问题［1］，该优化问题可以分为两类：一类是在满足用户速率要求和误码率（BER）的要求下使总体发送功率最小［2］；一类是在满足各用户速率要求和总功率约束的要求下使系统容量最大［3］。求解这类优化问题具有非常高的复杂度，大部分文献从不同角度给出了该优化问题的次优解。文献［3］表明，当每个子载波被分配给在该子载波上信道增益最好的用户且每个子载波在特定的时刻只能被一个用户占用时，OFDM系统的总数据速率能够最大化，但是用户间缺乏公平性。近年来，基于用户公平性的资源分配算法受到了广泛的关注［4-9］，这些算法使得可用资源在用户间较合理的分配，但是都有一定的局限，max-min无法处理不同速率比例的情况，文献［6-8］中的比例公平算法的系统容量不是最优的。

从满足比例公平的角度出发，以提高系统容量为目的，本文在文献［6-8］的基础上提出一种基于物理层CSI的MIMO-OFDM系统下行链路动态子载波分配的改进算法，通过子载波迭代交换，使每个子载波的传输能力在保证公平性的基础上得到充分利用，提高系统容量。

2 系统模型

MIMO-OFDM系统下行链路的系统框图如图1所示，基站发射天线数目为NT，每个用户的接收天线数为NR，假定NR＜NT，用户总数为K，子载波总数为N，基站端的总发射功率为Ptotal。另外，本文还采用了如下假设：无线信道具有时变慢衰落的特性；发射端具有理想的信道状态信息且能够及时更新信道状态信息；每个子载波在某一时刻只能被一个用户占用［10］。

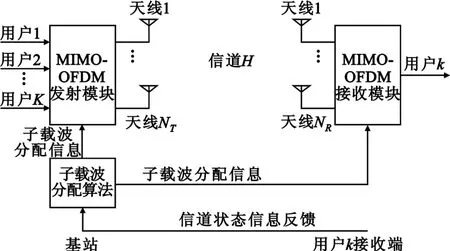
图1 MIMO-OFDM下行链路框图Fig.1 Block diagram of MIMO-OFDM downlink

图1 中每个用户的信道状态信息通过专用信道发送到基站端的子载波分配算法模块，该模块根据信道状态信息完成子载波分配，并将子载波分配信息告知接收端，然后MIMO-OFDM发射模块根据子载波分配信息在各个发射天线上产生OFDM符号，系统给每个OFDM符号添加循环前缀（CP）后将信号发送出去。在接收端，用户根据子载波分配信息来获取属于自己的信息。

MIMO传输信道一般采用NR×NT维的时变信道矩阵H（t）来描述［11］：

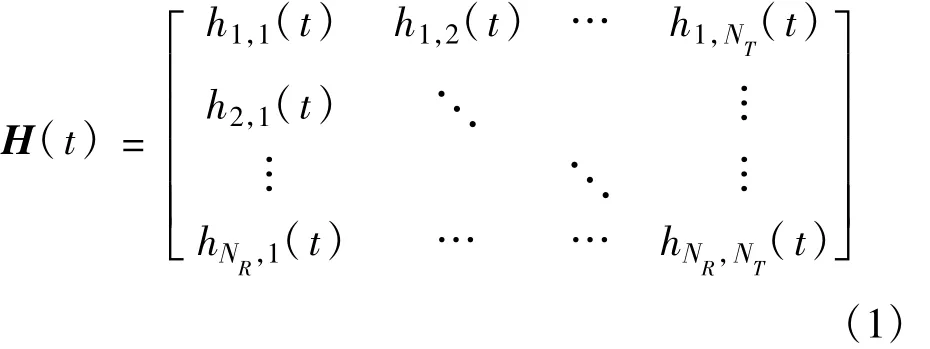
式中，hr，t（t）表示第t（t∈｛1，2，…，NT｝）个发射天线和第r（r∈｛1，2，…，NR｝）个接收天线间的信道转移函数。对式（1）进行奇异值分解（SVD），可将MIMO信道等效为多个并行的单输入单输出（SISO）信道，用户k在子载波n上可以获得的容量如式（2）所示［11］：

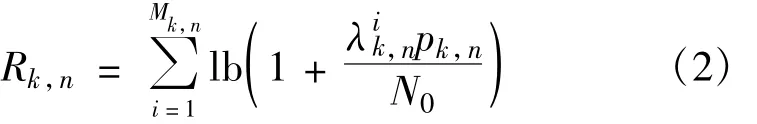
式中，λi

k，n是Hk，nHHk，n的第i个特征值，Mk，n表示Hk，n的秩，［·］H表示矩阵的共轭转置。

由式（2）不难得出，MIMO-OFDM系统容量最大的目标如式（3）所示［11］：

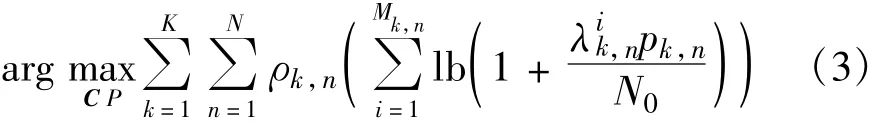
式中，C为K×N的子载波分配矩阵，ρk，n为矩阵C的元素，ρk，n=1表示子载波n分配给用户k，ρk，n= 0表示子载波n分配给其他用户；P为K×N的功率分配矩阵，pk，n为矩阵P的元素，表示用户k在子载波n分到的功率。式（3）应满足的总功率约束和比例公平约束由式（4）给出：

式中，｛γi｝Ki=1表示用户间的速率比率，用以确保用户间的公平性，用户k的容量Rk可由式（5）得到：

3 算法描述

对式（3）中的C和P同时进行求解就可以获得资源分配的最优解，但这是一个非线性的优化问题，求解过程具有很高的复杂度，而且基站必须在很短的时间内完成子载波和功率分配的计算才能满足无线信道快速变化的特点，因此非常有必要采用低复杂度的次优求解方法。将子载波分配与功率分配分开进行是一种降低算法复杂度的有效办法，因为目标函数中的变量能够减少一半［6］。文献［3］表明，在OFDM系统中采用最优功率分配方案与等功率分配方案所获得的性能相差不大，因此提出的算法在采用等功率分配的前提下进行子载波分配。为了保证用户间比例公平，优先选择公平因子Rk／γk较小的用户［7］，其中k∈｛1，2，…，K｝。算法的具体步骤如下。

（1）子载波初始分配

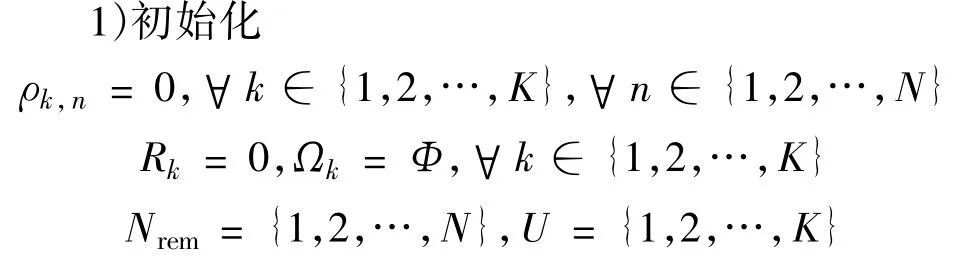
其中，Nrem表示可用子载波集，U表示需要分配子载波的用户集，Ωk表示分配给第k个用户的子载波集合。

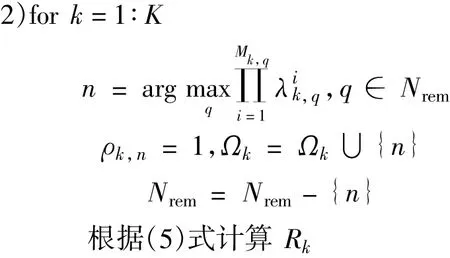
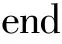
根据（5）式计算Rk

end

（2）迭代调整

子载波初始分配这一步确定了初始子载波分配矩阵，通过将子载波在不同的用户间交换［12］可以不断优化分配方案，交换的原则是使系统容量得到提高，满足这个条件的所有子载波必须完成交换：

1）对所有用户组合（i，j），i，j∈｛1，2，…，K｝且i≠j，计算容量增加因子ci，j。对暂时分配给用户i的子载波集Ωi中的每一个子载波n，计算如果将子载波n分配给用户j所获得容量变化Δci，j［n］= Cj，n-Ci，n，Ci，n表示用户i在子载波n上的容量，然后找出使Δci，j最大的子载波ni，j， 即

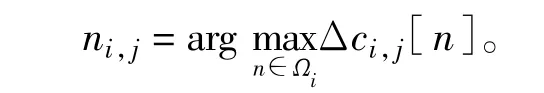
同样地，计算Δcj，i［n］并找到nj，i。如果将用户i的子载波ni，j与用户j的子载波nj，i交换，则用户组合（i，j）的容量增加因子ci，j=Δci，j［ni，j］+Δcj，i［nj，i］。

2）找到最大的容量增加因子c*i，j和相应的用户对（i*，j*），即

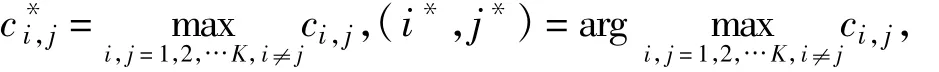
则用户对（i*，j*）可以交换的子载波为ni*，j*和nj*，i*。若c*i，j＞0，说明交换子载波ni*，j*和nj*，i*可使系统容量提高，因此将子载波ni*，j*和nj*，i*在用户对（i*，j*）间进行交换，将原来分配给用户i*的子载波ni*，j*分配给用户j*，原来分配给用户j*的子载波nj*，i*分配给用户i*，并更新子载波分配矩阵，然后返回到迭代调整的第一步；若c*i，j≤0，说明系统容量不可能再增加，整个分配过程结束。

4 仿真与分析

考虑单小区的下行链路，仿真中用到的频率选择性衰落信道采用具备6条多径的瑞利衰落信道模型，且服从指数衰落分布。用户数从2到16变化，信道状态每隔1ms更新一次，每次仿真的持续时间为20ms。

图2是不同算法在信噪比（SNR）为20 dB和采用4×2 MIMO时的容量比较，与文献［7］中的算法相比，当用户数为12时，贪婪算法［3］、本文算法和比例资源分配算法［8］的容量分别提高了1.89%、0.92%和0.51%；当用户数为16时，贪婪算法、本文算法和比例资源分配算法的容量分别提高了2.11%、0.90%和0.41%，本文算法的容量相比于文献［7］中的算法和比例资源分配算法得到了有效地提高。将文献［7］中的算法作为比较基础，本文算法的容量提升能够达到贪婪算法容量提升的40%左右。

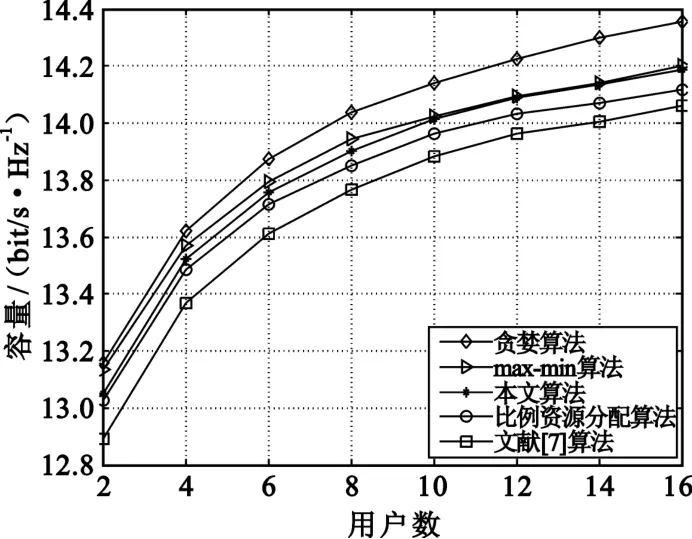
图2系统容量对比（4×2 MIMO）Fig.2 Comparison of system capacity（4×2 MIMO）

图3 是系统在SNR为20 dB和采用2×1 MIMO时的容量比较。图2和图3表明，在信号的带宽足够窄和信道的频率响应是准静态平坦衰落时，多天线的信道容量随天线个数的增加而线性增加［13］。

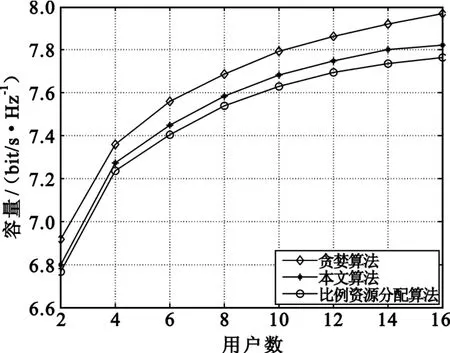
图3系统容量对比（2×1 MIMO）Fig.3 Comparison of system capacity（2×1 MIMO）

图4 是一次信道实现中用户数为16时算法的公平性性能比较，不难看出，本文算法能够很好地满足用户间的比例速率约束。

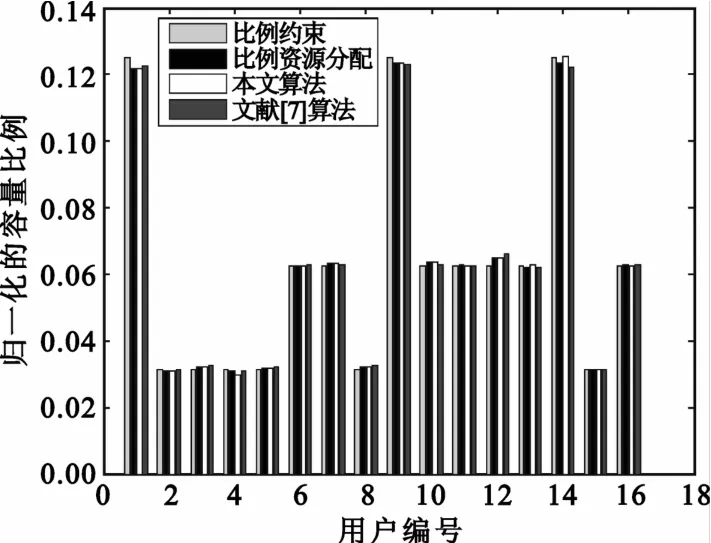
图4 用户的归一化容量Fig.4 Normalized capacity of users

文献［6］中定义的公平性参数可以更加准确地说明算法的比例公平性能，具体的定义如式（6）所示，该参数越小表明用户间的速率比例越接近比例约束，即能够更好地满足比例约束条件：

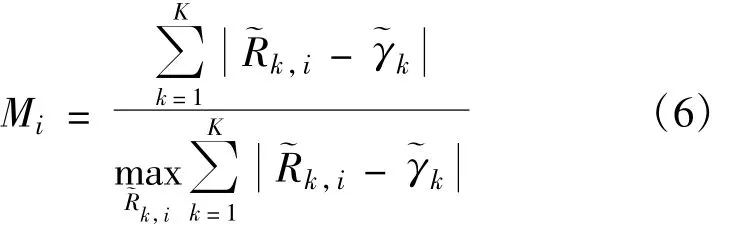
假设Rk，i是第i次信道实现中用户k的容量，则上式中分别表示用户k的归一化容量和归一化比例约束。式（6）中分母的计算方法如下：

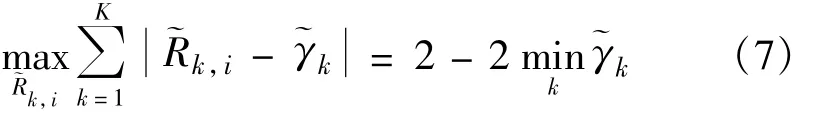
利用式（6）和式（7）计算本文算法、比例资源分配算法和文献［7］中算法的公平性参数分别为0.007 1、0.007 0和0.008 8，该结果表明本文算法的比例公平性与比例资源分配算法相比稍微有所下降，与文献［7］中算法相比有所提高，这与图4显示的结果是一致的。

贪婪算法不关注用户间的公平，能够获得较高的系统容量。文献［7］中算法信道条件差的用户组能够优先分配资源，导致这些资源的传输能力没有得到充分的利用，系统的总容量和比例公平性受到一定的影响。比例资源分配算法优先为公平因子Rk／γk较小的用户分配子载波，不会像文献［7］中算法那样明显歧视信道条件好的用户，因而信道容量和比例公平性相比文献［7］中算法有所提高。本文算法在比例资源分配算法的基础上，将已分配的子载波按照容量增加的原则在用户间迭代交换，导致原有的比例公平有所下降，但是每个子载波的传输能力得到了充分的利用，有效地提高了系统容量。max-min算法实际上是比例资源分配算法的一种特殊情况，只需让γ1∶γ2∶…∶γK=1∶1∶…∶1，比例资源分配算法就可以等同于max-min算法［6］。

以上仿真结果和分析表明，本文算法在保证比例公平性的前提下，与比例资源分配算法和文献［7］中算法相比具有更好的容量性能，虽然max-min算法与本文算法的容量性能相差不大，但是由于前者只能处理等速率比的情况，本文算法可以应付不同速率比的情况，因此算法具有更大的优势。

5 结束语

针对MIMO-OFDM系统的下行链路，本文提出了一种基于比例约束的子载波分配算法。为了减小复杂度，该算法采用次优求解，从仿真和分析中可以看出，与max-min算法、比例资源分配算法和文献［7］中的算法相比，本文算法具有较好的比例公平性，可用于比例公平约束可变的情况，同时能够有效地提高系统容量。本文算法对MIMO-OFDM系统的子载波分配具有一定的参考价值，但是算法没有考虑系统能效和多跳中继等因素，因此考虑能效和加入中继后系统的子载波分配可以作为进一步研究的方向。

［1］Inhyoung Kim，In-Soon Park，Yong H Lee.Use of Linear Programming for Dynamic Subcarrier and Bit Allocation in Multiuser OFDM［J］.IEEE Transactions on Vehicular Technology，2006，55（4）：107-116.

［2］Wong CY，Cheng RS，Letaief K B，etal.Murch.Multiuser OFDM with adaptive subcarrier，bit，and power allocation［J］.IEEE Journal on Selected Areas in Communication，1999，17（10）：1743-1758.

［3］JangJ，Lee K B.Transmit power adaptation for multiuser OFDM systems［J］.IEEE Journal on Selected Areas in Communication，2003，21（2）：171-178.

［4］RheeW，Cioffi JL.Increase in capacity ofmultiuser OFDM system using dynamic subchannel allocation［C］／／Proceedings of IEEE Vehicular Technology Conference.Tokyo：IEEE，2000：1085-1089.

［5］管张均，周希朗.基于容量最大化的多用户MIMO-OFDM子载波分配算法［J］.电讯技术，2011，51（9）：127-130. GUAN Zhang-jun，ZHOU Xi-lang.Subcarrier Allocation Algorithms for Multiuser MIMO-OFDM Systems Based on Maximum of Capacity［J］.Telecommunication Engineering，2011，51（9）：127-130.（in Chinese）

［6］SHEN Zu-kang，Andrews JG，Evans B L.Adaptive Resource Allocation in Multiuser OFDM Systems With Proportional Rate Constraints［J］.IEEE Transactions on Wireless Communications，2005，4（6）：2726-2737.

［7］Xu J，Kim JY，PaikW K，etal.Adaptive Resource Allocation Algorithm with Fairness for MIMO-OFDMA System［C］／／Proceedings of IEEE Vehicular Technology Conference.Melbourne：IEEE，2006：1585-1589.

［8］Wong IC，Shen Zukang，Evans B L，etal.A Low Complexity Algorithm for Proportional Resource Allocation in OFDMA Systems［C］／／Proceedings of IEEEWorkshop on Signal Processing Systems.Texas：IEEE，2004：1-6.

［9］Zhu Han，Zhu Ji，Liu K J R.Low-complexity OFDMA channel allocation with Nash bargaining solution fairness［C］／／Proceedings of IEEEGlobal Telecommunications Conference.Texas：IEEE，2004：3726-3731.

［10］LIHong-xiang，RUGuan-ying，Kim Younsun，etal.OFDMACapacity Analysis in MIMO Channels［J］.IEEE Transactions on Information Theory，2010，56（9）：4438-4446.

［11］AlbertMr′az，Tam′as Z′amb′o，S′andor Imre.Radio Resource Management for MIMO-OFDMA Access in Rayleigh Fading Channel［C］／／Proceedings of European Wireless Conference.Lucca：IEEE，2010：261-268.

［12］Cheong YuiWong，TsuiCY，Cheng R S，etal.A realtime sub-carrier allocation scheme for multiple access downlink OFDM transmission［C］／／Proceedings of IEEEVehicular Technology Conference.Amsterdam：IEEE，1999：1124-1128.

［13］刘辉，张复春，姜斌，等.频率选择性衰落MIMO信道容量分析［J］.电讯技术，2010，50（1）：15-20. LIU Hui，ZHANG Fu-chun，JIANG Bin，et al.Analysis of MIMO Channel Capacity under Frequency Selective Fading［J］.Telecommunication Engineering，2010，50（1）：15 -20.（in Chinese）

WEIFang-xu was born in Enshi，Hubei Province，in 1986. He received the B.S.degree form Qingdao Technological University in 2009.He is now a graduate student.His research direction is radio resourcemanagement.

Email：vifangxu＠gmail.com

胡晓鹏（1972—），男，陕西汉中人，1997年于西南交通大学获工学硕士学位，现为副教授、硕士生导师，主要研究方向为无线资源管理。

HU Xiao-peng was born in Hanzhong，Shaanxi Province，in 1972.He received the M.S.degree from Southwest Jiaotong University in 1997.He is now an associate professor and also the instructor ofgraduate students.His research direction is radio resource management.

An Im proved Sub-carriers Allocation Algorithm w ith Low Complexity for M IMO-OFDM Downlink

WEIFang-xu，HU Xiao-peng
（School of Information Science and Technology，Southwest Jiaotong University，Chengdu 610031，China）

A suboptimal sub-carriers allocation algorithm based on channel state information（CSI）for the downlink of Multiple Input Multiple Output-Orthogonal Frequency Division Multiplexing（MIMO-OFDM）system is proposed in this paper.The tradeoff between fairness and capacity is considered and the purpose of the algorithm is tomaximize the capacity of the system.The algorithm firstly implements initial allocation according to the proportional fairness constraint，and then calculates the variety of the system capacity if the sub-carriers allocated to any pair of the usersare swapped.If the system capacity is increased，the sub-carriersare swapped，or the initial allocation is kept.The sub-carriers among users are iteratively swapped until the system capacity couldn′t be improved.Simulation result shows that the proposed algorithm can improve system capacity effectively with proportional fairness among users and the capacity increment can reach about 40%of the greedy algorithm. The conclusion has reference value for the sub-carriers allocation in the MIMO-OFDM systems.

MIMO；OFDM；sub-carrier allocation；CSI feedback；proportional fairness

TN929.5

A

10.3969／j.issn.1001-893x.2012.04.026

魏方旭（1986—），男，湖北恩施人，2009年于青岛理工大学获工学学士学位，现为硕士研究生，主要研究方向为无线资源管理；

1001-893X（2012）04-0553-05

2011-11-25；

2012-02-20