LDPC 码的改进迭代比特翻转译码算法✴

刘原华，张美玲

（西安邮电学院通信与信息工程学院，西安710121）

LDPC 码的改进迭代比特翻转译码算法✴

刘原华，张美玲

（西安邮电学院通信与信息工程学院，西安710121）

为提高低密度奇偶校验（LDPC）码的低复杂度硬判决译码算法的性能，提出了一种改进的比特翻转（BF）译码算法，在迭代时利用一个交替的门限模式对多个比特进行翻转，降低了每次迭代时比特被错误翻转的概率，从而有效提高了译码性能。仿真结果表明，与BF算法相比，该算法在保持低复杂度的基础上获得了更好的译码性能和更快的收敛速度。

低密度奇偶校验码；比特翻转；迭代译码

1 引言

早在1962年，Gallager就提出了低密度奇偶校验码（LDPC码）［1］，但由于当时计算能力的限制该类码一直未得到重视，直到1996年，Mackay和Neal重新发现了LDPC码，指出其具有逼近Shannon限的纠错性能。近年来，LDPC码因其优异的纠错性能成为编码领域的研究热点，目前已广泛应用于深空通信、光纤通信和卫星数字视频广播等领域。

LDPC码最有效的译码算法是迭代置信传播（BP）译码，在迭代过程中传递的是概率消息，将接收比特信号的幅度表示成一定精度下的浮点数，迭代过程中通过进行大量的实数运算，可获得逼近Shannon限的性能，然而计算复杂度非常高。为降低计算复杂度，提出了很多替代算法，如最小和算法等，当然带来了性能上的一定损失。

LDPC码的另一种译码算法是Gallager提出的比特翻转（BF）算法［1］，其只涉及硬判决逻辑运算，而不考虑与接收比特信号的幅度有关的可靠性信息。若某一比特所参与的不满足的校验方程的个数超过某一固定的门限值时，将该比特进行翻转。尽管BF算法仅适用于信噪比较高的系统，但该算法简单快速且非常易于硬件实现，极有潜力应用于现代高速可靠的通信网络。BF算法复杂度非常低，但性能较差，为改善译码性能，文献［2］中提出了一种改进的BF算法，在每轮迭代中以一定的概率对部分不满足的比特进行翻转，而不是翻转所有不满足的比特，获得了性能的提高，但译码速度有所降低。为加快译码速度，在低复杂度的基础上获得良好的译码性能，有很多学者对各种改进BF算法［3-6］进行了深入研究，使LDPC码更适于实际应用。

在实时性要求较高的高速通信系统中，需要尽可能加快编译码速度，降低编译码复杂度。为了使LDPC码能够在保证一定纠错性能的基础上适于高速通信系统，本文提出了一种改进的BF算法，在迭代过程中利用一个交替变化的门限模式进行比特翻转，在低复杂度的基础上既改善了译码性能又提高了译码收敛速度。与BF算法相比，改进BF算法在复杂度不变的同时获得了更好的性能，非常适用于设计高吞吐量的硬件译码器。

2 BF算法

LDPC码由其稀疏的校验矩阵H所确定，若H的维数为M×N，且H的每一列均有γ个“1”，每一行均有ρ个“1”，其余元素均为“0”，则H的零空间即为码长为N的二进制规则LDPC码。

假设信道采用均值为0、方差为σ2=N0／2的加性高斯白噪声信道（AWGN），调制方式为二进制相移键控（BPSK）调制。二进制码字c=［c0，c1，…，cN-1］经调制后映射为序列x=［x0，x1，…，xN-1］，其中xn=1-2cn（0≤n≤N-1），信道的输出序列为r=［r0，r1，…，rN-1］，其中rn=xn+vn（0≤n≤N-1），vn为高斯噪声变量，接收序列r对应的硬判决序列为z=［z0，z1，…，zN-1］。

BF算法在每轮迭代中，首先根据上一轮的硬判决序列计算校正子的值。如果校正子为全0向量，则停止译码，并显示译码成功；否则对硬判决序列中的每一比特，计算其参与的不满足的校验方程的个数，即校正子中1的数目，记为fn，若fn超过某个预先设定的门限T，则对该码元比特zn进行翻转，从而得到一个新的硬判决序列。然后进入下一轮迭代，直至校正子为全0向量或者达到最大迭代次数。BF译码算法的具体步骤如下。

（3）重复执行第1步和第2步直至译码成功，或者达到最大迭代次数。

BF算法是一种硬判决译码算法，迭代过程中仅涉及逻辑运算，实现非常简单。虽然BF算法只在高信噪比时具有好的性能，但非常有潜力应用于功率有限的移动通信或者超高速通信网络。

3 改进BF算法

为了降低译码实现复杂度，提高译码速度，使LDPC码适合于高速通信系统，本文提出了一种改进的BF算法，在迭代过程中利用一个交替的门限模式来判定是否对比特进行翻转，改进算法的译码复杂度与BF算法一样低，只涉及逻辑运算，可实现快速有效的译码。

BF算法所依据的本质思想是，对每一码元比特来说，参与的不满足的校验方程越多，则该码元比特出错的可能性就越大。最佳门限T的选择不仅取决于校验矩阵的结构参数，同时还取决于信噪比的大小以及错误比特的数目。如果门限T取得太小，则将导致很多正确的比特被错误地翻转，致使译码无法向正确码字收敛。另一方面，门限T必须选取得足够小，才能使参与较少不满足的校验方程的错误比特能够被正确翻转。反之，如果门限T取得太大，则将会使译码向正确码字收敛速度减慢，并有可能陷入死循环使得某些错误比特无法翻转。

基于以上分析，本文提出一种可有效利用门限提高纠错性能的改进BF译码算法。首先给出翻转门限模式的概念。基于BF算法，将第1次迭代、第2次迭代、第3次迭代…使用的翻转门限值组成的序列T1-T2-T3-…定义为翻转门限模式。若门限模式的长度小于所需要的迭代次数，则重复使用该门限模式进行迭代译码。例如，若翻转门限模式为T1-T2，则在迭代过程中，奇数次迭代以T1作为门限，偶数次迭代以T2作为门限。由上述分析可知，通过对门限模式的精心选取，在迭代过程中可有效降低比特被错误翻转的概率，从而提高纠错性能。

以LDPC码（1008，3，6）为例，每一码元比特参与3个校验方程，翻转门限应该选为3或2。在前几次迭代时，错误比特较多，应该选择较大的值3作为门限，当错误比特的数目降低到一定程度时，门限应降为2，用来翻转参与大于等于2个不满足校验方程的比特。由于门限低，很有可能会使码元比特的出错率增大，此时应将门限增大为3来纠正错误的比特以降低错误比特的数目。如此交替使用3和2作为门限值直至达到最大迭代次数可有效提高纠错性能。最佳门限模式的确定可通过仿真来实现，以达到最佳的纠错性能。

改进BF算法的具体步骤如下：

（1）由硬判决z根据式（1）计算校正子s=［s0，s1，…，sM-1］，如果s=0，则停止迭代；否则执行第2步；

（2）第i次迭代时，对于每一硬判决比特zn，根据式（2）计算其参与的不满足的校验方程的个数fn，如果fn≥Ti，则翻转zn；

（3）重复第1步和第2步直至校正子为全0向量，或者达到预先设定的最大迭代次数。

由上述译码步骤容易看出，改进BF算法与BF算法的计算复杂度相同，每轮迭代时仅需要逻辑运算，实现非常简单，可以节省大量的能量以及硬件空间。理论分析表明，改进BF算法可通过优化门限模式有效降低比特被错误翻转的概率，从而获得纠错性能的提高。需要指出的是，若LDPC码校验矩阵的列重较小，则改进BF算法能够很容易通过仿真选取最佳的门限模式。而当LDPC码校验矩阵的列重较大时，最佳门限模式的选取变得稍微复杂，主要原因是此时所能够选择的门限模式较多。众所周知，LDPC码是以其校验矩阵的稀疏性得名，其校验矩阵中非零元素极少，并且校验矩阵的行重要大于列重，所以一般情况下校验矩阵的列重均比较小。另外，门限模式的选取是在迭代译码开始之前进行，门限模式一旦确定，在译码的迭代过程中无需变更，每轮迭代的复杂度不会增加，这意味着即使门限模式的选取稍微复杂，也并不会影响译码算法的整体复杂度。

4 仿真结果

图1给出了LDPC码（1008，3，6）在BF算法和改进BF算法下的误比特率（BER）性能曲线。BF算法的最大迭代次数设为50，改进BF算法的最大迭代次数分别设为2、4、6、10和50。如图1所示，在BER为10-5时，与BF算法（门限模式为3）相比，通过交替使用门限3和2，改进BF算法（门限模式为3-2）获得了大约2.5 dB的编码增益。

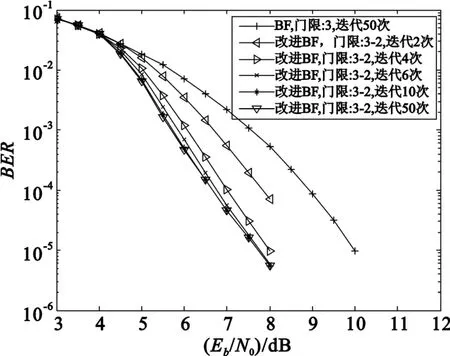
图1 LDPC码（1008，3，6）在BF算法和改进BF算法下的性能Fig.1 Performance of LDPC code（1008，3，6）with BF and the improved BF algorithms

由图1可以看出，在门限模式3-2下，改进BF算法在迭代10次以内时可有效改善译码性能，迭代10次后再增加迭代次数所获得的编码增益变得非常有限，迭代10次获得的性能与迭代50次获得的性能几乎相同，这意味着改进BF算法具有较快的译码收敛速度，迭代10次后即可达到近似最佳的性能。由此可以看出，最大迭代次数选择为10次，可实现译码性能和计算复杂度之间的良好折衷。

图2给出了LDPC码（2550，4，10）在BF算法和改进BF算法下的BER性能曲线。BF算法的最大迭代次数设为50，改进BF算法的最大迭代次数设为10。如图2所示，在BER为10-5时，与BF算法（门限模式为3）相比，改进BF算法（门限模式为4-3-2）获得了0.7 dB的编码增益。

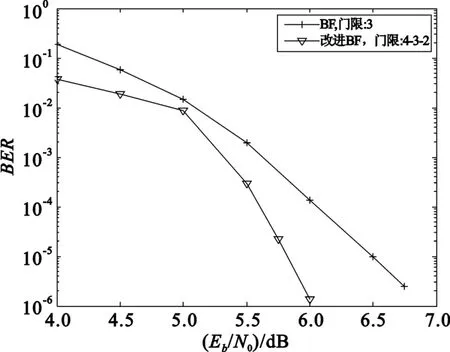
图2 LDPC码（2550，4，10）在BF算法和改进BF算法下的性能Fig.2 Performance of LDPC code（2550，4，10）with BF and the improved BF algorithms

5 结束语

本文研究了LDPC码的硬判决BF译码算法，发现通过适当地选取译码门限，可以有效提高BF算法的性能。由此，提出了一种改进的BF算法，在迭代过程中不是使用一个固定的门限而是利用一个交替的门限模式进行比特翻转，降低了错误翻转的概率，提高了译码性能。仿真结果表明，与标准的BF算法相比，改进BF算法以同样低的复杂度获得了更优的译码性能，同时改进BF算法仅需要较少的迭代次数即可收敛，有效降低了译码延时和计算复杂度，非常适用于功率有限的移动通信系统或者实时性要求较高的高速通信网络。

本文主要是对LDPC码硬判决译码进行研究，为保证复杂度低并未利用信道的软信息，下一步将分析如何在尽量低的复杂度下利用信道的软信息进一步提高硬判决译码的性能。

［1］Gallager R G.Low density parity check codes［J］.IEEE Transactions on Information Theory，1962，8（1）：21-28.

［2］Miladinovic N，FossorierM.Improved bit-flipping decoding of low-density parity-check codes［J］.IEEE Transactions on Information Theory，2005，51（4）：1594-1606.

［3］Ngatched TM N，Bossert M，Fahrner A，et al.Two bitflipping decoding algorithms for low-density parity-check codes［J］.IEEE Transactions on Communications，2009，57（3）：591-596.

［4］Dong JQ，Li Y N，Xie N D，et al.Candidate bit based bit -flipping decoding algorithm for LDPC codes［C］／／Proceedings of 2009 IEEE International Symposium on Inforamtion Theory.Seoul，Korea：IEEE，2009：2166-2168.

［5］Hung JH，Chen SG.A 16Gbps real-time BF-based LDPC decoder for IEEE 802.3an standard［C］／／Proceedings of 2011 International Conference on Multimedia and Signal Processing.Guilin，China：IEEE，2011：63-67.

［6］Cho J，Kim J，Sung W.VLSI implementation of a highthroughput soft-bit-flipping decoder for geometric LDPC codes［J］.IEEE Transactions on Circuits and Systems I，2010，57（5）：1083-1094.

LIU Yuan-hua was born in Xuzhou，Jiangsu Province，in 1983.She received the Ph.D.degree from Xidian University in 2010.She is now a lecturer.Her research concerns channel coding and modulation technology.

Email：yuanhliu＠163.com

张美玲（1982—），女，广东梅州人，2010年于西安电子科技大学获博士学位，现为西安邮电学院讲师，主要从事信息安全方面的研究。

ZHANGMei-lingwasborn in Meizhou，Guangdong Province，in 1982.She received the Ph.D.degree from Xidian University in 2010. She is now a lecturer.Her research concerns information security.

An Im proved Iterative Bit-flipping Decoding Algorithm for Low-density Parity-check Codes

LIU Yuan-hua，ZHANGMei-ling
（School of Communication and Information Engineering，Xi′an University of Posts and Telecommunications，Xi′an，710121，China）

An improved iterative bit-flipping（BF）algorithm adapted for decoding low-density parity-check（LDPC）codes is proposed to improve the performance of the hard-decision BF decoding algorithm.The new algorithm usesan alternating threshold pattern to determine the bitswhether to be flipped or not，and the flipping error probability is effectively decreased.Simulation results show that compared with BF algorithm，the improved BF algorithm improves both the error-correction performance and the convergence speed whilemaintaining the low computational complexity.

low-density parity-check code；bit-flipping；iterative decoding

The National Program on Key Basic Research Project（973 Program）（2012CB328300）；The Scientific Research Program Funded by Shaanxi Provincial Education Department（11JK1007）；The Program for Young Teachers in Xi′an University of Posts and Telecommunications（No.0001286）

TN911.21

A

10.3969／j.issn.1001-893x.2012.04.013

刘原华（1983—），女，江苏徐州人，2010年于西安电子科技大学获博士学位，现为西安邮电学院讲师，主要从事信道编码、通信调制方面的研究；

1001-893X（2012）04-0488-04

2011-11-15；

2012-02-17

国家重点基础研究发展规划（973计划）项目（2012CB328300）；陕西省教育厅专项科研计划项目（11JK1007）；西安邮电学院青年教师基金项目（0001286）