一种高效的TD-LTE系统频偏估计改进算法✴

陈发堂，滕旺，李小文

（重庆邮电大学重庆市移动通信重点实验室，重庆400065）

一种高效的TD-LTE系统频偏估计改进算法✴

陈发堂，滕旺，李小文

（重庆邮电大学重庆市移动通信重点实验室，重庆400065）

鉴于TD-LTE系统下行同步过程中频偏估计模块的重要性，提出了一种利用旋转因子校正的改进方法，在时域联合估计小数频偏和整数频偏，对接收信号在有限频偏范围内进行频偏补偿后做相关，根据相关能量峰值确定频偏大小。仿真结果表明，该算法无论是在可靠性还是在复杂度的降低上较常规算法都有很大提高，具有一定的参考价值。

TD-LTE；正交频分复用；频偏估计；相关；旋转因子

1 引言

由于具有高频谱效率、抗多径信道和支持宽带传输等优点，正交频分复用（Orthogonal Frequency Di

vision Multiplexing，OFDM）技术已经广泛应用于诸如WLAN、WiMAX以及数字广播技术（DVB）等无线通信系统中，并已成为3GPP长期演进（Long Term Evolution，LTE）及4G标准LTE-advanced中的核心技术。但其也存在着许多缺点，其中较为代表性的就是易受频率偏差的影响。载波频率偏差主要由两方面原因造成：发射机和接收机的本地振荡器频率存在误差和多普勒频移。频偏的存在使得系统的误码率迅速恶化，为此，很多频偏估计的算法相继被提出，大致可以分为3类：基于数据辅助［1-2］、半盲估计［3］及盲估计［4-5］算法。典型的有基于训练序列的估计算法［6］和基于循环前缀（CP）的大似然估计算法［7］，我们简记为算法1和算法2。

算法1在频域或时域插入导频序列，通过时域互相关算法估计小数频偏。该算法计算复杂度适中，但因估计函数限制，在整数频偏存在情况下不能正确估计小数频偏；其次，该算法依赖可靠定时同步，当信道环境恶劣或定时同步偏差较大，性能会严重下降。

算法2利用CP的重复结构特点来进行自相关运算。文献［7］将接收信号的CP与其延时一个OFDM符号长度的数据进行相关，根据最大似然函数值确定每个OFDM符号的起始位置和小数倍频偏。该算法计算复杂度较高，在多径信道下，存在多径时延，循环前缀已受前一个符号时延的干扰，估计性能很差。

整数倍频偏估计通常在频域进行，根据其对信号造成的载波整体偏移特点，采用互相关算法，寻找相关峰值距离中心频点偏移量来得到。但在定时误差存在情况下，引入的相位旋转因子将会影响训练序列的相关，易出现误判。针对此情况，文献［8］提出一种基于频域的差分互相关算法，利用频域前后信号的差分关系来消除定时偏差引入的影响，该算法对抗定时偏差有一定改良，但其性能有限，复杂度也较常规互相关算法高。

鉴于以上分析，本文在考虑算法复杂度以及对抗定时偏差性能的基础上提出了不同的频偏估计改进算法。

2 基于旋转因子校正的改进算法

自动频率控制法［9］的基本原理如下：在TDDLTE系统中，主同步信号的时域复数序列为｛ak｝，1≤k≤2 048。假设存在频偏和信道噪声，则接收端时域信号可表示为

式中，n（k）表示噪声，Δf表示频率偏移，T表示OFDM符号周期，N为数据长度，exp（j2πΔfkT）为载波频偏引入的旋转因子。将接收的主同步信号与发送的主同步信号进行共轭乘得到

由于a*kak为定值，因此上式可化简为

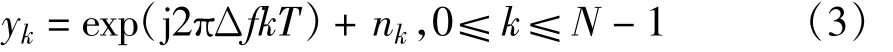
从而得到载波频偏Δf的似然函数

其中，使似然函数最大的就是最大似然估计值。由算式可知无法得到闭环解，因此它的精确估计就需使用离散数值计算方法实现。

在LTE系统中，一般整数倍频偏大致在2～3个载波间隔内，小数倍频偏在0.5个子载波间隔内，鉴于有限的载波频偏，可以考虑采用上面的算法在时域联合估计小数倍和整数倍频偏。假设发送端信号为ak，接收端信号为

其中，ε=εI+εF，εI为归一化整数倍频偏，εF为归一化小数倍频偏，在这里我们先不考虑信道噪声影响，简要流程如图1所示。

图1 频偏估计算法框图Fig.1 Block diagram of frequency offset estimation algorithm

具体步骤如下。

首先，对接收信号在载波区间［-εIMAX，εIMAX］内进行旋转因子校正，εIMAX为最大载波偏移，则yk（n）=rkexp（j2πkεnT），其中εn为步长间隔。

然后与本地信号ak做共轭相关，求得相关能量值为E，当能量值最大时，相应的校正量εn即为所估计的粗频偏，此时载波频偏被固定在一个区间内。由于校正量的大小影响到估计频偏的精度，因此对接收信号进行频偏校正后再次进行频偏精同步。此时缩小估计范围和校正量εn，重复上述步骤，即得到剩余频偏估计值。

从上面的步骤中可以看出，该算法的估计精度和校正量有关，校正量越小，估计精度越高，但以增加算法复杂度为代价。为此，可以减小相关运算量来降低整个算法流程的复杂度。具体如下：在计算能量值之前对本地信号及校正后信号进行32或64倍降采样，使相关点数成倍下降。仿真结果表明该算法性能在降采样很大时仍有较好性能，而常规算法如采用高倍降采样，其性能很差。为此，可以利用新算法的优势来弥补校正量减小所带来的计算复杂度。

3 仿真结果及分析

为了对比不同算法的性能，在本节中，我们根据各种算法的理论推导，在MATLAB环境对不同条件下不同算法进行仿真，具体仿真参数如表1所示。

表1 主要仿真参数Tabe 1 Major simulation parameters

图2～4仿真了3种小数频偏估计算法在不同信道下性能，归一化小数频偏为0.3。

图2为EPA5Hz步行信道下的仿真结果，由图可知在多径信道下，尤其是当信噪比较低时，基于CP的ML算法性能要比常规基于PSS的算法性能差很多，因为多径时延已经干扰到循环前缀的数据。

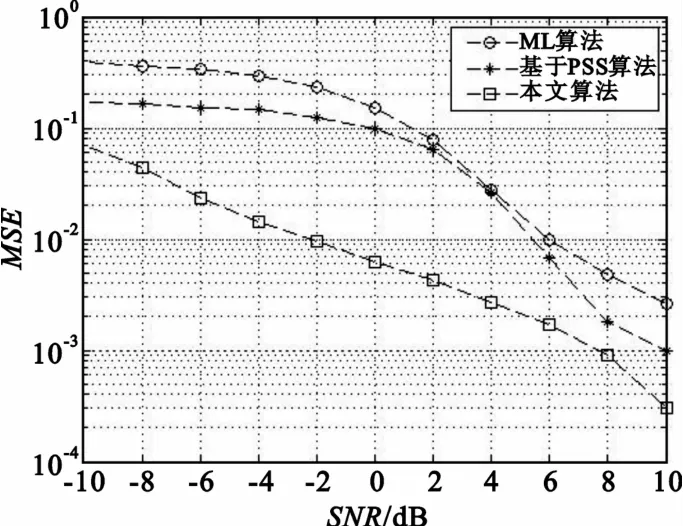
图2 EPA5Hz信道下3种算法性能Fig.2 Performance of three algorithms under EPA5Hz channel

图3 为高斯白噪声信道下的仿真结果，由图可知在高斯白噪声信道下，基于CP的ML算法性能非常好，已经符合一般通信系统的对频偏的要求，但本文的算法可以将频偏近似归零化，性能较ML算法更好。

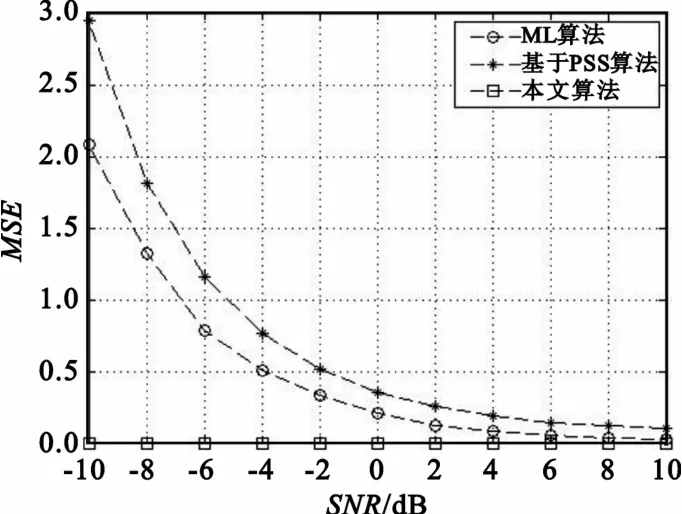
图3 AWGN信道下3种算法性能Fig.3 Performance of three algorithms under AWGN channel

图4 为ETU300Hz信道下的仿真结果，由图可知在该信道下，ML算法的劣势完全体现了出来，而本文提出的算法性能仍然较常规两种算法好。

图4 ETU300Hz信道下3种算法性能Fig.4 Performance of three algorithms under ETU300Hz channel

图5 为高斯白噪声信道及EPA5Hz步行信道下基于旋转因子校正算法在不同步长下小数倍频偏估计的性能，仿真结果表明在多径信道下随着步长的减小，该算法估计小数倍频偏的性能及精度都会提高，但是以增加计算复杂度为代价，因而在进行小数倍频偏精估计时，需要综合考虑这两种因素以权衡。

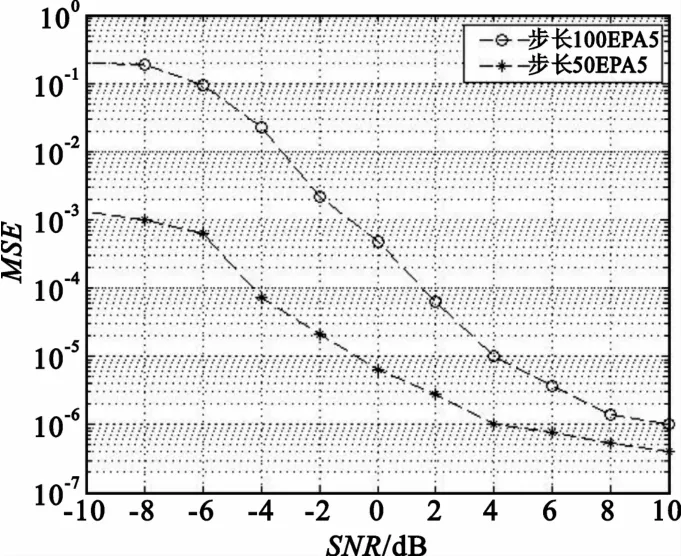
图5不同步长时的性能Fig.5 Performance under different step

图6 ～11主要仿真整数倍频偏估计各种算法的性能，其中下行带宽为10个RB，因此中心频点为29的位置，仿真中归一化整数倍频偏大小为2，定时偏差分别为0和20。

图6和图7为常规算法的仿真结果，在频域根据相关峰值点距离中心频点的偏移量来估计整数倍频偏大小，时偏为0时，该算法能够正确估计出整数倍频偏，但当存在定时偏差20个点时，由于定时偏差引起的相位旋转因子降低了PSS互相关的性能，因此整数倍频偏大小的估计会出现较大的误判。

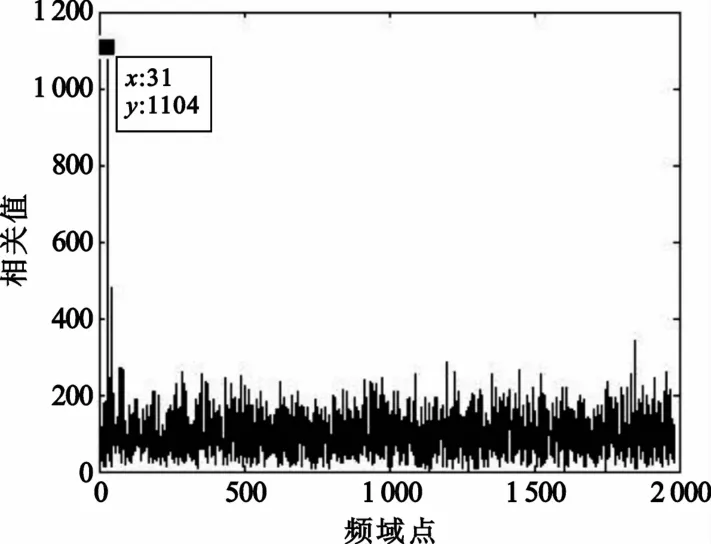
图6 时偏0情况下常规算法估计整数倍频偏性能Fig.6 Performance of estimator IFO of normal algorithm with no time error

图7时偏20情况下常规算法估计整数倍频偏性能Fig.7 Performance of estimator IFO of normal algorithm with 20 time error

图8 和图9为差分法估计整数倍频偏的仿真结果，可见该算法通过差分相关消除定时偏差引入的相位旋转因子，能够有效对抗时偏，但差分相关增大了算法的复杂度。

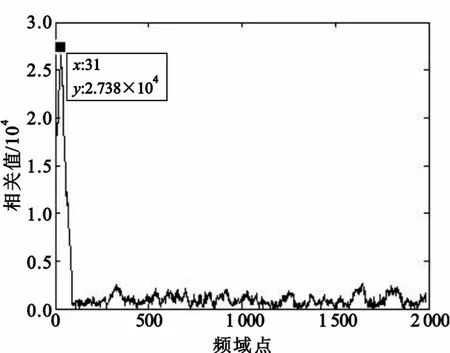
图8 时偏0情况下差分算法估计整数倍频偏性能Fig.8 Performance of estimator IFO of differential algorithm with no time error

图9时偏20情况下差分算法估计整数倍频偏性能Fig.9 Performance of estimator IFO of differential algorithm with 20 time error

图10 和图11为本文算法估计整数倍频偏的仿真结果，考虑到时偏以及算法复杂度的大小，改进的算法通过在时域基于旋转因子校正来估计整数倍频偏，结果表明该算法能够有效对抗定时偏差，同时省去了FFT变换从而极大地减小了运算量。

图10 时偏0情况下本文算法估计整数倍频偏性能Fig.10 Performance of estimator IFO of proposed algorithm with no time error

图11 时偏20情况下本文算法估计整数倍频偏性能Fig.11 Performance of estimator IFO of proposed algorithm with 20 time error

表2给出3种整数倍频偏算法的计算复杂度，可见改进的算法在复杂度上远小于当前多数文献提出的算法，原因在于本文提出的算法在时域联合估计小数和整数频偏，避免FFT变换，极大减小了运算量。

表2 整数倍频偏估计复杂度Tabe 2 Complexity of IFO estimation

4 结束语

本文提出了一种有效估计载波频偏的算法，在基于旋转因子校正算法估计小数倍频偏的基础上进一步改进，用来在时域联合估计整数倍和小数倍频偏。从理论上简要分析了当前各种频偏估计算法的原理，针对多种无线信道对算法性能和运算复杂度进行了对比，结果表明该算法性能良好，估计小数倍频偏的均方误差在一般无线通信系统允许范围内，能有效对抗多径信道以及由不准确定时同步算法引入的定时偏差。

［1］Awoseyila A B，Kasparis C.Improved Preamble-Aided Timing Estimation for OFDM System［J］.IEEE Communications Letters，2008，12（11）：825-826.

［2］Schmidl TM，Cox D C.Robust frequency and timing synchronization for OFDM［J］.IEEE Transactions on Communications，1997，45（12）：1613-1621.

［3］Jan-Jaap van de Beek，Magnus Sandell.ML Estimation of Time and Frequency Offset in OFDM［J］.IEEE System Signal Processing，1997，45（7）：1800-1805.

［4］ChinWen-Long，Chen Sau-Gee.A Blind Synchronizer for OFDM Systems Based on SINR Maximization in Multipath Fading Channels［J］.IEEE Transactions on Vehicular Technology，2009，58（2）：625-635.

［5］Mo Ronghong，Chew Yong Huat，Tjhung Thiang.A New Blind Joint Timing and Frequency Offset Estimator for OFDM Systems OverMultipath Fadding Channels［J］.IEEETransactions on Vehicular Technology，2008，57（5）：2947-2957.

［6］盛渊，罗新明.LTE中小区搜索算法的研究［J］.通信技术，2009，42（3）：90-92. SHENG Yuan，LUO Xin-min.Algorithm Study on Cell Search in LTE［J］.Communications Technology，2009，42（3）：90-92.（in Chinese）

［7］Lee J，Lou H，Toumpakaris D.Maximum likelihood estimation of time and frequency offset for OFDM systems［J］.Electronics Letters，2004，40（22）：1662-1663.

［8］侯华俊，吴斌，黑勇.高精度OFDM整数倍频偏与符号同步频域联合估计算法［J］.现代电子技术，2009，43（13）：93-96. HOU Hua-jun，WU Bin，HEIYong.Precise Frequency-Domain Joint Estimation of Integer Carrier Frequency Offset and Symbol Synchronization［J］.Morden Electronic Technology，2009，43（13）：93-96.（in Chinese）

［9］陈发堂，郑建宏，申敏，等.一种自动频率控制方法：中国，ZL200310110835.4［P］.2005-05-04. CHEN Fa-tang，ZHEN Jian-hong，SHEN Min，et al.A method of auto-control Frequency：China，ZL20031-0110835.4［P］.（2003-10）.（in Chinese）

CHEN Fa-tang was born in Chongqing，in 1965.He received the M.S.degree from Beijing University of Posts and Telecommunications in 1999.He is now an associate professor and also the instructor of graduate students.His research concerns algorithm of physical layer in LTE systems.

滕旺（1989—），男，安徽芜湖人，2010年于安徽师范大学获电子信息工程专业工学学士学位，现为硕士研究生，主要研究方向为TD-LTE系统OFDM关键技术；

TENGWang was born inWuhu，Anhui Province，in 2010.He received the B.S.degree from Anhui Normal University in 2010. He is now a graduate student.His research concerns LTE system crucial technology of OFDM.

Email：tengwang211＠gmail.com

李小文（1955—），男，重庆人，1988年于重庆大学获信号与系统专业工学硕士学位，现为硕士生导师，主要从事TDLTE综合测试仪表的开发。

LIXiao-wen was born in Chongqing，in 1955.He received the M.S.degree from Chongqing University in 1988.He is now an instructor of graduate students.His research concerns development of TD-LTE integrated test instrument.

An Efficient Im proved Algorithm for Carrier Frequency O ffset Estimation in TD-LTE System

CHEN Fa-tang，TENGWang，LIXiao-wen
（Chongqing Key Lab of Mobile Communication，Chongqing University of Posts and Telecommunication，Chongqing 400065，China）

In view of the importance of frequency offset estimation in the downlink process in TD-LTE system，proposed an improved method is proposed to jointly estimate fraction carrier frequency offset and integral carrier frequency offset in time domain through auto-correct by rotation factor.The

signal is correlated after carrier frequency offset compensation in limited range，and the carrier frequency offset is determined according to the peak value of correlation power.Simulation results demonstrate that the proposed algorithm can improve the reliance and complexity in comparison with the normalmethods and it has significance for reference.

TD-LTE；OFDM；frequency offset estimation；correlation；rotation factor

The National Science＆Technology Major Project（2009ZX03002-009）

TN915

A

10.3969／j.issn.1001-893x.2012.04.012

陈发堂（1965—），男，重庆人，1999年于北京邮电大学获应用数学专业硕士学位，现为副教授、硕士生导师，主要研究方向为LTE的物理层算法；

1001-893X（2012）04-0483-05

2011-11-25；

2012-02-17

国家科技重大专项资助项目（2009ZX03002-009）