运用分频段希尔伯特黄变换进行多分量信号的频散分析✴

蒋礼

（1.中国地质大学（武汉）地球物理与空间信息学院，武汉430074；2.华北水利水电学院数学与信息科学学院，郑州450011）

运用分频段希尔伯特黄变换进行多分量信号的频散分析✴

蒋礼1，2

（1.中国地质大学（武汉）地球物理与空间信息学院，武汉430074；2.华北水利水电学院数学与信息科学学院，郑州450011）

将分频段希尔伯特黄变换应用于多分量信号的频散分析中。首先，利用带通滤波器和经验模态分解相结合，成功实现了经验模态频率分解，并准确提取了经验频率模态函数；然后，使用该方法准确地获取了多分量含噪信号的时频能量谱和时频相位谱；最后，基于同步相差和异步相差算法，精确绘制了原信号的相速度频散分析曲线。数值试验表明，该算法拥有较高的时频分辨能力和良好的抗噪性能，对于复杂且信噪比较低的信号，能获得比传统希尔伯特黄变换更准确的频散分析结果。

希尔伯特黄变换；经验模态频率分解；经验频率模态函数；瞬时频率；频散曲线

1 引言

基于瞬时频率的希尔伯特黄变换（Hilbert-Huang Transform）是一种进行时频分析的有效方法［1］，因为该方法可以准确刻画信号的瞬时频率和瞬时相位，所以它成为进行多分量信号频散分析的有效工具［2-3］。但由于传统希尔伯特黄变换的核心是基于时间序列的经验模态分解，该方法在拥有较高的时间分辨能力的同时往往频率分辨能力较差［4］。虽然对于普通的多分量信号，使用该方法能够取得令人满意的结果，但是对于所含频率分量较多的情况，使用该方法往往不能令人满意。

本文对传统的希尔伯特黄变换进行改进，运用经验模态频率分解理论［5］代替传统的经验模态分解，从而提出分频段希尔伯特黄变换。该方法的频率分辨能力较传统的希尔伯特黄变换有明显提高。将该方法用于进行多分量信号的频散分析，可以得到令人满意的结果。

2 原理简介

传统希尔伯特黄变换的核心为经验模态分解（EMD）和固有模态函数（IMF）。由于经验模态分解进行的是一种时域滤波，所以时间分辨率通常是令人满意的；但由于分解后的固有模态函数个数有限，故频率分辨率往往较低。对于频率成分较为丰富的信号直接进行希尔伯特黄变换通常得不到理想的结果。

2.1 经验模态频率分解

分频段希尔伯特黄变换可以有效解决上述问题。分频段希尔伯特黄变换的核心为经验模态频率分解（EMFD）［5］，它是由北京大学程乾生教授于2005

年提出的一种时频分解理论，初始目的是为了给希尔伯特黄变换提供一组正交基。但在实际应用的过程中，经此方法分解所得的经验频率模态函数（EFMF）不仅正交，而且也具有比固有模态函数更高的频率分辨能力。

假设某一信号s（t）存在K个分量，通过经验模态分解后可得

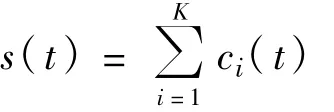
式中，每个ci（t）称为一个固有模态函数。设每个固有模态函数的频谱为Ci（f），由于希尔伯特黄变换的频域分辨率较差，虽然Ci（f）和Ci+1（f）的主频并不相同，但两者在频谱却有不少重叠的部分［6-7］（这也正是传统的固有模态函数不是正交基的原因）。假设两者的主频分别位于fi的两侧，则设定一个理想带通滤波器：Hi（f）=1，fi≤f≤fi-1，其余频段Hi（f）=0，将该滤波器作用于原信号，可得

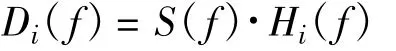
滤波所得信号的时间序列di（t）称为一个经验频率模态函数。上述的整个过程称为一个经验模态频率分解过程。对该多分量信号通过完整的经验模态频率分解可得

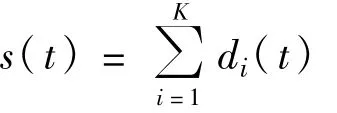
此时不仅由于分解所得的di（t）频谱部分没有重叠，从而构成一组正交基；而且因为分解过程中K个带通滤波器的作用，所以可以准确无误地提取每个频率分量，故该方案具有极高的频率分辨能力。

2.2 时频分析过程

经验模态频率分解的数学原理虽然十分简单，但是按照上述的推导流程来实现整个分解过程将会存在下列难点：

（1）对于一个未知的信号，由于无法预知其频率分量，从而对于滤波器的数目及参数难以确定；

（2）虽然可以在进行经验模态频率分解前先运用经验模态分解来确定滤波器的数目及参数，但这样会浪费分解时间，降低分解效率。

为了高效实现经验模态频率分解过程，可首先在整个频段上设置一系列的频点，将相邻两个频点组成带通滤波器；然后将待分析的信号通过每个带通滤波器可以得到一系列的频段信号；最后对每个分频段信号进行经验模态分解，可以得到每个频段的固有模态函数。这时每个频段的固有模态函数实际上就是经验频率模态函数（每个经验频率模态函数的频谱不会有重叠的部分），而对于分频段信号的经验模态分解过程实际上就是经验模态频率分解过程。

完整的分频段希尔伯特黄变换实现流程如图1所示。与数学推导流程的不同之处在于，数学推导是先进行经验模态分解，而后再制定带通滤波器滤波；而此处对于未知信号是先做带通滤波再做经验模态分解，但两者最终所得结果完全一样（K个固有模态函数即为原信号的K个频率分量，而且频谱部分不会重叠完全正交）。

图1 分频段希尔伯特黄变换算法流程Fig.1 The algorithm flow of sub-band Hilbert-Huang transform

2.3 频散分析过程

对原始多分量信号进行分频段希尔伯特黄变换可以得到时频能量谱和时频相位谱［3］；对上述两谱进行分析，可以获得任意分量信号的瞬时频率、瞬时相位、瞬时能量、持续时间等信息［3］。根据已获知的信息运用同步相差和异步相差理论可以求取任意频率分量的相速度值［3］。完整的频散分析过程如图2所示。

图2 运用分频段希尔伯特黄变换进行频散分析流程Fig.2 The algorithm flow of dispersion analysis by sub-band Hilbert-Huang transform

3 仿真实例

为了验证分频段希尔伯特黄变换的正确性以及较传统希尔伯特黄变换的优越性，此处设定一个较为复杂的多分量信号模型。

3.1 模型建立

假设瑞利波源由10个分量信号叠加而成，初始信号持续时间为0.2 s；各分量信号的群速度和相速度随着频率的增加而减小，且群速度小于相速度；信号能量集中在50 Hz、60 Hz，随着频率的增加和减少，能量依次递减。各分量信号的具体参数详见表1。

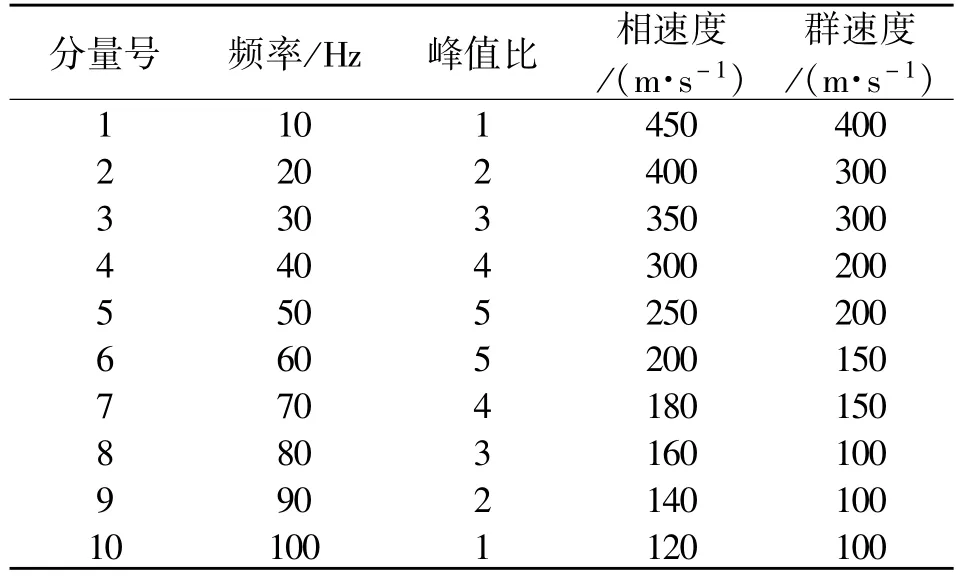
表1 瑞利波源分量参数列表Table 1 Rayleigh wave source component parameter list

两个检波器分别距离震源12 m和18m，检波时间为1.023 s，采样时间间隔为1ms。为了检验该算法的抗噪性能，检波信号除了添加10%的高斯白噪声模拟检波干扰外，再整体添加5%的高斯白噪声作为环境噪声。12m处获取的信号如图3所示，18m处获取的信号如图4所示。

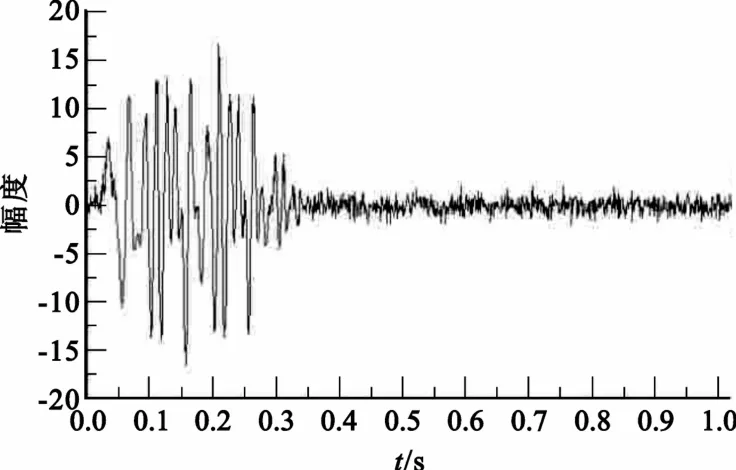
图3 信号1Fig.3 Signal1

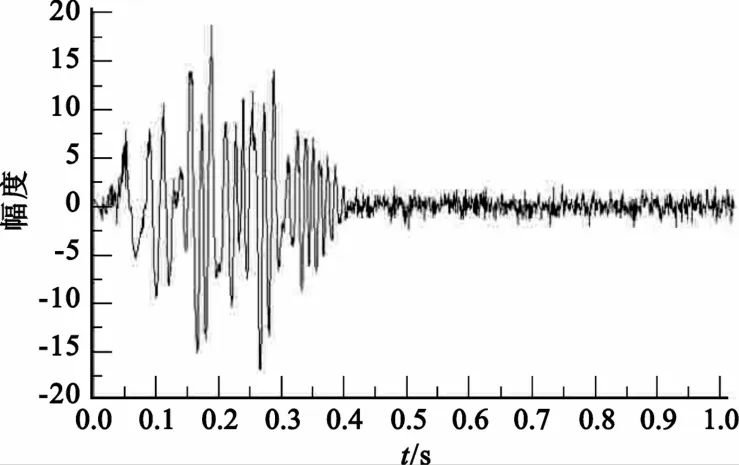
图4 信号2Fig.4 Signal2

3.2 谱分析

3.2.1 希尔伯特黄变换

运用传统希尔伯特黄变换所得谱分析结果如图5所示。图5（a）和（b）分别为12m和18m处信号的时间-频率-能量谱；而图5（c）和（d）则分别为12m和18m处信号的时间-频率-相位谱。从上述各图可以发现，无论是时频能量谱还是时频相位谱都不能准确刻画出10个频率分量的完整信息。虽然由于希尔伯特黄变换良好的时间分辨能力，对比12m处和18m处从高到低的各频率分量能量谱可以清晰地看出频散效应；但是由于不能将10个频率分量的时频信息完整地反映出来，故而无法求取每个分量的准确相速度值。

图5 传统希尔伯特黄变换的谱分析图Fig.5 Spectrum analysis diagram of Hilbert-Huang transform

图6 分频段希尔伯特黄变换的谱分析图Fig.6 Spectrum analysis diagram of the sub-band Hilbert-Huang transform

3.2.2 分频段希尔伯特黄变换

分频段带通滤波器必须预设两个参数：有效频段和滤波器带宽。有效频段反映的是波源信号的物理特性，而带宽则反映了频率分辨能力。理论情况下，无穷大的有效频段和无限小的带宽可以满足任何多分量信号的分解；但在实际应用中，有效频段设定越小，带宽设定越大，则运算效率越高。此处有效频段设为5～105 Hz，以10 Hz为带宽进行窄带滤波。

运用分频段希尔伯特黄变换所得谱分析结果如图6所示。从上述各图可以发现，无论是在时频能量谱还是时频相位谱中，10个频率分量都显示得十分清晰，而且可以看出各分量的瞬时频率非常接近于真实的物理频率，延迟时间、持续时间和能量分布也基本正确。

从图6（a）和（b）中可以看出12m处及18m处的各分量信号均通过0.2 s；18m处的信号各分量均通过0.25 s。为了分析方便，只测量这两个时刻的瞬时频率和瞬时相位，所测量的数据如表2所示（表2中的平均频率为某一分量所有时刻瞬时频率的加权平均［3］）。从表2中可以看出，无论是瞬时频率还是平均频率都非常接近接近于该分量信号的真实物理频率。

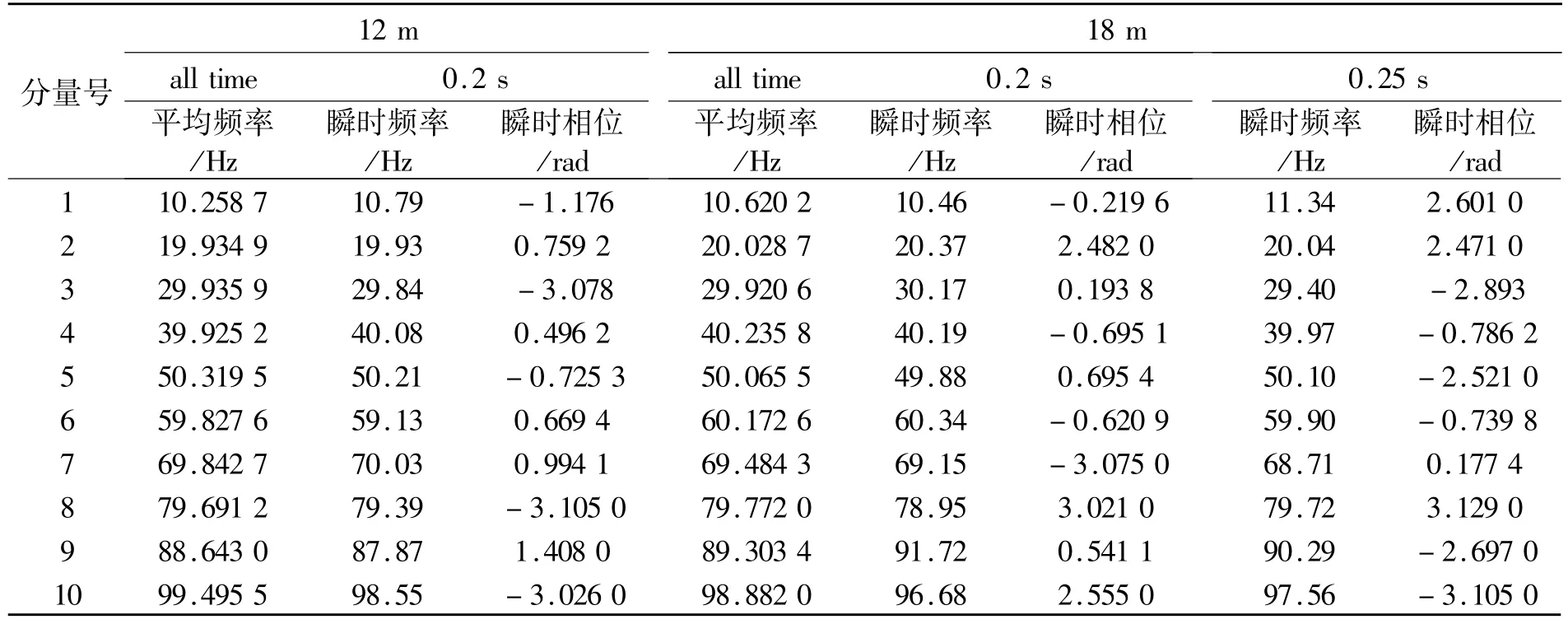
表2 实测时间-频率-相位Table 2 Measured values of time-frequency-phase

3.3 计算结果分析

对表2所测得的数据进行相速度计算，所得结果及误差如表3所示。从计算结果来看，所得相速度较为理想。第三分量至第十分量基本接近于相应模型分量的真实速度；第一分量和第二分量虽然误差较大，但仍在可接受的范围之内。

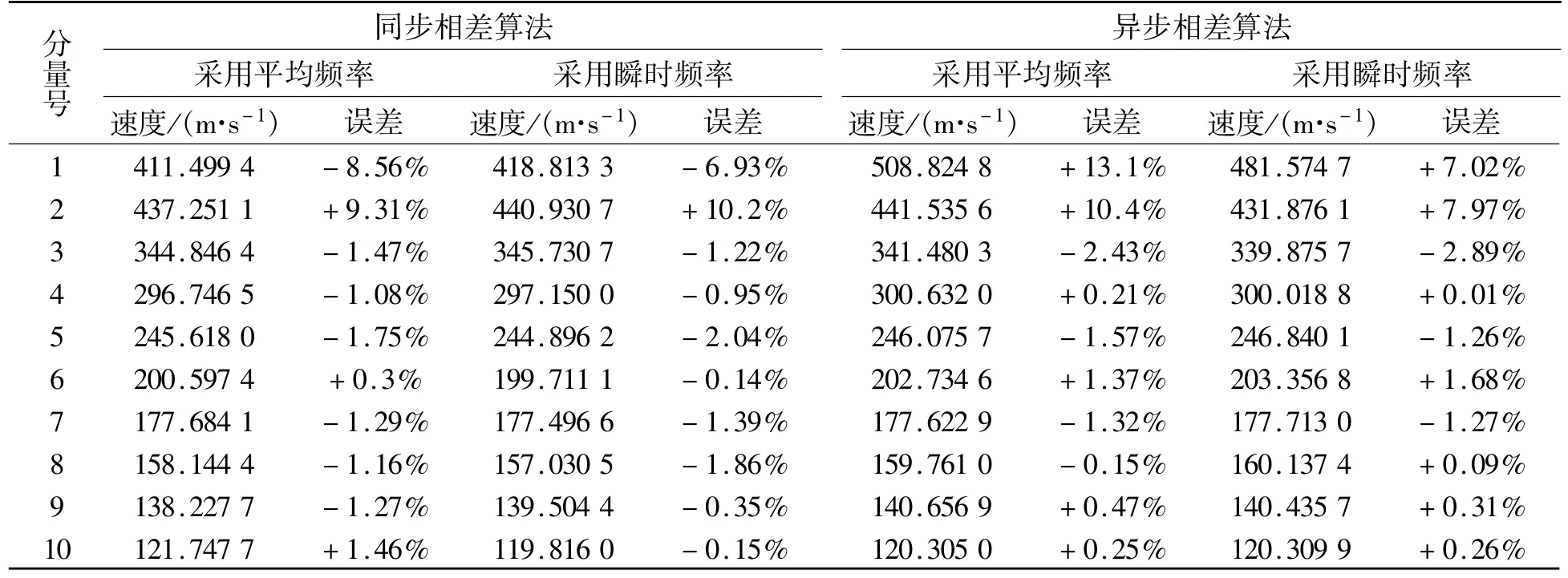
表3 相速度及误差计算结果Table 3 Results of phase velocity and error

上述两个方法出现的误差主要产生于分母部分的相差和频率的比值项Δφ／ω0［3］。理论上Δφ／ω0的误差会随着相位解缠时频率的升高而逐渐减小。

3.4 频散曲线

根据表3的计算结果可以绘制4条频散曲线。若在位于24m的测点处增加一个检波器记录，则可以绘制12条频散曲线。其中8条是道间距为6m的频散曲线，4条为道间距为12m的频散曲线。所有的相速度频散曲线如图7所示。

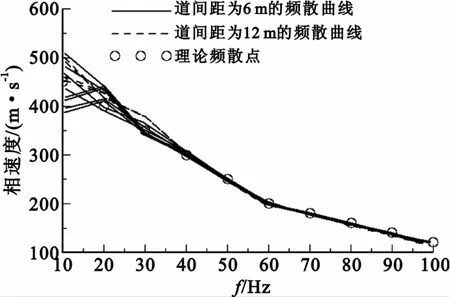
图7 相速度频散曲线Fig.7 Phase velocity dispersion curves

从图7中可以看出，频散曲线正确反应了频散模型的相速度变化规律。随着频率的升高，频散曲线的收敛性越来越好；而且道间距为12m的频散曲线误差要整体小于道间距为6m的频散曲线误差。

4 结论

经验模态频率分解在保留经验模态分解较高的时间分辨能力同时，又提高了频率分辨能力，以其为基础的分频段希尔伯特黄变换具有极为准确的时频-相位定位能力。将该方法用于进行多分量信号的频散分析，不仅计算结果准确，而且具有较强的抗噪能力。

使用该方法时有两个细节需要引起注意。

（1）进行分频段处理时选择合适的频窗，不同窗型及窗口的大小会影响最终的结果。因为进行窄带滤波必然会降低希尔伯特谱的时间分辨率。此时应注意，频窗不应取得太小，窗型不应选择剧烈跳变类型。

（2）如果对源信号各分量的频率成分较为熟悉，则可采用频段交叉的频窗进行窄带滤波，即在不减小窗口大小的情况下使窗口频段交叉（频窗的主频部分不可交叉）。这样可以在相同有效频段的基础上增加带通滤波器的数量，即能够在不降低时间分辨率的同时进一步提高频率分辨率。

运用谱分析方法计算多分量信号的频散特性曲线关键在于两点：准确的时频分析和精确的速度计算。从本文和文献［3］的对比可以看出，S-HHT与传统的HHT相比虽然增加了计算量，但提高了频域分辨能力及抗噪性能。当待分析信号较为复杂或信噪比较差时，使用S-HHT能够获得更准确的时频谱。而同步相差和异步相差算法，在进行相速度计算时精度相似，都是进行频散分析的优秀算法。

［1］Huang N E，Shen Zheng，Long SR.The empiricalmode decomposition and the Hilbertspectrum for nonlinear and nonstationary time series analysis［J］.Proceedings of the Royal Society of London，Series A-Mathematical Physical and Engineering Sciences，1998，454（1971）：903-995.

［2］Chen Chau-Huei，Li Cheng-Pling，Teng Ta-Liang.Surface-Wave Dispersion Measurements Using Hilbert-Huang Transform［J］.Terrestrial Atmospheric and Oceanic Sciences，2002，13（2）：171-184.

［3］蒋礼.运用希尔伯特黄变换进行多分量信号的频散分析［J］.电讯技术，2011，51（7）：60-66. JIANG Li.Frequency Dispersion Analysis of Multi-component Signalusing Hilbert-Huang Transform［J］.Telecommunication Engineering，2011，51（7）：60-66.（in Chinese）

［4］Patrick F，GabrielR，Paulo G.EmpiricalMode Decomposition as a Filter Bank［J］.IEEE Signal Processing Letters，2004，11（2）：112-114.

［5］程乾生，武连文.时间序列的经验模态频率分解EMFD［J］.数学的实践与认识，2005，36（5）：151-153. CHEN Qian-sheng，WU Lian-wen.The EmpiricalMode Frequency Decomposition for Time Series Analysis［J］.Mathematics in Practice and Theory，2005，36（5）：151-153.（in Chinese）

［6］Huang N E，Shen SSP.Hilbert-Huang Transform and Its Application，Interdisciplinary Mathematical Sciences vol 5［M］.London：World Scientific Public Co Information，2005：57-74.

［7］WU Zhaohua，Huang N E.A Study of The Characteristics of White Noise Using The Empirical Mode Decomposition Method［J］.Proceedings of the Royal Society London，Series A-Mathematical Physical and Engineering Sciences，2004，460（2046）：1597-1611.

Analysis of Frequency Dispersion of M ulti-com ponent Signal using Sub-band Hilbert-Huang Transform

JIANG Li1，2
（1.Institute of Geophysics and Geomatics，China University of Geosciences（Wuhan），Wuhan 430074，China；2.College of Mathematics and Information Science，North China University ofWater Resources and Electric Power，Zhengzhou 450011，China）

In this paper，the sub-band Hilbert-Huang transform（S-HHT）is used to analyse the frequency dispersion ofmulti-component signal.Firstly，the band-pass filter and the empiricalmode decomposition are combined to achieve the empiricalmode frequency decomposition（EMFD）successfully，and accurately obtain the empirical frequencymode functions（EFMF）.Secondly，the time frequency energy spectrums and time frequency phase spectrums from multi-componentsignalwith noise are precisely drawn by themethod.Finally，by using the synchronous phase difference and asynchronous phase difference arithmetic the phase velocity dispersion curves are drawn accurately.The numerical results show that the S-HHTarithmetic hashigh time frequency resolution and good resistance to noise.For complex and low Signal-to-Noise Ratio（SNR）signal，the SHHT can get themore accurate results of dispersion analysis than the HHT.

Hilbert-Huang transform；empirical mode frequency decomposition；empirical frequency mode function；instant frequency；dispersion curves

The National Natural Science Foundation of China（No.40974079）

the B.S.degree and the M.S.degree in 2001 and 2004，respectively.He is now a lecturer and currently working toward the Ph.D.degree.His research concerns geoscience-signal analysis and processing

1001-893X（2012）04-0472-06

2011-12-21；

2012-03-09

国家自然科学基金资助项目（40974079）

TN911

A

10.3969／j.issn.1001-893x.2012.04.010

蒋礼（1979—），男，江苏江阴人，2001年获学士学位，2004年获硕士学位，现为博士研究生，讲师，主要从事地学信号的分析及处理。

Email：jlncwu＠126.com

JIANG Li was born in Jiangyin，Jiangsu Province，in 1979. He