转塔式FPSO单点系泊系统受力计算方法

李伟峰，史国友，李 伟，杨家轩

(大连海事大学航海学院，辽宁大连116026)

浮式生产/储油/卸油船(Floating Production Storage＆Off-loading，FPSO)是20世纪80年代中期兴起的一种新型海上石油开采工具，它兼有生产、储油和卸油的功能，一般与水下采油装置和油船共同组成一套完整的生产系统，是目前海洋工程船舶中的高技术产品。FPSO具有机动性和运移性好、抗风浪能力强、生产和储存能力大等特点，因而适应深水采油。另外，FPSO生产系统投资成本低、建设周期短、便于维护和保养等优点。近年来，FPSO市场十分兴旺，有着广阔的应用前景。转塔式FPSO是众多FPSO中的一种，其在船艏部位设STP内转塔简体结构，FPSO首部与转塔结构直接相连而固定与海上，转塔系泊装置则由多根锚链固定于海底。

2009年11月10日，因渤海海域遇大风天气，海洋石油113号FPSO单点系泊距离增大，脱离原设计位置。自此，FPSO的安全问题被提上了一个新的日程，因而对FPSO系泊安全的核算是十分必要的。

1 系统所受外力

影响FPSO系泊系统的主要外力包括风作用力、流作用力和波浪作用力［1－2］。FPSO系统在这3个作用力的合力和转塔系泊系统作用力的共同作用下保持动态平衡状态。

1.1 风作用力

风作用力参照《港口规划与布置》［3］中公式进行计算:

式中:Fw为风作用力，N;ρ为空气密度，取0.123 kg·s2/m4;V为风速，m/s;C为风压系数，按式(2)计算;A，B分别为水面以上船体正面、侧面投影面积，m2，A和B的值满载和压载时分别按式(3)、式(4)进行计算。

上式中:θ为风向与船体中心线夹角，横风时取90°。DW为船舶载重吨位。

1.2 流作用力

流作用力参照交通部行业规范JTJ 215—98《港口工程荷载规范》［4］进行计算:

式中:Ff为水流对船舶产生的作用力，kN;C为水流作用力系数，按式(6)计算;ρ为水的密度，t/m3;V为水流速度，m/s;S为船舶吃水线以下的表面积，m2，按式(7)计算。

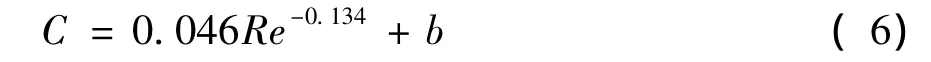
式中:b为系数，取0.015;Re为雷诺数，Re=V·L/v(V是水流速度;L为船舶满载水线长度;v为水的运动黏性系数，其值大小与水温有关)。

式中:D为船舶吃水;B为船宽;Cb为船舶方型系数。

1.3 波浪作用力

波浪作用力计算参照原交通部行业规范JTJ 213—1998《海港水文规范》［5］进行计算。

式中:ρ为海水密度，取1.025 t/m3;H为波高，m;L为波长，m;l为柱体迎浪面的对角线长度，m;d为水深，m;D为船舶吃水，m;θ为波浪作用力与船舶纵轴的夹角，(°)。

1.4 FPSO系统所受合外力计算

假设上述各力的作用点都在船舶中心，根据力的合成原理，系统所受外力示意如图1，合力计算公式如式(9):

图1 力的合成Fig.1 Composition of forces

2 系统锚链受力分析与计算方法

转塔系泊系统通过均匀分布的若干锚链固定在海上，FPSO首部与转塔系泊系统直接相连固定在海上，在外界合作用力和转塔系泊装置作用力的共同作用下保持动态平衡，转塔系泊系统结构如图2。

图2 系泊系统锚链分布Fig.2 Distribution of mooring chains

转塔系泊系统由若干固定于海底的锚链共同作用固定于海上，每根锚链由不同段的锚链相互连接而成，这里假设每根锚链近似为一根悬垂的绳索，并非完全刚性的构件(图3)。

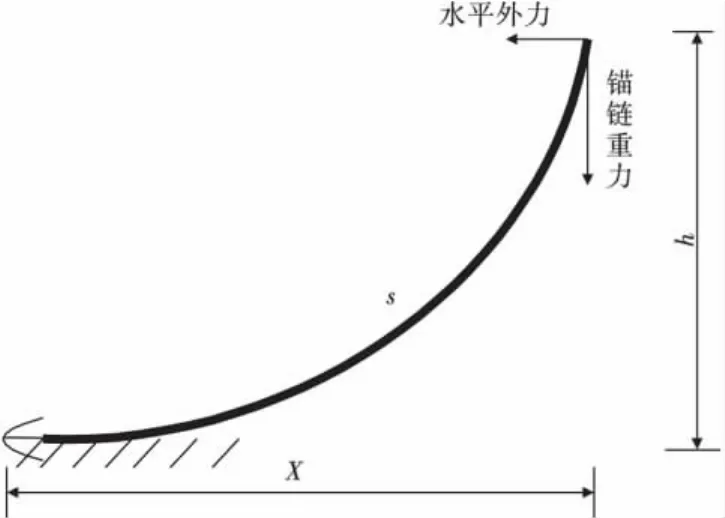
图3 锚链布局图Fig.3 Assignation of the mooring chain

对锚链各部分精确受力的计算是非常困难的，在此通过悬链线方程予以计算［6］:

式中:s为锚链长度，m;X为锚链在水平面内的投影长度，m;h为出链孔至海底的高度，m;a按式(11)计算:

式中:Th为锚链在锚链孔处的水平张力，即单位长度锚链在水中的重量，t/m。

假设转塔式FPSO系泊系统由n根均匀分布的锚链构成，各锚链的初始长度为Si，各锚链固定点坐标为(xi，yi)，转塔位置中心坐标为(xw，yw)。

式中:ω为单位长度锚链在水中的重量，t/m;h为锚链出空口至海底的高度，m;Ti为各锚链张力大小，t;Si为悬链长度，m;Xi为锚链在水平方向上的投影长度，m。

依据方程组(12)，求取在特定的外界环境下FPSO系统作用力中心点所处的地理位置坐标(xw，yw)，及此时各根锚链所受的水平张力Ti，并与锚链所能承受的最大负荷进行比较，进而得出在特定的海况下，系统是否能够安全工作。

3 计算实例

3.1 西江“南海开拓”号FPSO系统概况

3.1.1 “南海开拓”号FPSO主要参数(表1)

表1 “南海开拓”系统主要参数Table 1 The parameters of“South Sea Development”

3.1.2 该海域常年主要水文气象条件

1)风。风速:8 m/s;风向:东北。

2)波浪。浪高1.9 m;周期:6 s;方向:东北。

3)流。流速0.3 m/s;流向正西。

3.1.3 转塔系泊系统及锚链分布

转塔和各锚链固定点中心地理坐标如表2。

表2 锚链固定点坐标Table 2 The coordination of mooring chains

3.1.4 锚链长度

“南海开拓”号FPSO系泊系统各锚链的长度见表3。

表3 锚链长度Table 3 Length of mooring chains/m

3.2 计算结果

锚链在无外力作用时水平投影长度X与各锚链张力T的计算结果如表4。

表4 各锚链水平投影长度Table 4 Length of mooring chains on horizontal

3.2.1 锚链张力与锚链水平长度关系

锚链的水平投影长度与锚链总长度的关系可以用来衡量锚链系统水平方向受力的大小［7］。根据悬链线方程(10)，通过计算机进行建模，进行离散和迭代计算，计算出各锚链在水平方向上的投影长度与该锚链水平方向所受张力的关系，如图4。

转塔式FPSO系泊系统由多根锚链共同作用，其系泊中心点位置也是由各根锚链作用力共同作用的结果，在此也可以通过将各锚链水平长度代替各锚链水平受力大小进行求解［8］。

图4 锚链水平长度与锚链张力关系Fig.4 The relationship between the length on horizon and the force of mooring chain

3.2.2 船舶受力计算

依据所述计算方法，对中国南海西江码头“南海开拓”号FPSO进行受力计算，其计算结果如表5。

表5 FPSO受力详细Table 5 Forces in FPSO system

3.2.3 转塔系泊系统各锚链受力

依据系统模型，分别对满载、半载和空载3种装载状态时转塔式FPSO系泊系统各锚链受力情况进行计算，计算结果如表6。

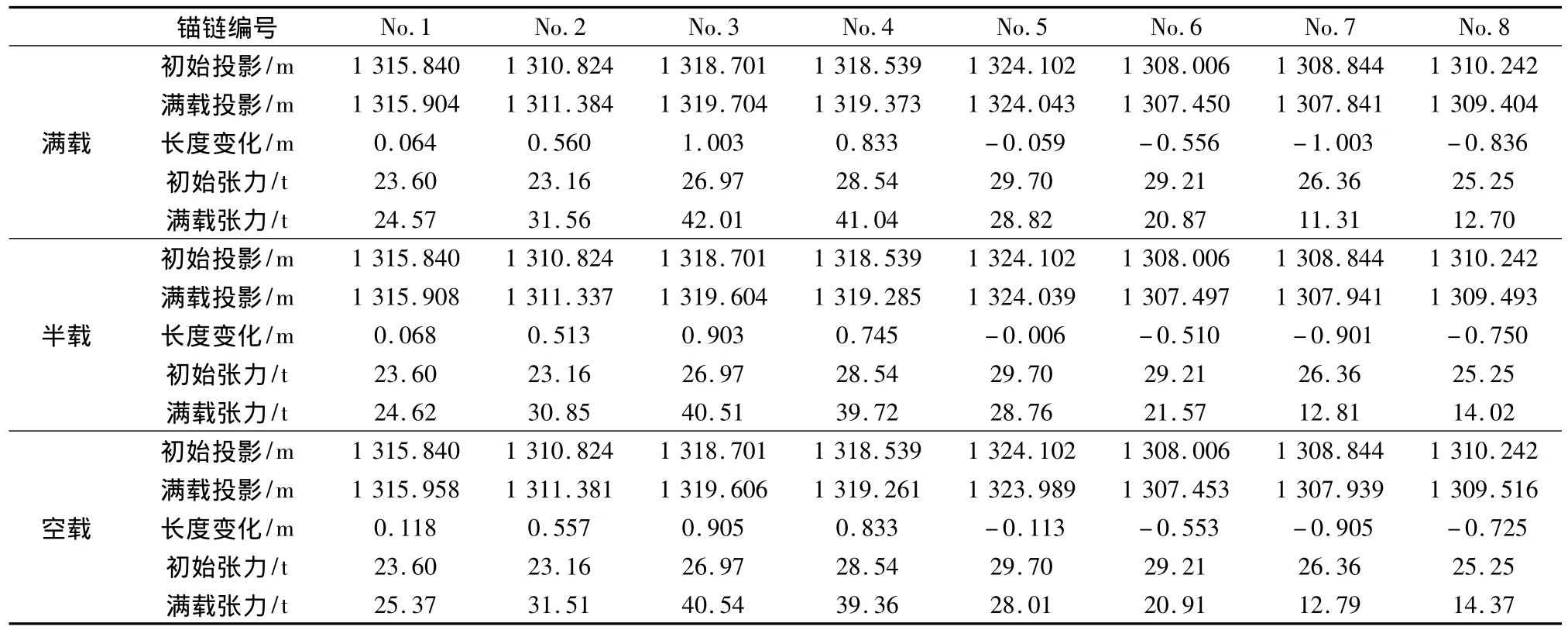
表6 系泊系统各锚链受力Table 6 Forces of mooring chains when fully loaded

3.2.4 系泊系统各锚链实际受力

表7为转塔系泊系统各锚链的实际受力情况。通过表6和表7的对比可知，其计算结果与实际受力情况差别不大，在可接受的范围内。

表7 系泊系统各锚链实际受力Table 7 Actual forces of mooring chains

4 结语

对转塔式FPSO系统所受风、浪、流作用力和系泊系统各锚链的受力情况进行研究和计算，通过静态的方法对系泊系统各锚链受力情况进行核算，建立了相应的数学模型。以“南海开拓”号FPSO为例，分别从满载、半载和空载3种装载状态进行受力计算，计算结果较工程设计时结果略微偏大，但差值在可接受范围以内，且有利于实际安全，表明该计算方法具有一定的使用价值。

［1］麦加宁.深圳蛇口招港12.5万吨级作业浮筒设计简介［J］.水运工程，2000(10):53 －54.Mai Jianing.Shenzhen Shekou China merchants harbor company 125000 DWT operating buoy design［J］.Port＆ Waterway Engineering，2000(10):53 －54.

［2］林正珍，叶燕贻.湄州湾锚地10万吨级系船浮筒设计与施工［J］.水运工程，2000(6):18 －22.Lin Zhengzhen，Ye Yanyi.Design and construction of 100000 DWT mooring buoy in Meizhou bay anchorage［J］.Port＆ Waterway Engineering，2000(6):18－22.

［3］洪承礼.港口规划与布置［M］.北京:人民交通出版社，2007:25－30.

［4］JTJ 215—1998港口工程荷载规范［S］.北京:中华人民共和国交通部，1998.

［5］JTJ 213—1998海港水文规范［S］.北京:中华人民共和国交通部，1998.

［6］刘超.海洋工程锚泊系统计算与分析［D］.武汉:武汉理工大学，2007.

［7］Thomas Telford LTD.Offshore Mooring［M］.London:Institution of Civil Engineers，1982:95 －115.

［8］Gregory P T.Marine Structures Engineering:Specialized Application［M］.3rdEd..New York:Champan ＆ Hall，2002:370 －410.

［9］Chung Jinsug，Michael M B.Hydrodynamic memory effect on stability，bifurcation and chaos of two-point mooring system ［J］.Journal of Ship Research，1997，41(1):26－44.