基于Ordered Probit模型的交通事故受伤人数预测*

宗芳 许洪国 张慧永

(吉林大学交通学院，吉林长春130022)

随着我国社会经济的发展，机动化程度不断提高，道路交通安全形势日趋严峻，交通事故屡有发生.为了采取有效措施来迅速处理交通事故，减少人员伤亡和财产损失，有必要建立交通事故态势分析模型，有效评估交通事故的严重程度和等级，从而制定有针对性的交通事故快速响应方案，尽可能降低交通事故的影响.

事故态势分析是交通安全研究领域的主要研究方向之一.具体包括事故严重程度预测［1-6］、事故持续时间预测［7-13］和事故致因分析［14-15］等方面.其中，交通事故态势预测主要应用Logit模型、有序响应模型等.例如，Sze等［1］以非机动车属性和道路属性为主要影响因素，建立二项Logit模型，预测事故中是否有人员死亡.Kim等［2］将交通事故严重程度按死伤人数分为4个级别，建立多项Logit模型预测事故态势.Lee等［3］将交通事故严重程度按死伤人数分为5个级别，建立了有序响应模型预测态势.国内相关研究较少，马壮林等［4-5］分别应用神经网络模型和二项Logit模型预测公路隧道交通事故的严重程度，其中神经网络模型的因变量为事故严重程度(财产损失事故取0，受伤事故取0.5，死亡事故取1)，Logit模型的因变量为是否有死亡.李世民等［6］应用累计Logistic模型分析交叉口转弯车辆比例、控制方式和土地开发强度对无信号三路交叉口的事故严重性的影响.

纵观以上各模型预测结果的有效性和模型的适用性，交通事故态势预测中如果因变量为二项变量，则较适合采用二项Logit模型;因变量为多项无序变量，适合采用改进的Logit模型(因为Logit模型具有选择枝独立特性)，而不适合采用多项Logit模型;因变量为有序变量(即因变量的取值具有等级关系)，适合采用有序响应模型.另外，在严重程度的预测中最好能够对死亡人数、受伤人数和财产损失3个参量进行单独建模和预测，而且在因变量设置方面也要尽量细致到具体的财产损失额度、受伤人数和死亡人数，从而为事故响应提供更细致的决策依据.同时，在事故严重程度影响因素的选择方面也要尽量全面.

表征交通事故态势的参量主要包括死亡人数、受伤人数和财产损失量.其中死亡人数和受伤人数是决定事故快速响应决策的主要参量，而事故中人员受伤的概率要远大于人员死亡的概率.因此，文中将主要以受伤人数为研究对象，建立交通事故态势的预测模型.因变量将被细化到受伤人数数量，即设置多项的有序因变量.在模型方面则应用有序响应模型中常用的Ordered Probit模型进行参量建模.目的是促进Ordered Probit模型在事故态势预测领域的应用，同时为交通管理部门迅速准确地判断事故态势及做出快速响应提供决策支持.

1 变量和数据

建模样本数据取自长春市2008年的6075起事故.经过初步的经验判断和数据相关性分析，筛选得到事故发生时间等17个变量(见表1).在原始数据中，除受伤人数和能见度为数量变量外，其它变量均为属性变量.为了满足建模要求，参照GA16.1—2003《道路交通事故信息代码》，结合其它相关标准和建模经验，将属性变量编码处理为虚拟变量，将数量变量编码处理为离散变量.各变量的取值及统计所得的均值和标准差见表1.

表1 事故严重程度的影响因素和变量设置Table 1 Factors and variables of accident severity

2 Ordered Probit模型

由于决策变量-受伤人数为多项有序的离散变量，因此采用有序响应模型进行预测.有序响应模型是处理有序离散变量的一类计量经济学模型.根据对残差项条件概率分布做出不同的假定，有序响应模型可分为不同类型，常用的有Ordered Probit模型和Ordered Logit模型.

Ordered Probit模型是进行有序离散变量预测最常采用的模型之一.模型中被解释变量(因变量)的观测值y表示排序结果或分类结果，其取值为有序整数，如 0，1，2，3，….解释变量(自变量)是可能影响被解释变量排序的各种因素，可以是多个解释变量的集合.Ordered Probit模型的一般形式为:

式中:y为因变量;y*称为潜变量或隐性变量;X为解释变量组成的向量;β为X的系数，是待估计参数组成的向量，表示各解释变量对被解释变量影响程度的大小;ε为随机扰动项，代表被模型忽略、但对被解释变量产生影响的其它因素的总和，ε对X的条件分布假设为标准正态分布，即

设 α1、α2、α3为阈值，且 α1＜α2＜α3，并有:

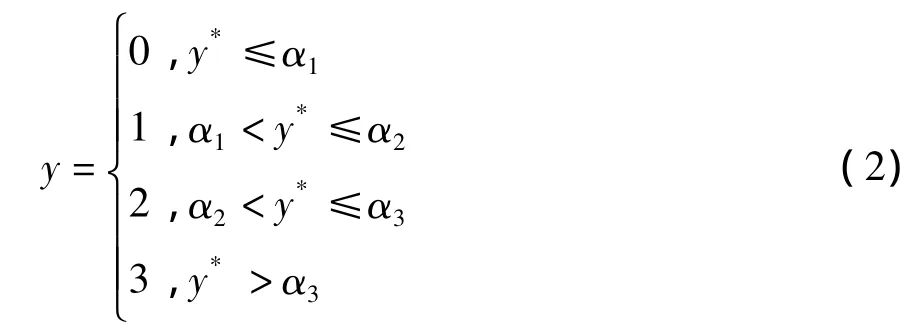
那么，y对X的条件概率的计算方程组为

式中:φ()为标准正态分布的密度函数.

通常，可用极大似然方法对系数β和阈值α1、α2、α3进行估计.

由于Ordered Probit模型自身的特点，变量的系数项β并不能直接说明解释变量对被解释变量的影响大小，甚至系数的符号也只能说明该变量对第一和最后一个选择枝的影响方向，而不能说明对中间选择枝的影响方向.因此，为了进一步了解各变量对被解释变量的影响程度和方向，需要计算各个变量的边际贡献.某个变量的边际贡献指在其它变量取均值时，该变量变动1个单位对某项选择的概率影响.计算式为

3 受伤人数预测模型

3.1 参数标定

根据Ordered Probit理论，建立受伤人数预测模型.模型的选择枝设定为:0表示无受伤人数，1表示受伤人数 =［1，3)，2表示受伤人数 =［3，+∞).在初始建模阶段，假定表1中所有变量均为模型的解释变量，在预测过程中根据检验结果和经验值进行参数的进一步筛选和重新标定.应用Stata软件的Oprobit命令进行模型的参数标定，标定结果如表2所列.

表2 受伤人数预测Ordered Probit模型参数标定结果1)Table 2 Estimation results of Ordered Probit model of injury severity predicion

代入各参数的标定值，得到受伤人数预测Ordered Probit模型:

统计分析各项参数的估计结果可知，经变量筛选后，共有7个自变量对受伤人数产生影响.按影响从大到小的顺序排列，分别为路表是否干燥、是否有中大型车辆、是否在交叉口、天气、是否有摩托车、是否有信号或标志标线、是否在机动车道.

3.2 结果分析

为了进一步明确各自变量对事故受伤人数中各选择枝的影响方向和影响程度大小，由式(4)计算各变量的边际贡献值，结果见表2.根据计算结果，可以分析模型中各参数对3个选择枝分别产生的影响.需要指出的是，由于城市中发生3人以上受伤事故的概率相对于无受伤和受伤为1-3人的概率小，因此在均匀抽样的情况下，受伤人数为［3，+∞)的样本量明显较受伤人数为0或1-3时少，再经过模型标定时误差的放大，导致对受伤人数为［3，+∞)的预测准确性相对较差.此问题导致各参数对选择枝3的影响并不太符合常规想法和经验判断.因此，主要通过各参数的边际贡献计量值考查各参数对选择枝1和2的影响.各变量的分析如下:

(1)变量“天气”对事故受伤人数的影响较大，边际贡献参数的符号与凭经验判断所得的预期影响方向一致.当天气晴好时，发生受伤人数为 0、1-3和3人以上的概率比天气不好时分别低20%、98%和23%.可见，天气状况不好时更容易发生中等受伤人数(1-3人受伤)的事故.天气晴好时更容易发生无人员受伤的事故.

(2)变量“是否有信号或标志标线”对事故受伤人数有影响，但影响程度不大，边际贡献参数的符号基本与预期影响方向一致.结果表明，当事故发生地点设有信号或标志标线等交通安全设施时，发生受伤人数为0和3人以上的概率比没有安全设施时分别高6%和7%.当事故发生地点设有信号或标志标线等交通安全设施时，发生受伤人数为1-3的概率比没有安全设施时低95%.可见，有安全设施的情况下事故的严重程度比没有安全设施时要低，没有安全设施时较易导致事故中有人员受伤.

(3)变量“是否在机动车道”对事故受伤人数有影响，但影响程度不大，边际贡献参数的符号基本与预期影响方向一致.结果表明，当事故发生在机动车道上时，发生受伤人数为0和3人以上的概率比发生在其它车道上时分别高7%和8%;发生受伤人数为1-3的概率比发生在其它车道上时低95%.可见，与非机动车道、人行道等相比，机动车道不易发生人员受伤事故，而非机动车道和人行道由于有非机动车和行人，一旦发生事故容易导致人员伤亡.

(4)变量“是否在交叉口”对事故受伤人数的影响较大，边际贡献参数的符号基本与预期影响方向一致.结果表明，当事故发生地点为交叉口时，发生受伤人数为0、1-3和3人以上的概率比发生在路段等其它位置时分别低21%、98%和23%.可见，由于一般机动车、非机动车和行人到达交叉口时均会减速慢行、注意瞭望，从而使事故的受伤人数降低.反之发生在路段上的事故由于缺乏信号、标志等的提醒，加之交通参与者的疏忽，更容易导致事故严重程度的增加.

(5)变量“是否有摩托车”和“是否有大中型车辆”对事故受伤人数均有一定影响，边际贡献参数的符号与预期影响方向不一致.当事故中有摩托车时，发生受伤人数为0和3人以上的概率比事故中没有摩托车时分别高13%和14%;发生受伤人数为1-3的概率比事故中没有摩托车时低94%.当事故中有大中型车辆时，发生受伤人数为0和3人以上的概率比事故中没有大中型车辆时分别高27%和30%;发生受伤人数为1-3的概率比事故中没有大中型车辆时低92%.在表征事故参与方的车辆类型数据中，除了摩托车和大中型车辆以外，主要为微型、小型和轻型车辆，如小型客车、轻型货车等.结合是否有摩托车和是否有大中型车辆的分析可知，微型、小型和轻型车辆更容易造成1-3的人员死亡事故，与之相比，摩托车和大中型车辆参与的事故的严重程度有所降低.边际贡献参数的符号与预期影响方向不一致的原因主要是进行预期影响方向判定时仅考虑了各项参数单独对结果产生的影响，而没有从所有车辆类型的角度进行总体考虑.

(6)变量“路表是否干燥”对事故受伤人数的影响较大，边际贡献参数的符号基本与预期影响方向一致.结果表明，当路表干燥时，发生受伤人数为0和3人以上的概率比路表潮湿、泥泞等时分别高34%和38%;发生受伤人数为1-3的概率比路表不干燥时低92%.可见，路表湿滑容易导致事故受伤人数的增加，相反当路表干燥时事故的严重程度将有所下降.

4 结语

文中应用Stata软件对所建立的交通事故受伤人数预测Ordered Probit模型进行了参数标定和模型检验，计算了各影响因素的边际贡献，分析了各因素对受伤人数的影响.结果表明，所建模型在进行事故受伤人数预测的同时，也可用于分析各因素对受伤人数的影响方向和影响程度.本研究可为交通管理部门迅速准确地判断事故态势，做出快速响应，提供决策支持.同时，对于Ordered Probit模型在事故态势预测领域的进一步应用以及死亡人数、财产损失等其它表征事故态势参量的预测有一定借鉴作用.

需要说明的是，本研究存在以下缺陷:(1)未对死亡人数、财产损失等其它表征事故态势的参量进行预测，但证明了Ordered Probit模型对于多项的有序离散变量的预测具有较高的预测精度，今后可根据参量的选择枝个数和是否为有序变量，选择Logit模型或Ordered Probit模型进行预测;(2)在数据方面，由于从样本中无法获取事故中人、车速、交通量等相关数据，因此导致建模过程中无法考虑这些重要因素(如车速、肇事者性格特点等)对事故后果的影响.今后应考虑增加相关数据项以完善模型.

［1］Sze N N，Wong S C.Diagnostic analysis of the logistic model for pedestrian injury severity in traffic crashes［J］.Accident Analysis ＆ Prevention，2007，39(6):1267-1278.

［2］Kim J K，Kim S，Ulfarsson G F，et al.Bicyclist injury severities in bicycle motor vehicle accidents［J］.Accident Analysis ＆ Prevention，2007，39(2):238-251.

［3］Lee C，Abdel-Aty M.Comprehensive analysis of vehicle pedestrian crashes at intersections in Florida［J］.Accident Analysis and Prevention，2005，37(4):775-786.

［4］马壮林，邵春福，李霞.高速公路隧道交通事故严重程度的影响因素分析［J］.北京交通大学学报，2009，33(6):52-55.Ma Zhuang-lin，Shao Chun-fu，Li Xia.Analysis of influence factors on severity for traffic accidents of expressway tunne［J］.Journal of Beijing Jiaotong University，2009，33(6):52-55.

［5］马壮林，邵春福，李霞.基于Logistic模型的公路隧道交通事故严重程度的影响因素［J］.吉林大学学报:工学版，2010，40(2):423-426.Ma Zhuang-lin，Shao Chun-fu，Li Xia.Analysis of factors affecting accident severity in highway tunnels based on Logistic mode［J］.Journal of Jilin University:Engineering and Technology Edition，2010，40(2):423-426.

［6］李世民，孙明玲，关宏志.基于累积 Logistic模型的交通事故严重程度预测模型［J］.交通标准化，2009，190/192(2/3):168-171.Li Shi-min，Sun Ming-ling，Guan Hong-zhi.Prediction model cumulative Logistic for severity of road traffic accident［J］.Transport Standardization，2009，190/192(2/319):168-171.

［7］王发智.基于贝叶斯网络的交通突发事件态势评估技术［D］.大连:大连理工大学计算机学院，2006.

［8］Golob T F，Wilfred W R，John D L.An analysis of the severity and accident duration of truck-involved freeway accidents［J］.Accident Analysis ＆ Prevention，1987，19(5):375-395.

［9］Jones B L，Janssen F M.Analysis of the frequency and duration of freeway accidents in Seattle［J］.Accident A-nalysis ＆ Prevention，1991，23(4):239-255.

［10］Wang M.Modeling freeway accident clearance time［D］.Northwestern:Civil＆Engineering Dept，Northwestern University，1991.

［11］姬杨蓓蓓.交通事件持续时间预测方法研究［D］.上海:同济大学交通运输工程学院，2008.

［12］Xu Hong-guo，Zhang Hui-yong，Zong Fang.Trafic incident duration analysis using hazard duration model［C］∥TMEE.Changchun:IEEE，2011.

［13］陈玲娟，刘海旭，蒲云.事故影响下走行时间及择路概率的动态分析［J］.华南理工大学学报:自然科学版，2012，40(2):63-69.Chen Ling-juan，Liu Hai-xu，Pu Yun.Dynamic analyses of travel time and route choice probability of users in accidents［J］.Journal of South China University of Technology:Natural Science Edition，2012，40(2):63-69.

［14］Xu Hong-guo，Zhang Hui-yong，Zong Fang.Bayesian network-based road traffic accident causality analysis［C］∥ICIE.Chengdu:IEEE，2010.

［15］Chong M，Abraham A.Traffic accident analysis using machine learning paradigms［J］.Computational Intelligence in Data Mining，2005，29(5):89-98.