基于三维离散元法的沥青混合料断裂过程模拟*

陈俊 黄晓明

(1.河海大学 土木与交通学院，江苏南京210098;2.东南大学 交通学院，江苏南京210096)

沥青混凝土的断裂性能一直以来都是道路工作者关注的热点.在过去的几十年间，人们采用了多种研究手段对沥青混凝土的断裂性能进行测试和分析，其中间接拉伸试验和小梁弯曲断裂试验等室内宏观测试是最为普遍的研究方法.此类方法能容易获得沥青混凝土的断裂强度和极限应变，并能以此为基础，进行基于断裂性能的沥青混凝土组成材料的优选.但是，由于沥青混凝土的力学性能在很大程度上取决于其内部集料和空隙的体积含量、排列分布特征，而宏观尺度的室内试验却不能充分考虑混凝土的细观结构，因此此种方法对于深入理解沥青混合料材料断裂本质特征、准确把握材料的断裂机理不能起到积极作用.

近年来，伴随着图像处理技术和计算机科学的快速发展，沥青混凝土内部空间细观结构的获取引起人们越来越多的关注.在获得沥青混凝土结构的基础上，人们采用诸如有限元、离散元和边界元之类的计算机分析软件，试图建立细观结构与宏观性能的关系.如Sadd等［1-2］曾采用有限元方法从细部结构入手预测沥青混合料的宏观模量.在此基础上，Dai等［3］还运用有限元研究了沥青混合料模量的各向异性问题.然而，随着有限元方法在材料领域的广泛应用，其难以模拟粗集料和沥青砂浆的界面形状、不适合处理刚柔接触问题和模拟材料大变形的缺陷逐渐被人们所认识.

作为一种新发展起来的数值模拟方法，离散元法凭借其能够处理应力不连续、大变形问题等方面的优势，在道路材料领域的应用越来越广泛［4-7］.总体而言，离散元法在沥青混合料性能模拟方面的研究大体可分为两个阶段.第一阶段为2008年前，这期间Rothenburg等［8-12］对二维离散元方法应用于沥青混合料性能分析的可行性进行了研究，其主要研究思路是:采用对沥青混合料试件的截面进行数码照相;运用图像处理技术，把数码图像转化为数字试件，并导入到离散元软件内，生成沥青混合料的二维数字试件;最后，进行沥青混合料的力学模拟试验.这期间研究工作的特点是:①以二维离散元分析为主，没有开展三维分析;②沥青材料假定为弹性，忽略其粘弹性特征.第二阶段是2008年后，You等［13］开展了沥青混合料三维结构重构的研究，研究方法是对沥青混合料试件每隔一定高度h(≥8mm)进行切割，并对切割后的截面数码照相，获得n个二维数字试件，然后在离散元软件内把n个二维试件重构为三维试件.重构过程中，在高度为h的空间内采用的是同一个二维试件.这样做虽然能建立三维试件，但是试件内部集料的形状、空间布局等等都与实际试件差距较大，导致了集料与集料的嵌锁作用不能得以体现.另外，关于沥青材料的粘弹性特征，Liu等［14］建立了Burgers模型中各元件微观参数的确定方法，但并没有应用于三维结构的分析.由此可见，离散元方法应用于沥青混合料性能模拟分析仍有诸多问题尚待解决，表现为:①如何在沥青混合料三维结构性能模拟中考虑沥青材料的粘弹性特征;②二维模型的建立方法受照相技术、图像处理过程的影响较大，而且试件的成型只是为了获得其截面的数码相片，造成了较多人力和物力的浪费;且混合料二维模型并不能考虑集料的嵌锁作用和空隙的分布特征;③沥青混合料真实三维空间结构的获取需要采用具有较大功率的CT扫描设备，而目前这些设备在我国道路材料研究领域还相当缺乏，如何运用离散元技术直接建立能够考虑集料颗粒不规则形状、集料级配特征和空隙特征的混合料试件仍需研究.

为此，文中采用三维离散元颗粒流软件(PFC3D)，通过自行编写的颗粒生成程序，结合颗粒随机投放算法，建立了可以考虑集料颗粒空间不规则形状、集料级配特征和空隙大小的混合料小梁试件的三维模型;在－10和15℃温度条件下进行了考虑粘弹性特征的小梁试件中点弯曲试验模拟，并与实际试验结果比较，验证了离散元模型的正确性.

1 沥青混合料的三维离散元模型

1.1 集料颗粒的空间不规则形状

大量研究表明，集料尤其是粗集料颗粒的不规则形状对沥青混合料宏观力学行为具有显著的影响［15］，在建立沥青混合料三维离散元模型时，应当充分考虑集料的不规则形状.为此，参照Lu等［16］关于不规则颗粒生成的研究成果，直接在PFC3D内以多个球形单元按照一定的算法相互重叠形成“clump”模拟颗粒.图1为不同粒径粗集料的典型颗粒形状.

图1 典型颗粒的不规则形状Fig.1 Representative irregular shape of aggregate particles

对于上述生成的任一颗粒，其体积按照下式计算

式中:n、m分别为一个集料颗粒内所包含的球形单元数和重叠个数;Vi为集料颗粒内第i个球形单元的体积;Voverlapj为第j个重叠部分的体积，

式中:R1，j、R2，j分别为形成第 j个重叠的两个球形单元的半径;h1，j、h2，j分别为两个球形单元重叠部分球冠的高度.将式(1)和式(2)编制子程序嵌入到PFC3D内，可以方便地计算出各个集料颗粒的体积，在集料密度设定后，即可获得每个颗粒的质量，这就为按照集料质量级配建立混合料离散元模型奠定了基础.需要说明的是，在集料颗粒生成的过程中，颗粒的棱角丰富程度、集料的形状(扁平率等)都可以通过颗粒生成算法内的形状参数加以改变.

1.2 集料混合料的三维离散元模型

考虑到沥青混合料中2.36mm以下的集料与沥青胶结料组成的沥青砂浆材料的力学特征比较稳定，兼顾到离散元计算效率的要求，文中的沥青混合料离散元模型认为是由2.36mm以上的粗集料颗粒和沥青砂浆、空隙所组成.把上述集料颗粒按照一定的级配，投放于长、宽和高分别为300 mm、50 mm和50mm的沥青混合料小梁试件的空间内.投放算法步骤如下:①按照集料粒径由大至小逐级投放;②每投放完毕一个集料颗粒，判断该颗粒与已投放颗粒是否重叠、该颗粒是否在设定的投放空间区域内;若满足要求，则可以进行下一集料颗粒的投放，否则重复本步骤;③判断该颗粒投放后，该档集料质量是否达到设定的质量，若没达到，则开始该档下一集料的投放，若达到，则开始投放粒径较小的下一档集料.

采用上述投放算法，按表1中的级配进行粗集料颗粒的投放，形成如图2所示的具有级配特征的粗集料混合物，其中13.2～16mm为120g(8个集料颗粒)、9.5 ～13.2mm 为360g(145 个颗粒)、4.75 ～9.5mm 为 480 g(810 个颗粒)、2.36 ～4.75 mm 为240g(4505个颗粒).值得注意的是，粗集料投放过程中，各档集料的质量和粗集料总体的质量可以按照研究任务的不同任意设定，也就是说上述算法充分考虑了集料的级配特征和粗集料的体积含量.在集料混合物所在的长方体空间内，按照单元矩形排列的方式(每个球形单元与周围的6个相邻单元相接触)布满半径为1mm的球形单元，共93750个.判断新布满的单元与原有集料颗粒的位置关系，若重叠，则将新单元视为集料单元，若不重叠，则视为沥青砂浆单元.删除原有集料颗粒后，就建立了包含粗集料和沥青砂浆的沥青混合料梁式试件，如图3所示.

表1 集料级配Table 1 Gradation of the aggregate blend

图2 具有级配特征的集料颗粒混合物Fig.2 Aggregate blend with the given gradati

图3 沥青混合料梁式试件的离散元模型Fig.3 Discrete element model of beam-type specimem of asphalt mixture

为了考虑沥青混合料内部的空隙，在图3所示三维模型的沥青砂浆内部，按照空隙的大小随机删除一定数量的球形单元，以模拟空隙在混合料内部的存在.这样处理的理由是，根据Masad等［17］的研究，沥青混合料截面上的单个空隙面积在0.56～3mm2之间，与文中球形单元的面积相当.图4为在如图3所示的混合料三维结构内随机删除了2812个砂浆单元以模拟3%的空隙率的模型.

图4 沥青混合料内部的空隙分布Fig.4 Illustration of air void in asphalt concrete

2 离散元微观力学参数

2.1 宏观与微观力学参数

在上述离散元模型内，涉及到沥青砂浆内部单元、集料内部单元以及集料单元与砂浆单元的接触与粘结问题，文中以PFC3D内的线弹性刚度模型模拟集料内部单元的接触状态，以Burgers模型表征沥青砂浆间单元的粘弹性接触.由于PFC3D内材料性能的输入是微观参数，因此对于规则排列的单元可以由宏观力学参数推导得到微观参数.

对于线弹性模型，采用下式确定微观结构内单元线弹性接触刚度来作为PFC3D内参数的输入:

式中:kn为单元的法向接触刚度;R为单元的半径;E为材料宏观模量.

关于Burgers模型内参数的确定，Liu等［14］建立了模型内各元件微观参数与宏观参数的关系:

式中:L为沥青混合料离散元模型内相邻单元的半径之和;E1、η1分别为Maxwell内弹簧的劲度和粘壶的黏度;E2、η2分别为Kelvin内弹簧劲度和粘壶的黏度;Kmn、Cmn分别为Maxwell内弹簧微观劲度和粘壶的微观黏度;Kkn、Ckn分别为Kelvin内弹簧微观劲度和粘壶的微观黏度.E1、η1、E2和 η2可以根据下式计算得到:

式中:E*为复数弹性模量;ω为试验频率;θ为滞后角.

2.2 宏观力学参数的测试

上述微观参数的计算过程中，需要确定材料(尤其是沥青砂浆)的Burgers模型的各元件参数，以及沥青砂浆材料的抗拉强度.为此，在室内首先成型沥青砂浆的圆柱体试件，沥青砂浆的级配按照表1所示的2.36mm粒径以下的细集料级配确定，假定沥青膜厚度为8 μm，计算得到的沥青用量为14%.需要说明的是，沥青砂浆试件成型时，由于其具有较大的沥青用量，因而往往不需要外力击实就能自密成型.在SPT材料试验机上，进行－10和15℃下频率为10Hz的动态压缩试验，并按照式(8)－(11)计算得到4个元件的参数，结果见表2.

表2 －10和15℃时的Burgers模型参数Table 2 Parameters in Burger’s model at －10 and 15℃

此外，按照上述级配和沥青用量成型沥青砂浆的马歇尔试件，在UTM试验机上进行材料的劈裂试验，测试得到的－10和15℃抗拉强度，分别为5.0和 2.1 MPa.对于集料的模量按照 You［10］的研究成果，取55.5GPa.考虑到沥青混合料弯曲断裂时集料颗粒断裂的情形很少，因此集料内部单元之间的抗拉强度可以取大值，确保其不破坏即可.

3 沥青混合料弯曲断裂模拟与验证

对图3所示的沥青混合料离散元模型，约束两端底部的竖向自由度，对小梁的中点位置施加速率为50 mm/min的竖向荷载，进行三维结构的弯曲断裂模拟.图5给出了三维结构和其中某个二维截面的加载示意图，以及二维截面断裂后的形状.

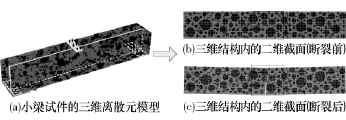
图5 小梁弯曲断裂的离散元模拟结果Fig.5 DEM simulation results of beams bending fracture

图6给出了梁跨中底部不同拉应变时，小梁中部60mm区域内单元之间粘结失效情况，以清晰反映试件的断裂过程.从图中可以看出，随着梁底拉应变的增大，梁中部局部位置单元之间出现了粘结失效，由此可以清晰地看出梁内裂纹的扩展情况.不仅如此，对上述的粘结失效，按照失效位置的不同，分为沥青砂浆内单元之间的粘结失效和砂浆与集料界面位置的粘结失效两类，采用PFC分别采集了图5(b)小梁内两类粘结失效的数量，如图7所示.

图6 不同拉应变时小梁内部的粘结失效情况Fig.6 Failed bonds in the beam at different levels of tensile strain

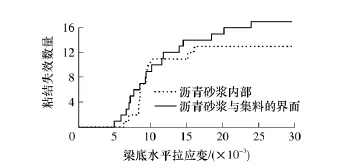
图7 不同部位的粘结失效数量Fig.7 Number of failed bonds at different locations

从图7中清晰地看出，粘结失效(裂纹)在沥青砂浆和砂浆与集料界面上的数量随着梁底拉应变的变化情况.从上述分析和采集的数据可以看出，三维离散元模拟可以很好地模拟出梁式试件的断裂过程，尤其是裂纹在试件内的出现和扩展的数量、发生部位情形，这为从细观结构角度分析混合料断裂特征提供了良好的手段.

在上述小梁弯曲断裂的模拟过程中，采用PFC每隔10个计算时步采集梁底60mm范围内的拉应变和竖向压力，并按式(12)计算梁底拉应力σt:

式中:L'为小梁试件的跨径，mm;P为对小梁施加的最大压力，N;w为小梁的平均宽度，mm;h为小梁平均高度，mm.同时，为了比较分析模拟结果与室内实际试验结果的差距，采用的室内成型沥青混合料小梁试件的级配和沥青用量与断裂模拟相同，试件的空隙率也按照三维离散元模型的3%加以设计.采用与小梁断裂弯曲模拟相同的加载条件分别在－10和15℃温度条件下进行室内断裂试验，并采集了小梁弯曲断裂过程中梁底拉应力和拉应变的关系曲线.图8给出了不同温度下小梁弯曲过程中跨中梁底拉应力与拉应变的实测结果与离散元模拟结果.

图8 离散元模拟结果与实测结果的比较Fig.8 Comparisons between DEM simulation results and experimental ones

由图8可以看出，在相同混合料级配、沥青用量和空隙率时，三维离散元的模拟结果曲线与实测结果整体相差无几，只是在曲线的局部位置处应力和应变值略有差异.其原因可能是:尽管室内成型的试件与文中建立的三维离散元模型具有相同的沥青用量、级配和空隙大小，但是它们内部的细观结构尤其是粗集料和空隙的分布却不尽相同，由此引起了断裂曲线存在一定的差异.通过上述分析可见，文中所建立的三维离散元模型可以较好地模拟沥青混合料弯曲断裂尤其是裂纹出现和扩展的情形，其模拟结果基本上与实测结果保持一致，说明文中所建立的三维离散元模型能够反映混合料的断裂特征，三维离散元模拟可以作为研究沥青混合料弯曲断裂的辅助手段.

4 结语

文中运用离散元颗粒流程序PFC3D内的“Fish”语言，编写了集料颗粒空间不规则形状生成的程序，并结合颗粒随机投放算法和计算机编程技术，建立了可以考虑粗集料形状、级配特征和空隙大小的沥青混合料小梁试件的三维离散元模型.三维离散元模型的建立方法为从微细观结构角度研究沥青混合料的宏观性能奠定了基础.

文中还根据材料宏观力学性能与微观力学参数的关系，结合沥青砂浆的室内性能试验，获得了沥青砂浆粘弹性参数和各类微观参数作为离散元力学试验模拟的输入;并运用三维离散元方法，实现了小梁试件中点弯曲断裂试验的模拟，通过观察模拟过程的现象，以及与室内实际试验结果的比较分析，验证了离散元弯曲断裂模拟的正确性.小梁弯曲断裂模拟为研究沥青混合料断裂性能提供了辅助手段.

［1］Sadd M H，Dai Q L.A comparison of micro-mechanical modeling of asphalt materials using finite elements and doublet mechanics［J］.Mechanics of Materials，2005，37(6):641-662.

［2］Dai Q L，Sadd M H，You Z P.A micromechanical finite element model for linear and damage-coupled viscoelastic behaviour of asphalt mixture［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2006，30(11):1135-1158.

［3］Dai Q L，You Z P.Prediction of creep stiffness of asphalt mixture with micromechanical finite-element and discreteelement models［J］.Journal of Engineering Mechanics，2007，133(2):163-169.

［4］Cundall P A，Strack O D L.A discrete numerical model for granular assemblies［J］.Géotechnique，1979，29(1):47-65.

［5］陈俊，黄晓明.基于离散元法的沥青混合料虚拟疲劳试验方法［J］.吉林大学学报:工学版，2010，40(2):435-440.Chen Jun，Huang Xiao-ming.Virtual fatigue test of asphalt mixture based on discrete element method［J］.Journal of Jilin University:Engineering and Technology Edition，2010，40(2):435-440.

［6］Chen Jun，Huang Xiao-ming.Virtual fracture test of asphalt mixture based on discrete element method［J］.Journal of Southeast University:English Edition，2009，25(4):518-522.

［7］陈俊，黄晓明.集料分布特征对混合料疲劳性能的影响分析［J］.建筑材料学报，2009，12(4):442-447.Chen Jun，Huang Xiao-ming.Research on influence of distribution characteristics of aggregate on fatigue performance of asphalt mixture ［J］.Journal of Building Materials，2009，12(4):442-447.

［8］Rothenburg L，Bathurst R J.Numerical simulation of idealized granular assemblies with plane elliptical particles［J］.Computers and Geotechnics，1991，11:315-329.

［9］Buttlar W G，You Z P.Discrete element modeling of asphalt concrete:a micro-fabric approach［J］.Transportation Research Record:Journal of the Transportation Research Board，2001，1757:111-118.

［10］You Z P.Development of a micromechanical modeling approach to predict asphalt mixture stiffness using the discrete element method［D］.Urbana-Champaign:University of Illinois at Urbana-Champaign，2003.

［11］Kim H，Buttlar W G.Discrete fracture modeling of asphalt concrete［J］.International Journal of Solids and Structures，2009，46(13):2593-2604.

［12］Kim H，Wagoner M P.Micromechanical fracture modeling of asphalt concrete using a single-edge notched beam test［J］.Materials and Structures，2009，42(5):677-689.

［13］You Z P，Adhikari S，Dai Q L.Three-dimensional discrete element models for asphalt mixtures［J］.Journal of Engineering Mechanics，2008，134(12):1053-1062.

［14］Liu Y，Dai Q L，You Z P.Viscoelastic model for discrete element simulation of asphalt mixtures［J］.Journal of Engineering Mechanics，2009，135(4):324-333.

［15］Pan T，Tutumluer E，Carpenter S H.Effect of coarse aggregate morphology on permanent deformation behavior of hot mix asphalt［J］.ASCE Journal of Transportation Engineering，2006，132(7):580-589.

［16］Lu M，Mcdowell G R.The importance of modelling ballast particle shape in the discrete element method ［J］.Granular Matter，2007，9:69-80.

［17］Masad E，Jandhyala V K，Dasgupta N，et al.Characterization of air void distribution in asphalt mixes using X-ray computed tomography［J］.Journal of Materials in Civil Engineering，2002，14(2):122-129.