预应力混凝土斜拉桥收缩徐变效应的概率分析*

苏成 陈兆栓 徐郁峰 庞键

(1.华南理工大学土木与交通学院，广东广州510640;2.华南理工大学亚热带建筑科学国家重点实验室，广东广州510640)

收缩徐变是混凝土材料的固有特性，对于预应力混凝土斜拉桥，由它引起的结构效应，即收缩徐变效应可以在结构总效应中占到相当大的比例，故收缩徐变对预应力混凝土斜拉桥的影响是不可忽略的.同时，预应力混凝土斜拉桥施工及运营过程中存在众多不确定的影响因素，致使结构的收缩徐变效应具有随机性.收缩徐变计算参数的随机性是导致混凝土收缩徐变效应变异的一个重要因素，研究这些参数变异所导致的收缩徐变效应的随机特性，于评估收缩徐变对预应力混凝土斜拉桥的影响有重要意义.

收缩徐变效应与应力历史及混凝土龄期密切相关，因此预应力混凝土斜拉桥收缩徐变效应分析必须考虑结构的施工过程.施工过程模拟采用的是增量有限元法［1-2］，这使得常用的随机分析方法，如摄动随机有限元法［3-4］及蒙特卡罗法，很难适用.采用摄动随机有限元法进行随机分析时，需要修改确定性分析有限元程序的核心算法，不便于工程应用;而且，以全量形式表达的摄动随机有限元法无法适用于表达为增量形式的施工过程模拟.蒙特卡罗法须进行大量的样本试验，对于预应力混凝土斜拉桥收缩徐变效应分析，基于增量有限元法的样本试验意味着庞大的运算量，这对于现有的计算条件是不现实的.

文中拟采用响应面－蒙特卡罗法［5-6］进行预应力混凝土斜拉桥收缩徐变效应随机分析.该法是响应面拟合技术与蒙特卡罗试验的结合，能够避免由于直接使用蒙特卡罗法而面临的运算量过大的问题，又保留了蒙特卡罗法概念直观的优点，适用于施工过程复杂的预应力混凝土斜拉桥收缩徐变效应概率分析.利用该方法，文中还通过单个参数引致的收缩徐变效应的标准差，考察了不同的收缩徐变参数对结构响应的影响程度.在随机分析的基础上，进一步引入区间估计的概念，获得不同置信度下的收缩徐变效应置信区间.在收缩徐变模型方面，文中采用的是JTG D62—2004《公路钢筋混凝土及预应力钢筋混凝土桥涵设计规范》［7］推荐的计算模型.最后，文中利用上述方法对广州绕城公路甘竹溪大桥的收缩徐变效应进行概率分析，验证了所提方法的有效性.

1 混凝土收缩徐变计算模型

《公路钢筋混凝土及预应力钢筋混凝土桥涵设计规范》给出了推荐使用的混凝土收缩徐变计算模型，该模型给出了收缩应变及徐变系数的具体计算方法.其中，收缩应变的计算方法如下:

式中:t为混凝土龄期，d;ts为混凝土开始收缩时的龄期，d;εcs(t，ts)表示开始收缩龄期 ts、混凝土龄期t时的收缩应变;εcs0为名义收缩系数;βs(t，ts)为收缩应变随时间发展的系数.εcs0、βs(t，ts)可分别按式(2)、(3)计算:

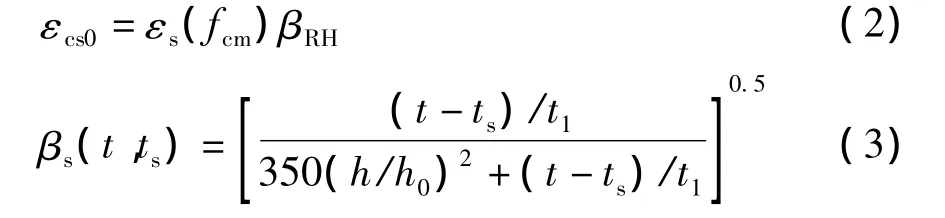
其中:

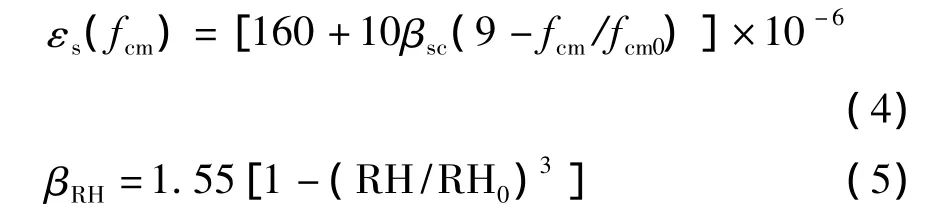
fcm为28d龄期的混凝土立方体平均抗压强度，MPa;βsc为依水泥种类而定的系数;βRH为与年平均相对湿度RH(%)相关的系数;h为混凝土构件的理论厚度，mm;常系数 fcm0=10 MPa，RH0=100%，h0=100mm，t1=1d.

徐变系数表达式为

式中:t0为加载时的混凝土龄期，d;φ(t，t0)表示加载龄期t0、混凝土龄期t时的徐变系数;φ0为名义徐变系数;βc(t，t0)为加载后徐变随时间发展的系数.φ0、βc(t，t0)可分别按式(7)、(8)计算:

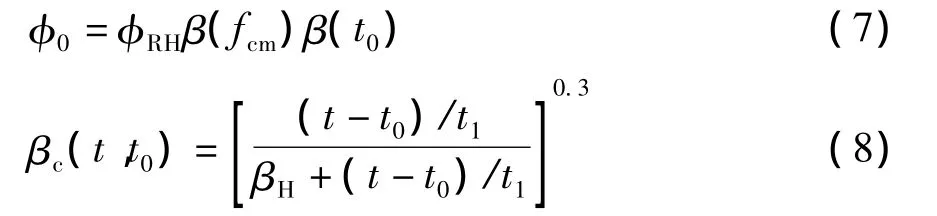
其中:

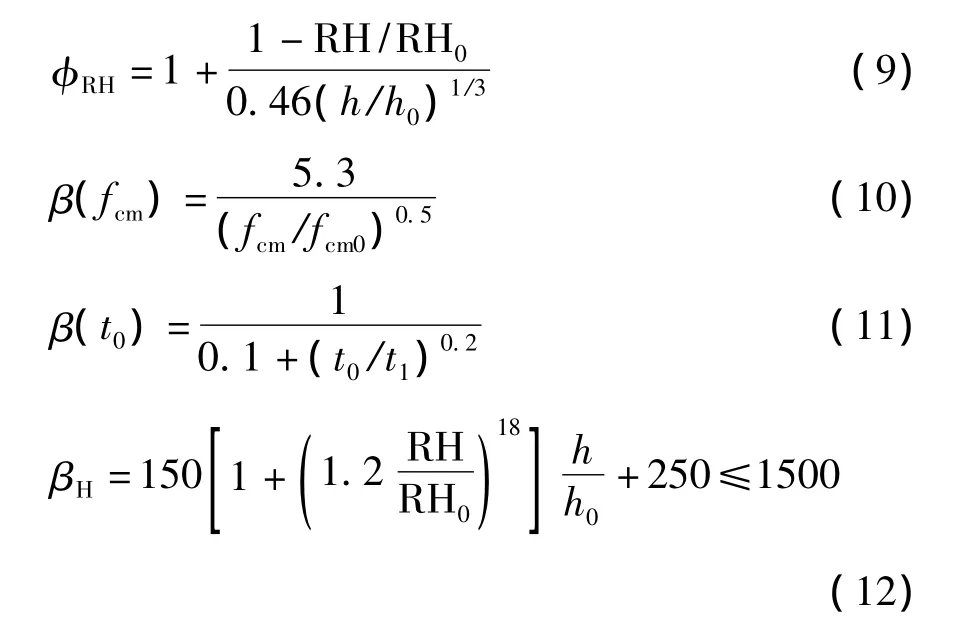
式中有关参数同式(2)～式(5)中的相应参数.

由式(1)－(12)可知，混凝土收缩徐变主要受到5个计算参数的影响，它们分别是混凝土加载时的龄期t0、混凝土开始收缩时的龄期ts、混凝土抗压强度fcm、构件理论厚度h和年平均相对湿度RH.

2 混凝土收缩徐变效应随机分析

响应面拟合技术及蒙特卡罗试验相结合的响应面－蒙特卡罗法可通过以下两个步骤实现［8-9］:

(1)采用数学上的回归拟合技术，通过有限次基于增量有限元法的收缩徐变效应确定性分析，拟合出关于预应力混凝土斜拉桥收缩徐变效应的响应面函数，以逼近真实的收缩徐变效应函数 R=R(X1，X2，…，Xn)，其中 X1，X2，…，Xn为混凝土收缩徐变随机参数.

事实上，第(1)步构造响应面函数时隐含了两个问题，即响应面函数形式和数值试验点的选取.针对预应力混凝土斜拉桥收缩徐变效应随机分析的特点，在变量空间中的高概率密度区域，响应面函数应能很好地逼近真实的收缩徐变效应函数，而且，其形式应尽量简单.

文中关于预应力混凝土斜拉桥收缩徐变效应的响应面函数采用不含交叉项的四次多项式形式［5］:

式中:a、bi、ci、di和 ei(i=1，2，…，n)为待定系数.

显而易见，式(13)中待定系数的个数为4n+1，为确定这些待定系数，需要进行4n+1次数值试验.其中，每一次数值试验对应一个事先选定的试验点，该试验点坐标值即为该次数值试验中收缩徐变参数的取值，通过混凝土收缩徐变效应确定性分析的增量有限元计算，即可获得该试验点对应的收缩徐变效应值.经过4n+1次确定性分析，可得到与4n+1个试验点相对应的4n+1个收缩徐变效应值，从而能完全确定式(13)中的4n+1个待定系数.参考Bucher建议的试验设计方法［10］，试验点的选取坐标为(μX1，μX2，…，μXn)，(μX1± σX1，μX2，…，μXi，…，μXn)，(μX1，μX2± σX2，…，μXi，…，μXn)，…，(μX1，μX2，…，μXi± σXi，…，μXn)，…，(μX1，μX2，…，μXi，…，μXn±σXn)，(μX1± 2σX1，μX2，…，μXi，…，μXn)，(μX1，μX2±2σX2，…，μXi，…，μXn)，…，(μX1，μX2，…，μXi± 2σXi，…，μXn)，…，(μX1，μX2，…，μXi，…，μXn±2σXn)，其中μXi和σXi分别为随机参数Xi的均值和标准差.

3 混凝土收缩徐变效应置信度分析

在预应力混凝土斜拉桥的计算分析过程中，人们通常是基于参数的设计值对结构的收缩徐变效应进行预测.但由于收缩徐变参数自身的变异性，实际发生的收缩徐变效应与设计预期值之间不可避免地存在一定的偏差.事实上，收缩徐变效应是依一定概率取值于某一区间的随机变量.引入区间估计的概念，即可通过置信区间与置信度的概念把收缩徐变效应的可能取值范围与概率联系起来.设收缩徐变效应值的一个置信区间为［R0－Δ，R0+Δ］，其中R0为收缩徐变效应的设计预期值，Δ为置信区间的半宽，则收缩徐变效应值落在该区间外的概率，即显著水平，可表示为

式中:P{·}为事件{·}的概率，

式中:X1，X2，…，Xn为收缩徐变计算参数;R为考虑收缩徐变计算参数变异后的收缩徐变效应实际可能值，R=R(X1，X2，…，Xn).由式(14)和式(15)可知，显著水平α由两部分组成，即

式中:

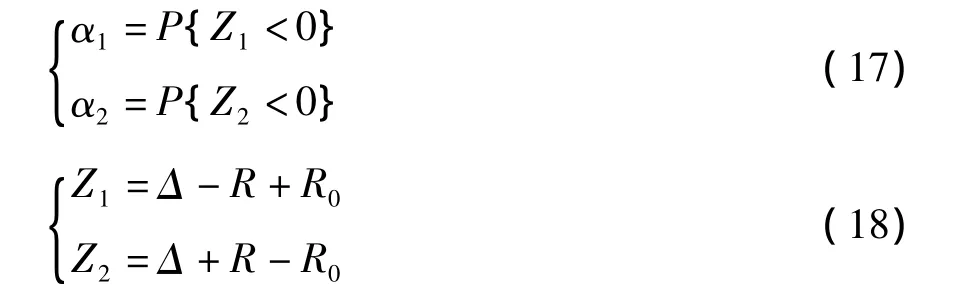
［11-14］，从混凝土收缩徐变的机理来看，混凝土结构收缩徐变效应的随机性是由众多相互独立的偶然因素共同引起的，因此可以合理地假定收缩徐变效应 R=R(X1，X2，…，Xn)服从正态分布，则α1和α2分别为

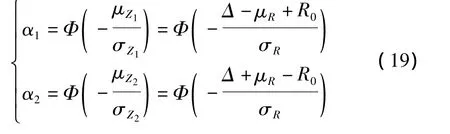
式中:Φ(·)为标准正态概率分布函数;μZ1和 μZ2分别为Z1和Z2的均值;σZ1和σZ2分别为Z1和Z2的标准差;μR和σR分别为R的均值和标准差，它们可以利用第2节的随机分析方法求得.

因此，实际的收缩徐变效应值落在区间［R0－Δ，R0+Δ］内的置信度为

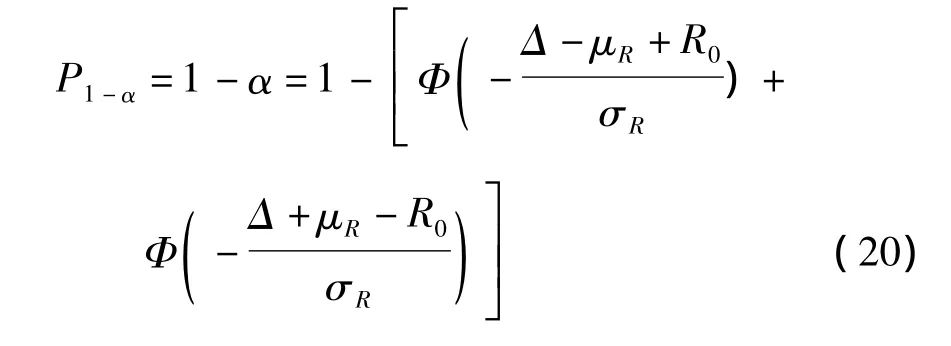
4 甘竹溪大桥收缩徐变效应概率分析

4.1 工程概况

甘竹溪大桥是国道主干线广州绕城公路跨越甘竹溪水道的一座特大型桥梁，为独塔双索面、墩塔梁固结体系的预应力混凝土斜拉桥.大桥主跨跨径为210m，边跨跨径为165 m，边跨设置1个辅助墩，边跨跨径布置为115+50=165 m;主塔采用双直柱式塔柱，桥面以下塔柱(墩)高15.3 m;桥面以上塔柱高101.25m，高跨比 1∶2.07，大桥立面图如图 1 所示.主梁为单箱三室的预应力混凝土扁平箱梁，桥面总宽为38.7m，箱梁中心线处梁高为2.8 m，高跨比为1∶75，高宽比为 1∶13.82，宽跨比为1∶5.43，主梁标准截面如图2所示.主梁标准节段长为6 m，共计48个标准节段，其中，主跨32个，边跨16个;主梁标准节段采用挂篮悬臂现浇的方式进行施工，其余梁段则采用支架现浇方式施工.

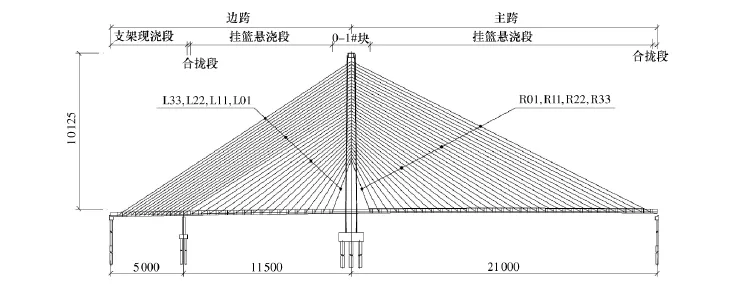
图1 甘竹溪大桥立面图(单位:cm)Fig.1 Elevation of the Ganzhuxi Bridge(Unit:cm)

图2 甘竹溪大桥主梁截面图(单位:cm)Fig.2 Section of the main girder of the Ganzhuxi Bridge(Unit:cm)

4.2 计算参数及其统计特性

由第2节的介绍可知，预应力混凝土斜拉桥的收缩徐变效应受混凝土加载龄期等5种计算参数的影响.在甘竹溪大桥收缩徐变效应概率分析中，将会以这5种参数作为输入的随机参数;根据该桥的实际情况，相应的计算参数共11个，其统计特性如表1所示.

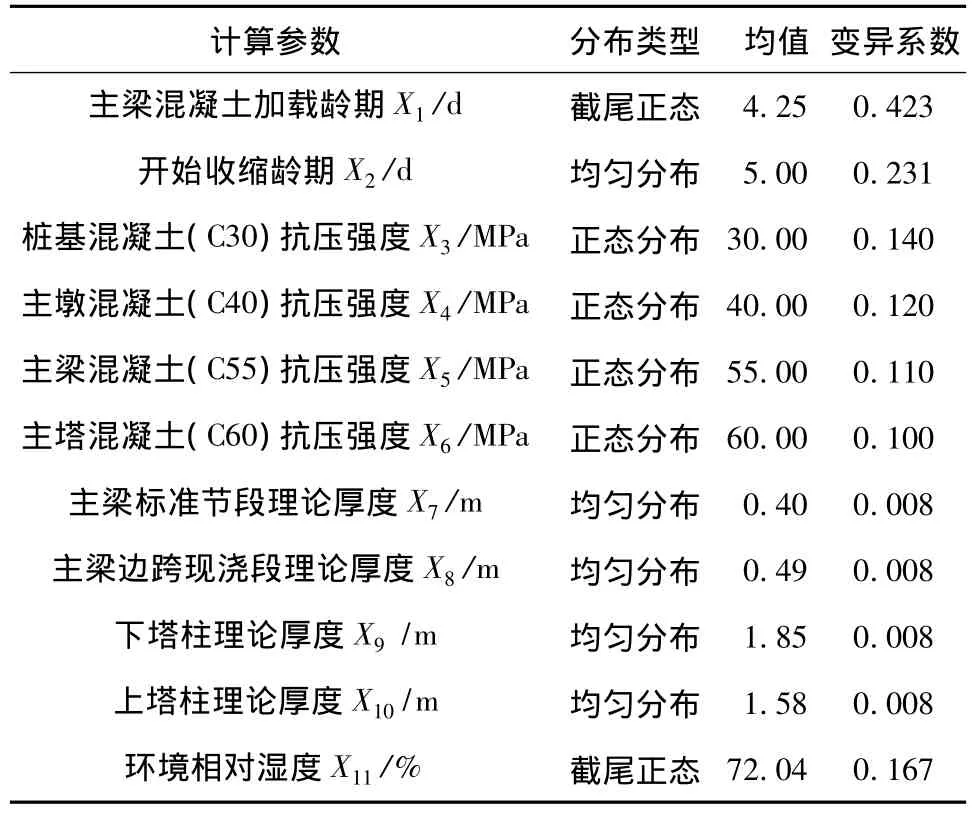
表1 混凝土收缩徐变计算参数及其统计特性［7，12，15］Table 1 Random parameters and their statistical values for calculation of shrinkage and creep effect

4.3 随机分析结果

成桥运营阶段，在经历了施工过程复杂的应力历史后，混凝土收缩徐变将继续发展，桥梁结构的内力和变形将进一步变化.由收缩徐变引起的主梁主跨跨中挠度和斜拉索索力变化是工程人员关心的响应量.考虑混凝土收缩徐变参数的变异性，对甘竹溪大桥进行收缩徐变效应随机分析，可获得由收缩徐变引起的主梁主跨跨中挠度及斜拉索索力的统计特性，见表2、3.表中，设计预期值为收缩徐变参数按均值取值时，收缩徐变引起的挠度值或斜拉索索力值;采用文中方法计算收缩徐变效应的统计特性时，样本数目为5000.

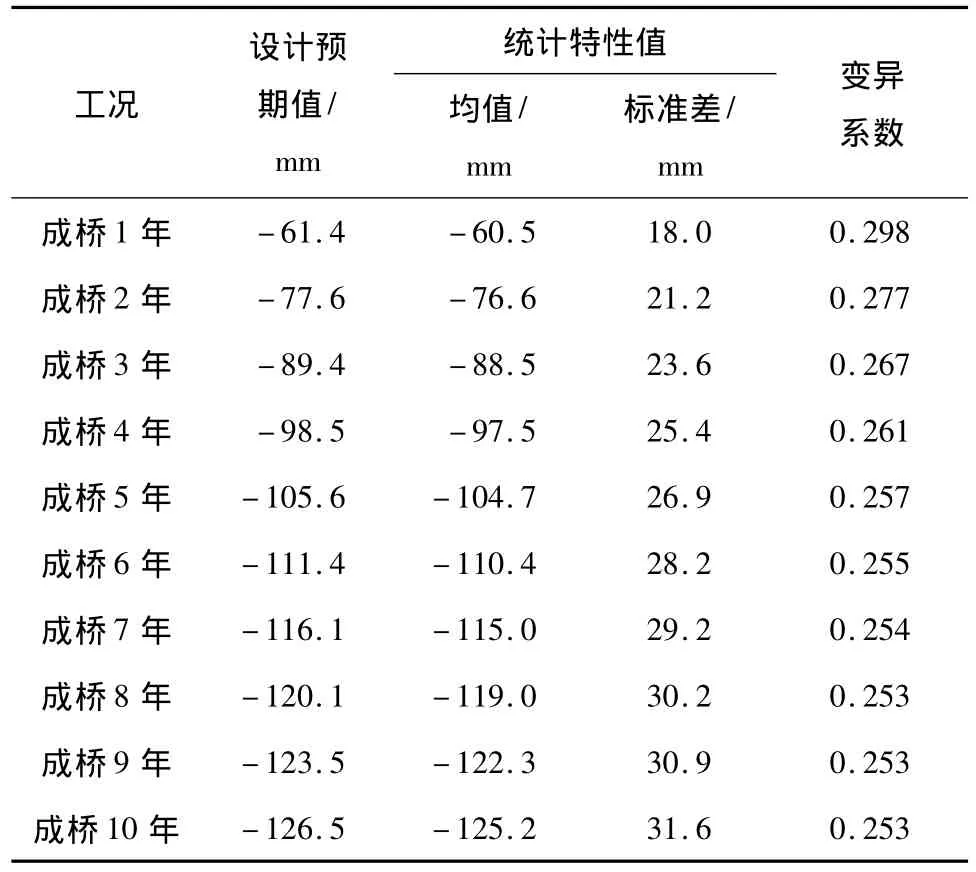
表2 收缩徐变引起的主梁主跨跨中挠度随机分析结果Table 2 Results of stochastic analysis of the mid-span deflection of the main-span girder due to shrinkage and creep

由表2可知，在成桥1～10年的各计算工况中，挠度设计预期值与挠度均值相差较小，说明设计预期值能较好地反映挠度效应的最大可能值.从成桥1年至成桥10年，挠度的标准差不断增大，说明由于混凝土收缩徐变参数的变异，主跨跨中挠度的变异性随时间不断变大.各工况下的变异系数均在0.25以上，说明收缩徐变参数的随机性引起的主跨跨中挠度的变异性是相当明显的，正常施工过程中的收缩徐变参数偏差能使主跨跨中挠度相对于设计预期值产生较大的偏离.

表3给出了成桥及成桥后10年两个工况下由混凝土收缩徐变引起的索力变化随机分析结果，其中的索号所对应的斜拉索如图1所示.从表3可知，两个工况的索力设计预期值与索力均值很一致，说明设计预期值能很好地反映索力效应的最大可能值.成桥后10年索力的标准差比成桥时明显增大，说明随时间的延长，收缩徐变参数变异性的影响增大.另一方面，在两个工况相比较的情况下，索力均值变化量越大，索力标准差增长越多，这说明内力变化越大的斜拉索，其在内力重分布的过程中受收缩徐变的影响越大.

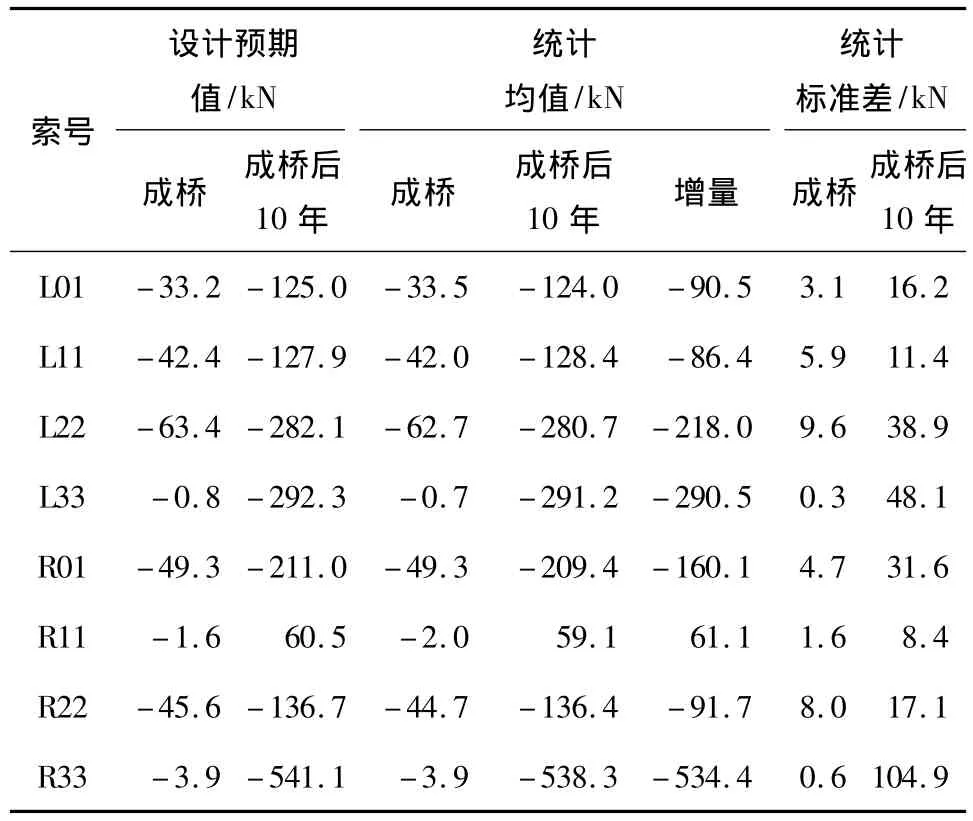
表3 收缩徐变引起的斜拉索索力随机分析结果Table 3 Results of stochastic analysis of cable tension due to shrinkage and creep

4.4 收缩徐变参数分析

基于收缩徐变效应的响应面函数，即式(13)，可计算出只有其中一个参数发生变异时的收缩徐变效应的标准差，以反映该参数对收缩徐变效应统计特性的影响程度.图3(a)、(b)、(c)给出了单个收缩徐变参数变异而导致的主梁主跨跨中挠度及斜拉索索力标准差，据此可评估不同计算参数的影响程度.

由图3可知，各参数对主梁主跨跨中挠度及斜拉索索力的影响程度有所不同.其中，环境相对湿度(X11)的影响程度最大，其次是主梁和主塔混凝土的抗压强度(X5、X6)，而加载龄期(X1)、开始收缩龄期(X2)、桩基混凝土抗压强度(X3)、主墩混凝土抗压强度(X4)及构件理论厚度(X7、X8、X9、X10)的影响程度较小，是次要的计算参数.

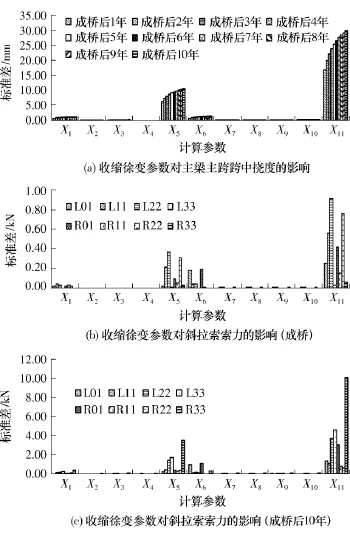
图3 收缩徐变参数对主梁挠度和斜拉索索力的影响Fig.3 Effects of shrinkage and creep parameters on deflections of main girder and cable tensions

4.5 置信区间分析结果

采用前述的置信度分析方法，结合主梁主跨跨中挠度及斜拉索索力随机分析的结果，可以方便地获得收缩徐变效应不同置信区间对应的置信度信息.由式(20)可知，当收缩徐变效应置信区间的半宽Δ取不同值时，其置信度也将不同;反过来，由给定的置信度，也可以求得相应的置信区间.在不同的置信度下，由收缩徐变引起的主梁主跨跨中挠度及斜拉索索力变化量的置信区间分析结果如表4、5所示.

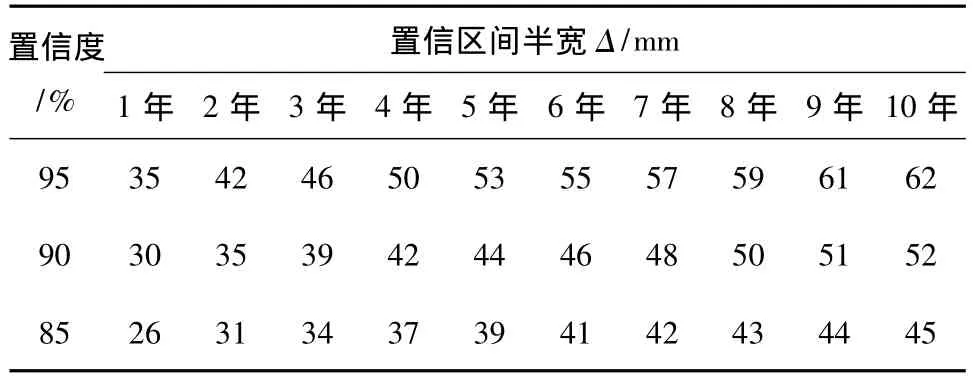
表4 收缩徐变引起的主梁主跨跨中挠度置信区间分析结果(成桥后1～10年)Table 4 Results of confidence interval analysis of the mid-span deflection of the main-span girder due to shrinkage and creep(1 to 10 years after bridge closure)

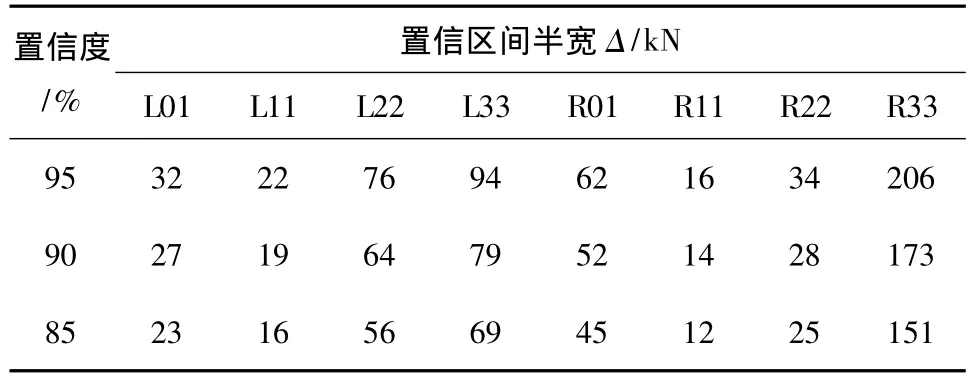
表5 收缩徐变引起的斜拉索索力置信区间分析结果(成桥后10年)Table 5 Results of confidence interval analysis of cable tension due to shrinkage and creep(10 years after bridge closure)

由表4可见，在同一工况下，对于收缩徐变引起的主梁主跨跨中挠度，当给定的置信度越大，其对应的置信区间宽度也越大，例如在成桥后10年，当置信度由85%增大到90%时，其置信区间半宽也由45mm增大到52mm.这说明当置信度要求越高时，收缩徐变引起的主梁主跨跨中挠度的估计区间也越宽.另一方面，在置信度相同的情况下，成桥后的时间越长，由收缩徐变引起的主梁主跨跨中挠度的置信区间宽度也越大，例如在90%的置信度下，置信区间的半宽由成桥后1年的30 mm增大到成桥后10年的52mm.这说明随着时间的推移，收缩徐变的影响越来越大，其变异性引起的主梁主跨跨中挠度的离散性也随之变得更加明显.

由表5可见，到成桥后10年，对于收缩徐变引起的斜拉索索力，当给定的置信度越大，其对应的置信区间宽度也越大，例如对于斜拉索R33，当置信度由85%增大到90%时，收缩徐变引起的斜拉索索力置信区间半宽则由151kN增大到173 kN.这说明当置信度要求越高时，收缩徐变引起的斜拉索索力估计区间也越宽.而对于不同的斜拉索，由于所处的位置各不相同、内力重分配程度大小各异，相同置信度下的置信区间宽度也各不相同，例如在90%的置信度下，收缩徐变引起的斜拉索R11和R33的索力的置信区间半宽分别为14 kN和173 kN，差异相当明显.因此，在进行斜拉索的设计时，为了达到相同的安全水准，不同的斜拉索所需的安全储备应有所不同.

5 结论

预应力混凝土斜拉桥收缩徐变的影响因素众多，各因素的性质复杂多变，因而目前还无法精确分析混凝土收缩徐变引起的结构效应.文中基于我国现行规范JTG D62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》中的混凝土收缩徐变计算模式，考虑其中的影响参数如环境相对湿度、混凝土抗压强度、加载龄期等的随机特性，进行了预应力混凝土斜拉桥收缩徐变效应随机分析和收缩徐变参数的影响程度分析，并进一步对收缩徐变效应的置信度进行了分析.最后，文中把上述概率分析方法应用于国道主干线广州绕城公路甘竹溪大桥收缩徐变效应的分析，获得了一批有价值的数据，并得出了有指导意义的结论.

参考文献:

［1］林元培.斜拉桥［M］.北京:人民交通出版社，2004.

［2］苏成，陈太聪，韩大建，等.崖门大桥主梁牵索挂篮施工模拟计算［J］.桥梁建设，2003(1):12-15.Su Cheng，Chen Tai-cong，Han Da-jian，et al.Simulation calculation for construction with guyed traveler for main girder of Yamen Bridge ［J］.Bridge Construction，2003(1):12-15.

［3］Handa K，Anderson K.Application of finite element metho-ds in statistical analysis of structures［C］∥Proceedings of the Third International Conference on Structure Safety and Reliability.Norway:［s.n.］，1981.

［4］Hisada T，Nakagiri S.Stochastic finite element method developed for structure safety and reliability［C］∥Proceedings of the Third International Conference on Structure Safety and Reliability.Norway:［s.n.］，1981:395-408.

［5］Su C，Luo X F，Yun T Q.Aerostatic reliability analysis of long-span bridges ［J］.Journal of Bridge Engineering，ASCE，2010，15(3):260-268.

［6］苏成，郭奋涛，徐郁峰.斜拉桥索力测量的可靠度研究［J］.桥梁建设，2009(6):27-30.Su Cheng，Guo Fen-tao，Xu Yu-feng.Reliability research of stay cable force measurement of cable-stayed bridges［J］.Bridge Construction，2009(6):27-30.

［7］JTG D62—2004.公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.

［8］庞键.大跨度预应力混凝土斜拉桥收缩徐变效应随机分析与可靠度分析［D］.广州:华南理工大学土木与交通学院，2010.

［9］徐郁峰，苏成，陈兆栓，等.考虑施工过程的异形建筑结构概率分析［J］.建筑结构学报，2011，32(8):120-126.Xu Yu-feng，Su Cheng，Chen Zhao-shuan，et al.Probabilistic analysis of irregular structures with consideration of construction process［J］.Journal of Building Structures，2011，32(8):120-126.

［10］Bucher C G，Bourgund U.A fast and efficient response surface approach for structural reliability problems［J］.Structural Safety，1990，7(1):57-66.

［11］王梓坤.概率论基础及其应用［M］.北京:北京师范大学出版社，2007.

［12］贡金鑫，魏巍巍.工程结构可靠性设计原理［M］.北京:机械工业出版社，2007.

［13］张蓓，殷学纲.随机参数结构的建模技术［J］.重庆大学学报:自然科学版，2000，23(1):45-48.Zhang Pei，Yin Xue-gang.A method of modeling with structuralstochastic parameters ［J］.Journal of Chongqing University:Natural Science Edition，2000，23(1):45-48.

［14］张清华，李乔，唐亮.基于参数识别的结构损伤概率诊断方法［J］.工程力学，2007，24(8):15-21.Zhang Qing-hua，Li Qiao，Tang Liang.A statistical damage assessment method based on parameter estimation［J］.Engineering Mechanics，2007，24(8):15-21.

［15］饶瑞.大跨度混凝土箱梁桥徐变效应研究［D］.广州:华南理工大学土木与交通学院，2009.