一种低信噪比下PSK信号载波频率估计方法

郭 强，吴 杰，桑 睿

(空军工程大学电讯工程学院，陕西 西安 710077)

调制解调系统在信号解调的过程中，发射机与接收机之间的频率偏差会引起载波间干扰，从而导致解调性能严重下降。为了正确地解调信号，必须对载波频率进行高精度估计，使系统达到很好的载波同步［1］。现有的载波频率估计方法主要有过零点检测法、谱估计法、锁相环法［2］。过零点检测法通过测量信号单位时间通过零点的次数计算频率，该方法易于实现，但是易受噪声和直流分量影响。谱估计法分为现代谱估计与直接谱估计。现代谱估计有MUSIC算法估计、AR模型估计与最大似然估计等方法，其特点是估计精度高，但是算法复杂计算量大。直接谱估计(DFT)计算量小，但是估计误差大，算法精度受到信号采样长度N的影响［3］。锁相环法性能良好，但用到电压控制振荡器使得实现结构较复杂，应用难度增大。

本文根据自适应陷波器性质提出一种适应于低信噪比下对PSK信号载波频率估计的方法。仿真证明，该方法能够在低信噪比环境下有效地估计PSK信号的载波频率，提高了载波频率估计精度。

1 信号模型

本文利用自适应陷波器可以将单频干扰滤除的特性，设计了一种可以在低信噪比下有效估计PSK信号的载波频率的方法。如图1所示:本文先将信号进行降噪处理;再通过过零点检测法对信号载波频率进行预估计得到频率f，并建立以f为中心的频率向量F;将F作为自适应陷波器参考频率，得到陷波器输出，计算输出信号能量，根据自适应陷波器滤除单频干扰特性，F中对应能量最小的频率f0即为载波估计频率。为了提高陷波器估计频率的精度，本文采用不断缩小频率向量的分辨率Δf并重复迭代以得到精确稳定的载波频率估计值。

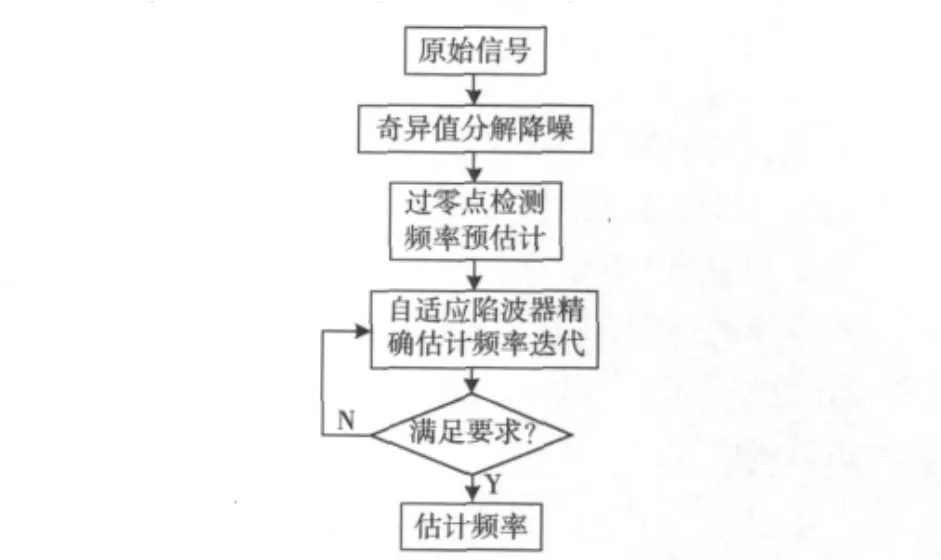
图1 载波频率估计流程图

2 奇异值分解降噪［4］

由于信号的奇异值反映了接收信号中有用信号和噪声的能量分布情况，故可以通过奇异值分解，分析并处理信号的奇异值，从而有效降低信号中噪声的影响。本文利用奇异值分解降噪作为信号的预处理，为之后信号的载波频率估计做准备。

设x(n)，n=1，2，…，N是长度为N的一维信号采样序列，利用此序列可以构造矩阵

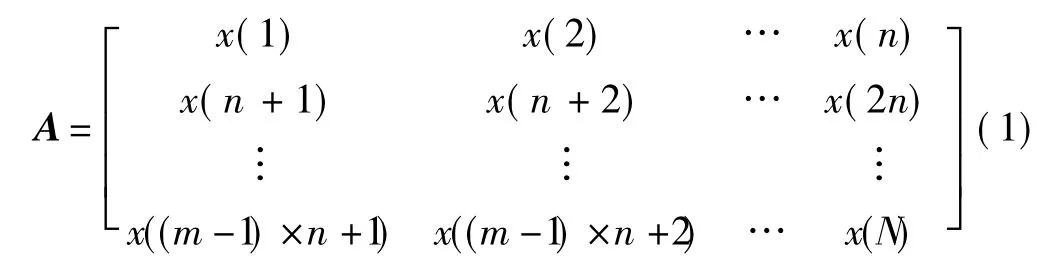
式中:m×n=N，A为m×n维矩阵，秩为R(R≤min(m，n))，对矩阵A进行奇异值分解

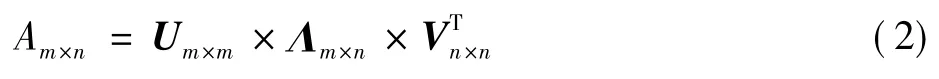
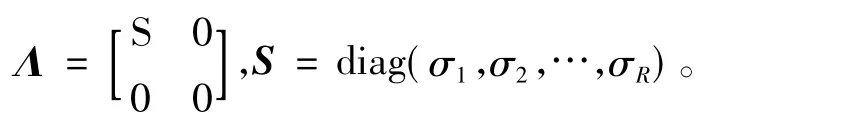
但是如果信号含有噪声，则利用信号的采样序列构造的矩阵A在进行奇异值分解之后得到的m个奇异值关系如

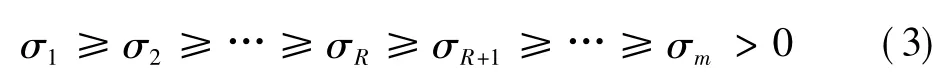
前R个较大的奇异值反映的主要是有用信号，后m－R个较小的奇异值反映的是噪声影响。奇异值分解降噪过程，就是先判决反映有用信号的奇异值R的个数，再将后面m－R个奇异值置零。

令σR+1=σR+2=… =σm=0，构造Λ'如

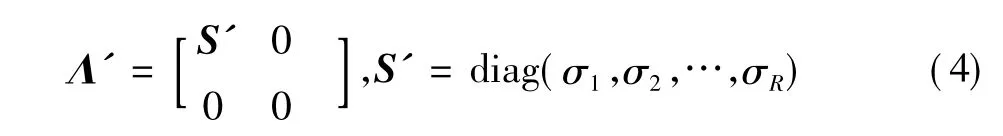
得到新的矩阵Λ'，再利用构造矩阵A的方法反演，得到新的信号采样序列x'(n)。

图2是理想正弦信号在加入白噪声之后，再经过奇异值分解降噪的过程，可以看到，经过奇异值分解降噪的处理，输出信号与原信号基本一致，可以作为后续的载波频率估计的输入信号。

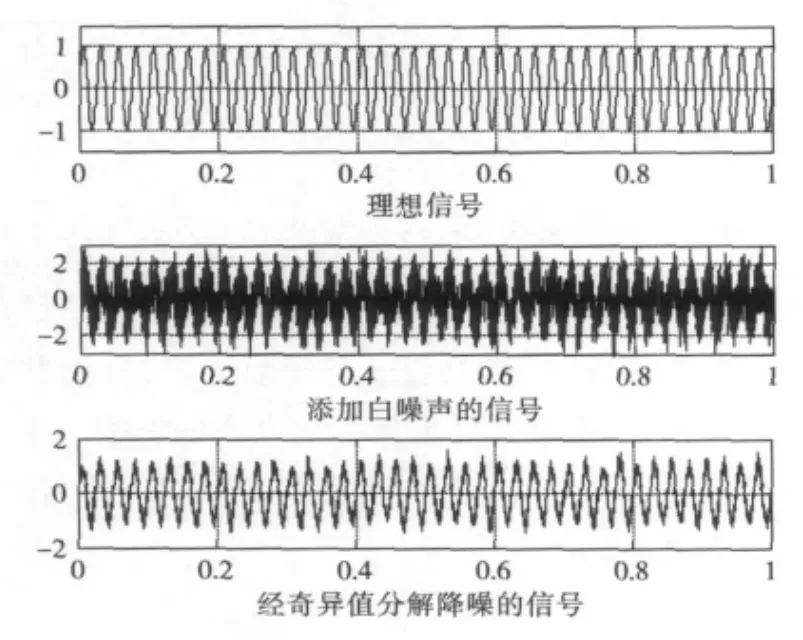
图2 奇异值分解降噪

3 过零点检测对载波频率预估计

过零点检测估计载波频率利用的是周期信号重复通过零点的性质，通过单位时间内对信号通过零点次数的统计，估计出信号的频率。程序实现中利用采样信号的相邻两个采样值之积C进行判断，即当C≥0时判定信号没有通过零点，C＜0时判定信号通过零点。

此种方法受到噪声的影响比较明显，在信噪比较低的环境下，采样信号瞬时信息受到的干扰较大。因此在低信噪比下，过零点检测估计载波频率误差较大。但是信号通过上述的奇异值分解降噪后，再进行过零点检测估计载波频率，则误差会减小很多，可以作为下一步自适应陷波器滤波的参考频率。

如图3所示，对经过奇异值分解降噪之后的信号进行过零点检测估计载波频率的结果，明显比没有经过处理的接收信号的误差小很多，尤其是在低信噪比环境下，经过处理的信号的优势更加明显。

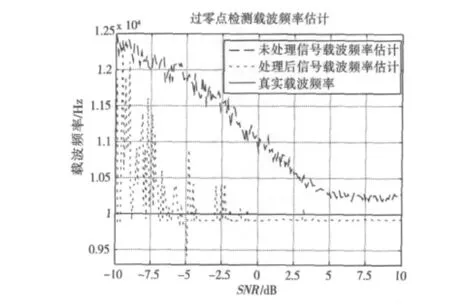
图3 过零点检测估计载波频率

4 自适应陷波器滤波对载波频率精确估计

4.1 自适应陷波器原理

自适应陷波器是自适应对消器的一个应用，其可以抵消掉的干扰是单色干扰(即单一频率的正弦波干扰)。利用这个特性，本文对信号进行陷波器滤波，得到的最小输出能量对应的频率即为载波估计频率［5］。

假设接收的信号中含有单一频率w0的正弦干扰分量Asin(w0n)，即

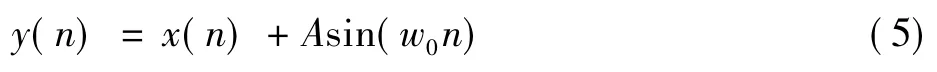
若要消除正弦干扰，需使滤波器满足如下频率特性

这样的系统称为自适应陷波器(简称NF)，又称为点阻滤波器［7］。

为了消除单色干扰，需在参考输入端输入同频率的正弦干扰，并且需要两个权系数的自适应陷波器，分别跟踪干扰的相位和幅度的变化。自适应陷波器工作原理如图4中所示。

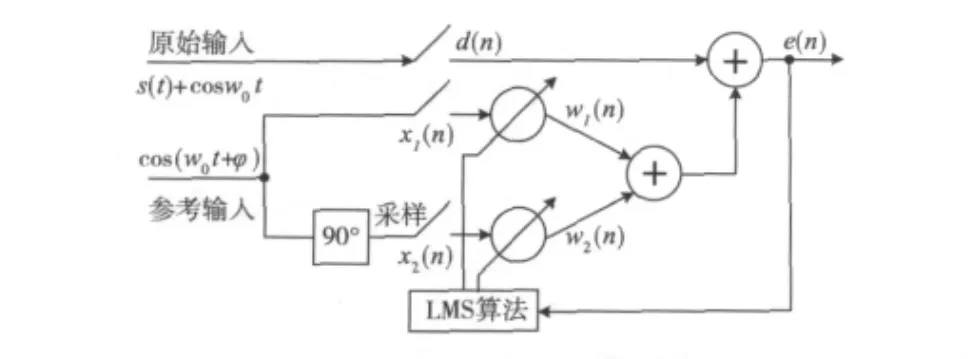
图4 自适应单频陷波器

信号与单频干扰叠加后，送入原始输入端。参考端是一个单频的正弦信号，经过采样后送到x1(n)和x2(n)端，后者经过一个90°相移，系统中的两个权系数的作用是，调整组合后的正弦波的振幅和相角，达到与原始输入端的干扰分量相同的目的，从而实现单频对消［6］。

图5中从频域观察自适应陷波器的工作特点，可见混入的50 Hz的单频干扰信号通过自适应陷波器的处理后基本被抑制掉，输入信号还原成与原始信号频谱基本一致的信号。可见，通过自适应陷波器的处理，可以有效地抑制单频的干扰。

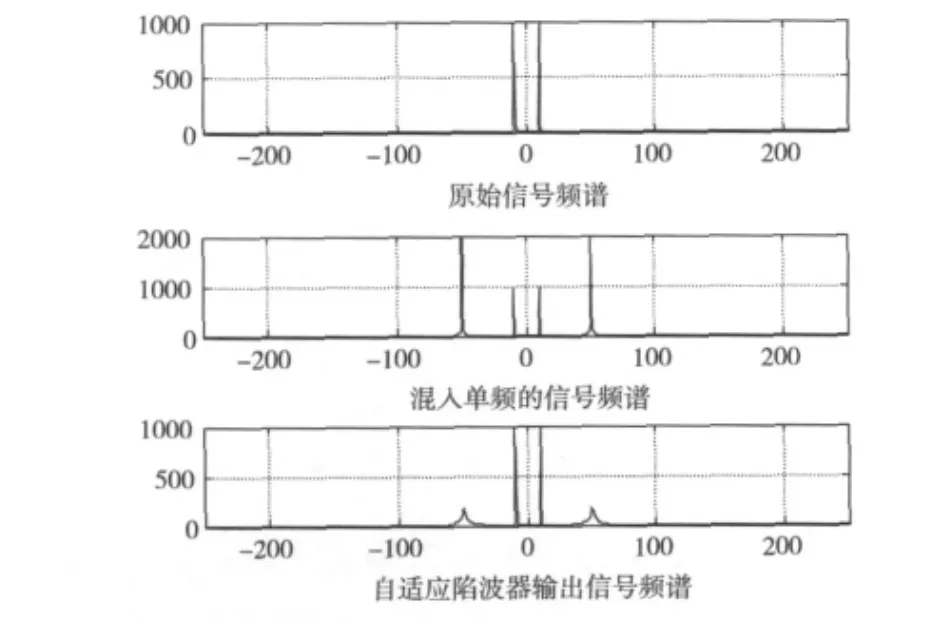
图5 自适应陷波器频域工作过程

4.2 自适应陷波器精确估计载波频率

本文中以过零点检测法得到载波频率的预估计值，作为自适应陷波器的参考频率。但是从上文可以看出，在低信噪比环境下，过零点检测法得到的频率存在一定的误差，这导致自适应陷波器不能够很好地将信号中地载波成分去除，使得到的信号的能量最小，也即对载波频率的估计产生较大误差。

针对此情况，本文设计了一个频率搜索方法，具体过程如图6所示。

1)将过零点检测法得到的估计频率f0作为中心频率建立一个频率向量F1，其分辨率为Δ f。

2)将此频率向量作为自适应陷波器的输入频率，计算每一个频率点对应得到的陷波器输出的能量大小。

3)将最小的能量对应的频率作为下一次迭代的频率向量的中心频率，同时缩小分辨率Δ f，建立新的频率向量F2。

4)重复上面步骤，迭代多次得到精确并且稳定的频率估计值f。

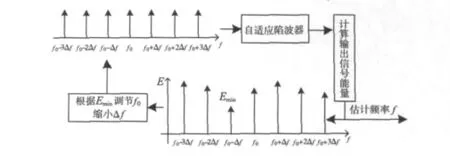
图6 频率搜索过程

5 仿真结果

在所有的仿真实验中，仿真产生的PSK信号载波频率为10 kHz，采样频率为50 kHz，码元速率为2500 baud。

从自适应陷波器原理中可以看出，不同的μ值对陷波器的结果影响较大，图7中对比了不同μ值下陷波器的输出。可以看到当μ值越小的时候，陷波器的输出也越尖锐，就是说陷波器对参考频率越敏感，陷波器的输出效果也越好。所以在之后的仿真中，取μ=0.01。

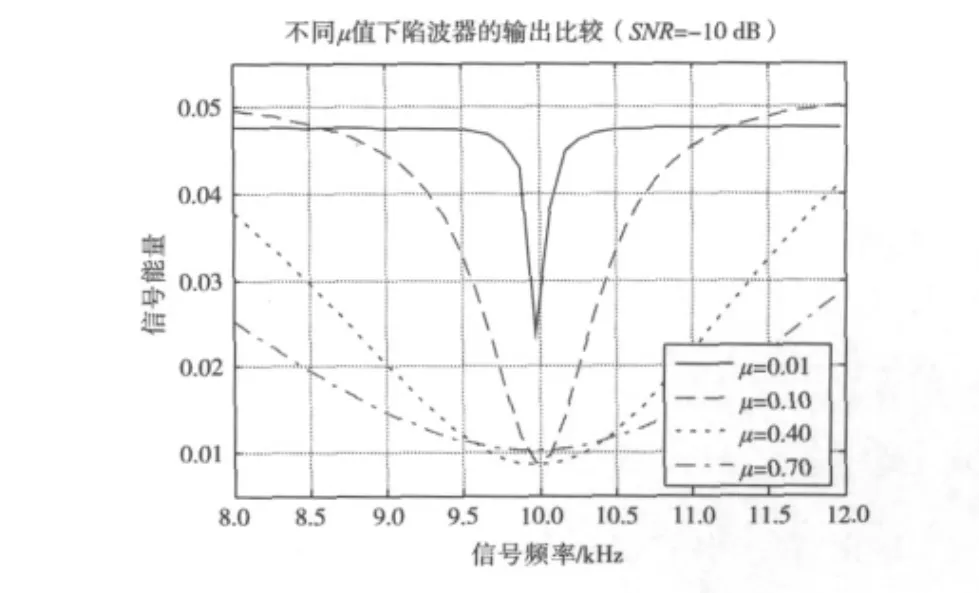
图7 不同μ值陷波器输出对比

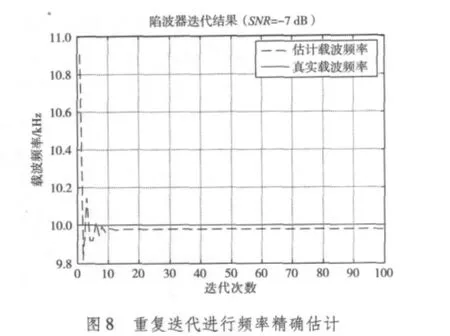
同时，本文中得到精确载波估计频率的重点方法是逐渐缩小频率分辨率Δ f的频率搜索过程，其中迭代次数之间关系到估计频率是否已经稳定。从图8中可以看出，此种频率搜索方法，在迭代次数达到20次时，估计频率已经趋于稳定，所以在之后的仿真中选择迭代次数N=30。

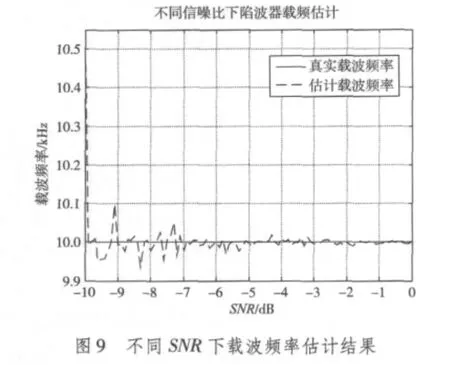
如图9所示，本文在μ=0.01，N=30的条件下对PSK信号载波频率进行估计，在SNR大于－10 dB的环境下，PSK信号载波频率估计偏差不高于1%，在低信噪比下也获得了良好的效果。

6 结论

本文提出了一种基于自适应陷波器的低信噪比下PSK信号载波频率估计的有效方法，并对其性能进行了计算机仿真。结果表明，该方法在低信噪比环境下能够对PSK信号的载波频率进行准确估计，其误差不超过1%。

［1］邹辉，葛建华，王显煜，等.一种TDS_OFDM系统的载波恢复算法［J］.电视技术，2007，31(10):10－12.

［2］刘欢，褚建新，俞万能.改进型自适应陷波器电力系统频率估计方法［J］.上海海事大学学报，2007，28(3):24－27.

［3］朱雪田，彭玉华，周正，等.低信噪比下的提高正弦波频率估计精度算法［J］.电路与系统学报，2001，6(4):103－106.

［4］段向阳，王永生，苏永生.基于奇异值分解的信号特征提取方法研究［J］.振动与冲击，2009，28(11):30－33.

［5］束立红.一种新的正弦信号频率估计方法［J］.仪器仪表学报，2006，27(6):29－31.

［6］邱天爽，魏东兴，唐洪，等.通信中的自适应信号处理［M］.北京:电子工业出版社，2005.

［7］丁玉美，阔永红，高新波.数字信号处理—时域离散随机信号处理［M］.西安:西安电子科技大学出版社，2002.