水下运载器调节索抗流功能的数值计算与分析

王 帅，刘 涛，张文忠

（中国船舶科学研究中心，江苏 无锡 214082）

水下运载器调节索抗流功能的数值计算与分析

王 帅，刘 涛，张文忠

（中国船舶科学研究中心，江苏 无锡 214082）

调节索是从水下运载器悬下的重型链条，能够在运载器悬停于水中时起到辅助抗流的作用。文中给出了调节索实现抗流功能的控制方程，并对方程中用到的运载器纵向阻力系数、垂向运动时的水动力系数及附加质量进行了数值计算，最后给出了调节索长度及重量对运载器抗流调节范围的分析结果。

水下运载器；悬停；调节索；数值计算；辅助抗流

1 引 言

对于军用水下运载器而言，提高隐蔽性和节省能源是影响其实际作战的关键因素。水下悬停具有显著降低运载器噪声、节省电能的优点，因此成为运载器水下停泊的重要方式之一[1]。由于无动力情况下运载器不能自主抵抗海流的作用，可借助悬停装置调节索来辅助抗流，以达到悬停平衡状态。

调节索是从水下运载器悬下的一根重型链条，用于运载器接近海底时调节浮力，其长短由专用绞车收放。调节索的第一次应用是在Piccard设计的深潜器“FNR-3”号上，取得了很好的效果[2]。它的基本功能就是通过调节水中及海底的索链重量达到辅助运载器抗流的作用。

调节索的抗流控制方程中分别用到了水下运载器的纵向阻力系数和垂向运动时的水动力系数及附加质量，目前这三项的计算方法主要有经验公式估算法、CFD数值计算方法、模型试验等。模型试验方法精度最高，但考虑到试验成本高、耗时长，本文采用CFD软件Fluent进行数值计算：模拟运载器在流场中做匀速直航运动得到纵向阻力系数Cx；模拟其沿垂向匀速运动后突变为匀加速度运动，得到运载器垂向附加质量λ33及水动力系数Cz。最后得出了调节索辅助运载器抗流的调节范围。

2 调节索抗流功能的实现

水下运载器需悬停时，一般先降到经济航速工况，以微速航行并进行准确的均衡，然后关闭推进器，再消除零升力Z0(运载器上下对称时Z0=0)、零升力矩M0，以及残存的浮力差和力矩差，使运载器处于静平衡状态。而实际上，均衡总有一定的误差，外界也会对运载器有干扰，如海水密度变化、海流和海面风浪扰动作用等。这些因素可能引起运载器悬停位置的移动以及深度的起伏变化，并伴随不大的纵倾[3]，本文主要考虑海流对运载器悬停的干扰影响。

取右手坐标系O-xyz，坐标原点O位于运载器长度中点，x轴沿纵向指向运载器艏部为正，y轴沿横向指向运载器左舷为正，z轴垂直于水平面向上为正。运载器悬停状态下最常遭受的是斜向海流，如图1所示。当运载器悬停时，通常使其纵向为迎流状态，以最大程度降低运载器在水平面的位置移动，并由艏部侧向推进器进行水平面内的调节。因此文中考虑的斜向海流将分解为垂直面内的纵向海流和垂向海流，两个方向的耦合效应忽略不计。当遭受纵向海流时，通过调节索落在海底的索链重量与海底之间产生的摩擦力来抵抗运载器受到的纵向阻力，其影响因素为海底地质、地貌和运载器的外形。垂向海流是运载器可能遭受的一种极限工况，当运载器接近海底时，依靠接触海底部分的调节索浮力损失与增加来调节运载器的上浮和下潜，最终达到平衡状态。

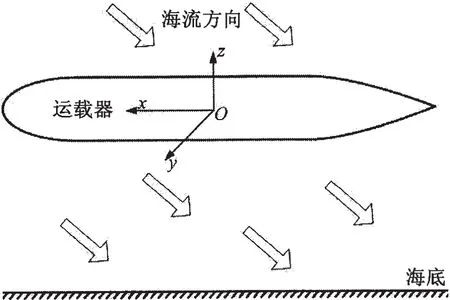
图1 斜向海流示意图Fig.1 Oblique course ocean current sketch map

2.1 纵向抗流

运载器遭受纵向海流时，如图2所示，需要调节索落到海底部分的重量提供的摩擦力不小于运载器所受的纵向阻力。公式表达如下：

式中：Fx表示运载器受到的纵向阻力，f表示调节索与海底之间的摩擦阻力；ρ为海水密度，V0为纵向海流速度，Cx为运载器纵向阻力系数，S为运载器湿表面积，Cf为调节索与海底之间的摩擦系数，Gd为落在海底的单位长度调节索除去浮力后的重量，l为落在海底调节索的长度。

2.2 垂向抗流

若运载器受到垂向海流的作用，如图3为运载器遭受垂直向下海流，调节索的着底节数会自动增减，当一部分调节索着底时，这部分调节索的重量就失去，运载器的浮力增加，当运载器的负浮力等于零时，运载器就能悬停在海底上方一定高度[2]。具体调节过程为：运载器从近底悬停高度H0由零速垂直向下运动，调节索部分节数着底，运载器产生正浮力，加速度减小，而速度逐渐增大，直至运载器正浮力大小与其运动产生的垂向水动力相等，速度达到最大值；之后，运载器由于惯性继续向下运动，其正浮力继续增大，使得速度逐渐降低，直至为0；再后，运载器受正浮力影响向上运动，如此振荡衰减，直至新的平衡位置维持悬停状态。

图2 调节索纵向抗流原理图Fig.2 Simplified schematic of the heavy rope resisting horizontal current

在这个动态平衡过程中，要保证运载器从初始悬停高度开始垂向运动后不能触碰到海底，同时其垂向水动力和调节索水中部分的重力应满足如下关系[4]：

其中，h表示运载器垂向运动位移，w表示运载器垂直运动速度 （向下为正）；M为运载器总排水量，λ33为运载器垂向附加质量，V0为垂直向下海流速度，Fz为运载器受到的垂向水动力，Cz为运载器垂向运动时的垂向水动力系数，Gs为调节索链水中单位长度除去浮力后的重量，H0为运载器初始近底悬停高度。

一般来说，调节索的形式有链状和绳索状等。若选用普通船用锚链，则调节索的单位长度质量m可参照锚链圆钢规格表[5]，由该表得出单位长度调节索质量m和索链直径d之间的函数关系如图4所示，即 m=0.006d2。

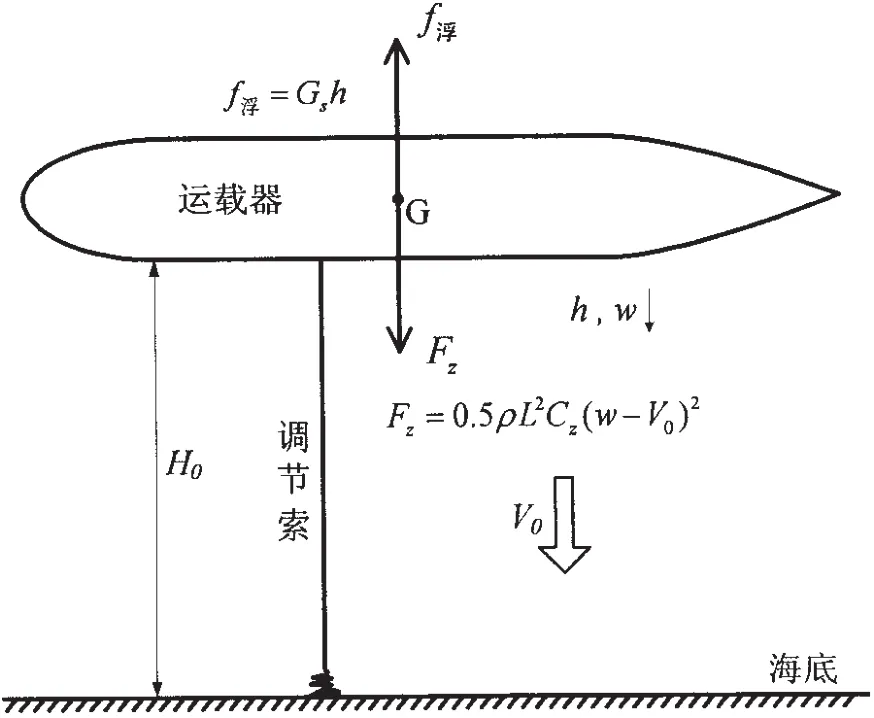
图3 调节索垂向抗流原理图Fig.3 Simplified schematic of the heavy rope resisting vertical current

图4 单位长度调节索质量与索链直径的函数关系Fig.4 Relationship between mass and diameter of the heavy rope per unit length

因此，

其中g为重力加速度值。

3 数值计算过程

3.1 纵向阻力系数Cx

运用CFD软件Fluent 3D求解器模拟运载器在均匀流场中作匀速直航运动，计算区域如图5（a）所示，流场区域的选择应考虑易于结构网格的划分，并且满足边界条件的要求：如出流边界条件要求流动完全发展、不受上游扰动。参考文献[6]选取流场计算域为回转体，回转半径等于运载器长度L，速度进口距运载器艏部为L，压力出口距运载器艉部为2L，取相对压力为0；计算域网格划分为完全结构化网格，正交性好，收敛较快，艉部及近壁面进行网格加密处理，见图5（b）；运载器表面边界条件设定为无滑移静止壁面，流场外边界设定为无剪力静止壁面。

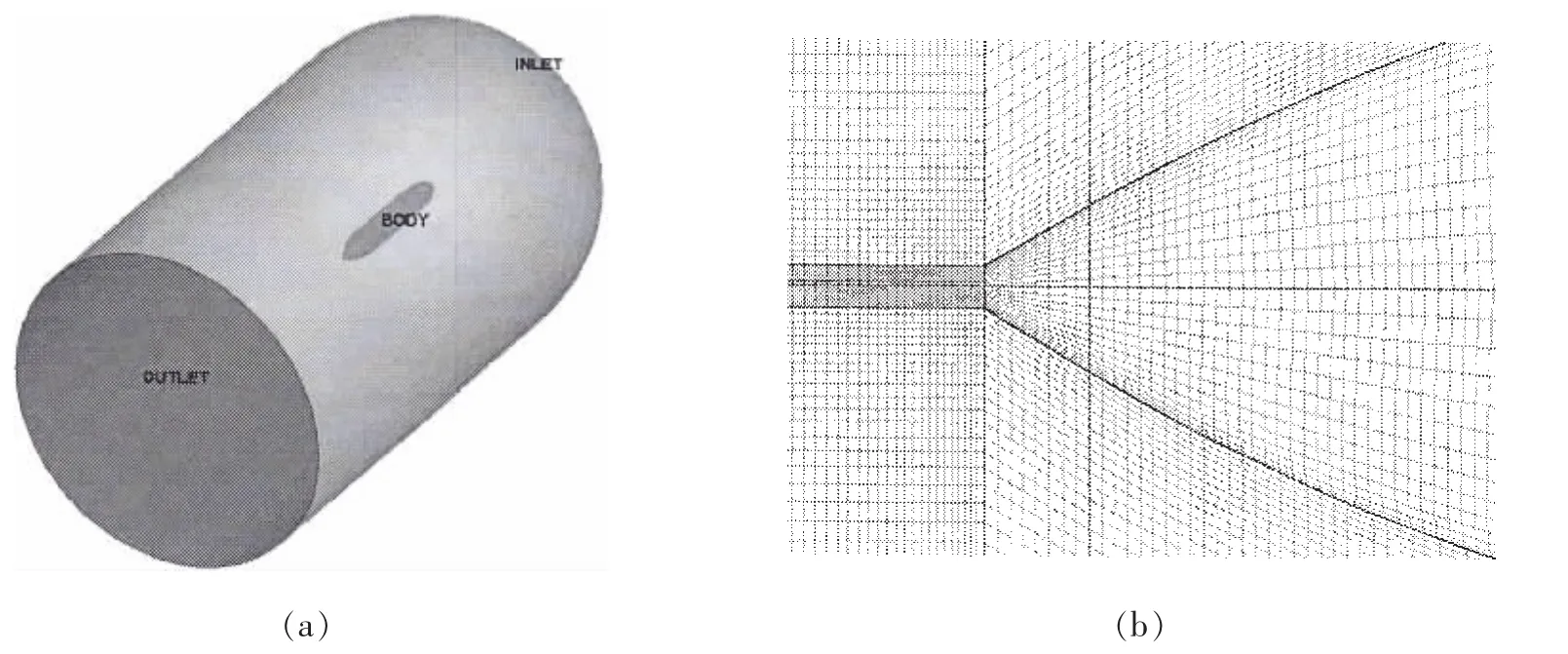
图5 运载器Cx数值计算模型与网格划分Fig.5 Numerical calculation model of Cxand grid mashing of the vehicle

分别模拟速度入口V0=0.6、1.6、2.6、3.6和4.6 m/s对流场进行初始化，方向沿x轴负向，选用RNG k-ε湍流模型对雷诺时均方程RANS进行封闭，压力速度耦合采用SIMPLEC方式，扩散项采用中心差分格式，对流项动量方程，湍动能方程以及湍动耗散率方程的离散均采用二阶迎风格式。监视器残差设置湍动能，湍动耗散率均为1e-9，输入运载器的长度、表面积和流体密度、运动粘性系数等参照值，同时监视运载器壁面沿x方向的阻力系数，迭代得到收敛解，记录运载器纵向总阻力系数Cx，摩擦阻力系数 Cf，粘压阻力系数 Cpv，Cx=Cf+Cpv。

3.2 垂向水动力系数Cz/附加质量λ33

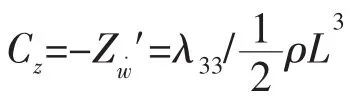
在运载器垂向匀速运动定常计算结果之上，模拟运载器突然以一恒加速度a继续运动，从而带动周围流体一起加速，产生由于运载器加速而引起的附加质量λ33。仍使用2.1节中的完全结构化网格，运用Fluent动网格技术，平动计算使用动态层（Layering）方法。编制用户自定义函数（UDF）程序，其中采用DEFINE_CG_MOTION定义宏确定运载器的垂向加速运动方程，使运载器的壁面在流场中按运动方程运动。计算时，使用收敛性较好的PISO压力耦合方程，取步长为0.000 1s，每一时间步最大迭代100次，监视运载器所受垂向阻力F，初始时会有振荡，经过几个周期后即趋于稳定，图6为a=0.1 m/s2时运载器所受垂向阻力F随时间t的变化情况。读出稳定后运载器所受的阻力F加速，与匀速运动时的阻力F匀速对照，便能计算得到运载器的垂向附加质量，其计算表达式如下：

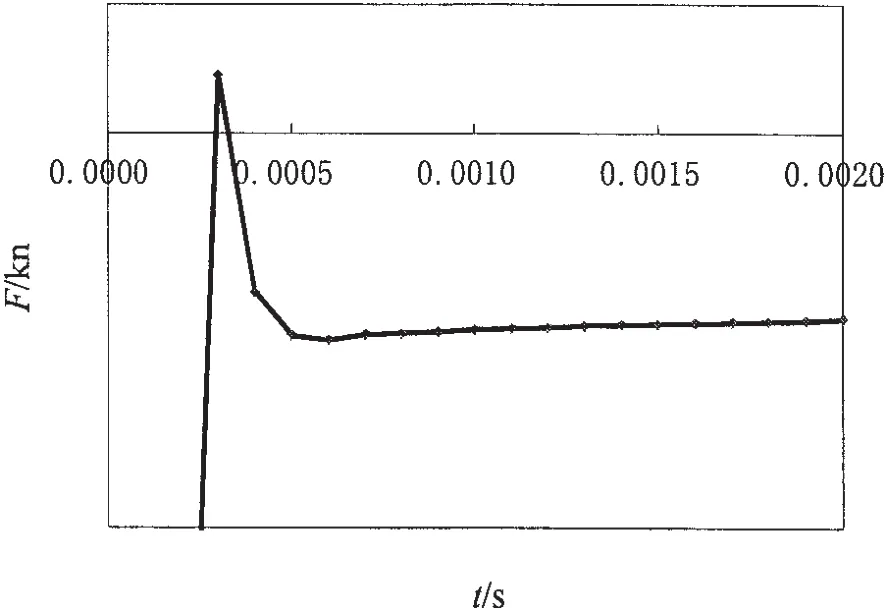
图6 步长为0.000 1 s时运载器垂向加速运动所受阻力Fig.6 Time step size=0.000 1 s,resistance of the vehicle accelerating in vertical direction

4 计算结果与分析

4.1 纵向抗流

表1为运载器匀速直航的纵向阻力系数Cx计算结果。由表中可见数值计算得到的摩擦阻力系数Cf与ITTC平板摩擦经验公式得到的Cf′随航速变化的趋势完全一致，且数值计算结果比经验公式值略小，误差为2%左右。而粘压阻力Cpv只和运载器形状相关，计算结果显示其随航速变化甚微，也验证了数值计算的准确性。图7显示了不同纵向海流速度下运载器所受的纵向阻力Fx的大小。

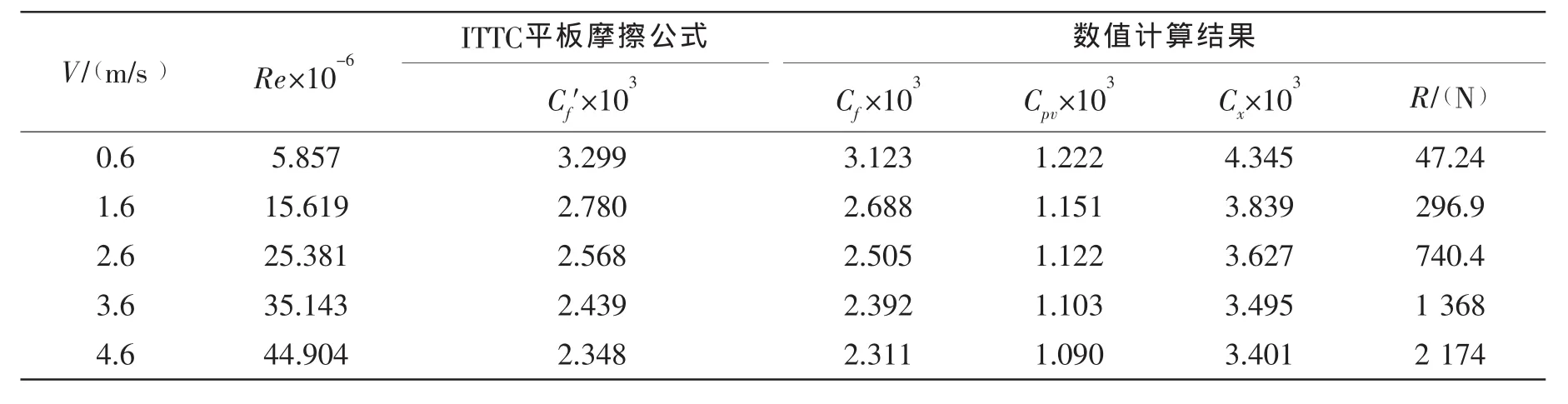
表1 Cx数值计算与公式估算结果对比Tab.1 Comparison between numerical calculation and formula estimation results of Cx

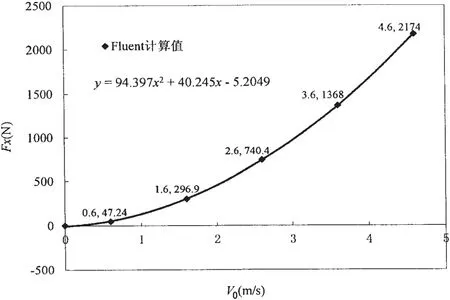
图7 不同纵向海流速度下运载器所受纵向阻力计算值Fig.7 Computation results of traverse resistance of the vehicle under different lateral current velocity

本算例取纵向海流速度 V0=0.5 kns，则 Fx=22.95 N，由公式（1）、（3）可得出：

因此，落在海底的调节索长度l应满足

例如，根据锚链圆钢规格表中的尺寸，取锚链直径d=38 mm时，落在海底的调节索长度l至少应有0.76 m。

4.2 垂向抗流

为求得运载器垂向附加质量及水动力系数，模拟运载器沿垂向以w=0.154 3 m/s匀速运动，读取运载器所受垂向阻力F匀速=106.7 N，数值计算过程与Fx类似，不再赘述。之后模拟运载器突然以加速度a=0.1 m/s2加速运动，读取稳定后的垂向阻力F加速=1 860 N，由此计算得：

根据一般情况下潜艇的附加质量系数经验值，有

数值计算结果与经验值误差在10%以内，精确度尚可。

因此，运载器的垂向水动力系数为：

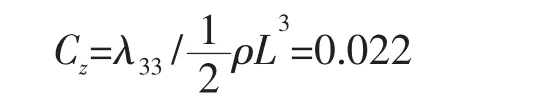
本算例取运载器遭受速度为V0=0.5 kns的垂直向下海流，运载器初始悬停高度H0=10 m，则联合公式（2）、（3），得到下列非线性微分方程

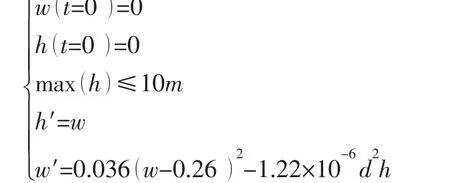
利用Matlab自带的四阶龙格库塔算法容易求出上述微分方程的数值解：锚链直径d分别取不同的值进行求解，发现运载器的垂向位移h随d的增大而减小，正符合调节索单位长度重量变化显示的调节特性，即密度相对较大的锚链调节运载器的垂向运动幅度小，但阻尼振荡频率高，锚链密度小时则特性相反。计算得调节索锚链直径需满足d≥17 mm才能保证运载器垂向调节过程中不会触碰到海底，图8为d=38 mm时运载器垂向位移h和速度w随时间t的历程曲线，与1.2节中分析的变化规律完全相符。从图中可知，此时运载器最终稳定前的最大位移max（）h≈2.2 m，约2分钟后重新达到稳定平衡状态，且稳定后运载器距离海底10 m-1.44 m=8.56 m。

图8 运载器遭受垂直向下海流时垂向位移和速度的时间历程曲线Fig.8 Time history curve of vehicle vertical displacement and velocity while suffering vertical downward ocean current

当运载器又突然遭到垂直向上海流作用时，将向水面方向运动。因此，要求调节索着底部分水中重量不小于运载器垂向水动力大小才能抵抗向上海流影响，即

仍选用调节索锚链直径d=38 mm，则

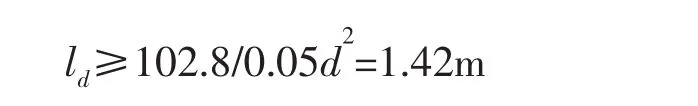
可以看出，针对文中算例，采用调节索装置来克服0.5kns纵向海流和垂向海流影响，要求使用链径为38 mm的锚链长度l总≥l+8.56+ld=10.74 m，取l总=11 m，则调节索总重量约为98.1 kgf，约占运载器全排水量的0.4%，满足调节索设计的一般要求[2]。

5 结 论

本文针对运载器的海流环境要求，阐述了运载器的悬停装置调节索的基本原理和实现过程，并运用数值方法对调节索的长度和重量指标进行了详细的计算，为总体和调节索的相关设计提供依据。基于文中分析结果可得如下结论：

（1）调节索依靠自身重量与海底之间的摩擦力抵抗纵向海流对运载器的作用，其能力还与海底地质情况有关。

（2）调节索辅助运载器实现近底悬停时的反力自协调平衡，主要通过落在海底的调节索重量变化提供或损失浮力来实现。

（3）选择普通船用锚链圆钢作为调节索是可行的，海流速度越大，运载器初始悬停高度越小，需要的锚链直径（密度）越大。

后续的工作中，还将继续分析调节索对运载器小幅纵倾的调节作用，以及收放调节索的速度对运载器的耦合影响等。

[1]潘国良.潜艇悬停及其发展综述[C].中国造船工程学会船舶通讯导航学术会议论文集,2006.

[2]朱继懋.潜水器设计[M].上海:上海交通大学出版社,1992.

[3]何 成,郝英泽,李文龙等.潜艇悬停数学模型的理论探索[J].四川兵工学报,2009,30(2):64-66.

[4]Christina Georgiades,Meyer Nahon,Martin Buehler.Simulation of an underwater hexapod robot[J].Ocean Engineering,2009(36):39-47.

[5]国家质量监督检验检疫总局.GB/T 18669-2002船用锚链圆钢[S].北京:中国标准出版社,2002.

[6]刘 帅.潜艇操纵运动水动力数值研究[D].上海:上海交通大学,2010.

[7]施生达.潜艇操纵性[M].北京:国防工业出版社,1995.

Numerical calculation and analysis of anti-current function provided by a heavy rope on underwater vehicle

WANG Shuai,LIU Tao,ZHANG Wen-zhong

(China Ship Scientific Research Center,Wuxi 214082,China)

A heavy rope hung from underwater vehicle can help resist both horizontal and vertical currents.The control equations which can fulfil anti-current function of the heavy rope were proposed.Numerical calculation of transverse friction factors,vertical hydrodynamic force factors and added mass utilized in the equations when underwater vehicle moves in horizontal and vertical directions was also carried out.Finally,the analysis results of underwater vehicle anti-current adjustable range by different length and weight of the heavy rope were given.

underwater vehicle;hovering;heavy rope;numerical calculation;anti-current aid

U661.3

A

1007-7294（2012）07-0774-07

2011-05-21

王 帅（1988-），女，硕士研究生；刘 涛（1967-），男，中国船舶科学研究中心研究员。