基于OpenFOAM的船舶与液舱流体晃荡在波浪中时域耦合运动的数值模拟
2012-06-22李裕龙朱仁传缪国平陆志妹
李裕龙,朱仁传,缪国平,范 菊,陆志妹
(1上海交通大学 船舶海洋与建筑工程学院,海洋工程国家重点试验室,上海200240;2中国船舶及海洋工程设计研究院,上海200011)
基于OpenFOAM的船舶与液舱流体晃荡在波浪中时域耦合运动的数值模拟
李裕龙1,朱仁传1,缪国平1,范 菊1,陆志妹2
(1上海交通大学 船舶海洋与建筑工程学院,海洋工程国家重点试验室,上海200240;2中国船舶及海洋工程设计研究院,上海200011)
波浪中载液船舶运动激励舱内液体的晃荡,舱内液体晃荡产生的冲击力同时作用在舱壁上,进而影响船舶的运动姿态。波浪中船体水动力和时延函数是在势流理论范畴下采用切片法和脉冲响应函数方法计算获得的,液舱内液体非线性晃荡是基于粘性流理论实时计算模拟,两者耦合建立了波浪中载液船舶与液舱流体晃荡耦合的运动方程。论文基于开源CFD开发平台OpenFOAM,自主开发实现了船体运动与液舱晃荡的耦合计算程序,并进行了相应的数值模拟计算和验证工作。该方法完整地考虑了波浪、船体和液舱晃荡之间的耦合作用,并结合船体内外流场特点分别采用了势流和粘性流理论,具有较高的计算效率。通过数值模拟计算和模型实验研究表明,数值模拟计算能够清晰显现出液舱晃荡对船体全局运动影响,船体运动计算结果与模型实验结果吻合良好。
OpenFOAM;液舱晃荡;脉冲响应函数;运动耦合;时域模拟
1 引 言
船舶在波浪上的运动激励液舱内的液体产生晃荡,液舱晃荡诱导的冲击力同时作用在舱壁上,进而影响到船舶的运动姿态。船舶在波浪上运动与液舱晃荡之间的耦合效应需要在船舶设计阶段给予重视。船舶运动与液舱晃荡之间的耦合效应研究一直是船舶与海洋工程界一直关注的问题,合适且高效的理论与数值计算方法对探讨分析船舶运动与液舱晃荡之间的耦合效应是十分重要的。目前国内外许多学者也就船舶运动与液舱晃荡之间耦合效应进行了分析与研究工作,如Kim[1],Rognebakke和Faltinsen[2-3],以及Newman[4]等,综合来说,耦合效应的相关研究主要可分为两种途径:用线性化理论假定液舱晃荡液体运动的频域计算方法(如Newman[5]),以及用非线性理论进行液舱晃荡流体运动模拟的时域计算方法(如Kim[6-7])。从现有的研究结果来看,采用船舶运动的线性理论方法基本能够满足船舶运动与液舱晃荡之间耦合效应分析研究的要求。
船舶在波浪上的运动计算是船舶与海洋工程领域的经典问题。如果考虑到晃荡流体的非线性作用,则需要在时域下来分析船舶运动。如果采用时域三维Rankine源边界元方法,会需要较长的计算时长,计算效率偏低,不甚适合在时域下进行较长时间的数值计算工作,因此船舶运动与液舱晃荡之间耦合效应的分析研究工作需要更加高效的数值计算方法。本文对船舶运动的时域分析采用脉冲响应函数(IRF)方法。考虑到船舶运动问题的线性化假定,使用脉冲响应函数方法已经能够满足船舶运动与液舱晃荡之间耦合效应的相关研究及分析工作。时域下脉冲响应函数方法需要对频域下的数值计算结果进行傅里叶变换,因此在时域下进行船舶运动计算之前,需要预先得到相关船型的频域计算结果。本文船体频域运动计算采用了基于线性频域势流理论的STF切片法。
液舱流体晃荡问题在学术界与工程界中同样是经典的水动力学问题。自从LNG,LPG等载液高附加值船舶的迅速发展,液舱流体晃荡业已成为水动力学研究工作的热点问题。已有很多学者分别采用了频域势流理论、时域非线性势流理论和粘性流理论方法来研究模拟液舱晃荡问题及其诱导的水动力砰击载荷。本文采用粘性流理论方法,计算的适应性更强,液舱内非线性流体晃荡运动的模拟更为真实。
OpenFOAM是由C++编写的面向对象的开源CFD程序库,它的核心代码主要是基于有限体积法求解偏微分方程系统。OpenFOAM的开放性、完全面向对象的程序设计和完善的分层框架构建,使用户只需花费较少的时间便可开发新的模型和求解器。目前国际上基于OpenFOAM开发并解决工程实际问题已渐渐成为工程界和学术的重要研究热点,但在国内学术与工程领域关于OpenFOAM的研究工作仍属于起步阶段。
本文将船舶在波浪上的运动问题和液舱内液体晃荡问题采用不同的理论求解,船舶的运动采用STF切片理论方法,其中船体的水动力系数预先采用线性频域理论计算,进而使用脉冲响应函数方法获得描述船舶在波浪上时域运动方程中的记忆函数和时域波浪力。应用粘性流理论方法求解非定常液舱流体晃荡问题时采用了有限体积方法计算模拟晃荡流体的非线性现象,其中自由面的捕捉采用了VOF法,计算获得的流体晃荡对舱壁作用力和力矩实时添加至船舶时域运动方程,从而建立了载液船舶在波浪上运动的时域运动方程。本文在开源CFD开发平台OpenFOAM基础上,自主开发实现了基于势流理论的船体运动和粘性流CFD计算的时域耦合,形成了船体运动与液舱晃荡的全耦合计算方法和数值计算程序。这种方法针对船体外流场和液舱内流场的特点分别采用势流和粘性流理论方法,计算速度快,效率高。通过对加载两个液舱的LNG船模进行耦合运动的数值模拟及其相应的模型试验研究表明,数值模拟计算能够清晰显现出液舱晃荡对船体全局运动影响,船体运动计算结果与模型实验结果吻合良好,同时也验证了本文方法准确高效。
2 载液船舶耦合运动相关基本理论
2.1 载液船舶在波浪上的运动
航行船舶的运动计算所采用的参考坐标系oxyz如图1所示,oxy平面与静水面重合,oz轴垂直向上,在规则波激励下船舶保持定速U0航行并作六自由度运动。
本文采用势流理论求解船舶在波浪上的运动。这里给出加载液舱的船舶在波浪上运动满足的数学模型。线性入射波速度势有以下形式:
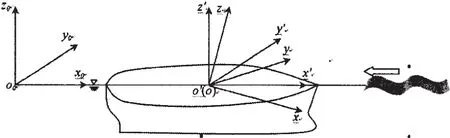
图1 坐标系示意图Fig.1 The coordinate system
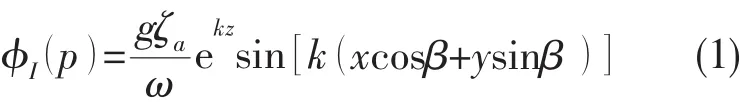
本文采用STF切片法求解外域流场的速度势函数。切片理论实质上是一种近似方法,它充分利用了船体细长这一特点,认为至少在船体的相当部分,流动主要局限于横向截面内,从而把围绕船体的本质上的三维流动简化为绕各横截面的二维流动。按二维流动求得各横剖面遭受的流体作用力后,再沿船长方向迭加(积分)以求得船体上总的流体作用力,该理论的提出约有60年的历史,求解船舶在波浪上运动计算效率高速度快,特别是STF法出现以后,适应范围和准确性有较大提高,很受船舶设计、性能研究和工程应用人员喜爱。STF法更多的详细介绍可见参考文献[8],中文理论介绍也可见刘应中、缪国平所著教材[9]。在二维频域理论假设下,船舶某一剖面运动辐射问题速度势所满足的流场定解条件如下:
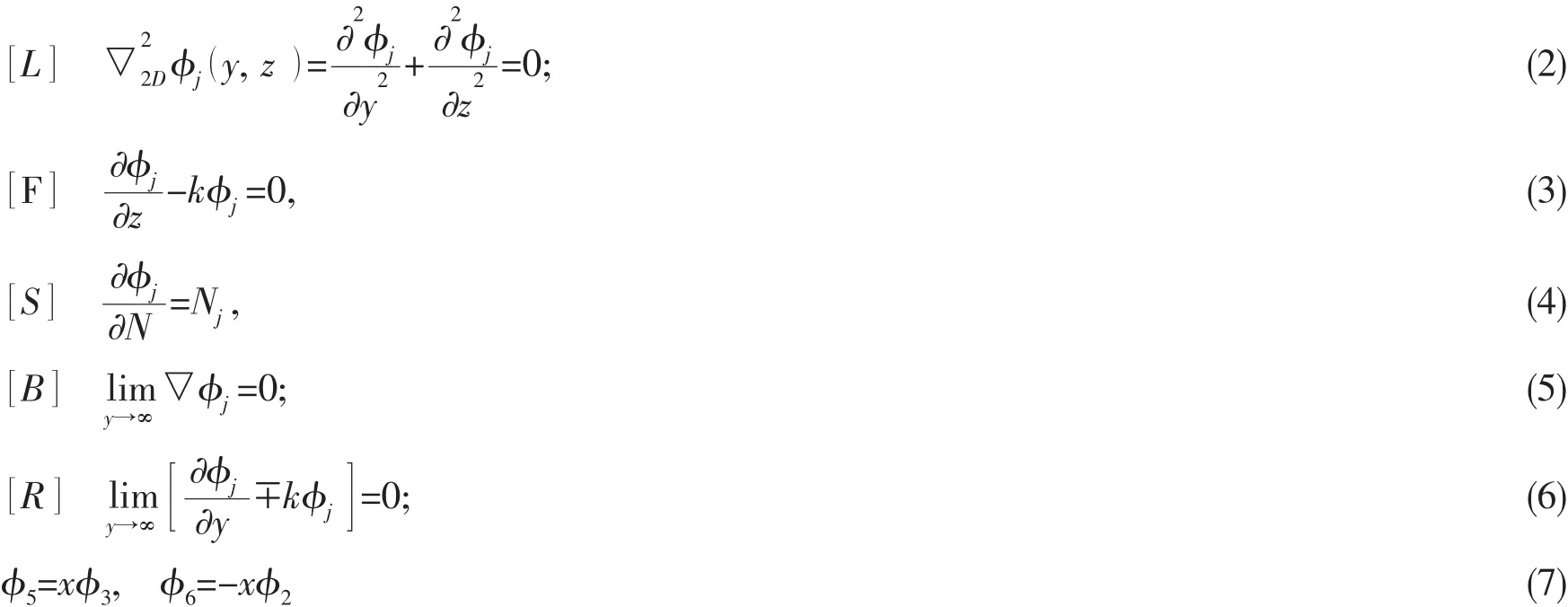
公式(4)中Nj为船体表面的法向矢量,公式(6)中k为波数。本文采用二维无限水深频域格林函数方法求解二维频域理论下船舶外域流场速度势。二维无限水深频域格林函数公式如下:
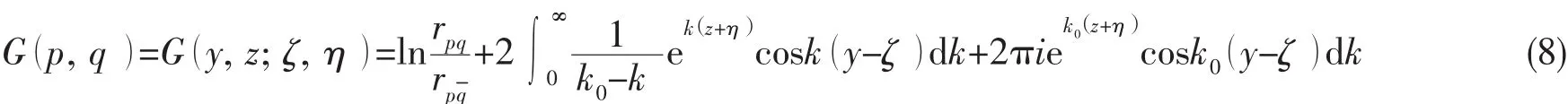
基于频域切片理论的船舶五自由度运动方程如下:

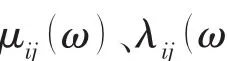
ω 为作用在船体上的广义波浪力。j=2,3,…,6,分别对应的运动模态为横荡、垂荡、横摇、纵摇和艏摇。切片法不能计及船体纵荡运动。
2.2 基于粘性流理论的液舱晃荡问题
本文采用粘性流理论求解液舱内非定常流体晃荡运动,采用了有限体积方法计算模拟晃荡流体的非线性现象。基于粘性流理论假定,液舱内部流场在连续性方程和动量方程的控制下。在直角坐标系下,连续性方程和动量方程分别为:
假设液舱内液体不可压缩,连续性方程和动量方程形式如下:

上式中,i,j=1,2,3;ui,uj为速度分量;p 为压力;ρ为流体的密度;ν为流体的运动粘性系数。 动量守恒方程式(11)写成矢量形式如下:

OpenFOAM对方程(12)的不同微分项分别进行处理,写成如下代码进行计算:

代码中每一行分别与(12)式中的每一项相对应;rho→ρ;mu→μ;phi→φ=ρU 。
液舱内流场自由液面的变形采用VOF方法来捕捉,VOF因子满足的方程形式如下:


公式(14)中定义的边界条件表示在靠近舱壁处流体需满足壁面无滑移条件。这里=u1,u2,u3{ }。在数值计算过程中使用动网格技术模拟液舱随船体的全局运动。为了准确重建自由液面以及描述非线性现象,需要在液舱壁面与自由液面附近划分高质量与较高密度的计算网格。
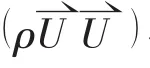
2.3 基于脉冲响应函数方法的船舶运动时域计算
在线性系统中,任意激励可以写为脉冲响应函数和激励的卷积积分形式[8]:)

式中,x(t)为在输入h(t)下的系统响应,F(t)为单位脉冲输入下的脉冲响应函数。将以上概念推广到船舶运动问题,相对于基于频域理论的公式(9),时域船舶运动方程有着如下形式:

式中,Mij,μij(∞ )和Cij分别代表载液船舶质量,无穷大遭遇频率的附加质量以及船舶回复力系数。Kij(t)为时延函数,FWi(t)为作用在船体上的外部时域波浪力。b41和b42为考虑粘性作用的非线性船舶横摇阻尼系数,可以用经验公式,实验或者CFD方法来获得。
时延函数与无穷大遭遇频率附加质量的计算公式为:

上式中,λij(ω)为频域下的水动力阻尼系数,时延函数可以用频域下阻尼系数计算求得;φ( p,∞ ) 为二维剖面无穷大频率下的船舶辐射速度势;μij(∞ )为无穷大频率下船体附加质量。在求解运动方程时在横荡与首摇模态的运动中,本文采用数值弹簧技术来抑制横荡和首摇模态的计算慢漂现象。数值弹簧可以考虑作为一个锚泊系统。各运动模态中弹簧的刚度可表示为:
其中周期Ti远大于波浪激励周期。
3 载液船舶在波浪上时域运动的数值算法和计算流程
在液舱晃荡问题的非定常计算求解过程中,每一时刻舱壁面的压力积分可得到当前时刻下晃荡液体在舱壁上的作用力。这种晃荡流体的水动作用力会直接影响到船舶的运动姿态,因此载液船舶时域运动方程需要在当前时间步下耦合建立。耦合液舱流体晃荡作用的时域船体全局运动方程如下:
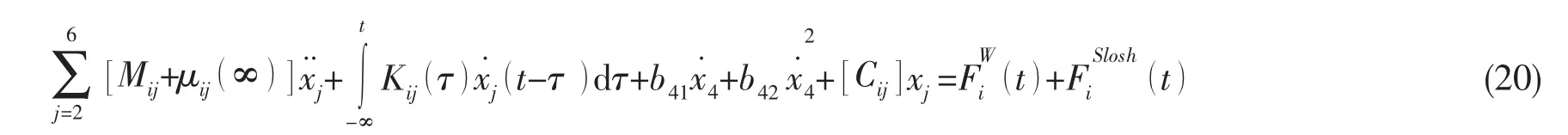
在当前时刻计算求解液舱晃荡问题后,可以得到晃荡液体对舱壁诱导的力和力矩。按照公式(20),将晃荡液体诱导的力和力矩添加至船舶时域运动方程,在当前时刻下求解耦合时域船舶运动方程便可得到船舶运动时历。之后再将船体运动作为下一时刻液舱晃荡问题的壁面边界条件,继续下一时刻计算求解液舱晃荡问题。重复以上过程,在时域下耦合液舱晃荡的船舶全局运动求解方法就建立了。上述时域耦合数值计算方法的详细计算流程可见图2。
这里需要注意,船舶运动方程的力(矩)是基于船舶运动重心位置确定的,转换液舱力(矩)至船舶运动方程以及将船舶运动响应转换至液舱晃荡壁面边界条件时,需要根据船舶的实际装载状况确定船舶与液舱的空间位置关系,同时也须注意处理晃荡诱导力(矩)中的惯性成分。上述基于势流理论的船体运动和粘性流CFD计算的时域耦合工作是在开源CFD开发平台OpenFOAM上编制程序实现的。

图2 耦合数值计算程序流程图Fig.2 Flow chart of numerical calculation program
4 数值计算
4.1 加载液舱LNG船模主尺度与时延函数计算
模型实验是在中国船舶与海洋工程设计研究院的海洋工程水池里进行的,模型实验是针对一条只加载两个菱形液舱的LNG船进行的,实际船舶与模型的缩尺比为68:1,LNG船主尺度见表1。
两个液舱模型形状与主尺度均相同,液舱横剖面示意图见图2,液舱安放位置见图3。液舱长度为585 mm,宽度为638 mm,深度为432 mm。两个液舱分别布置在距船舯处船艉方向152 mm处与距船舯处船艏方向552 mm处。
为了计算求解耦合液舱晃荡影响的时域船舶运动,本文首先使用STF切片法获得了加载液舱的LNG船模的频域计算结果,进而利用脉冲响应函数方法获得时延函数计算结果。部分时延函数计算结果见图4。

表1 LNG船模主尺度Tab.1 Principal dimensions of LNG

图3 液舱横剖面示意图Fig.3 Cross section of the liquid tank
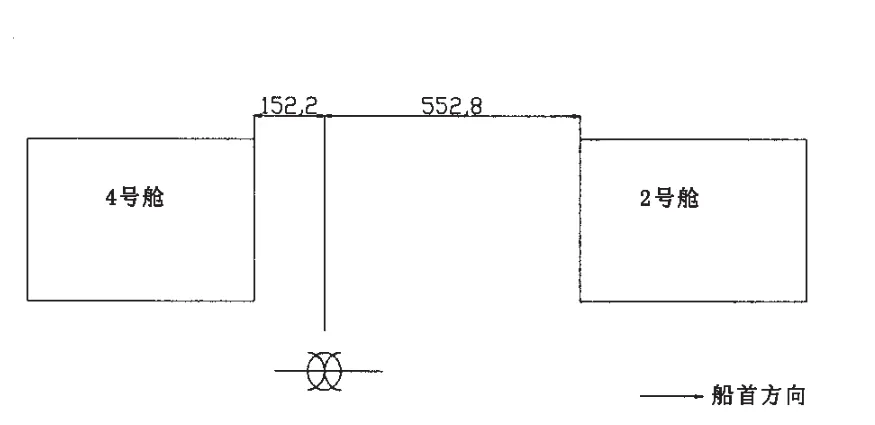
图4 液舱布置示意图Fig.4 Configuration of the liquid tank
4.2 耦合液舱晃荡船舶时域运动的数值计算
将LNG船模频域计算结果转换时延函数和波浪力后,便可在时域下求解耦合液舱晃荡的船舶运动。根据LNG船模试验工况,船模在规则波激励下作六自由度运动,液舱装载液体为水,装载高度为液舱深度的65%。耦合运动数值计算在初始时刻下的液舱自由液面见图5,LNG船模实验时波浪频率范围为0.35至0.45 rad/s。

图5 垂荡与纵摇模态时延函数计算结果Fig.5 Retardation functions of heave and pitch

图6 耦合运动初始时刻液舱自由液面Fig.6 The snap shot of tank sloshing coupling with ship motion

图7 迎浪下垂荡运动时间历程(周期=2.70 s,波幅=2.35 cm)Fig.7 Time history of heave motion(Head sea,T=2.70 s,ζa=2.35 cm)

图8 迎浪下纵摇运动时间历程(周期=2.70 s,波幅=2.35 cm)Fig.8 Time history of pitch motion(Head sea,T=2.70 s,ζa=2.35 cm)
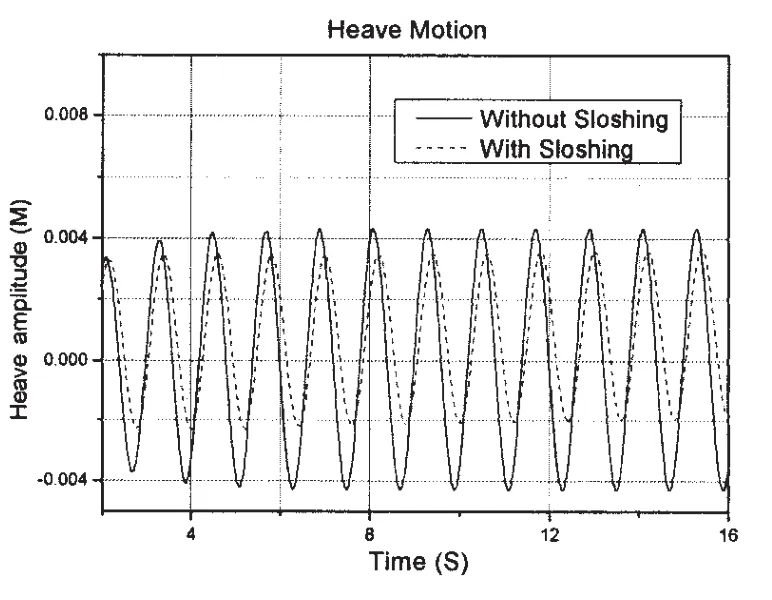
图9 迎浪下垂荡运动时间历程(周期=1.20 s,波幅=2.28 cm)Fig.9 Time history of heave motion(Head sea,T=1.20 s,ζa=2.28 cm)
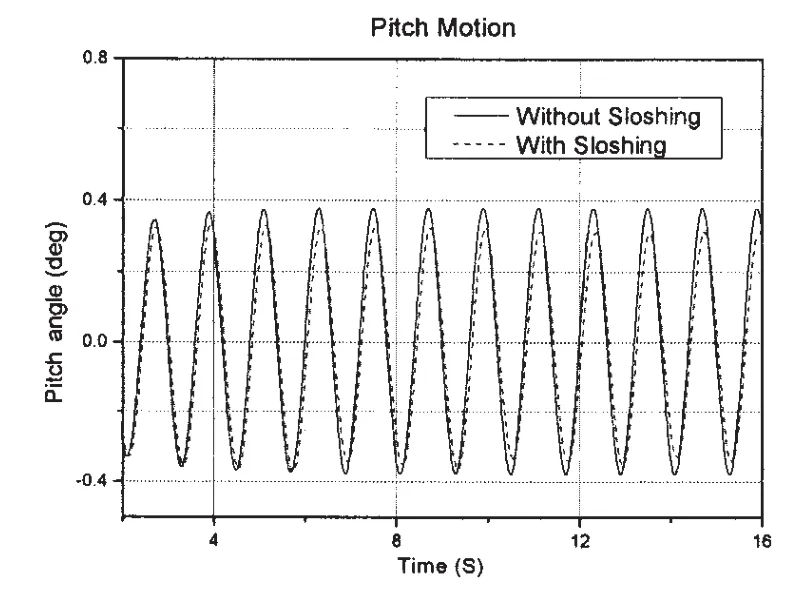
图10 迎浪下纵摇运动时间历程(周期=1.20 s,波幅=2.28 cm)Fig.10 Time history of pitch motion(Head sea,T=1.20 s,ζa=2.28 cm)
图7~12为载液LNG船模在波浪激励下纵摇,垂荡与横摇运动的时间历程曲线。图中实线为船舶与液舱耦合运动时历曲线,虚线则为LNG船模在相同吃水下不计液舱影响的运动时历曲线。两种运动时历曲线均在OpenFOAM下求得。
图7、8分别为迎浪工况下载液LNG船垂荡与纵摇运动时历,试验中入射波周期为2.70 s,波幅为2.35 cm。图9、10分别为另一迎浪工况下载液LNG船垂荡与纵摇运动时历,其入射波周期为1.20 s,波幅为2.28 cm。从图7、8和图9、10都可以看出,在一高一低两个不同频率的入射波激励下液舱晃荡对船舶的纵向运动影响很小。
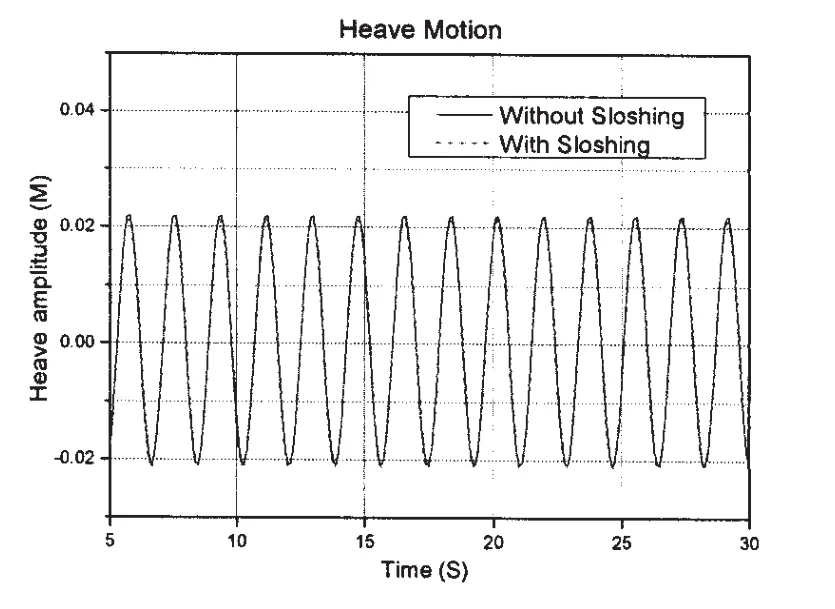
图11 横浪下垂荡运动时间历程(周期=1.80 s,波幅=2.27 cm)Fig.11 Time history of heave motion(Beam sea,T=1.80 s,ζa=2.27 cm)

图12 横浪下纵摇运动时间历程(周期=1.80 s,波幅=2.27 cm)Fig.12 Time history of pitch motion(Head sea,T=1.80 s,ζa=2.27 cm)
在横浪工况下,加载/不加载液舱的LNG船模横摇表现出了与上述迎浪工况的不同。图11、12分别为横浪工况下垂荡与横摇运动时历,此试验工况中,入射波周期为5.06 s,波幅为2.27 cm,入射波频率接近LNG船本身的横摇自振频率。从图11可以看出,在入射波频的作用下,加载/不加载液舱的LNG船模垂荡运动值十分接近,但图12中载液船模的横摇运动与不加载液舱的情况相比有着很大的不同。在波浪激励下相较于LNG船模的纵向运动,液舱晃荡激励的横摇力矩与船舶所受外部时域波浪横摇力矩量级相同。在不同频率的来波下,液舱晃荡激励的横摇力矩同波浪激励的横摇力矩之间存在的相位差也不同。图12所示的横摇工况中液舱晃荡激励的横摇力矩同波浪激励的横摇力矩的相位差在180°附近,两力矩耦合时相互抵消。因此加载液舱的船模横摇运动幅值要比不加载液舱的横摇运动幅值小得多,在一定程度上液舱流体晃荡有减少横摇的作用。

图13 横浪工况下数值与实验横摇RAOFig.13 Comparison of roll of experimental and numerical result(Beam sea)
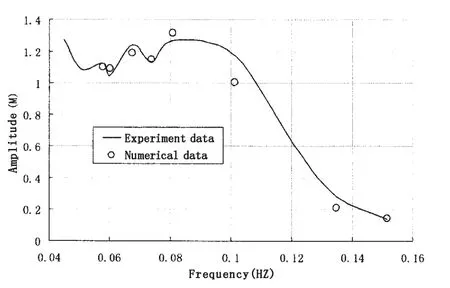
图14 横浪工况下数值与实验垂荡RAOFig.14 Comparison of heave of experimental and numerical result(Beam sea)
对不同频率入射波作用下载液船体耦合运动模拟计算和试验模拟的结果进行处理,可以得船体运动的幅值响应算子RAO。图13、14为船舶运动RAO的试验与数值计算结果的对比。图中曲线为耦合液舱晃荡的LNG船模在横浪工况下试验所得RAO曲线,散点为数值计算所得RAO幅值。从图13与14中可见,数值计算结果和试验结果在试验工况频率范围内吻合良好,表明本文采用的耦合液舱晃荡时域船舶运动数值计算方法是准确可行的。
5 结 论
本文将船舶在波浪上运动和液舱内液体晃荡问题分析采用不同的理论求解。时域船舶运动问题采用基于势流理论的脉冲响应函数方法求解,非定常液舱晃荡问题采用粘性流理论方法求解,并对时域内耦合液舱晃荡船舶的时域运动进行了数值计算模拟,并进行了相关试验研究。基于目前的研究结果,能够得出以下结论:
(1)液舱晃荡效应对载液船舶在波浪上的运动有着较为重要的影响,特别是对于横浪工况下的横摇运动。船舶运动的遭遇频率在船舶响应频率范围附近时,液舱晃荡诱导的横摇力矩同波浪诱导的横摇力矩之间的相位差在一定程度上减小了船舶横摇运动的幅值。可以预料,在较低频率的入射波激励下,液舱晃荡诱导的横摇力矩同波浪诱导的横摇力矩之间的相位差较小,两种横摇力矩的叠加会增大船舶的横摇运动幅值。在横摇共振频率附近,传统的基于势流理论的数值计算方法有一定的局限性,但仍然能够给出相对满意的结果。在横浪工况下,液舱晃荡对船舶的垂荡运动影响较小。在迎浪工况下,液舱晃荡所诱导的外力与外力矩对船舶的垂荡与纵摇等纵向运动的幅值影响均比较小。
(2)本文的数值计算结果表明开源CFD开发平台OpenFOAM为复杂粘性流场数值模拟提供了良好的开发和计算求解平台。OpenFOAM具有很好的底层结构框架,能够很好地适用于船舶与海洋工程水动力学领域的研究工作。OpenFOAM的开源特征,为广大研究者能够摆脱商业软件的束缚,开发出更多自主知识产权的优秀工程算法方法和计算软件提供了良好的基础平台。
(3)本文采用的数值计算模拟方法适用于计算分析载液船舶在波浪上的时域运动。特别是在需要长时间数值计算模拟情况时,在计算效率方面有着明显的优势。尽管本文计算和试验验证对象是载液LNG船,其比较结果是针对无航速船舶开展的,但方法本身同样适用于船舶的有航速时域运动。
[1]Kim Y.A numerical study on sloshing flows coupled with ship motion-the anti-rolling tank problem[J].Journal of Ship Research,2002,46(1):52-62.
[2]Faltinsen O M,Rognebakke O F.International Conference on Ship and Shipping Research[C].NAV,Venice,Italy,2000.
[3]Rognebakke O F,Faltinsen O M.Coupling of sloshing and ship motions[J].Journal of Ship Research,2003,47(3):208-221.
[4]Newman J N.Wave effects on vessels with internal tanks[C]//In:The 20th Workshop on Water Waves and Floating Bodies.Spitsbergen,2005.
[5]Lee C H,Newman J N.Computation of wave effects using the panel method[M].In:Numerical Models in Fluid-Structure Interaction.MIT press,Cambridge,MA,2005:211-251.
[6]Kim Y,Shin Y S,Lin W M,et al.Study on sloshing problem coupled with ship motion in waves[C]//In:The 8th International Conference on Numerical Ship Hydrodynamics.Busan,Korea,2003.
[7]Kim Y,Shin Y S,Lee K H.Numerical study on slosh-induced impact pressures on three-dimensional prismatic tanks[J].Applied Ocean Research,2004,26:213-226.
[8]Salvesen N,Tuck E O,Faltinsen O.Ship Motions and Sea Loads[J].Transactions,Society of Naval Architects and Marine Engineers,1970,78:255-287.
[9]刘应中,缪国平.船舶在波浪上的运动理论[M].上海:上海交通大学出版社,1986.
[10]戴遗山.舰船在波浪中运动的频域与时域势流理论[M].北京:国防工业出版社,1998.
Simulation of ship motions coupled with tank sloshing in time domain based on OpenFOAM
LI Yu-long1,ZHU Ren-chuan1,MIAO Guo-ping1,FAN Ju1,LU Zhi-mei2
(1 The State Key Laboratory of Ocean Engineering,School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;2 Marine Design and Research Institute of China,Shanghai 200011,China)
Tank sloshing in ship cargo is excited by ship motions,in the meantime the sloshing flow induces impact load on tank wall,then affects the ship motion.Wave forces acting on ship hull and the retardation function are solved by using strip method and an impulse response function method based on the potential flow theory,and global ship motion is established coupling with nonlinear tank sloshing which is simulated by viscous flow theory.Based on the open source CFD development platform OpenFOAM,numerical calculation of ship motion coupled with tank sloshing is achieved and the corresponding numerical simulation and validation are carried out.Through this method,the interactions of wave,ship body and tank sloshing are completely taken into considerations.This method has quite high efficiency for it takes advantage of potential flow theory for outer flow field and viscous flow theory for inside tank sloshing respectively.Numerical simulation and experimental studies indicate that the numerical results of ship motion coupled with tank sloshing can clearly show the coupling effect of tank sloshing on the ship global motion.The results of the ship motion of both computational and experiment ones agree well each other.
OpenFOAM;tank sloshing;impulse-response function;coupling motion;time domain simulation
U661.3
A
1007-7294(2012)07-0750-09
2011-09-15 修改日期:2012-03-19
李裕龙(1985-),男,上海交通大学船舶海洋与建筑工程学院博士研究生,研究方向:船舶与
海洋工程水动力学;朱仁传(1969-),男,教授,博士生导师,E-mail:renchuan@sjtu.edu.cn。
