两个气泡相互作用的某些动力特性研究

李章锐 ， 宗 智 ，b， 董 婧 ， 孙 雷 ，b

（大连理工大学a.船舶工程学院；b.工业装备结构分析国家重点实验室，辽宁 大连 116023）

两个气泡相互作用的某些动力特性研究

李章锐a， 宗 智a，b， 董 婧a， 孙 雷a，b

（大连理工大学a.船舶工程学院；b.工业装备结构分析国家重点实验室，辽宁 大连 116023）

文章采用边界积分方法模拟三维水下气泡的动力特性，详细阐述气泡计算的数学模型和数值实施过程，探究了三种不同浮力参数情况下（无重力、弱浮力、强浮力）气泡的演变情况。计算结果表明，在不同的浮力参数下，气泡形状和射流特点有着显著的区别，射流形成和发展与重力有着密切的联系。文中计算了两气泡在不同距离和不同强度参数下的相互作用的特点，为气泡动力特性的研究提供了参考。

边界积分法；气泡动力特性；浮力参数；射流

1 引 言

气泡为我们日常生活所熟知，并在物理、化学、医学和技术等领域占据着重要地位，然而它的行为特点有时很令人吃惊和难以预测，而且在很多情况下不为人们所知。由于气泡在流体系统的众多领域存在，因此气泡在当今的科学和技术领域占据着十分重要的地位。举几个简单例子：在石油的生产和传输过程中，人为地注入气泡可以把重油从地底输送到地表；在能源生产中通过沸腾使水变成蒸汽从而推动涡轮转动的整个过程中，气泡起着十分重要的作用；化工领域，液气反应堆里依靠气泡来增加不同相之间的接触面积；在喷墨打印中，泡沫室产生的气泡可以用来标记电离子的运动轨迹。

最早研究气泡溃灭的研究可以追溯到Rayleigh（1917）[1]，他应用能量方程计算了球形空化气泡在无粘无旋流体中压力情况。后来Kornfeld和Suvarov等人（1944）[2]提出射流的形成可能是空化损伤的一个原因。Benjamin和Ellis（1966）[3]为气泡射流的机理做了进一步的研究，他们用气泡冲量的概念来解释气泡溃灭，射流形成，以及环形气泡形成等现象。他们的实验为气泡由于重力作用或受到附近固壁效应的作用而形成射流提供了很好的验证。Blake和Gibson（1981）[4]提出了利用近似积分方程来模拟近自由液面附近空化气泡的生长和溃灭过程，观察到了气泡溃灭时射流的加速形成过程和自由液面的明显水冢现象。Wilkerson（1990）[5]利用边界积分方法计算了水下爆炸气泡在刚性固壁附近的溃灭情况。近年来Wang，Zhang等人[8-9]进一步在Wilkerson等人的基础上，采用边界积分法（Boundary Integral Method,BIM）模拟了结构物附近三维非对称水下爆炸气泡的运动情况，他们提出的光顺计算[6]和弹性网格技术[7]使得三维气泡运动模拟过程变得更加稳定可靠。在国内，张阿漫等人[16]基于势流理论用高阶边界元法对气泡的运动特性进行了研究，得到了一些有价值的结论。当前对单个气泡特性的研究相对较多，但对于多个气泡研究还不够深入。本文在前人的研究成果的基础上，数值模拟两个气泡在不同浮力和距离、强度情况下，两个气泡的相互作用情况，试图揭示水下气泡的某些动态特性。

2 计算模型

假设流体是无粘、不可压缩的，并且引起的运动是无旋的，因此在流体域内存在势函数φ x,y,（）z，满足Laplace方程：

采用Green第二定理，控制方程Laplace方程的边界积分方程的表达形式为：

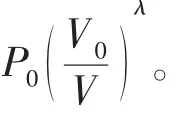
其中，V0，P0为初始不可凝结气体体积和压强，λ为热比率。对蒸汽气泡λ=1.4，对TNT炸药产生的气泡，λ=1.25。

为便于计算，所有的变量采用无因次的表达形式。无量纲参数参见表1所示。

图1 计算坐标系示意图Fig.1 Schematic plan of coordinate system for calculation

表1 无量纲参数Tab.1 Dimensionless parameters

上表中Rm代表Rayleigh[1]气泡半径，相当于在一个无限流场，不考虑重力情况下，球对称气泡的最大半径，d为空间中两物体相距的实际距离。ΔP=P∞-Pc定义为压强标尺，即与气泡等深无穷远处流体静水压力P∞与气泡内的饱和蒸汽压力Pc的压力差，ρ为流体密度，g为重力加速度，P0为气泡内的初始压强。

流体域内对应该控制方程的边界条件为：

运动学条件：

无穷远边界条件：

动力学条件：非定常伯努利方程满足动力学边界条件：

结合气体状态方程，气泡运动的动力学边界条件可改写为：

结合无量纲参数表1，以上动力学边界条件可以化简为：

气泡刚开始，假定在t=0时刻为初速度为0、半径为R0的高压气团，在整个流域内，初始时刻φ=0在气泡初期运动中，体积很小，浮力相对影响微弱，气泡的初始状态可以采用Rayleigh-Plesset[15]（无因次形式）方程描述：

依据该方程可以推导出[10]

其中R为气泡的无量纲半径，当给定ε和λ，方程（10）采用非线性方程的牛顿迭代法可以求解出气泡的初始半径 R0。 这样以上方程（2）、（4）、（8）和（10）构成了气泡运动求解的完整方程。

3 数值方法

对气泡的数值模拟，本文对其进行三维边界单元模拟，采用三角单元模拟球形气泡表面。气泡表面的初始离散是基于20面体来完成的。20面体形状由20个等边三角形和位于球形边界上的12个节点组成。这种划分可以通过不断地把原来的等边三角形细分成更小等边三角形来实现球形表面的逼近。每个三角形被细分的次数称为级，1级精度三角单元即为二十面体，2级精度的三角形单元有42个节点和80个三角形单元（如图2所示）。随着划分级别的不断提高，原始二十面体的形状的粗糙度降低，整个多面体的表面逐渐逼近于球面。对于n级精度来说，球面三角形由10n2+2个节点和20n2个单元构成。通常情况下气泡求解采用6级以上精度能准确描述气泡的运动状态。

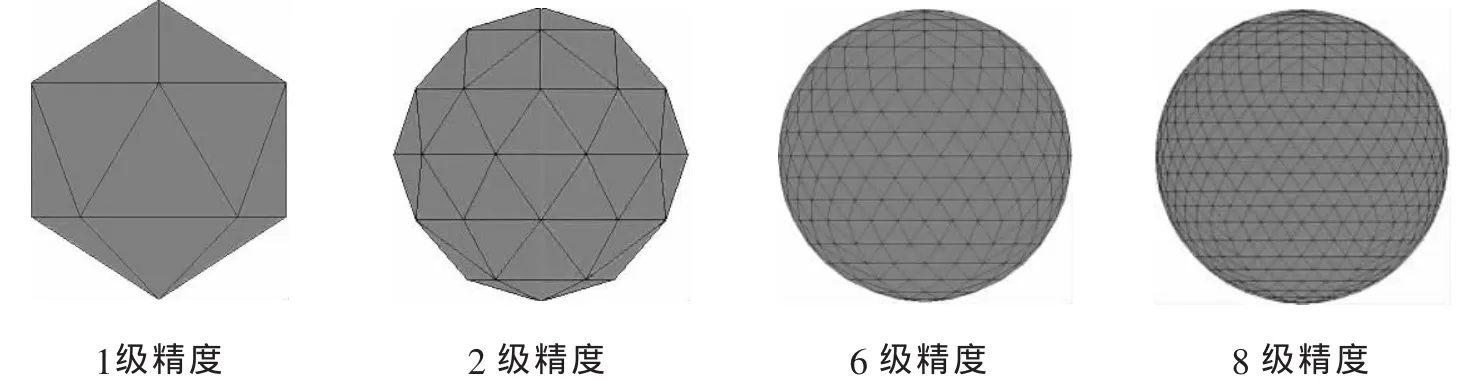
图2 不同离散级别的初始气泡表面示意图Fig.2 Schematic plan of discretized initial bubble surface with different levels

3.1 离散气泡边界的积分计算

（1）气泡边界参数的表达

当完成气泡表面单元划分后，边界积分方程（2）可以表示成为所有边界单元上的积分求和。因此需要引入以正交斜坐标系统来表示气泡表面上一任意的三角单元ABC将气泡表面离散化，如图3（a）所示，气泡每一个单元的计算，采用线性单元局部坐标系（ξ,η ），把任意的三角形单元ABC映射到ξη平面内的正三角形上。如图3（b）所示，分别把BC和AC映射到坐标轴η和ξ上，则气泡的任意一个三角形单元的三个顶点A、B和C分别落在（1,0）、（0,1）和（0,0 ）上，则线性插值表示的几何位置函数 r，速度势 φ 和法向速度 ψ=∂φ/∂n 如下：

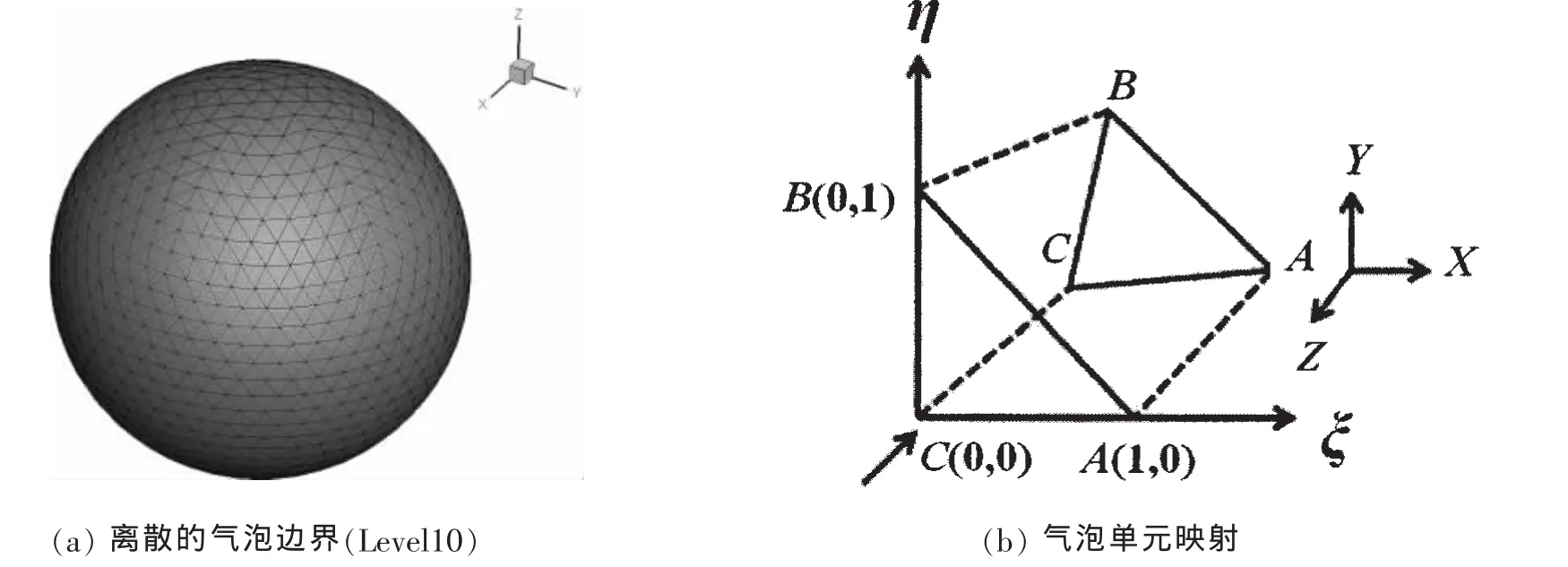
图3 离散的气泡边界及单元映射Fig.3 The discrete bubble surface and the element coordinate mapping

将（11）、（12）式和（13）式代入方程（2）右端项，则第一部分在三角形ABC上的积分表达为：

其余部分表达为：

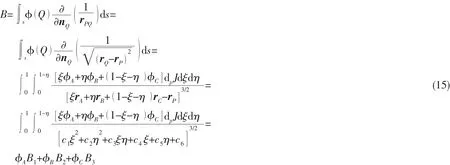
即Ai（i=1,3）和Bi（i=1,3 ）为影响系数；n是三角形ABC的外法向单位向量；（14）式和（15）式中各参数由（16）式至（29）式给出。

系数矩阵A和B为影响系数是整个求解的关键，也是耗费计算机CPU运算的主要部分。系数矩阵A和B的非对角元素采用7点高斯积分进行计算。而对于系数矩阵A和B矩阵的对角元素的积分存在奇异性。由于A矩阵对角元素是弱奇异，通过将直角坐标系求解转化到极坐标条件下求解即可以消除积分的奇异性[11]。B矩阵的对角元素具有强奇异，可采用4π法则求解,详细推导可参见Klaseboer文献 [12]，即：

当边界的初始位置和边界上初始速度势（对于气泡表面，初始时刻的速度势φ=0）给定后，通过求解Laplace方程（2）可以得到速度势法向速度∂φ/∂n，然后通过有限差分法[6]求解得到气泡的切向速度，当边界上的▽φ求得后，利用公式（4）和（8）可以得到下一时刻的气泡节点的位置和速度势，求解过程由于会产生数值不稳定，需采用光顺技术[6]和EMT[7]技术。

4 计算模型验证

4.1 与普通非爆炸气泡的对比

Lawson[13]曾采用质点影像测速技术（简称PIV技术）在实验中模拟过水下普通气泡破裂过程。他们在尺寸为600×600×800（mm）水箱中给一橡胶气球充气至300 cm3的大小，以模拟真实气泡，然后用一长钉刺穿气球，使之产生初始运动，再由PIV设备记录气泡在水下运动各时刻的情况。为模拟真实情况，本文数值计算中参数依照实验设置如下，如表2所示。

表2 气泡初始参数设置Tab.2 Parameters of initial bubble

图4 50，60，70，80ms时刻计算得到气泡形状与试验对比（虚线代表实验数据，实线代表数值计算）Fig.4 The calculated bubble shapes compared with those of experiment at 50,60,70,80 ms

数值计算采用6级精度，初始气泡表面离散为362个节点和720个三角单元。气泡运动的实验与仿真结果如图4所示。图中依次给出了50 ms、60 ms、70 ms和80 ms时刻的气泡运动剖面图。实线代表数值仿真的结果，虚线代表实验测得的结果，从图中可以看到，仿真过程中考虑了重力的影响，与实验条件一致。整个过程中气泡都在竖直向上运动，初始时刻运动较为缓慢，随着时间的增长，开始加速运动，由球形变为非球形，在t=50 ms时，气泡底部出现明显凹陷，在t=60 ms和70 ms时刻，气泡继续上浮，其底部的凹陷进一步加深，逐渐形成向上的射流，在t=80 ms时刻，射流即将冲破气泡对面的壁面，在实验中气泡在90 ms被射流冲破，而数值仿真中是92 ms，结果十分接近真实值。整个数值模拟与实验基本吻合，说明边界积分方法能够较为真实地模拟出气泡运动情况。数值仿真中我们也发现数值模拟与实际观察仍然存在一些差别，实验中橡胶气球中气体有5%到10%的压缩而实际仿真中暂没有考虑。此外，数值仿真中存在着截断误差和累计误差（在下个实验对比中可以看到），这些都是误差产生的重要原因，但整体说来，边界积分法能够较为准确地模拟出气泡运动的真实状况。

4.2 与Rayleigh 气泡半径的对比

在不考虑重力影响的情况下，在无限流域（忽略自由液面和固壁效应）中的一个振动气泡的运动状况可以用Rayleigh-Plesset方程描述，如（9）式所示。该方程可以通过相应数值算法，如四阶Runge-Kutta或五阶Runge-Kutta-Felhberg[14]（RKF），本文采用五阶RKF求解。在BIM数值仿真中气泡采用7级精度，初始气泡表面离散为492个节点和980个三角单元，如图5所示。求解参数如下。

表3 Rayleigh气泡初始参数设置Tab.3 Initial parameters for Rayleigh bubble

从计算结果看，实线代表采用RKF求解得到的气泡运动半径，星号代表的是用边界积分法（BIM）数值仿真得到的气泡半径，绿色（Err）虚线代表两者的误差，可以看到两者吻合良好，说明边界积分法能够很好地模拟无限流场的气泡运动状况，从误差比较可以看到，在气泡膨胀期间两者的误差较小，在气泡收缩时两者误差较大，而且随着求解周期的增加，从图中可以看到，到第三个周期，误差增长已十分迅速。采用BIM计算得到的结果误差会逐渐增大。但通常情况下数值仿真求解气泡周期为1-2个（第二个周期后的气泡运动状态有待进一步探究），因此不会对求解结果造成太大误差。

图5 采用RKF方法和BIM方法求得瑞利气泡半径随时间的变化Fig.5 The radius variation and error accumulation of Rayleigh bubble obtained by RKF and BIM

5 两个气泡的某些特性研究

5.1 浮力参数对气泡运动特性的影响

当浮力参数δ比较小的时候，气泡所受的浮力的影响可以忽略不计，这种近似适用于大压力（深水情况下）的体积较小的气泡。为此我们计算了在不同浮力参数下（δ为零，δ较小，δ较大情况下）气泡的运动特点。这里浮力参数分别选取δ2=0，δ2=0.05和δ2=0.25计算条件，计算气泡的运动及其射流情况，以下参数均为无因次参数。

（a） 无重力（δ2=0）

首先考虑100 m水深下的两气泡，由于水深较深，自由液面的影响可以忽略，初始半径均为0.139 1，最大半径为1，气泡中心相距2，强度参数ε=120，浮力参数为δ=0（即零重力），气泡精度为12级（即1 442个节点，2 880个单元 ），光顺技术每10实施一次，并采用EMT技术更新气泡位置和速度势，图6给出了几个典型时刻气泡的计算结果图。

初始时刻两气泡为一高温高压球体，由于气泡内部压力远远高于外界水压力，气泡开始膨胀，在t=0.210 6时刻看到气泡体积明显增长，但依旧保持球形，在t=1.133 4时刻，气泡体积达到最大，在两气泡相邻的部分气泡已不再保持球形，微微呈现出扁平形状，说明气泡间发生了相互排斥。随后气泡体积开始缩小，在t=1.917 8时刻，中部出现明显的扁平，排斥作用进一步加强，在t=2.184 0时刻两气泡外侧出现水平凹陷，开始形成水平射流，在t=2.253 8时刻，气泡体积继续缩小，射流方向依旧保持水平并进一步发展，即将要冲向气泡的对面壁面。

（b） 弱浮力（δ2=0.05）

在弱浮力即δ2=0.05条件下，在初始时刻及膨胀的初期（t=0.089 7时刻）气泡保持球形，在t=1.270 7时刻气泡体积达到最大，但中部仍然出现扁平，两气泡发生排斥作用。随后气泡体积开始减小，在t=1.941 7时刻，气泡已不再保持球形，远离两气泡的部分的下侧出现凹陷，在t=2.194 1时刻远离两气泡的部分的下侧出现斜向上的射流，在t=2.237 4斜向上的射流进一步发展，冲向气泡壁面。射流发展的方向是重力和两气泡之间的吸引力共同作用的结果，但由于重力作用较小，宽度较窄，规模较小，如图7所示。

图6 无重力状态下两气泡的演化过程Fig.6 The evolution of two bubbles without gravity

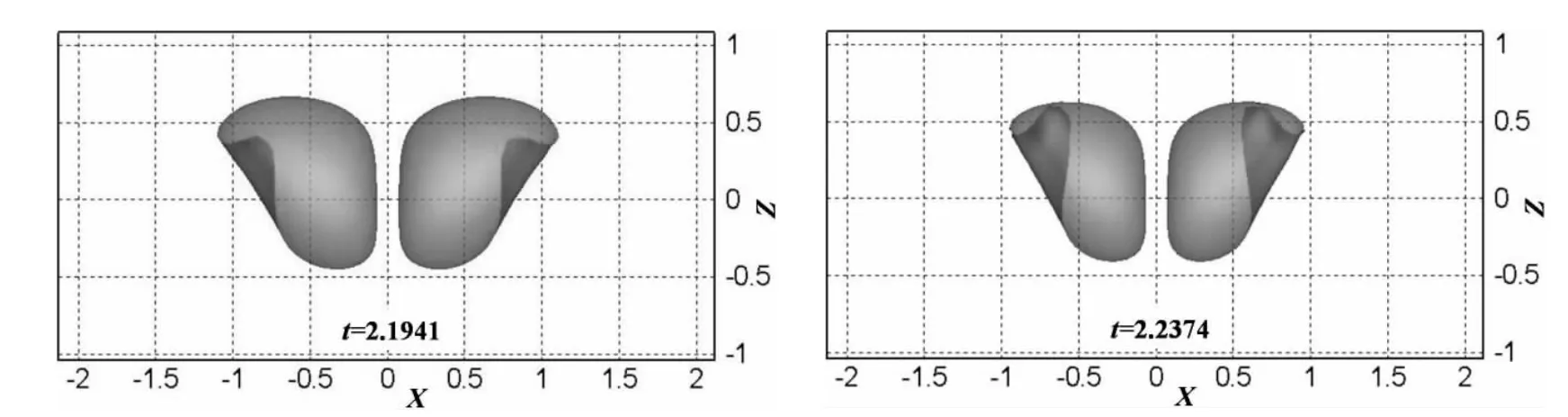
图7 弱浮力状态下两气泡的演化过程Fig.7 The evolution of two bubbles with weak buoyancy effect

（c） 强浮力（δ2=0.25）

在强浮力即δ2=0.25条件下，气泡在膨胀期间与无浮力和弱浮力条件类似，依旧是球形膨胀，如t=0.202 4时刻所示。在t=1.073 9时刻，气泡继续膨胀，接近气泡的最大体积，当两气泡距离足够近时气泡相邻部分出现排斥。在t=1.6434时刻气泡底部出现明显凹陷，在t=1.954 2时刻气泡底部出现斜向上射流，与弱浮力条件相比，射流的宽度明显增加，规模增大。在t=2.227 9时刻，射流冲向对面的气泡壁面。与弱浮力条件下相比，强浮力状况下射流形成的时间明显提前，如图8所示。

图8 强浮力状态下两气泡的演化过程Fig.8 The evolution of two bubbles with strong buoyancy effect

（d） 参数分析

图9给出了不同浮力参数下两气泡中心横向位置的变化，从图中可以看到无论在无重力还是弱浮力或强浮力状况下，两气泡的距离都是先增大后减小，也就是在膨胀期间，两气泡间发生排斥，气泡之间距离增大，在气泡溃灭期间两气泡发生吸引，气泡之间距离减小。图10给出了不同浮力参数下气泡中心垂向位置的变化，可以看到随着浮力参数的增加，气泡上升的速度加快。图11给出了不同浮力参数下体积随时间的变化。气泡在膨胀过程中体积增长基本一致，但溃灭时随着浮力参数增加，气泡体积收缩的速度有所减慢。图12给出了气泡在不同浮力下动能（Kinetic）、势能（Potential）和总能量（Total）随时间的变化，在气泡膨胀时，气泡的动能逐渐降低而势能逐渐升高，而气泡溃灭时，气泡的动能逐渐升高而势能逐渐降低，气泡的总能量在整个气泡运动过程中是守恒的。

图9 气泡中心横向距离的变化Fig.9 The variation of transverse distance of two bubbles

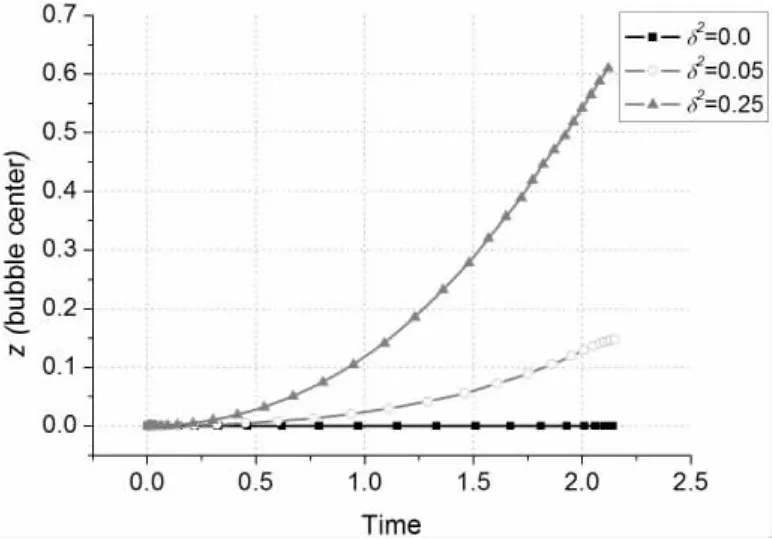
图10 气泡中心垂向位置的变化Fig.10 The variation of vertical position of bubble

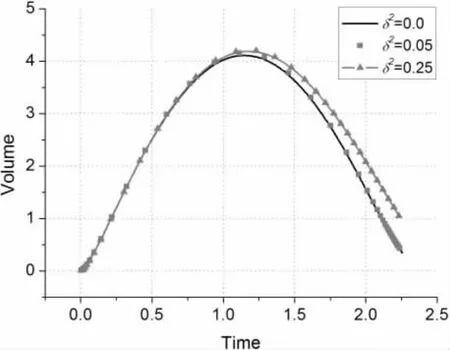
图11 气泡体积随时间的变化Fig.11 The bubble volumes as a function of time

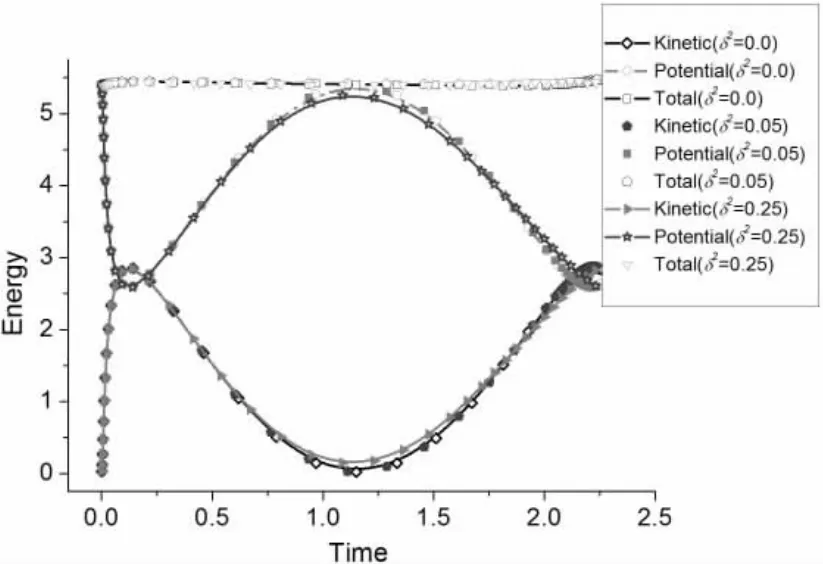
图12 气泡能量随时间的变化Fig.12 The bubble energy as a function of time

图13给出了不同浮力参数下射流点速度的变化，可以看到初始阶段气泡射流点速度随浮力参数的增大而增大，对于无重力或弱浮力 （δ2= 0,0.05 ）情况，随着时间的增长，气泡射流点速度逐步增大，会达到一个较高峰值。对于浮力参数较大 （δ2=0.25,0.3,0.4）时射流点速度却经历了先增大后减小的过程，射流点速度最大峰值相对于无重力或弱浮力情况小，也就是说，浮力较小的情况下，射流的宽度较窄，速度可能很大，浮力较大时，射流的宽度较大，但速度峰值却要小一些。

5.2 横向距离参数和强度参数对气泡运动特性的影响

（a）不同横向距离下的比较

为进一步考察气泡横向距离对气泡运动特性的影响。在无重力情况下，我们计算了气泡中心横向（x方向

）距离为两倍、三倍、五倍和七倍最大半径情况下气泡的运动情况，计算的其他参数和5.1节（δ2=0）中相同。计算结果表明两气泡在不同横向距离的演化形态与两倍条件下类似。不同的是，从图14可以看到随着两气泡距离的增大，两气泡中心变化的幅值越来越小，也就是说气泡间作用排斥和吸引越来越小，在五倍以上的最大半径距离时，气泡的作用已比较微弱了。图15给出了不同距离下气泡体积随时间的变化，随着距离的增大气泡的收缩速率加快，距离越大，气泡射流点后期体积越小。气泡体积变化率（体积对时间求导）如图16所示，从图中可以看到气泡膨胀初期和溃灭末期气泡变化速率都较为剧烈。图17给出了不同距离下气泡射流点速度随时间的变化，射流点初期在不同距离下无明显差别，后期的速度随距离的增大而增大。

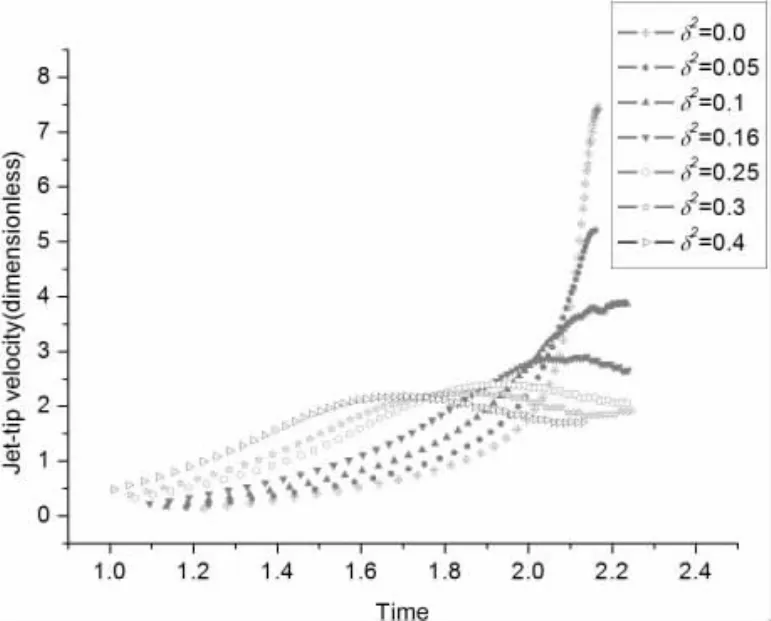
图13 不同浮力参数下射流点速度的变化Fig.13 The jet-tip velocity of bubble under different buoyancy parameters

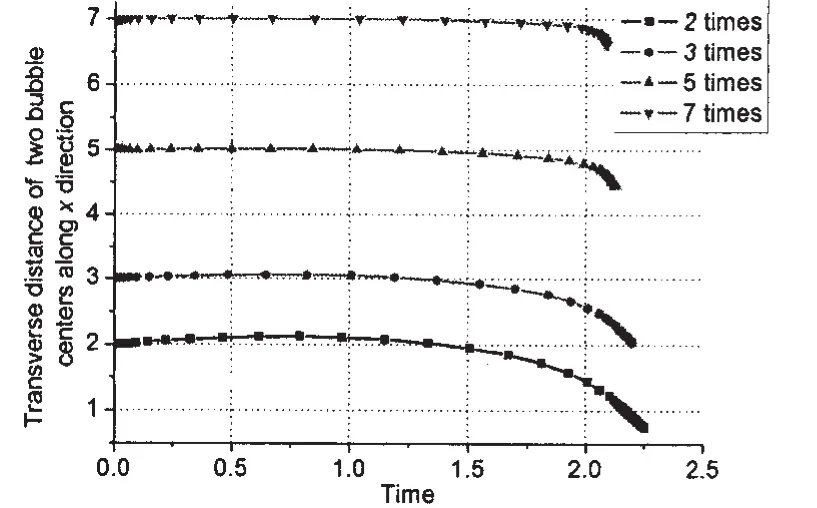
图14 气泡中心横向距离的变化Fig.14 The variation of transverse distance of two bubbles

图15 气泡体积随时间的变化Fig.15 The bubble volumes as a function of time

图16 气泡体积变化率随时间的变化Fig.16 The bubble volume change rate as a function of time

图17 不同距离下射流点速度的变化Fig.17 The maximum velocity of bubble under different distances

（b）不同强度参数下的比较

为进一步考察气泡强度参数对气泡运动特性的影响，在无重力情况下，我们计算不同强度ε=20，60，120，180参数情况下气泡的运动情况，计算的其他参数和5.1节（δ2=0）中相同。气泡演化的形态与ε=120的类似。从图18可以看到，气泡运动过程中，两气泡中心横向距离都有先缓慢增大后迅速减小的规律，但随着两气泡强度参数的增大，两气泡中心横向距离变化的幅值增加，也就是说气泡间排斥和吸引作用增强。图19给出了不同强度参数下气泡体积随时间的变化，气泡强度增大，气泡的运动周期明显增大，气泡膨胀到最大体积的时间会越晚，图20给出气泡体积变化率随时间的变化，气泡在膨胀初期和溃灭末期的运动都十分剧烈。图21给出了不同强度参数下气泡射流点速度随时间的变化，射流点在初期速度变化较为平缓，在末期射流速度急剧增加；随着强度参数增加，射流发生穿透的时间越晚。

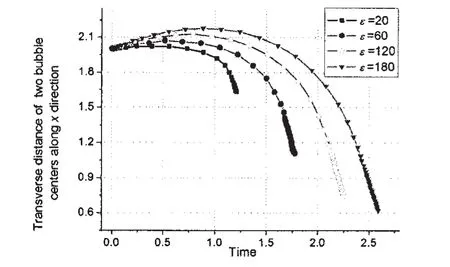
图18 气泡中心横向距离的变化Fig.18 The variation of transverse distance of two bubbles

图19 气泡体积随时间的变化Fig.19 The bubble volumes as a function of time

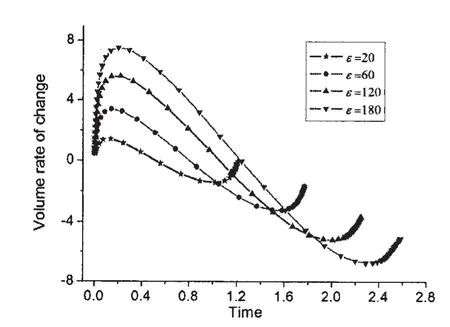
图20 气泡体积变化率随时间的变化Fig.20 The bubble volume change rate as a function of time

图21 不同强度参数下射流点速度的变化Fig.21 The maximum velocity of bubble under different strength parameters

6 结论与讨论

本论文中采用三维边界积分模拟水下两个气泡相互作用的问题，详细论述了采用边界积分法求解气泡运动的算法和数值实施过程，并总结出以下结论：

（1）边界积分法（BIM）能够较好地模拟实际气泡的运动状况，无论是非爆炸气泡还是爆炸气泡都能准确地描述和模拟出气泡的运动状态和各个时刻气泡特征参数变化。

（2）无论是无重力、弱浮力还是强浮力条件下，气泡两者之间主要表现为膨胀时相互排斥，溃灭时相互吸引。与无重力和弱浮力比较，强浮力作用下射流的出现时间明显提前，并且射流的宽度和规模都更大，也就是说，重力对射流形成和发展有着重要的影响。无重力和弱浮力条件下，射流速度随时间逐步增加并在末期急剧上升，强浮力作用下，射流速度经历了由大变小的过程，强浮力条件下的射流速度峰值小于无重力和弱浮力条件下的。

（3）气泡在膨胀初期和溃灭末期的变化都十分剧烈，两气泡的作用随着距离参数的减小和强度参数的增大越来越明显，在五倍以上的距离参数条件下，两气泡的作用已比较微弱了。无重力条件下，在不同距离下射流点速度在初期无明显差别，后期的速度随距离的增大而增大；不同强度参数下，气泡射流点在初期速度变化较为平缓，在末期射流速度急剧增加；随着强度参数增加，射流发生穿透的时间越晚。

[1]Rayleigh L.On the pressure developed in a liquid during the collapse of a spherical cavity[J].Phil.Mag.,1917,34:94-98.

[2]Kornfeld M,Suvarov L.On the destructive action of cavitation[J].Journal of Applied Physics,1944,15:495-506.

[3]Benjamin T B,Eillis A T.The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries[J].Phil.Trans.Roy.Soc.,London,Ser.A,1966,260:221-240.

[4]Blake J R,Gibson D C.Growth and collapse of a vapour cavity near a free surface[J].J Fluid Mach.,1981,111:123-140.

[5]Wilkerson S A.A boundary integral approach to three-dimensional underwater explosion bubble dynamics[D].PHD.Thesis.The Johns Hopkins University,1990.

[6]Zhang Y L,Yeo K S,Khoo B C,Wang C.3D jet impact and toroidal bubbles[J].Journal of Computational Physics,2001,166:336-360.

[7]Wang C,Khoo B C,Yeo K S.Elastic mesh technique for 3D BIM simulation with an application to underwater explosion bubble dynamics[J].Computers and Fluids,2003,32:1195-1212.

[8]Wang Q X.The evolution of gas bubble near an inclined wall[J].Theoretical and Computational Fluid Dynamics,1998,12:29-51.

[9]Zhang Y L,Yeo K S,Khoo B C,Chong W K.Three-dimensional bubbles near a free surface[J].Comput.Phy.,1998,146:105-123.

[10]Klaseboer E,Khoo B C.A modified Rayleigh Plesset model for a non-spherically symmetric oscillating bubble with applications to boundary integral methods[J].Eng.Anal.Bound.Elem.,2006,30:59-71.

[11]Wilkerson S A.Boundary integral technique for explosion bubble collapse analysis[C]//Proc.ASME Energy-Source Technology Conference and Exhibition.Houston,Texas,1989.

[12]Klaseboer E,Fernandez C R,Khoo B C.A note on true desingularisation of boundary integral methods for three-dimensional potential problems[J].Engineering Analysis with Boundary Elements,2009,33,6:796-801.

[13]Lawson N J,Rudman M,Guerra A,Liow J L.Experimental and numerical comparisons of a large bubble[J].Experiments in Fluids,1999,26:524-534.

[14]Alehossein H,Qin Zongyi.Numerical analysis of Rayleigh-Plesset equation for cavitating water jets[J].Int.J Numer.Meth.Engng.,2007,72:780-807.

[15]Best J P,Kucera A.A numerical investigation of non-spherical rebounding bubbles[J].Fluid Mech,1992,245:137-154.

[16]Zhang A M,Yao X L,Yu X B.The dynamics of three-dimensional underwater explosion bubble[J].Journal of Sound and Vibration,2008,311(3-5):1196-1212.

Some dynamic characteristics of the interactions of two bubbles

LI Zhang-ruia,ZONG Zhia,b,DONG Jinga,SUN Leia,b

(a.School of Naval Architecture;b.State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology,Dalian 116023,China)

Dynamic characteristics of three-dimensional underwater bubbles are simulated using boundary integral method.The mathematical model and numerical implementation are presented in detail.The evolution of the two bubbles under three different buoyancy parameters(no gravity,weak buoyancy parameter and strong buoyancy parameter)was investigated.The calculated results indicate that the bubble shapes and jet characteristics are very different under different buoyancy parameters.The jet formation and development have very close relationship with gravity effect.The interactions of two bubbles under different distances and strength parameters are also simulated.This study could provide a reference to the study of bubble dynamics.

boundary integral method;bubble dynamics;buoyancy parameter;jet formation

O351

A

1007-7294（2012）07-0717-13

2011-11-15 修改日期：2012-02-26

创新研究群体科学基金(50921001)；国家重点基础研究发展计划项目（2010CB83270）

李章锐（1985-），男，大连理工大学船舶工程学院博士研究生，E-mail:lizhangruix@yahoo.com.cn；宗 智（1964-），男，教授，博士生导师。