基于蚁群优化K-medoids的变电站特性聚类研究

刘建华 孟 颖 谭 智

（1.长沙理工大学电气与信息工程学院，长沙 410114；2.长沙理工大学计算机与通信工程学院，长沙 410114）

众多文献研究表明负荷特性对于电力系统运行，特别是电力系统的动态行为有很大的影响[1]，电力负荷模型准确与否直接影响到电力系统仿真结果的准确性[2-3]。建立精确的负荷模型用于电力系统的规划、设计、运行和研究越来越成为电力系统工程实际和学术研究的基本需要[4]。但是由于负荷自身的特殊性，建立精确的电力系统负荷模型非常困难。

随着对负荷建模研究的逐渐深入，负荷特性的分类与综合问题正在受到重视。电力系统负荷变化的规律性使负荷数据呈现出可分类的特点[5-6]。文献[7]中提出了基于改进K均值(K-Means)的负荷聚类算法对电网进行仿真分析。文献[8]中提出了模糊等价关系和模糊C均值(Fuzzy C Means，FCM)两种负荷聚类方法。文献[9]提出了基于自适应FCM聚类的电力负荷动特性分类方法。文献[10]提出了基于数据挖掘的多层次细节分解负荷聚类算法。

本文提出了一种蚁群优化 K-medoids综合算法（下文简称综合算法），并将其应用于变电站负荷特性聚类中，通过K-medoids算法对蚁群的历史最优位置进行聚类分析，将此位置代替K-medoids算法的参考点，作为新的聚类中心，数据可以自适应的加入到适合它的聚类当中。

1 基本原理

1.1 蚁群算法

蚁群算法是Colorni和Dorigo等人在90年代初期提出的一种新型智能模拟仿生优化算法[11]。蚁群算法由于具有正反馈、分布式计算以及贪婪启发式搜索等特点，成为人工智能领域的一个研究热点。目前对蚁群算法的研究已经渗入到多种不同的应用领域，如旅行商问题（TSP）、二次分配问题（QAP）、任务调度问题（JSP）等。

蚁群算法的基本原理是[12]，蚂蚁在运动过程中会释放一种信息素（pheromone）的物质，蚂蚁个体之间是通过该信息素进行运动方向的信息传递的，即蚂蚁不仅在所经过的路径上沉积了该种物质，而且蚂蚁在运动过程中能够感知这种信息素物质。因此，由大量蚂蚁组成的蚁群行为便表现出一种信息正反馈和相互协作的机理：某一路径上走过的蚂蚁越多，则后来者选择该路径的概率就越大，即运用群体信息素来作为引导它们运动轨迹方向的依据，最后蚂蚁能找到一条从蚁巢到食物源的最短路经，这就是整个群体得以完成复杂优化行为的实质问题。即使遇到障碍物情况，该基本原理仍然是不变的，只不过是在运动的途径上会增加沉积信息素的中间状态点来解决，信息交换构成一个正反馈过程仍是不变的。

1.2 K-medoids算法

K-medoids聚类算法[13]的基本策略是通过首先任意为每个聚类找到一个代表对象而首先确定n个数据对象的k个聚类；其他对象则根据它们与这些聚类代表的距离分别将它们归属到各相应聚类中。而如果替换一个聚类代表能够改善所获聚类质量的话，那么就可以用一个新对象替换旧聚类对象。这里将利用一个基于各对象与其聚类代表间距离的成本函数来对聚类质量进行评估。为了判定一个非代表对象Orandom是否是当前一个代表对象Oj的好的替代，对于每一个非中心点对象p，下面的4种情况被考虑。

第一种：p当前隶属于中心点对象Oj。如果Oj被Orandom所代替作为中心点，且p离一个Oj最近，i≠j，那么p被中心分配给Oi。

第二种：p当前隶属于中心点对象Oj。如果Oj被Orandom代替作为一个中心点，且p离Orandom最近，那么p被重新分配给Orandom。

第三种：p当前隶属于中心点Oi，i≠j。如果Oj被Orandom代替作为一个中心点，而p仍然离Oj最近，那么对象的隶属不发生变化。

第四种：p当前隶属于中心点Oi，i≠j。如果Oj被Orandom代替作为一个中心点，且p离Orandom最近，那么p被重新分配给Orandom。

每当重新归类时，平方误差E所产生的差别对成本函数有影响。因此，如果一个当前的中心点对象被非中心点对象所代替，成本函数计算平方-误差值所产生的差别。替换的总成本是所有非中心点对象所产生的成本之和。如果总成本是负的，那么实际的平方误差将会减小，Oj可以被Orandom替代。如果总成本是正的，则当前的中心点Oj被认为是可接受的，在本次迭代就无需变动。

2 蚁群优化K-medoids综合算法

2.1 基本思想

综合算法的基本思想：从蚁群中随机选取m个对象，计算任意两个对象之间的距离，确定蚁群间的距离和最初的聚类中心，并将此中心作为蚁群的历史最优位置，使用K-medoids算法对历史最优位置进行聚类分析，找到新的聚类中心，来代替蚁群算法逼近优化的中心点。首先，蚂蚁之间在利用蚂蚁释放的信息素，确定蚁群在可行解范围内的相对位置，实现蚂蚁之间的信息交换；其次，根据蚂蚁所在蚁群中心提供的信息素，扩大蚂蚁的搜索空间，从而避免蚂蚁陷入局部最优，加强算法对聚类所在空间区域的局部搜索能力；最后，从整个蚁群的角度出发，由于每只蚂蚁的搜索范围都集中于新的聚类所形成的区域，重新计算任意蚂蚁之间的距离，确定最终的聚类中心。

2.2 实现过程

1）流程图（如图1）

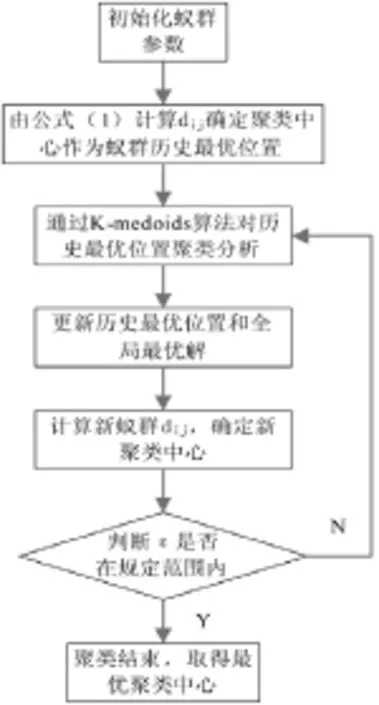
图1 综合算法流程图

2）实现步骤

设 X={Xi=(xi1，xi2，…，xim)，i=1，2，…，N}是待进行聚类分析的数据样本的集合。

Step1 对蚁群进行初始化操作，选择蚂蚁数目为m，NC-max为最大迭代次数，m个蚂蚁作为初始中心点，设初始中心点为（M1，M2，…，Mm）。

Step2 定义dij为Xi到Xj之间的加权欧氏距离

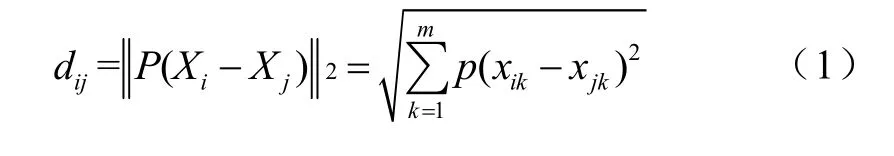
式中，P为权因子，可根据各分量在聚类中的贡献不同而设定。

设r为聚类半径，τ ij ( t)为t时刻数据样本Xi到样本Xj路径上残留的信息数量（Pheromone Quantity，PQ）PQ，设 τ ij ( 0)=0，即在初始时刻各路径上的PQ相等且为0。路径ij上PQ由式（2）给出

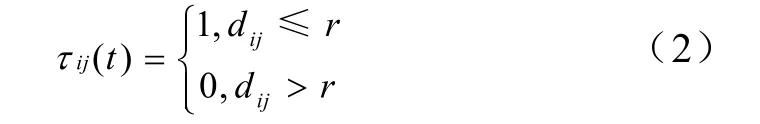
而Xi是否归并到Xj由式（3）给出

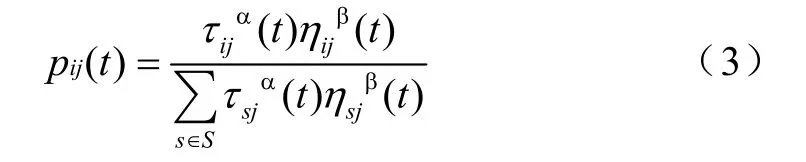
式中， p ij ( t)表示Xi归并到Xj的概率，若 p ij( t)≥p0，（0≤p0≤1），则Xi归并到Xj领域。其中，p0为一概率常数。S={Xs|dsj≤r，s=1，2，…，j，j+1，…，N}；η为局部的启发函数，表示由数据样本i转移到数据样本j的期望程度。α，β分别表示蚂蚁在运动过程中所积累的信息素及启发函数在样本转移路径的过程中所起的不同作用。

根据加权欧氏距离式（1），计算每只蚂蚁之间的距离dij，然后由式（3）计算 p ij( t)判断PQ，确定蚁群间的最优路径和聚类中心，并将此中心作为蚁群的历史最优位置。

Step3 根据K-medoids算法对蚁群的历史最优位置进行新的聚类分析。以ACO算法的历史最优位置作为K-medoids算法中的代表对象Oj，确定每只蚂蚁所在的聚类以及类与类之间的中心点。

Step4 对形成的新蚁群按照Step2的方法，计算每只蚂蚁代表的最优解，更新蚁群的历史最优位置和全局最优解。

Step5 重新计算任意蚂蚁之间的加权欧氏距离dij，确定新的聚类中心，找到最优路径。

Step6 定义Dj为第j个聚类的偏离误差，ε为聚类分析的总体误差。

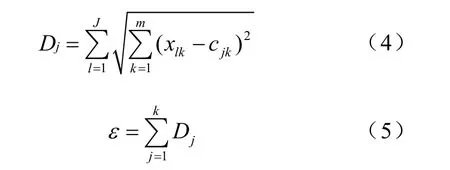
式中，cjk为第j个聚类中心的第k个分量。

判断ε是否在规定范围内，如在规定范围内，聚类终止，否则转向Step3继续迭代。

Step7 达到终止条件，聚类结束，取得最优聚类中心。

3 聚类实例

3.1 聚类数据

取文献[14]中福建省电力调度通信中心EMS提供的2005年夏季的典型电网变电站负荷构成数据进行聚类分析。矩阵U为变电站负荷构成参数，待分对象：U={u1，u2，u3，…，u44}为44个220kV变电站负荷构成参数；列对象参数：ui={uil，ui2，ui3，ui4}为各变电站的工业、农业、商业、城乡居民及其他4类典型行业负荷的构成比例。本文把变电站聚为4类。

3.2 聚类结果

如表1和表2所示，将综合算法与单一的FCM的聚类结果进行比较，以验证其聚类的效果。同时列出两种方法的聚类中心矩阵CFCM和C综合。

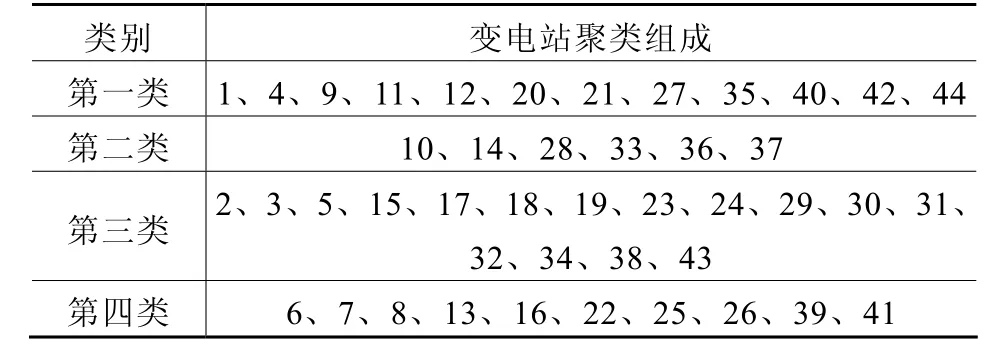
表1 FCM法的聚类结果

聚类中心矩阵为

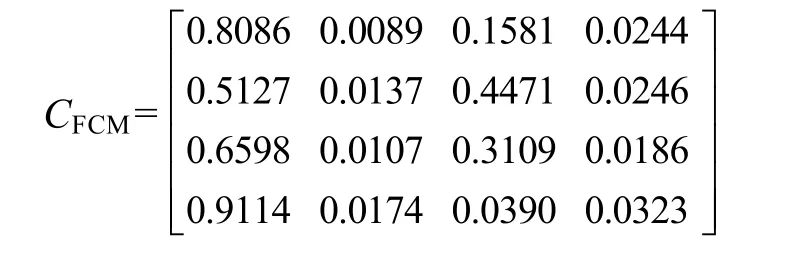
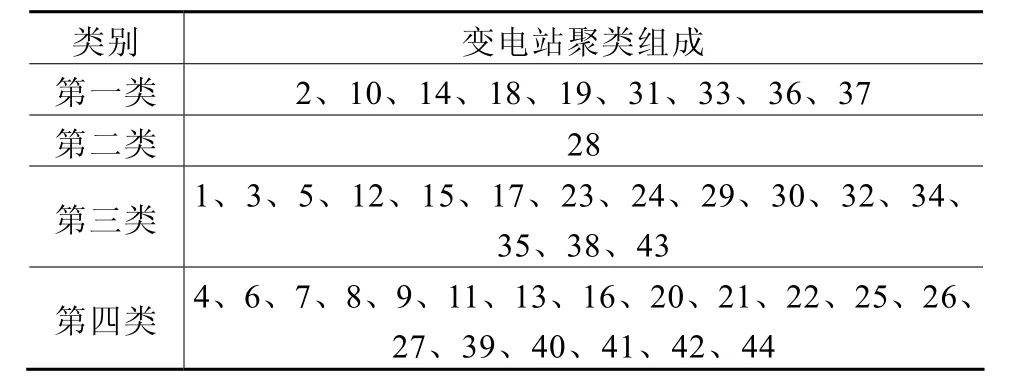
表2 综合算法的聚类结果

聚类中心矩阵为

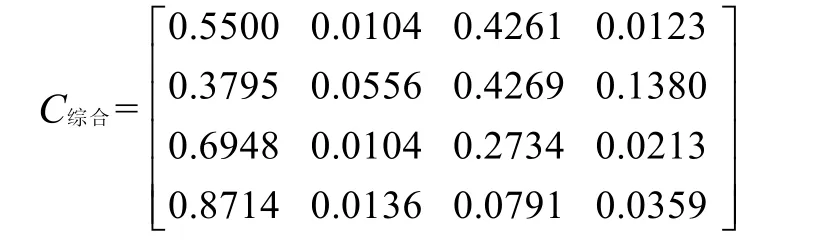
3.3 类间距离和类内距离比较

聚类结果的好坏要看是否有较高的类内相似性，较低的类间相似性。本文可以对它们的类间距离和类内距离进行比较，一般来讲，聚类中心的间距越大，样本与其所属中心的间距越小，聚类效果更好。因此，我们只列出它们的类间距离和类内距离进行比较。

1）类间距离：由聚类中心矩阵可以求得类间距离矩阵，取矩阵中的每个元素的平均值作比较，较大者则认为聚类效果比较好，反之亦然。如表3所示。

表3 类间平均距离比较

2）类内距离：类内平均距离比较如表4所示。

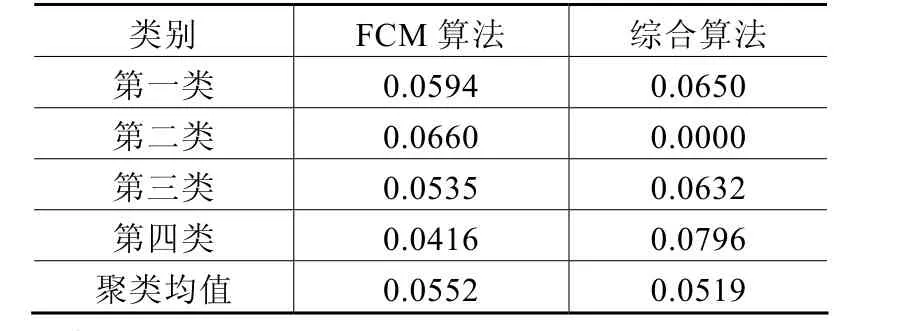
表4 类内平均距离比较

3.4 结果分析

1）如表3和表4所示，综合算法的类间距离有所变大，类内距离有所变小，可知综合算法在变电站的聚类中取得了较好的效果。

2）对聚类中心矩阵与变电站负荷构成数据进行比较，基于综合算法的聚类结果是有效和合理的。例如第一类，工业用电约占55%，商业用电约占43%，农业和城乡居民及其他各约占1%，基本上反映了第一类各变电站的综合静态负荷特性构成。聚类中心矩阵中可以较好地体现出每类变电站的综合静态负荷特性。

3）由聚类结果和中心矩阵可得出安装负荷测辨装置的变电站数量和具体位置，即负荷装置布测点的个数为聚类数，理想的安装测点是与聚类中心负荷构成特性最为接近的典型变电站。

4 结论

负荷特性分类与综合是实现负荷模型实用化的关键，为了建立合适的变电站负荷模型，本文将聚类方法引入到负荷特性分析，提出了基于蚁群优化K-medoids综合算法的电力负荷聚类。综合算法是PAM算法对蚁群的历史最优位置进行了聚类分析，ACO具有良好的正反馈性能、较强的鲁棒性、易于与其他算法结合等特点，使综合算法能更好地获得全局最优解，从而克服了PAM算法易陷入局部最优的缺点，并降低了对初始值的敏感度，提高了聚类的准确率。通过变电站特性聚类实例，将综合算法与FCM法聚类结果进行比较，证明了综合算法在电力系统负荷聚类的优越性。同时基于综合算法的负荷聚类为没有安装布测点的变电站建立实用模型提供了有效途径，因此，文中所得到的聚类结果和聚类中心矩阵为进一步开展负荷建模实用化工作提供了重要的参考依据。

[1]李娟,丁坚勇.电力系统负荷建模和算法的研究及进展[J].高电压技术,2008,34(10):2209-2215.

[2]李培强,李欣然,林舜江.电力负荷建模研究评述[J].电力系统及其自动化学报,2008,20(5):57-64.

[3]鞠平,谢会玲,陈谦.电力负荷建模的发展趋势[J].电力系统自动化,2007,31(2):1-4.

[4]贺仁睦.电力系统精确仿真与负荷模型实用化[J].电力系统自动化,2004, 28(16):4-7.

[5]章健,沈峰,贺仁睦.电力负荷模型结构的样条函数描述[J].电力自动化设备,2007,27(7):5-8.

[6]黄梅,贺仁睦,杨少兵.模糊聚类在负荷实测建模中的应用[J].电网技术,2006,30(14):49-52.

[7]白雪峰, 蒋国栋.基于改进 K-means聚类算法的负荷建模及应用[J].电力自动化设备,2010,30(7):80-83.

[8]李培强, 李欣然,陈辉华,等.基于模糊聚类的负电力负荷特性的分类与综合[J].中国电机工程学报,2005, 25(24):73-78.

[9]杨浩,张磊,何潜,等.基于自适应模糊C均值算法的电力负荷分类研究[J].电力系统保护与控制,2010,38(16): 111-115.

[10]张智晟,孙雅明,张世英,等.基于数据挖掘多层次细节分解的负荷序列聚类分析[J].电网技术,2006,30(2):51-56.

[11]周申培,严新平.遗传蚁群融合算法及在不确定性无功优化中的应用研究[J].电力系统保护与控制,2010,38(24):120-123.

[12]孙雅明,王晨力,张智晟,等.基于蚁群优化算法的电力系统负荷序列的聚类分析[J].中国电机工程学报,2005,25(18):40-45.

[13]朱明.数据挖掘[M].合肥:中国科技大学出版社,2008.11.

[14]鞠平, 陈谦, 熊传平,等.基于日负荷曲线的负荷分类和综合建模[J].电力系统自动化, 2006, 30(16):6-9.