线路故障过电压下变电站内空间电场的分析

栗 薇

（天津电力技术中心，天津 300384）

随着超高压输电在国内的普及，其线路和变电站周边的电磁环境，已经成为影响周边电力设备和其他设备正常运行的重要因素之一。

对于某些简单的输电线路模型有近似的解析公式来计算电场分布，而对于更加一般和复杂的情况，如电力系统中变电站开关场区和高压输电线路铁塔附近，必须采用计算机程序进行数值计算。常用的计算输电线路电场的数值方法有模拟电荷法、有限差分法、有限元法和蒙特卡洛法等。国内外对电力系统电磁环境的分析主要集中在分析线路在稳态情况下的工频电磁场[1-3]，其中文献[2]对架空线路的工频电场进行了分析计算，文献[3]对变电站内的空间工频电磁场进行了分析计算，目前，对线路和变电站内空间工频电场的计算方法已经非常成熟。

随着研究的深入，更多的文献开始关注可能引起二次设备误动的雷击、开关操作在线路上的波过程以及空间瞬态电磁场，文献[4]应用多导体传输线法分析了线路的瞬态波过程，文献[5-6]进一步应用矩量法并结合傅里叶变换分析了复杂结构架空导体在开关操作时的瞬态电磁场。但是前者对空间工频电磁场的分析模型较简单，不适合分析架构等复杂导体结构的影响，而后者计算方法复杂，耗时长。因此这两种高频计算方法，虽然可以分析开关操作等高频瞬态过程，但是对于线路故障过电压等较低频率的瞬态过程分析存在方法复杂、计算时间长的缺陷。

本文基于矩量法，提出了一种适合计算变电站内母线、设备间连线、架空线路产生的空间电场强度的方法。该方法以矩量法[7]和复电阻率[8]为基础，对复杂导体附近三维工频电场进行计算。可以考虑任意复杂布置的导线结构、模拟有弧垂的架空线，计算模型更接近电力系统的实际情况。它可以计算变电站内的导体结构、悬挂金具、跳线、弧垂、等各种可能对电场有影响的因素；并且计算模型可以考虑大地电阻率的影响，并且可以计算短路、雷击情况下的空间电场强度，使计算结果更接近实际情况，应用范围更加广泛。本文的方法使用导体表面上电位的连续性来建立方程组，即在导体段表面上两点间的电位差是由各导体段上的漏电流决定，而导体段内这两点间的电位差是由导体的自阻抗和流过导体段上的电流产生的，这两个电位差应当相等，同时导体段上的电流可以用各导体段上的电荷表示，从而建立了以各段导体的电荷量为待求变量的线性方程组，解之可得导体各段上的电荷分布。由这些电荷分布可以求得考虑各种架空导体产生的电场。该方法可以结合傅里叶变换可以分析在几百kHz以内的线路故障情况下变电站内线路的波过程及空间瞬态电磁场。

通过与其他文献计算结果的对比，验证了本文计算方法的正确性，最后，应用本文计算方法对某500kV变电站正常运行的工频电场和短路故障情况下空间瞬态电场分布进行了预测计算。

1 变电站内空间电磁场计算的基本方法

1.1 复电阻率的概念

无论是空气，还是土壤，都具有一定的电阻率和介电常数，在分析交流情况下铁塔周围的电场分布时，它们都会起作用。由安培环路定律

电流密度与电场强度之间的关系

有

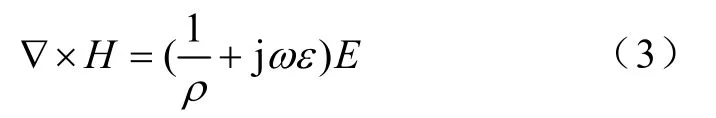
式中，H和 E分别为磁场强度和电场强度，ρ和 ε分别为介质的电阻率和电容率，ω为角频率。引入新的电流密度 J'，取从而得到介质的复电阻率

使用上面的复电阻率，在进行准静态场分析时可以将空气也视为一层漏电媒质，这样得到的格林函数就可以用来同时分析由接地部分以及输电线路产生的电场。对于多层土壤，可以按照文献[9]的方法进行处理。

1.2 矩量法基本方程的建立

由于变电站内架空金属导体上电流分布不均匀，本文采用矩量法计算变电站内的电磁场。对于相互连接的复杂导体结构，为了使用矩量法，应当根据导体之间的连接关系和激励源频率将导体分成若干段直线段，并做如下假设：

1）在每段导体中，电流连续变化，并且集中于导体的轴线上。

2）在每段导体表面，线电荷均匀分布。

在导体段的表面，导体内外的电场强度应当满足下面的边界条件

式中，n是圆柱导体表面外法线方向， Ei是施加于导体表面的外电场强度， Es是导体本身轴向电流产生的内电场强度。

由式（5）经过推导[7]，可得

式中，l是圆柱导体的轴线方向，ω是角频率。A是由导体轴向电流 I（l′）引起的矢量磁位，φs是由导体均匀分布的线电荷-∇′I（l′）/（jω）产生的标量电位。本文将轴向电流 I（l’）沿导体表面的变化∇′I（l′）称为漏电流，下面的分析都已漏电流为变量进行分析。将式（6）沿导体轴线积分得

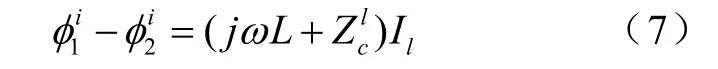
式中，有

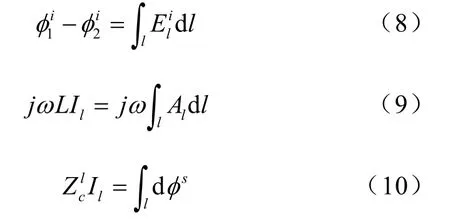
式中，L是导体段的外自感，它等于位于导体轴心的细导线与位于导体表面的细导线之间的电感；是导体段的内自阻抗。由此，导体两端之间的电位差

和导体的轴向电流Il之间将有如下关系

令

则有

对每一段导体，都可以建立上面的等式，最终可以建立方程求解以各导体段上的电流分布情况，进而可以求得各段导体的电位，也可以求得空间任意点的电位分布、电场强度。

1.3 时域计算

按照上面的方法，可以计算给定频率下各段导体上的电流分布，再根据式（6）就可以进一步计算出该频率下空间各点的电场强度。

为了计算变电站故障时的空间瞬态电磁场，我们将上述计算方法与快速傅里叶变换相结合。主要步骤如下：

1）采用快速傅里叶变换算法将激励源的时域波形变换为频域频谱，需要注意的是在时域采样时应满足采样定律。

2）根据激励源的频谱特征，选择适当的计算频率样点。

3）计算各个频率样点对应的单位激励时的导体电流、电压和空间电场强度频率响应。

4）将各个计算频点对应的导体电流、电压和空间电场强度频率响应与激励源的频谱对应相乘，并采用快速傅里叶反变换得到故障过电压时导体电流、电压波过程和空间瞬态电磁场。

依据这一方法编制的计算程序可以用于分析电力系统中变电站内和输电线路附近的三维电场分布。可以考虑土壤的影响，因而可以计及接地部分的影响，适用于电力系统故障频段。

2 算法验证

为了验证本文方法的有效性，应用本文计算方法与与文献[6]和给出的计算方法分别对如下算例进行计算。

设导线长120m，距地面15m，导体半径0.005m。土壤电阻率为 100Ω·m。在导体一端注入峰值为1kV、波形如图 1所示的快速衰减振荡的振铃波类型的电压，另一端接50Ω负载。

图1 注入电压波形

应用本文计算方法和基于文献[4]编写的程序对不同频率下的地面以上 1.5m处导体中点正下方垂直于地面方向的电场强度进行计算，并将其计算结果进行对比，如图2所示。从图2中可以看出在时域波形上，两种方法的计算结果几乎没有差异，事实上，两种计算方法在低于 200kHz的频率时两种方法的计算结果几乎相同,随着计算频率的增加两者偏差开始加大，因此对于频率较低的故障过电压本文的方法是完全适用的。

通过将本文计算方法与其他计算方法计算结果进行对比，表明了本文计算方法的有效性。需要指出的是，本文计算方法不仅可以计算这类简单导体结构产生的空间瞬态电磁场，也可以计算类似于变电站内复杂导体结构产生的空间瞬态电磁场。

图2 导体下方的电场强度对比图

3 变电站内故障过电压情况下空间电场计算

图3为某500kV变电站线路布置简化模型。

图3 某500kV变电站示意图

母线高度20.5m，设备间连线高度9m，设备间连线水平间距为 8m，母线间距 10m。母线半径为6cm，其他导线半径为6.5cm，土壤电阻率取100Ω·m。母线沿Y方向长为147m，设备间连线长为41m。A、B、C三相电压从线路一端注入母线。

3.1 工频电磁环境分析

当变电站正常运行时，站内主要存在频率为50Hz的工频电场和工频磁场。应用本文计算方法对母线和设备间连线下方距地面 1.5m高度处各点的电场强度进行了计算。图4给出了Z方向的电场强度分量。从这幅图中可以得出以下结论：

1）电场强度沿与线路垂直的方向成鞍形分布。

2）设备间连线下方的电场强度要比母线下方的大的多。

图4 Z方向电场强度

距地面 1.5m高度处最大电场强度计算值为9.32kV/m。出现在设备间连线的下方、C相设备间连线附近。

3.2 故障过电压情况下的电场分析

在本文中，只给出了线路故障过电压时的瞬态电磁环境计算结果。计算时假设在A相相位为180°时发生单相接地故障,利用其它故障分析软件得出的线路上的电压波过程作为电源加在导线起点，在计算中将各负载作为集总参数元件连接在图3各架空线路终端。

需要说明的是，在故障情况下，由于最高频率不超过100kHz，即波长低于3km，在变电站外部线路故障时，可以认为变电站内导线上各点电压电流几乎相同，因此也可以将终端开路处理，两种方法计算结果几乎完全相同。

图5给出了故障前后在A相、B相、C相母线上的电压波形。图6给出了母线下方距地面1.5m高平面上电场强度最大点 Z方向电场强度的时域波形，从图中可以看出电场强度达到的瞬时最大值为12.5kV/m，这一值高于稳态运行时的场强值。

图5 三相电压波形

4 结论

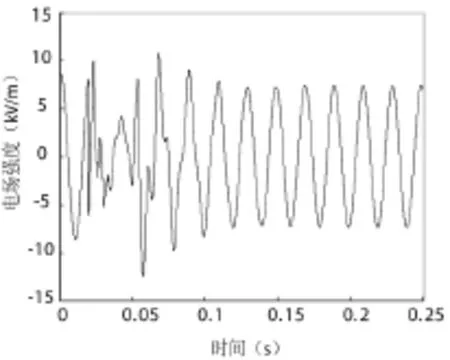
图6 电场强度波形

本文基于矩量法，提出了一种适合于变电站内开关操作时母线、设备间连线、架空线路产生的电磁场的计算方法，可以应用于变电站内故障过电压情况下的电场计算。本文计算方法可以考虑变电站内的复杂导体结构，结合快速傅立叶变换技术，可以实现变电站故障过电压情况下空间瞬态电磁场的预测计算。

[1]EPRI TR 102006: Electromagnetic transients in substations,Vol I、Ⅱ、Ⅲ(M).Palo Alto,CA,1993.

[2]邬雄,万保权,路遥. 1000kV 级交流输电线路电磁环境的研究[J].高电压技术,2006,32(12):55-58.

[3]万保权,邬雄,杨毅波,路遥,张云政.750kV 变电站母线电磁环境参数的试验研究[J].高电压技术,2006, 32(3):57-59,71.

[4]卢铁兵、崔翔.变电站空载母线波过程的数值分析[J].中国电机工程学报,2000, 20(6):39-42.

[5]A. Selby, F. Dawalibi, Determination of current distribution in energized conductors for the computation of electromagnetic fields[J], IEEE Transactions on Power Delivery, 1994, 9(2).

[6]赵志斌,崔翔,张波,李琳,应用矩量法计算变电站内的空间电磁场[J].中国电机工程学报,2004,24(11)：148-153.

[7]Roger F. Harrington, Field Computation by Moment Methods(M), New York, Macmillan, 1968.

[8]张波,崔翔,卢铁兵,李琳,赵志斌.超高压输电线路铁塔附近三维电场的数值计算[J].电网技术,2003, 27(7):5-8.

[9]郭剑,邹军,何金良,韩社教,关志成,水平分层土壤中点电流源格林函数的递推算法[J].中国电机工程学报, 2004, 24(7):101-105.