基于量子粒子群算法的电力系统无功优化
2012-06-22张斌刘幸
张 斌 刘 幸
(1.陕西省地方电力(集团)有限公司延安分公司,陕西 延安 716000;2.华北电力大学,北京 102206)
电力系统无功优化主要是指在不同的条件下,充分使用各种控制手段,来有效达到降低系统功耗,提升电压水平的方法。在数学上,必须使用多目标、多约束、非线性、非连续、混合整数组合,才能达到优化的目的。因为,在计算过程中,需运用到多个连续变量,也需要运用到多个离散变量,使得优化过程十分复杂。
一般而言,常用的优化方法有如下几种:线性规划、非线性规划、二次规划、混合整数法等,每种方法都有其各自的特点和优越性,但缺点也是非常明显的,它们只能对与初始点有关的局部最优解进行搜索,同时,对目标函数和约束条件有连续、可微的要求,耗费时间长,并且时常有“维数灾”的情况发生。与此同时,科技的不断发展和进步,各种先进算法已经成功应用到电力系统的无功优化问题上来,通过多年的实践,已经取得了不错的效果。如粒子群算法、量子算法等。
粒子群优化算法(PSO)[1]是在 1995年由Eberhard和Kennedy等人首先提出,它是一种基于种群搜索的自适应进化计算技术,由于其概念和参数调整简单并容易编程实现,得到了广泛应用,但是PSO算法的早熟收敛问题一直无法破解,因此其应用性受到了一定的限制。
量子计算[2-3]在20世纪90年代中期得到广泛应用,它的最大的优点在于其具有强大计算能力,不少研究者将经典算法和量子算法结合起来进行研究,实现了性能上的突破,如Han提出的量子遗传算法,Sun提出的基于量子行为的粒子群优化算法等。叠加态特性和概率表达特性是量子进化算法的两大特点,叠加态特性最大的特点在于让单个粒子呈现出多种不同的状态,具有种群多样性;概率表达特性帮助粒子以一定概率跳出局部最优解。但是,量子进化算法的编码采用二进制编码,对于数值优化问题由于需要频繁编码解码,加大了计算量;更新策略一般通过既定的查询表实现,没有充分利用进化过程中粒子的协同性。
本文应用的量子粒子群算法[4]基于实数编码,并且融入PSO的更新策略,不仅保持了种群多样性而且大大增加了搜索效率。而且,本文的算法提供了一种量子包容机制,可以包容各种改进的PSO算法。IEEE-30电力系统无功优化测试算例证明了算法的高效性和鲁棒性。
1 数学模型
本文选用网络损耗最小为目标函数[5],控制变量分别为发电机机端电压、变压器分接头位置、并联电容器的投切组数。等式约束包括有功功率以及无功功率的平衡,不等式约束包括节点电压约束,发电机无功约束,电容器无功容量约束等。通过功率流动计算可以自动满足等式约束,同时采用罚函数的方法处理控制变量的上下界,满足不等式约束。
1.1 原始目标函数
无功优化问题描述如下:

1.2 约束条件
潮流约束

电压约束

发电机无功约束
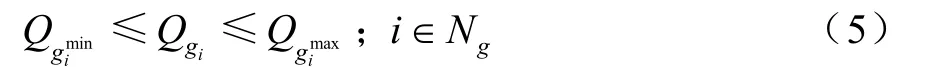
电容器无功约束
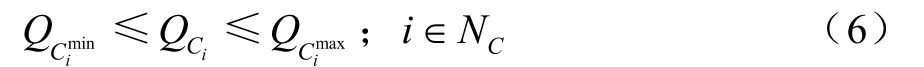
变压器分接头设定约束

线路容量约束

其中,Ploss为系统有功损耗;Pi,Qi分别表示节点i的注入有功功率和无功功率;Gij,Bij分别表示节点i和节点j之间的电导和电纳;Qgi表示节点i接入的无功发电机;Qci表示节点i出补偿电容器的出力;tk表示支路k上变压器分接头的位置;Vi,Vj分别表示节点i和节点j的电压水平;θij表示节点i和节点j的电压相量角;Sl表示通过第l条支路的视在功率;gk表示支路 k的电导;NB表示节点总数;NB-1表示除平衡节点以外的节点总数;NPQ表示 PQ节点总数;Ng表示发电机节点总数;Nc表示补偿电容器投切组数;Nb表示系统支路数;Nt表示包含有载调压变压器的支路总数。
1.3 综合目标函数
综合考虑目标函数和约束条件,引入罚函数处理方法构造目标函数,如下式所示:

在上面的函数中,Vimax、Vimin为节点电压Vi的上限和下限;Vilim、Qilim为i节点电压和无功的限值;Qimax、Qimin为发电机节点无功出力 Qi的上限和下限;α、β分别为违反节点电压约束和违反发电机无功出力约束的节点集合;λ1,λ2为违反电压约束和发电机无功出力约束的惩罚因子。
2 量子粒子群算法
2.1 粒子编码
粒子中的每一位采用量子比特的方式表示,就叫量子位。量子位的状态除了|0>和|1>外,还可以是|0>、|1>的线性组合,通常称其为叠加态,表示为|φ>=α|0>+β|1>。其中,α 和 β是一对复数,称为量子态的概率幅。量子态|φ>因测量或者以|α|^2的概率坍缩到 0,或者以|β|^2的概率坍缩到 1,且满足归一化条件:|α|^2+|β|^2=1。因此,一个量子位可由其概率幅定义为[α, β]T,同理,m个量子位可定义成[αm, βm]T。
本文基于实数编码,直接采用量子位的概率幅作为问题解,采用双链编码方案,如下所示

式中,θij=2π×rand;rand为(0,1)之间随机数;i=1,2,…, m, j=1, 2, …, n;n是种群规模,m是空间维数。由此可见,种群中每个粒子占据解空间中两个位置,分别称为正弦位置和余弦位置。
2.2 解空间变换
不同于传统的量子进化算法,本文直接使用粒子坍塌成某一基本态的概率参与适应度评价。由于粒子的每一维位置向量取值范围不同,因此在计算适应度之前需要对粒子的位置向量进行解空间变换,如式(11)所示。

式中,popuValue为某基本态的概率;a,b分别为第j个粒子第d维的下界与上界;Xjd为第j个粒子第 d维由单位空间[-1,1]n映射到优化问题解空间的值。
2.3 粒子更新
本文为了突出量子概念的优越性,使用基本粒子群算法更新方式。更新策略如式(12)所示。

式中,w为惯性权重,Δθjd(t)为在第t次迭代中第j个粒子第d维的相移量,c1,c2是加速常数,r1,r2是均匀分布的随机数,arctan(pjd)是第j个粒子历史最优值第d维的相位,arctan(yjd)是第j个粒子当前第 d维的相位,arctan(pgd)是全局最优粒子第d维的相位。
根据得到的相移量,计算出量子旋转门,然后更新粒子
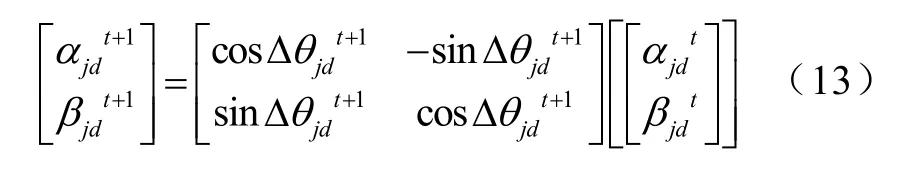
式中,Δθjdt+1为在第 t+1次迭代中第 j个粒子第 d维的相移量,αjdt, βjdt为在第 t次迭代中第 j个粒子第 d维的概率幅,αjdt, βjdt为第 t+1次迭代中第 j个粒子第d维的概率幅。
2.4 算法流程图
量子粒子群算法的流程图如图1所示。
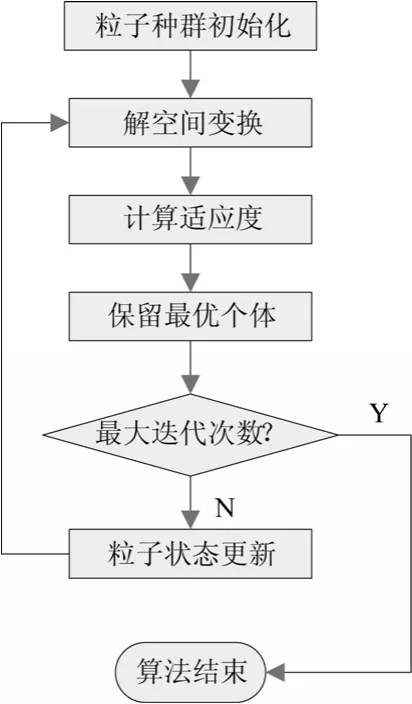
图1 算法流程图
3 基于量子粒子群算法的无功优化
用量子粒子群算法求解无功优化问题时,先对决策变量(发电机机端电压、变压器分接头和无功补偿量)进行量子染色体的编码及种群的初始化,再通过解空间变换,实现量子染色体与决策变量的对应,然后调用潮流计算程序进行目标函数的计算及适应度的评价,保存个体最优信息和全局最优信息,更新量子门,实现种群的进化。
3.1 初始种群的产生
在电力系统无功优化中,各种变量的取值需非常谨慎,万一出现差错,对系统的影响是非常大的。这一点在控制变量上显得尤为突出,在寻找最优解的实践中,笔者发现,很多控制变量取值代表的运行方式对无功优化是毫无用处的。因此,本文采用倾斜分布方式产生初始解群[6]。
第一步,需根据下列三种类型判断初始点的取值范围,本文使用初始粒子种群进行潮流计算。
1)较多节点电压越上限,系统是无功大量过剩状态,需投入感性无功补偿设备、降低发电机的机端电压或切除容性无功补偿设备。
2)较多节点电压越下限,系统是严重缺无功状态,需提高发电机机端电压或投入容性无功补偿设备。
3)少量节点电压越下限或越上限,其余各节点电压稳定,此时处于无功基本平衡。
原则是,分布节点时需在略高于当前值的范围内。
3.2 状态变量的处理
发电机机端电压:按连续量处理,初始运行值在电压指定的上下边界的范围内随机初始化。优化过程中,其值在边界范围内更新;有载变压器和电容器:按离散变量处理,初始运行值在规定的上下限中随机产生。在优化过程中,通过映射编码和取整的方法对离散变量进行处理。对于一个变比调节范围在[Tjmin,Tjmax]之间,共有l个单位分接头的变压器,调节步长为Tstep=(Tjmax-Tjmin)/(l-1),假设第j维控制变量X[j],则令X[j]的取值范围等于分接头的档数,即1≤X[j]≤l。按照Tj=Tjmin+[X[j]-1]Tstep将 X[j]转化为相应的变比值代入目标函数进行计算,其中[.]表示取整。电容器投切组数也按此方法处理。
3.3 电力系统无功优化步骤
本系统优化算法采用基于量子粒子群算法,其主要步骤如下:
1)首先对控制变量的维数及其范围进行设置。设置量子粒子群算法的种群数量 popScale、最大迭代代数iterMax、惯性权重w、自身因子c1、全局因子c2。
2)进行初始潮流计算,根据无功优化的本质按照倾斜分布方式产生原始粒子种群,并设定当前进化代数iter=1。
3)概率幅的初始化。
4)根据式(11)进行解空间变换,然后计算种群适应度。若粒子目前位置优于自身记忆的最优位置,则用目前位置替换;若目前全局最优位置优于已记录的全局最优位置,则用目前全局最优位置替换。
5)根据式(12)对粒子状态更新。
6)判断是否达到最大迭代次数。若是,程序结束。若否,返回第4步。
4 算例
本文采用IEEE-30节点标准系统测试量子粒子群算法的优化结果。首先判断算法是否能执行,分别与传统量子进化算法(QEA)、标准粒子群(PSO)分别比较,编程使用Matlab7.0。
IEEE-30节点具有11个控制变量,包含两个并联电容器节点、6台发电机和4台有载调压变压器。其中变压器上下界分别取1.1和0.9,电容器上下界分别取 0.4和 0。系统负荷 Sload=284.3+j126.2,初始网损为8.324MW。节点和支路数据参见文献[7]。
算法初始参数的设置[8]:种群大小为10;最大迭代次数100代;根据经验加速常数c1和c2取2;惯性权重系数w采用根据迭代次数依次递减的自适应调整法,公式如下:
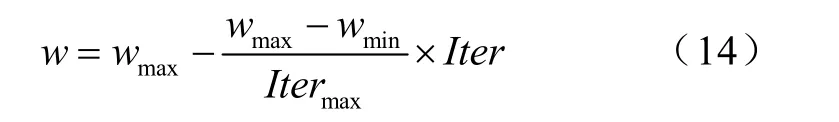
本文采用倾斜分布式启发初始种群产生,因此需要在优化之前了解初始电压情况。

表1 IEEE-30节点初始潮流电压情况
表1为初始潮流的电压情况,优化前有功损失为8.324MW。由表1可以看出,所有节点的电压合格,系统无功基本平衡。如果发电机机端电压初始值为 1.00,将电压划分为 a-e五个区域:a为[1.06,1.10],b 为[1.02,1.06],c 为[0.98,1.02],d 为[0.94,0.98],e为[0.90,0.94]。机端电压初始化为:a区域0%,b区域30%,c区域40%,d区域30%,e区域0%;并联电容器容量设置为0;变压器分接头位置在控制范围内随机产生。
优化前后电压曲线的对比图如图2所示。
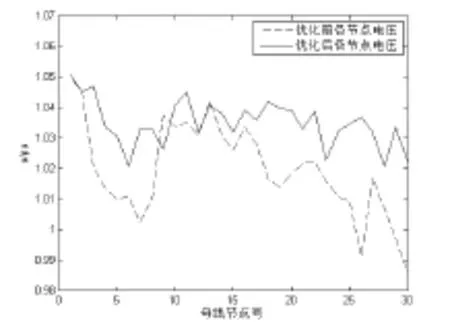
图2 优化前后电压曲线对比图
优化前各节点电压在取值范围内,但是优化以后的电压更加平稳。
分别采用 QPSO、PSO、QEA对电力系统无功优化的结果如表2所示。

表2 QPSO,PSO,QEA结果对比表
由表2分析得知:①采用QPSO进行无功优化后,系统的有功损失为6.732MW,比优化前降低了18.55%,降损效果最为明显。对算法各自测试 100次,其中QPSO和QEA的搜索成功率达到了98%,而PSO成功率只有90%,容易陷入局部最优解;②另外,从表中可以清楚看出,QPSO和QEA的寻优结果明显优于PSO,证明了复杂问题中引入量子概念可以大大改善进化算法,其并行性和概率性既保证了搜索的效率又保证了种群多样性。
图3为QPSO、PSO、QEA在优化过程中粒子分布对比图。

图3 QPSO、PSO、QEA粒子分布对比图
该图是在100次测试中随机选取的一次,对结果分析如下:
1)QPSO既能实现量子算法的并行性搜索,又能考虑到迭代过程中种群全局最优解和自身最优解对寻优的引导性以及粒子之间的协同性,因此寻优速度很快,由图 3(a)可以看出算法在 50代附近已经找到了最优解6.732MW。量子理论还有一个特点是概率性,能保证搜索中种群的多样性,即使搜索后期,仍有粒子分布在离最优解较远位置,防止陷入局部最优。
2)PSO的更新策略是通过记录每次更新后的全局最优值和粒子自身最优值,依赖粒子间信息互动寻求最优解,收敛速度与种群规模相关,一般解决复杂问题需要30~200粒子共同寻优。另外,从图3(b)可以看出,粒子在寻优后期聚集在一起,容易陷入局部最优。
3)图3(c)是传统QEA寻优的粒子分布图。由图可以看出进化过程中粒子分布随机,但是收敛速度很快,在50代附近寻到了最优值。QEA的更新策略是采用查询表的方式[9],比较呆板且无法利用环境信息导致寻优的盲目性。
5 结论
本文采用一种量子粒子群算法解决无功优化问题,结合量子进化算法的叠加态特性和概率表达特性,以及粒子群算法的粒子协同性等优点,算法寻优速度快,鲁棒性强。采用倾斜式启发种群初始化,减少了不可行解的数目,提高了算法效率。通过对IEEE-30典型测试系统的计算分析表明,本文提出的量子粒子群算法在求解大规模电力系统无功优化问题上具有快速、高效、准确的优点,可以尝试用于其他的复杂电力系统优化。
[1]刘建华.粒子群算法的基本理论及其改进研究[D].湖南:中南大学,2009.
[2]李世勇,李盼池.量子计算与量子优化算法[D].哈尔滨:哈尔滨工业大学,2009.
[3]李世勇,李盼池.量子搜索及量子智能优化研究进展[J]. 计算机测量与控制,2009, 17(7).
[4]吕强,陈如清,俞金寿.量子连续粒子群优化算法及其应用[J].系统工程理论与实践,2008,5(5):122-130.
[5]李秀卿,孙守刚,姜世金,许传伟.基于混合优化微分进化算法的电力系统无功优化[J].电力系统保护与控制,2009,37(7):26-29.
[6]张炳才,秦四娟,乔世军,卢志刚.基于改进微分进化算法的电力系统无功优化[J].电力系统保护与控制,2010,38(15):91-94.
[7]靳晓凌,赵建国.基于改进二进制粒子群优化算法的负荷均衡化配电网重构[J].电网技术,2005,29(23):40-43.
[8]周文.粒子群优化算法及其参数设置的研究[J].湖北职业技术学院学报.2006,9(4):93-96.
[9]Hong-mei Ni, Wei-gang Wang. A Niche Quantum Genetic Algorithm Used in Multi-peak Function Optimization [A]. Sixth International Conference on Natural Computation, 2010.
