论Casimir效应中的超光速现象
2012-06-22黄志洵
黄志洵
(中国传媒大学信息工程学院,北京 100024)
论Casimir效应中的超光速现象
黄志洵
(中国传媒大学信息工程学院,北京 100024)
荷兰物理学家Hendrik Casimir于1948年提出存在一种Casimir力——当计算两个互相平行的不带电导体板之间的能量时,当板距d小于真空中虚光子的波长,长波排除,板外的无限多模式大于板内的无限多模式,造成一个小的力量使两板靠近。计算Casimir效应有许多方法,例如可用Green函数描写Casimir能,就可以计算与边界条件对应的4种情况。
可以认为真空中放置双板后改变了真空的结构,故有两种真空:板外的常态真空或自由真空,板间的负能真空。对于与板垂直的电磁波传播而言,真空中的光速并不相同,变化量(△c/c)约为1.6×10-60d-4,故当d=10-9m时△c=10-24c。因此,由于量子电动力学双环效应,K.Scharnhorst断定这会使电磁波的相速和群速大于真空中光速c。虽然超光速的量很小,但却提升了对原理的兴趣。可以说,在发现Casimir效应64年后的今天,它仍使人们感到惊奇。
Casimir力;真空能;负能量;量子场论;量子电动力学;超光速
1 引言
在物理学中,Casimir效应(或说Casimir力)是令人着迷的课题。乍看起来有点令人匪夷所思——一对置于真空中的金属导体板(互相平行),它们之间竟会有仿佛“互相吸引力”的作用,但又不是万有引力。这个力是微小的,但比万有引力却大得多;其存在可由测量而得到证明,不过两板的间距很小时(微米级乃至纳米级)才有可测效应,当然在技术上是非常困难的。H.Casimir[1]的论文发表于 1948年;真正的实验证明者是 S.Lamoreaux[2],论文发表于1997年;两件事的时间差有半个世纪。Casimir的逝世时间是2000年;晚年的他在得知自己的理论得到实验上的确证时,心情的激动是可以想象的。
对Casimir效应的初学者而言,脑海中会产生一系列问题。为什么在经典物理学中不可能有的现象却在量子物理学中出现了?它是否像“量子纠缠态”那样神秘?Casimir当初如何想起这个课题的?什么是Casimir力的本质(为何两板互相吸引而非互相排斥)?Casimir力究竟有多大?这个物理现象的理论意义与实际意义(包括应用前景)是什么?为什么这个效应与负能量(negative energy)概念有联系?为什么在这当中也浮现虚光子(virtual photons)的身影?……诸如此类的疑问令人惊讶。至于这一效应竟然与超光速研究有关,既令人感觉意外又不十分奇怪,因为科学工作者早就认识到事物的联系是非常广泛的,对于一些大自然提供的奇妙现象而言,情况更是如此。
1990 年,德国的 K.Scharnhorst[3]和英国的 G.Barton各在同一刊物上发表文章,声称发现了Casimir效应中的超光速现象(Scharnhorst,Phys.Lett.,B236,1990, 354;Barton,Phys.Lett.,B237,1990,559);这是1990年上半年的事。同年7月,美国的S.Ben-Menahem[4]在同一杂志上发表了题为“双导体板之间的因果性”的论文,对前述两人的工作进行评论。这些文章都是高水平的,例如利用了量子电动力学(QED)概念和Feynman图进行分析。……本文对有关工作的叙述不仅展示了超光速研究的一个方面,也是为了Pervasive through focus(经由专注达到普及);企盼专家学者赐教。
2 对Casimir效应的回顾

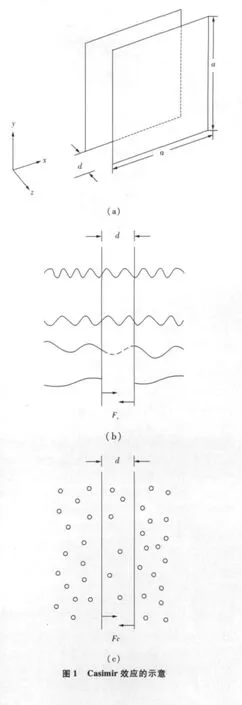
各种研究和计算都是先作一维(1D)分析然后再扩展到三维(3D),前者仅考虑垂直于平板表面的波矢,后者才符合实际情况。为了清晰起见,我们在图1中绘出3个小图;图1(a)表示置于真空中的一对方形金属板(尺寸a×a),互相平行间距为d(假定d≪a);设z轴与板面垂直,板子处于xy平面之中。图1(b)是一维(1D)情况,只有波长λ较小(λ<d)的波才能在板间和板外同时形成;图中显示板间的波动总体上少于板外的波动(长波排除),即有力使Fc板子相互靠近。图1(c)也是对一维(1D)情况的表述,由于板间似乎“排除”掉一些频率较低(波长较长)的光子,板外的较多光子就有使两板有靠近的趋势——但反映真空涨落的是虚光子,它们忽隐忽现、忽生忽灭;图1(c)和图1(b)的描述在本质上是一样的,是波粒二象性的反映。总之,图1的叙述方式易于理解。
早在上世纪40年代初就已发现,处在理想导体壁腔体中的原子会被腔壁吸引,形成Casimir-Polder力[7]。在 N.Bohr的启发下,H.Casimir(1909-2000)利用零点能(ZPE)观念对腔体内的状况重作计算[1];他采用两块理想导体板平行对称放置构成开腔,以计算边界条件变化时ZPE发生的变化:

式中E1是无板(无腔体)时的ZPE,E2是有板(有腔体)时的ZPE,Ec是专有的 Casimir能(E2与之 E1差)。故若算出Ec≠0即表示置入腔后ZPE发生了变化;若Ec<0,表示置入腔后ZPE变小了。
为了计算Casimir效应,必须算出两板之间(体积a2d)所含振动模数目。以图1(a)为基础进行讨论;分析方法是经典场论结合量子场论(QFT)。我们知道真空态是在任何模式均无光子的态,即对所有波矢及波长λ均有n=0,这里n是表征光子场的光子数态;这时可证明真空能基本方程为

式中ħ是归一化Planck常数,ωk是对应波矢k→的波频(角频率)。上式没有在讨论ZPE时常出现的系数1/2,原因是存在两种横向线极化状态(TE和TM),每种波都乘以2。现在考虑空间有一维系统,即图1(b)或图1(c),对应 k=kz的波模,在板处(金属表面)应为波节,kz应为离散值(k=kz=nπ/d),造成一系列分立模式,故可写出腔的真空能(ZPE)为

式中c是真空中光速;同一空间没有腔体时分立的n应为连续变量:


负号表示Casimir能是负能量。
在物理学中,做功 W→= ʃF→·dl→(力对距离元乘积的积分),而功又可表为能量差;由此看出能量与功等效。反过来说,能量对距离的变化呈现出力效应;故有

在一维条件下求出Casimir力为

然而真实情况是图1(a),在3D分析中必须包含波矢不与板垂直的那些模。这时可导出以下算式:

通过在Euler-Mclaurin求和公式中引用3阶导数,可以证明

实际上(9)式的花括号内的两项,每项都是发散的,但差值却不是发散的——这是最奇妙之处。现在使用(7)式求出

此即Casimir力公式;可见Fc∝a2(板面积越大力越大),而且Fc∝d-4(间距越小力越大)。前者的原因可理解为板面积越大则内外光子数差别越发显著,后者的原因可理解为d越小则板间允许的模数越小(光子越少),造成力变大。……注意Casimir力与Newton万有引力的不同,后者的规律是Fc∝d-2,且力的大小与两板质量乘积成正比(F∝m2)。但对Casimir力而言,Fc与金属板质量毫无关系。
由(11)式,金属板受到的压强为

取Fc的量纲为 dyne,a的量纲为 cm,d的量纲为μm,这时有
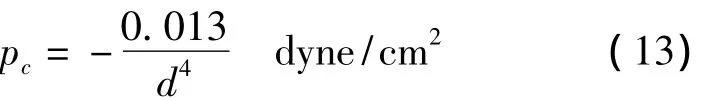
若d=1μm,a=1cm,则有 Fc=-1.3×10-2dyne=-1.3×10-7N;也就是说,两个面积1平方厘米、相距1微米的板之间的Casimir力的绝对值大约比10-7N大一点点,大约相当于一个直径0.5mm的水珠所受的重力。这种力很小,但若把d大大减小则可能很可观(必须注意到当d→0时,|Fc|→∞)。实际上,若d=10nm,pc≅1atm(一个大气压);故在纳米世界中这个力不可忽视,或许比Newton引力的重要性大得多。
关于Casimir效应的真正有意义的实验是始于S.Lamoreaux[2](1997 年),证明 Casimir力确实存在。但其实验被认为有若干不确定性[8],因而首次精确测量Casimir力的实验被认为是U.Mohideen[9](1998年);图2是一个测量实例(转引自 G.L.Klimchitskaya等[8]),d 表示两个铝(Al)表面的间距,纵坐标Fc是以10-12N为单位;虚线是理想金属表面(无趋肤效应、理想光滑)的计算,实线是实际金属表面(有趋肤效应、非理想光滑)的计算,小圆圈是测量结果。可见,Fc是非常微小(故难于检测)的力。但它确实是存在的。
近年来笔者就 Casimir效应写过一些文章[10,11],因为对这一现象的理解关系到当代科学技术发展的许多重大问题。图3是本文所设计和绘制的学科关系,实线表示“有密切联系”,虚线表示“有联系”。过去笔者未论述过Casimir效应与超光速研究的联系;本文的内容是对此缺憾的弥补。众所周知,狭义相对论(SR)认为超光速是不可能的,但量子理论不为速度规定上限。“Casimir效应中有超光速现象”的论据,应看作是量子理论范畴中的观点,并不令人奇怪。

3 与Casimir效应相关联的超光速现象
从经典物理的角度看,“真空”是什么都没有的虚空,“真空”也只有这一种。但从量子物理的角度看,如在真空中放进两块平行金属板,板子的内、外的状态并不相同——两板之间的真空程度更高、更深,所以才有力量使两板有靠近的趋势。这个Casimir效应既已被实验所证明,我们就得承认上述“两种真空”的说法是正确的。既如此,“板内和板外的光速可能不一样”就是合乎逻辑的了。因此,正是边界条件的改变影响了真空,从而影响了电磁波的传播速度。换言之,光的传播是取决于真空的结构,而“真空有结构”正是量子物理学的基本观点。正是由于Casimir效应,我们才得以区分以下两者:①常态真空(usual vacuum)也叫自由真空(free vacuum);②有板时的板间真空(vacuum between the plates);后者的特征是 vacuum energy density reduced,故笔者认为也可称为负能真空(negative energy vacuum),这是发生超光速现象的物理基础。
Casimir效应型结构(双平行板)是把边界条件强加到光子真空涨落上,这时可用量子电动力学(QED)来考虑问题。1990 年 K.Scharnhorst[3]对此作了双环修正(two-loop corrections)计算,根据QED有效作用发现,对于处在真空中的双板,考虑与板垂直的光传播时,光速会发生改变。Scharnhorst虽然发现这种“改变”是光速增大了(进入超光速区),但他谨慎地避免使用fast-than-light或superluminal之类的用语。图4是作QED计算时的双环图(twoloop diagram),它对光子极化算子(photon polarization operator)作出贡献,因而对折射率n的计算作出贡献。

图4 QED计算中的双环图
Scharnhorst的分析计算集中到一点——先在垂直于板面方向上计算折射率:

式中ε11、μ11是介电常数张量分量和导磁率张量分量,n的下标p代表perpendicular;最终导出

式中d是两块理想导电平板的间距,m是质量;规定c0为常态真空或自由真空中的光速,则有

式中c是在板间真空条件下在板面垂直方向上的光速,c与c0不同是由于真空的结构性改变(change in the vacuum structure),这改变是由置入双板造成的。结果是c>c0;这里 c0=299792458 m/s,c大于 c0即超光速。进一步的计算给出:
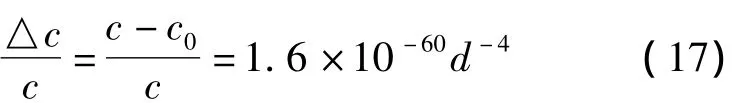
取 d=1μm,△c/c=1.6 ×10-36,是非常小的;但即便如此也与狭义相对论(SR)不一致——无论超过光速的量多么微小,均为SR理论所不容。可以尝试再次减小d,——对于1纳米间隙(d=1nm),增量△c=10-24c。这个数值也非常小,但在某些情况下有重要性;在特定的宇宙学条件下,例如在宇宙弦(cosmic string)的附近——这是说假如它们存在的话,引起的效应会显著得多。总之,Scharnhorst并未计算“光子在两块金属板之间的飞行速度”,而是计算两板间波垂直传播时的波速,发现相速比光速略大(vp>c)。在频率不高条件下讨论,可以忽略色散,群速等于相速,故群速比光速略大(vg>c)。我们知道在用作微波传输线的波导(横截面为矩形或圆形的金属管子)中,相速就是大于光速,毫不奇怪;但波导中群速总小于光速(vg>c)。因此Scharnhorst的主要成果是证明了在Casimir效应中有超光速群速出现,而这并不是随便就会有的现象。
1993 年 G.Barton 和 K.Scharnhorst[12]称两块金属平板为“平行双反射镜”(parallel mirrors),重新解释有关问题。论文题目有趣但令人费解——“平行双反射镜之间的量子电动力学:光信号比c快,或由真空所放大”(“QED between parallel mirrors:light signals faster than c,or amplified by the vacuum”)。文章的摘要说:
“由于量子化场的散射,在两个平行双反射镜之间垂直穿行的频率为ω的光,所经历的真空是折射率为n(ω)的色散媒质。我们早先的低频结果表示n(0)<1,是结合了Kramers-Kroning色散关系和经典的Sommerfeld-Brillouin论据,以宣示两者之中任一情况:①n(∞)<1,因而信号速度c/n(∞)>c;②n的虚部为负,反射镜间的真空不足以像一种正常无源媒质那样对光探测作出响应。”因此很明显,两作者关注的是真空的性质;他们认为在Casimir效应的物理情况和条件下,真空的折射率不再等于1,而可能比1要小。当然这仍是QFT的观点,与经典物理学不同。另外,应当注意Scharnhorst的“群速超光速”有两个条件,一是专指垂直于板面的波,二是频率不太高(ωme)。
为什么在Casimir效应赖以发生的两块金属板之间会发生电磁波速比c大的现象?从概念上讲,在两个平行板反射镜(距离d)之间,考虑绝对温度为零时的Maxwell电磁场,板子假定在任何频率均为理想导体。板子外边界条件为E11=0、B⊥=0。若场是量子化的,其真空结构不同于无边界空间中的情况。特别是,场分量平方、能量密度不同——后者较低,一如Casimir效应所证明了的。
众所周知,即使没有反射镜,Dirac的电子/质子场的零点振动深刻改变真空性质,这是QED相对于经典物理的区别。例如,它们向Maxwell方程引入非线性,随之发生了光散射。这些非线性结合反射镜感应改变了零点Maxwell场,造成反射镜之间的与镜垂直的光速度可能超过c;虽然超光速程度很少难于观察,但却提升了对原理的兴趣。
总之,B&S文章重点在于对低频折射率的考虑,得到相速、群速超过c。在两个反射镜之间,相对于无界空间,平面波探测传播是改变了(由探测场的费米子感应耦合到量子化Maxwell场的零点振荡)。当ω≪me,对Maxwell方程的非线性修正可归结为Euler-Heisenberg有效拉氏量密度:

由此出发的研究表明,对于反射镜间的垂直传播而言,有效折射率变为

而与反射镜平行的传播的折射率仍为1,与无界空间相同。

对于实际测量而言,△n是太小的;它其实就是

△ε、△μ或可理解为介电常数、导磁率随位置的变化。
4 讨论
从表面上看,超光速研究只是无数科学技术课题之一,正如昆虫学家研究蜘蛛,或者苹果公司的Jobs在生前设计iPhone和iPad产品,性质是相同的。然而笔者认为,超光速研究是探索人类心灵深处的某种追寻。一些科学家的反对或逃避只是一种想使自己避免思想混乱的本能反应,潜意识中重视的已不是对真理的追求,而是极力维护学术界的现存秩序。……有人说“今天‘我们的已有知识’全经过了严格的理性审查”,这样讲是在无比丰富复杂的大自然面前缺乏应有的谦虚。
1997年美国物理学家 P.Gibbs[13]指出:“在将来的更完备的物理理论中,不能保证光速仍然具有速度极限的意义”(“there is no guarantee that light speed will be meaningful as a speed limit in a more complete theory of the future”)。他这样讲是有充分理由的;我们知道,人们认为迄今为止所有已知的物理现象(除引力外)均符合粒子物理学中的标准模型(standard model),而该模型是一个相对论性量子场论(relativistic quantum field theory),描述包括电磁相互作用、弱相互作用、强相互作用在内的基本物理过程和所有已观测粒子。根据这个理论,任何对应于两个在有类空距离的事件处所作物理观测的算子是对易的。然而,尽管从原则上讲在标准模型中这些物理作用不能以超光速传播,却缺少对标准模型的量子场论的自冾性的完整严格的证明——很可能它不是自冾的!也就是说,在任何情况下都没有这种保证:不会有其他未发现的粒子和力是不遵守其规则;此外,也无人将其推广到包括广义相对论(GR)和引力。许多在量子引力方面进行工作的物理学家怀疑,关于因果性和局域性的如此简单的多个表达式能否作这样的普遍化。……因此我们可以说,当前仍有一些科学家热衷于超光速研究是不奇怪的。
2010年笔者提出要重视量子超光速性(quantum superluminality)的研究[18];现在我们可以说,它主要包含3方面:①量子隧穿的超光速性[14-18];②量子纠缠态的超光速性[19];③Casimir效应中的超光速性[3,12]。这些都植根于量子理论的非局域性(non-locality)物理哲学思想,既是重要的也是非常有趣的。
[1]Casimir H.On the attraction between two perfect conducting plates[J].Proc Ned Akad Wet,1948,51:793 ~797.
[2]Lamoreaux S K.Demonstration of the Casimir force in the 0.6 to 6μm range[J].Phys Rev Lett,1997,78:5-8.
[3]Scharnhorst K.On propagation of light in the vacuum between plates[J].Phys Lett,B,1990,236(3):354-359.
[4]Ben Menahem S.Causality between conducting plates[J].Phys Lett,B,1990,250:133(1-13)
[5]Bordag M.The Casimir offect for a sphere and a cylinder in front of plane and corrections to the proximity force theorem[J].Phys Rev D,2006,73:125018.
[6]邱为钢.卡西米尔效应的格林函数计算方法[J]. 大学物理,2010,29(3):33-34.
[7]Casimir H.Polder D.The influence of retardation on the London-van der Waals forces[J].Phys Rev 1948,73(4):360-372.
[8]Klimchitskaya G.The Casimir force between the materials:experiment and theory[J].Rev Mod Phys,2009,81:1827-1885.
[9]Mohideen U,Roy A.Precision measurement of the Casimir force from 0.1 to 0.9μm[J].Phys Rev Lett,1998,81:4549-4552.
[10]黄志洵.论零点振动能与Casimir力[J].中国工程科学,2008,10(5):63-69.
[11]黄志洵.真空涨落与Casimir力[J].中国传媒大学学报(自然科学版),2010,17(3):1-7.
[12]Barton G,Scharnhorst K.QED between parallel mirrors:light signals faster than light,or amplified by the vacuum[J].J Phys A:Math Gen,1993,26:2037-2046.
[13]Gibbs P.Is faster than light travel or communication possible?[EB/OL].http:math.ucr.edu/home/baez/physics/relativity/speed of light/FTL.html,1997.
[14]黄志洵.波导截止现象的量子类比[J].电子科学学刊,1985,7(3):232-237.
[15]Enders A,Nimtz G.On Superluminal barrier traversal[J].J Phys I France,1992,(2):1693-1698.(又见:Nimtz G,Heitmann W.Superluminal photonic tunneling and quantum electronics[J].Prog Quant Electr,1997,21(2):81-108.)
[16]Steinberg A M,Kuwiat P G,Chiao R Y.Measurement of the single photon tunneling time[J].Phys Rev Lett,1993,71(5):708 ~ 711.(又见:Grunter T,Welsch D G.Photon tunneling through absorbing dielectric barriers[J].ar Xiv:quantph/9606008,1996,1(6):1-5.)
[17]黄志洵.超光速研究的量子力学基础[J].中国工程科学,2004,6(4):15-25.
[18]黄志洵.超光速实验的一个新方案[J].前沿科学,2010,4(3):41-62.
[19]Gisin N,et al.Optical test of quantum non-locality:from EPR-Bell tests towards experiments with moving observers[J].Ann Phys 2000,9:831-841.(又见:Salart D,et al.Testing the speed of“spooky action at a distance”[J].Nature,2008,454(Aug 14):861-864.)
Faster-than-light Phenomenon of the Casimir Effect
HUANG Zhi-Xun
(Communication University of China,Beijing 100024)
The Casimir force was predicted in 1948 by Dutch physicist Hendrik Casimir,he realized that when calculating the energy between two parallel uncharged conducting plates,only those virtual photons whose wavelengths fit an integral number of times into the gap should be counted.Each mode contributes to a pressure on the plates,and the infinite number of modes outside the plates is greater than the infinite number inside the plates,resulting in a small force drawing the plates together.There are many methods to calculate the Casimir effect.For example,the Green function expression of the Casimir energy was applied,and the Casimir energy between the plates with four kinds of boundary condition was calculated by using that method.
Then,we say that the change in the vacuum structure enforced by the plates.There are two kinds of vacuum,one is usual vacuum or free vacuum(outside the plates).Another is the negative energy vacuum(inside the plates).They cause a change in the light speed for electromagnetic waves propagating perpendicular to the plates:△c/c≅1.6 ×10-60d-4,and d is the plate distance.When d=10-9m(1nm),△c=10-24c.Then,a two-loop QED effect,uncovered by K.Scharnhorst,cause the phase and group velocities of an electromagnetic wave to slightly exceed c.Though the difference are too small,that raise interesting matters of principle——Casimir effect still surprising after 64 years.
book=2,ebook=331
Casimir force;vacuum energy;negative energy;quantum field theory(QFT);quantum electro-dynamics(QED)
O412
A
1673-4793(2012)02-0001-08
2012-02-28
黄志洵(1936-),男(汉族),北京市人,中国传媒大学教授、博士生导师,中国科学院电子学研究所客座研究员。
Euler-Mclaurin求和公式后得到
(责任编辑
:龙学锋)
