Code顶点算子代数的实现

付佳媛，陈燕

(中国传媒大学理学院，北京 100024)

Code顶点算子代数的实现

付佳媛，陈燕

(中国传媒大学理学院，北京 100024)

利用Virasoro代数的酉表示构造了一个Code顶点算子代数，给出了Code顶点算子代数的一个实现。

Code顶点算子代数;顶点算子;Virasoro代数的酉表示

1 预备知识

本节中我们将给出顶点算子代数的定义以及某些不可约表示的性质.首先我们介绍几个符合:

(1)N，Z+，Z，C分别表示非负整数集，正整数集，整数集，复数集.

(2)R是一个线性空间，定义如下符合:

定义1.1 一个Z-阶化的向量空间V=⊕n∈ZVn，其齐次空间都是有限维的，即dimVn＜∞，∀n∈Z，并且在V上定义了一个算子Y(称为顶点算子):

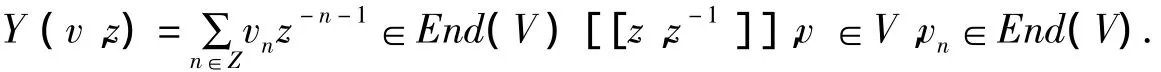
如果V满足以下条件:

(1)存在一个元素1∈V0，称为真空元，满足

(1.1)Y(1，z)=1V(1V:V上的恒等映射);

(1.2)v-11=v，vn1=0，对于所有的 n≥0.

(2)存在一个元素ω∈V2，称为Virasoro元素，满足(2.1){L(n):=ωn+1}是Virasoro代数的生成元，即满足Virasoro关系:

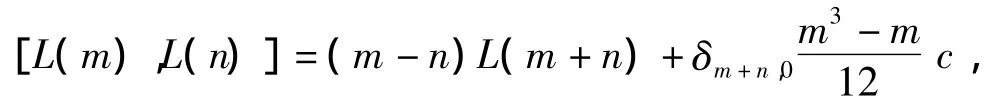
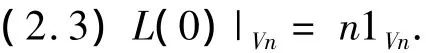
(3)交换性:对于任意的v，w∈V，总存在n∈N，使得

成立.我们称(V，Y，ω，1)为顶点算子代数.

下面回忆Virasoro代数及其酉表示.对于李代数L={L(m)|m∈Z}，如果满足如下关系

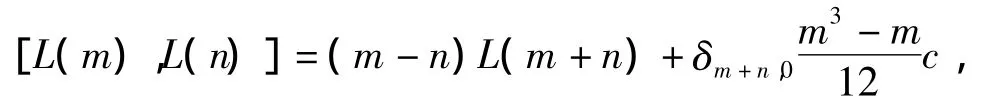
这里c∈C称为V的central charge.

(2.2)L(-1)-导子性质:

则称L为Virasoro代数，c称为其central charge.

我们知道Virasoro代数的不可约表示L(c，h)有如下性质:

2 Code顶点算子代数的定义

n∈N，使得

其中Mi，i=1，2…，n均为超顶点算子代数.字义其上的顶点算子为:

并线性扩张到整个M^上，其中vi∈Mi，Y^i为Mi，i=1，2，…，n，上定义的超顶点算子.易证如此定义的M^是一个超顶点算子代数.

3 Code顶点算子代数的实现

证明 由引理3.3易求得:

同样通过计算可以得到如下关系:

从而我们有如下定理:

定理3.5 Vδ是如上定义的Virasoro代数的酉表示.

定理3.7 MD是一个code顶点算子代数.

证明 由顶点算子代数的定义、Virasoro的酉表示U以及U的外积U∧r的构造可得MD=(U∧r)0是一个code顶点算子代数.

［1］Masahiko Miyamoto.Representation Theory of Code Vertex Operator Algebra［J］.J Algebra，1998，201:115-150.

［2］Chongying Dong，Robert L Griess Jr，Gerald Hohn.Framed Vertex Operator Algebras，Codes and the Moonshine Module［J］.Comm Math Phys，1998，193:407-448.

［3］James Lepowsky，Haisheng Li.Introduction to Vertex Operator Algebras and Their Representations［J］.Progress in Mathematics，2003，227.

A Realization of Code Vertex Operator Algebra

FU Jia-yuan，CHEN Yan
(Department of Mathematics，Communication University of China，Beijing 100024 China)

We construct a Code Vertex operator algebra by the unitary representation of Virasoro algebra.

code vertex operator algebra;vertex operator;unitary representation of virasoro algebra

O152.5

A

1673-4793(2012)02-0022-07

2012-02-29

国家自然科学基金资助项目(10901146);中国传媒大学382人才工程项目

付佳媛(1978-)，女(汉族)，黑龙江哈尔滨人，中国传媒大学教授.E-mail:fujy@cuc.edu.cn

(责任编辑

:王 谦)