面向重心变化的自适应飞行控制系统设计

张 晶 申功璋 杨凌宇

（北京航空航天大学 飞行器控制一体化技术重点实验室，北京 100191）

面向重心变化的自适应飞行控制系统设计

张 晶 申功璋 杨凌宇

（北京航空航天大学 飞行器控制一体化技术重点实验室，北京 100191）

重心的变化直接影响飞机本身的控制特性，使得控制系统设计更为复杂.针对已有方法模型依赖性强、鲁棒性差的局限性，提出了一种面向重心变化的非线性自适应飞行控制系统设计方法.该方法基于逆动力学理论和重心在线估计系统设计标称控制律，在此基础上引入自适应滑模控制单元来构建自适应补偿控制律，其中滑模控制用于保证控制的鲁棒性和稳定性，而自适应单元则通过对模型不确定性和重心估计误差的估计及补偿提高控制的适应性和控制性能.结合Lyapunov稳定性理论证明了闭环系统的稳定性.仿真结果表明:该方法能有效地实现对系统未知不确定因素的补偿，具有较强的鲁棒性.

飞行控制系统;自适应控制系统;滑模控制;重心

飞机飞行中诸多因素均会不同程度地影响重心位置，使重心发生偏移，而重心的变化进一步影响了飞机本身的控制特性［1］.针对飞机在重心变化下的控制问题，传统的增益调参方法［2］需要增加对重心参数的调节，控制律的设计更为复杂、繁琐，且各平衡点间的参数调节缺乏规律性.文献［1，3］提出了一种基于逆动力学和重心估计的飞行控制方法，能有效地利用重心在线估计信息，适应飞机因重心改变而引起的运动特性的变化.但是，该方法依赖于精确的飞机非线性数学模型和准确的重心估计数据，当系统存在建模误差、重心估计误差、外界干扰及其它未知不确定因素时，该方法的控制性能变差甚至失效.

本文针对上述方法的优缺点，提出一种面向重心变化的非线性自适应飞行控制系统设计方法，以逆动力学解算为基础，通过设计滑模控制律保证控制的鲁棒性和稳定性;然而滑模控制中切换项增益过小将影响控制的鲁棒性，过大则导致严重的抖振，因此在滑模控制的基础上引入自适应单元对系统的不确定因素进行估计和补偿，减小甚至消除未知不确定性对系统的影响，从而使系统具有一定程度的在线学习能力，并在控制过程中根据控制效果在线调整控制输出，提高控制的适应性及控制性能.

1 总体方案

由于重心偏移对飞机运动特性产生了直接的影响，因此首先建立考虑重心偏移的飞机动力学模型;在此基础上设计基于逆动力学解算和自适应补偿的飞行控制律，减小重心估计误差、未建模动态等不确定性对控制性能的影响，使飞机在不同重心下具有良好的飞行性能.基于此，本文构建姿态控制系统总体方案如图1所示.

图1 基于逆动力学解算和自适应补偿的姿态控制系统

在图1中，姿态控制系统由姿态控制器、气动舵面指令解算和重心在线估计组成.

姿态控制器包括逆动力学解算和自适应补偿两部分.假定先不考虑建模误差、重心估计误差等系统不确定性，由自然频率、阻尼比构造姿态角的期望动态特性，根据动力学方程的逆特性和重心在线估计值解算得到合外力矩的需求，即标称控制律;在此基础上，引入自适应单元对模型不确定性和重心估计误差进行在线估计，并结合滑模控制获得自适应补偿控制律.

气动舵面指令解算和重心在线估计模块的设计详见参考文献［1］.

2 考虑重心偏移的飞机动力学模型

假设飞机为刚体，且地面坐标系为惯性坐标系［4］，机体固连坐标系为动坐标系［1］.定义现时刻重心相对于初始重心位置的偏移量为Δr，动坐标系角速度为ω，原点处的惯性速度为vO.

vO，ω 和 Δr可分解为

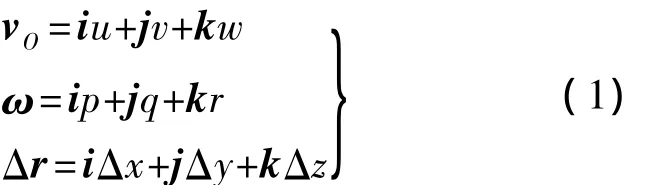
式中，i，j，k 分别为动坐标系 xb，yb和 zb轴的单位向量;[u，v，w]T，[p，q，r]T，[ Δ x，Δy，Δz]T分别为vO，ω，Δr在动坐标系的分量.

同上，合外力F和合外力矩M可表示为

式中，X，Y，[]ZT，L，M，[]NT为F，M在动坐标系的分量.

由牛顿第二定律和动量矩定义，用微元法可推导考虑重心偏移的飞机在合外力作用下的线运动方程和在合外力矩作用下的角运动方程［1，5］:

式中，m 为飞机质量;Ix，Iy，Iz分别为绕 xb，yb和 zb轴的转动惯量;Ixy，Iyz，Ixz为惯性积.

3 自适应飞行控制系统设计

3.1 非线性系统描述

对于式（3）所示的力矩方程，可简记为

别为滚转角、俯仰角、偏航角.

对式（5）求导可得

将式（6）代入式（4）可得

式中，C为单位阵，且

3.2 姿态控制器设计

设计姿态控制器，使X（t）渐近跟踪期望值Xc（t），且对建模误差、重心估计误差及外部扰动有较强的鲁棒性.定义跟踪误差e=Xc－X.

3.2.1 逆动力学解算

先不考虑建模误差、重心估计误差等系统不确定性，设计标称控制律u1.

合外力矩对飞机姿态运动的影响体现为姿态角的二阶导数，将姿态角的期望动态特性构造为二阶线性形式，用自然频率、阻尼比进行定量描述.设计虚拟控制为

式中，vX为虚拟控制量;ωn=［ωn1，ωn2，ωn3］T，ξ=［ξ1，ξ2，ξ3］T为期望的自然频率和阻尼比.

根据逆动力学理论，可得标称控制律为

3.2.2 自适应控制律设计

除标称控制律外，为克服未建模动态、重心估计误差等不确定因素的影响，设计自适应补偿控制律u2.

因系统相对阶为2，设计积分型切换面为

式中，κ1，κ2的对角元素为严格正常数.

将S对时间t微分可得

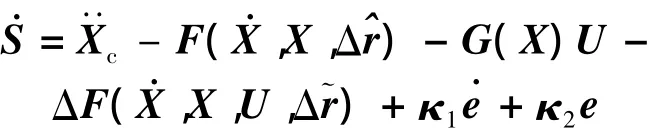
由U=u1+u2，将式（10）和式（11）代入上式可得

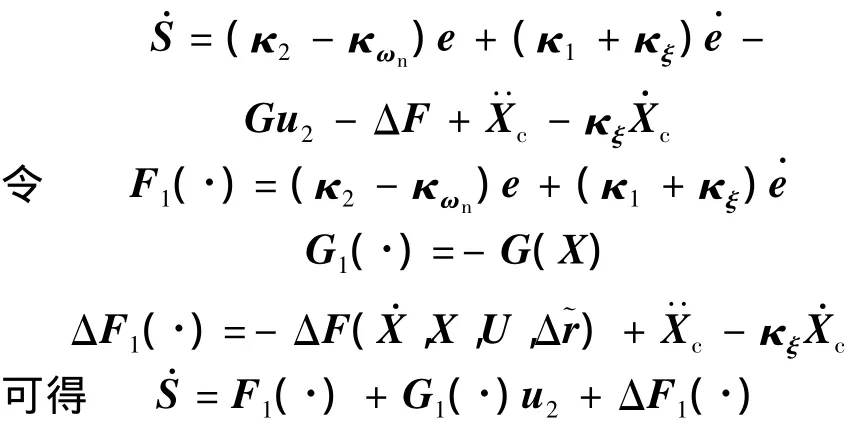
式中，F1（·）和 G1（·）均已知，ΔF1（·）未知，具有不确定性［6］.

假设1 对任意的X（t），G1（·）可逆;

假设2 系统的不确定性ΔF1（·）满足［7］:

式中，α的元素为正常数.

设计如式（13）所示的自适应控制律，可证明能实现闭环系统的稳定控制:

3.2.3 系统稳定性分析

定理1 若系统满足假设1和假设2，采用如式（13）所示的控制律和式（14）所示的参数自适应调整律，则系统状态将在有限时间内达到滑模面，并保证输出跟踪期望值:

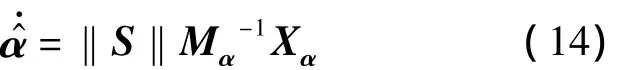
式中，Mα=MαT＞0.证明 取Lyapunov函数:

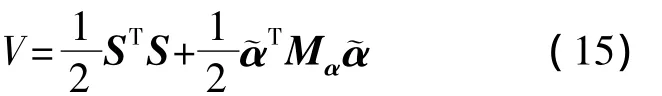
由式（12）和式（15）可得

将式（13）和式（14）代入化简得

因此，系统状态能在有限时间内达到滑模面S=0，并实现系统输出渐近跟踪期望值.

综合式（11）和式（13），姿态控制律为

4 仿真分析

为验证本文控制系统的有效性，以某型飞机为对象进行了仿真.飞机的初始状态为:高度为11 km，飞行速度为 236 m/s，θ=4.2°，飞机的初始重心为0.28cA，cA为平均气动弦长.选取期望的阻尼比和自然频率为 ξ=［1.1，1.0，1.1］T，ωn=［4.0，3.4，4.0］T.以重心估计偏差作为未知不确定因素，分别基于如下的设定条件进行仿真分析.

1）在俯仰和滚转通道施加10°方波指令，在第3s加入重心偏移量Δx=－0.5m，Δy=0m，Δz=0 m，重心估计误差50%;

2）在俯仰和滚转通道施加10°方波指令，在第3s加入重心偏移量 Δx=－0.5 m，Δy=0.1 m，Δz=0.1 m，重心估计误差70%.

将本文方法与逆动力学方法进行对比分析，姿态响应曲线如图2和图3所示.

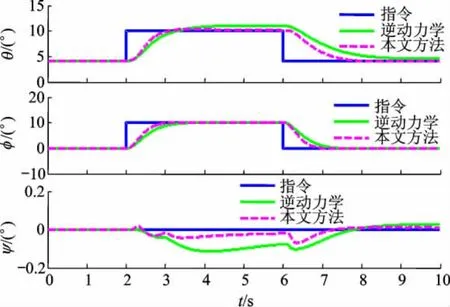
图2 仿真条件1的姿态响应对比曲线

图3 仿真条件2的姿态响应对比曲线

由图2、图3可知，仿真条件1下，重心纵向偏移量为Δx=－0.5 m，且系统存在50%的重心估计误差，无自适应补偿的逆动力学方法的控制效果明显变差，特别是俯仰通道，响应跟踪指令的能力减弱;而采用本文方法，通过在滑模控制的基础上引入自适应单元实现了对系统未知不确定因素的补偿，重心估计误差并未对控制系统造成明显的影响，各通道响应都能较好地跟踪指令，快速性好，通道间耦合小，体现了控制系统的适应性和稳定性.仿真条件2下，重心纵向、侧向和垂向偏移量分别为 Δx=－0.5 m，Δy=0.1 m 和 Δz=0.1 m，与仿真1结果类似，系统在70%重心估计误差条件下，各通道均具有较好的控制效果，优于无自适应补偿的逆动力学方法，系统具有一定的鲁棒性.

5 结论

本文提出了一种面向重心变化的非线性自适应飞行控制系统设计方法，能有效综合逆动力学理论、滑模控制及自适应控制的优点.逆动力学方法物理概念清晰、应用简便，不涉及复杂的气动特性;自适应滑模控制律中的自适应单元能对建模误差、重心估计误差等不确定因素进行估计和补偿，减小甚至消除未知不确定性对系统的影响，从而在一定程度上提高了控制的适应性和控制性能.仿真结果表明:该方法在系统存在未知不确定性时仍具有良好的控制效果，鲁棒性强.

该方法设计时需调节的参数较多，且在不同重心位置时的参数调节缺乏一定的规律性，如何从理论上找到一种适应性的参数整定方法还有待于进一步深入研究.

（References）

［1］张晶，申功璋，杨凌宇.基于逆动力学和重心估计的飞行控制系统设计［J］.北京航空航天大学学报，2009，35（11）:1315－1319

Zhang Jing，Shen Gongzhang，Yang Lingyu.Design of flight control system based on inverse dynamics and center of gravity estimation［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35（11）:1315－1319（in Chinese）

［2］Nguyen N，Krishnakumar K，Kaneshige J，et al.Dynamics and adaptive control for stability recovery 1of damaged asymmetric aircraft［R］.AIAA-2006-6049，2006

［3］Zhang J，Yang L Y，Shen G Z.Modeling and attitude control of aircraft with center of gravity variations［C］//Proceedings of the 2009 IEEE Aerospace Conference.Piscataway，NJ:IEEE Inc，2009

［4］吴森堂，费玉华.飞行控制系统［M］.北京:北京航空航天大学出版社，2005:8－11

Wu Sentang，Fei Yuhua.Flight control system［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，2005:8－11（in Chinese）

［5］Bacon B J，Gregory I M.General equations of motion for a damaged asymmetric aircraft［R］.AIAA-2007-6306，2007

［6］Hall C E，Shtessel Y B.Sliding mode disturbance observer-based control fora reusable launch vehicle［R］.AIAA-2005-6145，2005

［7］刘春生，姜斌.含有输入动特性不确定飞控系统的自适应滑模控制［J］.应用科学学报，2009，27（4）:419－424

Liu Chunsheng，Jiang Bin.Adaptive sliding-mode control for uncertain flight system with actuator dynamics［J］.Journal of Applied Sciences，2009，27（4）:419－424（in Chinese）

Design of adaptive flight control system for aircraft with center of gravity variations

Zhang Jing Shen Gongzhang Yang Lingyu
（Science and Technology on Aircraft Control Laboratory，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

Due to the center of gravity varying over a specific range，the aircraft may deviate from its known dynamics，thus bringing special problems to the attitude control system.To overcome the limitation of accurate mathematical model and poor robust performance of conventional methods，a new design approach of adaptive flight control system for aircraft with center of gravity variations was proposed.The base control law was designed based on inverse dynamics and center of gravity estimation.Then the adaptive sliding mode control module was introduced，in which the sliding mode control could guarantee the robustness and stability of closed loop system，and the adaptive module was designed to compensate model uncertainties and estimation error.The stability of closed loop was proved using Lyapunov stability theory.Simulation results demonstrate that the proposed method compensates uncertainties effectively，and its robust performance is also excellent.

flight control systems;adaptive control systems;sliding mode control;center of gravity

V 249

A

1001-5965（2012）03-0314-05

2010-11-24;< class="emphasis_bold">网络出版时间:

时间:2012-03-20 10:37

www.cnki.net/kcms/detail/11.2625.V.20120320.1037.002.html

张 晶（1982－），女，河北保定人，博士生，jijizhj1982@163.com.

（编 辑:刘登敏）