星间DOWRT中的相对论效应分析与修正

孙文超 常 青 徐 勇 齐 巍

（北京航空航天大学 电子信息工程学院，北京 100191）

星间DOWRT中的相对论效应分析与修正

孙文超 常 青 徐 勇 齐 巍

（北京航空航天大学 电子信息工程学院，北京 100191）

推导了双向单程测距与时间同步（DOWRT，Dual One-Way Ranging/Time Synchronization）的解耦方程，分析了空间动态下DOWRT法的计算方法及相对论效应在测距和时间比对中的影响，提出了带有相对论效应修正的DOWRT算法，最后分别仿真分析了低轨编队飞行卫星和导航星座中的距离与时间同步测量中相对论效应引起的误差.结果表明:卫星间采用DOWRT测量方法时，由相对论效应引起的低轨短基线编队飞行卫星间距离测量误差为米级、时间同步误差为亚皮秒级，而在导航星座测量中引起近百米级距离测量误差和高达微秒级的时间同步误差.因此为了实现导航卫星间高精度距离与时间同步测量，必须进行相对论效应修正.

双向单程测距与时间同步;卫星导航星座;星间链路;误差分析;广义相对论

卫星编队飞行是近年来兴起并受到国内外航天界普遍关注的一个新的研究领域，而编队卫星间的距离和时间同步测量技术是其中一项关键技术，很多文献讨论了这一问题［1－5］.考虑到卫星运动的影响，文献［3］对双向法进行了修正，提出通过预先估计卫星的径向速度、星间距离实现动态下卫星距离和钟差的精确测量.

在全球导航定位系统中，星间链路的测量在辅助地面进行精密定轨、增加星历注入频度、增强星座自主运行和管理等方面起着重要作用.目前，美国GPS BLOCK-IIR卫星已具备了星间相对测量的能力［4］，一旦有足够的卫星在轨，GPS星座将可以实现战时的自主运行，但其星间链路的测量技术细节却很少公布，很多技术尚不清楚实现方法.所以针对导航星座的星间链路测量技术的研究与探索在建设我国全球卫星导航系统过程中有着重要的实际和战略意义.文献［5］介绍了一种导航卫星动态双向时间同步算法，提出利用星间伪距拟合多项式和钟差拟合多项式联合求解高精度星间钟差.

在大尺度空间范围内，以欧几里德空间为基础的经典牛顿力学理论中时间观测精度在10－8以内［6］，远不能满足现代高精度测量的要求，所以必须在相对论框架下考虑卫星间距离和时间同步测量这一问题.对此国内外鲜有文献提及，本文给出了动态下带有相对论效应修正的星间距离测量与时间同步的解耦方程，并仿真分析了相对论效应对LEO（Low Earth Orbit）卫星编队飞行和导航星座中测距与时间同步测量的影响.

1 基于双向法的DOWRT原理

基于双向法的双向单程测距技术DOWR（Dual One-Way Ranging）是一种非相干扩频测距和时间比对方法［1－2］，在这种方法中，每颗卫星均安装有发射机和接收机，通过伪码和载波相位测量，各自得到观测伪距，通过交换伪距消除多种误差量，实现星间精密测距，时间同步.其基本原理可用图1说明.

卫星A（B）在其钟面时刻tAt（tBt）发射测距帧信号，在tAr（tBr）时刻接收到对方卫星测距帧信号.其他参数定义为:①ρA为A卫星接收B卫星信号处理解算出来的伪距（基本观测量，时间单位）;②ρB为B卫星接收A卫星处理解算出来的伪距（基本观测量，时间单位）;③τAB（τBA）为测距信号在A星与B星（B星与A星）的天线相位中心之间的几何传输时延;④Δt为A星与B星发射（接收）测距信号时两星之间的钟差;⑤τAt，τAr，τBt，τBr分别为A星发射设备和接收设备的时延与B星发射设备和接收设备的时延.分析过程中以测距信号传播时延关系来推导测距卫星天线相位中心之间的几何距离，当忽略各种测量误差时，显然有

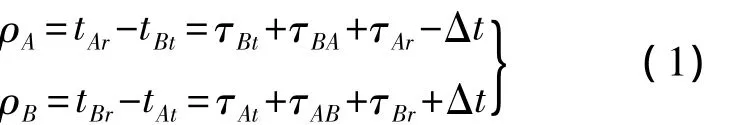
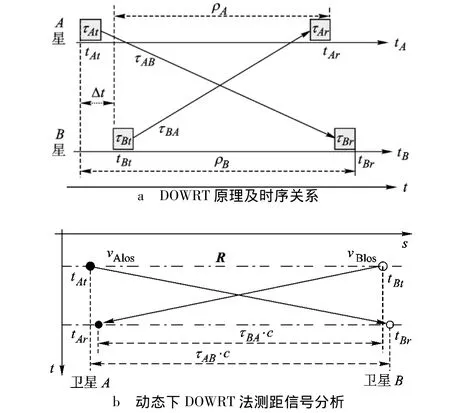
图1 DOWRT法的时空分析图

如图1b所示，由于卫星运动，测距信号在A星与B星（B星与A星）的天线相位中心之间的几何传输时延τAB（τBA）不同.R为信号发射时刻卫星A，B天线相位中心之间的几何距离矢量，vAlos，vBlos为卫星A，B速度在它们几何距离矢量上的投影，根据经典运动学原理有

由式（1）、式（2）可以得到经典理论下动态卫星间距离与时间同步测量的解耦方程:

2 DOWRT的广义相对论效应与修正

经典的牛顿理论认为同时性是瞬时的、绝对的，亦即惯性系中不同地点发生的事件都可以在一个时间轴上（用一只钟）给予记录.但是相对论理论认为（假设）:①光的传播速度不满足叠加性，光速恒定不变;②爱因斯坦同时性，即利用光信号将发生在不同地点的事件的时间维联系起来［6－8］.狭义相对论解决了相互做匀速运动的惯性系中时空度量的问题，广义相对论解决的是在任意惯性系之间时空度量的问题.经典理论中测量精度为10－8，不能满足高精度测量的要求.

在广义相对论中，时空坐标系是由与物质分布及引力场等有关的度规张量gαβ定义的，时空中四维不变弧元ds2表示如下［8］:

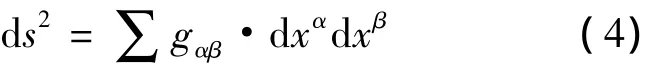
时空的测量与度规张量gαβ的选取有关，事实上，很难严格给出某一坐标系下度规的完整表达形式.

在地心非旋转坐标系下，采用1991年IAU第21次大会决议A4推荐的后牛顿精度近似下（c－2的精度对星间距离测量与时间同步而言已经足够）的时空度规:

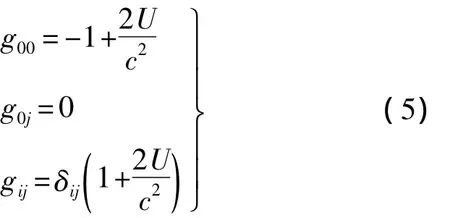
其中，U为地球的牛顿引力势和太阳等外部天体的引潮力之和;δij为科罗内克符号.

测距与时间同步的基础是测时，即前述问题的本质是对时间的计量.不同地点的时钟比对，除了与同时性的定义有关以外，还与信号的传播时延有关.式中的伪距观测值ρA，ρB就是接收卫星钟面时tAr（tBr）与发射卫星钟面时tBt（tAt）的比对（求差）.

在广义相对论框架下，形如式的通过无线电进行时间比对（求差）的问题，必须对相对论效应进行修正，即

其中，δBA（δAB）是测距信号由卫星A到卫星B（卫星B到卫星A）的相对论效应修正项，它们主要表现为引力时延.根据式（4）～式（6）且只考虑地心引力项，可以得出如下的表达式（皮秒量级）:

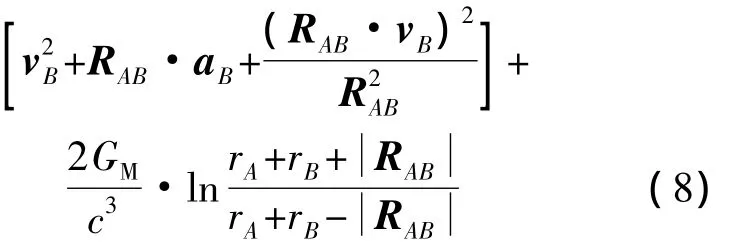
其中，RBA（RAB）表示由卫星B指向卫星A（卫星A指向卫星B）的几何距离矢量;vA（vB）和aA（aB）分别表示卫星A（B）在地心非旋转坐标系下的速度和加速度矢量;rA（rB）则表示卫星A（B）到地心的距离值;GM为地心引力常数.因为近似过程只考虑了地心引力影响，所以只有在地球附近2×105km的范围内式（7）、式（8）才有效.

式（7）、式（8）中，等号右边第1项，在地心地固坐标系中表现为Sagnac效应，在星间时钟比对中影响量级为102ns;第2项中卫星的加速度项的影响很小可以忽略.第3项为引力势项，并且有

而且根据图1有 RAB≈R，RBA≈－R，所以式（7）、式（8）可以近似表达为

需要说明的是，广义相对论框架中式中的τBA，τAB称为几何时延，且有

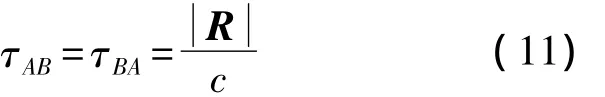
这样结合式（6）、式（10）、式（11）就可以得到动态下进行了相对论效应修正（后牛顿精度下）的卫星间测距与时间同步解耦方程:

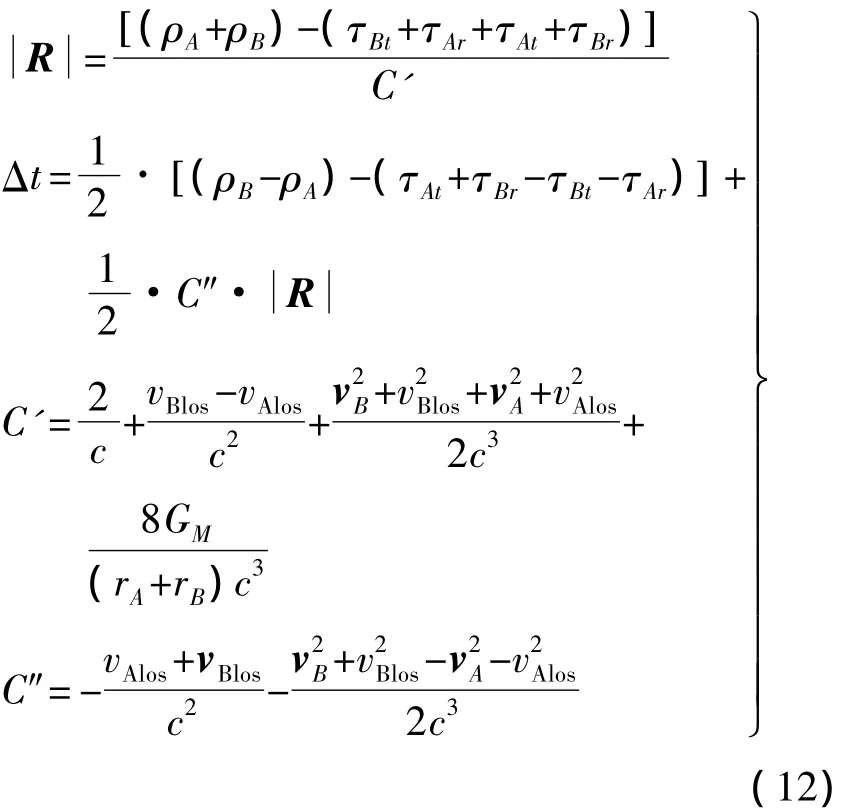
3 数值仿真分析

文献［9］给出了相对论效应对卫星时钟的影响.表1中摘录了4种卫星的相对论效应中影响量级较大的Sagnac效应典型值.其中第3行给出按式（7）、式（8）中等式右边第1项计算的Sagnac效应值.可见通过式（7）、式（8）计算的Sagnac效应值与典型值基本吻合.

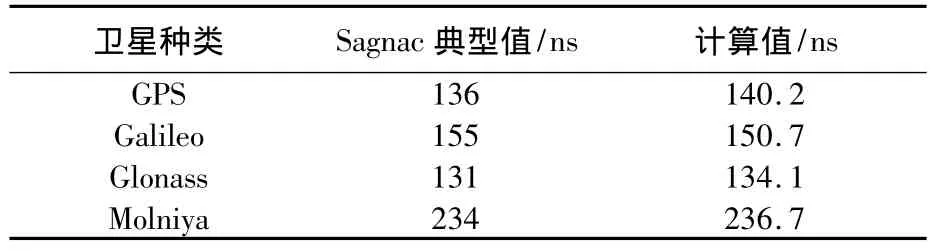
表1 Sagnac效应典型值与计算值比较

下面通过仿真对比分析LEO卫星编队间和导航星座卫星间DOWRT法测量中的相对论效应引起的误差.假设 LEO卫星编队轨道高度约240 km，基线长度约370 km;导航星座由24颗MEO（Medium Earth Orbit）卫星（Walker24/3/2）、3颗GEO（Geostationary Earth Orbit）卫星和3颗IGSO（Inclined Geosynchronous Orbit）卫星组成，其中MEO卫星轨道高度为24126km，GEO/IGSO卫星轨道高度35 780 km.并忽略接收机测量误差、原子钟变化误差、测量设备延时误差、天线相位中心的偏差.

图2、图3为LEO卫星编队间和导航星座中MEO卫星间DOWRT法中相对论效应引起的误差.结果表明:对低轨短基线编队飞行的卫星而言，相对论效应对DOWRT法测量的影响较小（距离测量误差为米级、时间同步误差为亚纳皮级），而在导航星座中MEO卫星间的距离测量误差为百米级、（异轨中）时间同步误差为微秒级.可见，卫星的轨道高度和星间的相对距离决定着相对论效应误差的量级.

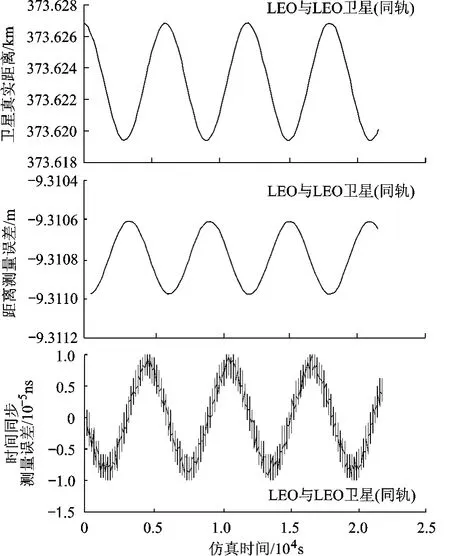
图2 LEO卫星编队星间测量相对论效应误差

图4为导航星座中MEO与GEO（IGSO）卫星测量的相对论效应误差分析.由图可知，相对论效应对不同轨道高度卫星MEO与GEO（IGSO）卫星间的距离测量引起百米量级的误差，引起的时间同步测量误差为微秒量级.

图4 导航星座中MEO与GEO（IGSO）卫星间测量的相对论效应误差

4 结论

本文通过研究与分析相对论效应对DOWRT法测量的影响，得到了以下结论:①相对论效应引起的误差与测距卫星相对距离和在此距离方向上的速度投影有关;②卫星的轨道高度和星间相对距离决定了相对论效应引起的误差量级;③相对论效应对短基线LEO卫星编队距离测量产生的误差为米级、时间同步误差为亚皮秒级，但在导航星座中，相对论效应引起的距离测量误差为百米级、时间同步误差为微秒级.

综上，为实现导航星座卫星间的高精度DOWRT，必须考虑相对论效应的影响，并按修正公式进行解耦计算.

（References）

［1］李雪，张其善，徐勇，等.AFF组网通信与测距/时间同步的新体制研究［J］.通信学报，2008，29（5）:81－87

Li Xue，Zhang Qishan，Xu Yong，et al.New techniques of intrasatellite communication and ranging/time synchronization for autonomous formation flyer［J］.Journal on Communications，2008，29（5）:81－87（in Chinese）

［2］Jeongrae Kim.Measurement time synchronization for a satelliteto-satellite ranging system［C］//International Conference on Control，Automation and Systems.Seoul，Korea:［s.n.］，2007:190－194

［3］钟兴旺，陈豪.卫星运动对星间双向法时间同步的影响分析与校正［J］.中国空间科学技术，2007，6（12）:54－58

Zhong Xingwang，Chen Hao.Analysis and correction techniques of movement influence on inter-satellite two-waytime transfer［J］.Chinese Space Science and Technoigy，2007，6（12）:54－58（in Chinese）

［4］Ananda M P，Bernstein H，Cunningham K E，et al.Global positioning system（GPS）autonomous navigatio［C］//Position Location and Navigation Symposium，1990.Record.The 1990's-A Decade of Excellence in the Navigation Sciences.Las Vegas，NV，USA:［s.n.］，1990:497－508

［5］黄飞江，卢晓春，吴海涛，等.基于星间距离变化的动态双向时间同步算法［J］.武汉大学学报:信息科学版，2010，1（1）:13－16

Huang Feijiang，Lu Xiaochuan，Wu Haitao，et al.An algorithm of dynamic two-way time transfer based on inter-satellite range variation［J］.Geomatics and Information Science of Wuhan University，2010，1（1）:13－16（in Chinese）

［6］刘利.相对论时间比对理论与高精度时间同步技术［D］.郑州:解放军信息工程大学测绘学院，2004

Liu Li.Relativistic theory of time transfer and techniques of clock synchronization［D］.Zhengzhou:School of Geodesy and Geomatics，The PLA Information Engineering University，2004（in Chinese）

［7］韩春好.相对论框架中的时间计量［J］.天文学进展，2002，20（6）:107－112

Han Chunhao.Time measurement within the framework of relativity［J］.Progress in Astronomy，2002，20（6）:107 －112（in Chinese）

［8］Gernot M R Winkler.Synchronization and relativity［J］.Proceedings of the IEEE，1991，79（6）:1029－1039

［9］Francis S，Stein S，Celano T，et al.Analytical tools for clock in space［C］//Proceedings of the 2003 IEEE International Frequency Control Symposium and PDA Exhibition/Jointly with the 17 th European Frequency and Time Forum.Tampa，Florida USA:IEEE，2003:312－316

Analysis and correction on relativistic effect of inter-satellites using dual one-way ranging/time synchronization

Sun Wenchao Chang Qing Xu Yong Qi Wei
（School of Electronics and Information Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

The calculation of dual one-way ranging/time synchronization（DOWRT）between dynamic satellites was analyzed.In addition，relativistic effect on ranging/time synchronization was presented.A calculation with relativistic correction of DOWRT was proposed.Measurement errors of ranging/time synchronization in low earth orbit（LEO）formation constellation and in navigation constellation caused by relativistic effect were simulated and comparatively analyzed.Simulation results demonstrate that when inter-satellite DOWRT method is adopted，ranging measurement and time synchronization errors during LEO formation flying caused by relativistic effects are in meter-scale and sub-picosecond level respectively，while in navigation constellation measurement，the corresponding errors would be in hundred-meter scale and microsecond level.As a result，relativistic correction should be included in order to realize high-precision ranging and time synchronization measurement between navigation satellites.

dual one-way ranging/time synchronization（DOWRT）;navigation constellation;inter-satellite links;error analysis;general relativity

TN 927;TN 961

A

1001-5965（2012）03-0335-05

2010-11-30;< class="emphasis_bold">网络出版时间:

时间:2012-03-09 10:37

www.cnki.net/kcms/detail/11.2625.V.20120309.1037.017.html

国家自然科学基金资助项目（60872062）;国家高技术研究发展计划（“863”计划）资助项目（2007AA12Z336，2009AA12Z313）;航天科技重点创新基金资助项目（2009-06）

孙文超（1986－），男，天津人，硕士生，wenchao35092207@yahoo.com.cn.

（编 辑:娄 嘉）