降低PLC系统峰均比的低复杂度改进SLM算法

陈 可 胡晓光

（北京航空航天大学 自动化科学与电气工程学院，北京 100191）

降低PLC系统峰均比的低复杂度改进SLM算法

陈 可 胡晓光

（北京航空航天大学 自动化科学与电气工程学院，北京 100191）

针对信道慢时变特性及噪声复杂的特点，提出了适用于低压电力线通信的降低峰均比的改进算法.改进算法对原始输入序列中的部分数据进行循环移位来获得一系列不同的新数据序列;在每个新数据序列尾部插入相应的边带信息组成一个输入候选序列;对这一系列不同的输入候选序列分别实施傅里叶反变换，得到不同的输出序列;从中选择峰均比最小的用于传输，达到降低系统峰均比的目的.结果表明:改进算法能够有效地降低系统的峰均比，并且能够获得更好的误码率性能，同时具有比传统选择性映射方法更低的计算复杂度.

电力线通信;正交频分复用;峰值平均功率比;选择性映射;误码率

大量实际测量结果表明，低压配电网一方面具有噪声干扰强、线路衰减大、多径传输和频率选择性衰落严重的特点;另一方面，由于电网上负载的不断接入、切出，电器有开有关等各种随机事件，使得低压电力线拓扑结构复杂［1］，而正交频分复用（OFDM，Orthogonal Frequency Division Multiplexing）技术具有抗多径时延、抗频率选择性衰落、传输速率高、频带利用率高、均衡技术简单等优点［2］，因此，OFDM成为目前低压电力线通信研究热点之一.尽管OFDM技术有许多优点，但与单载波系统相比，由于OFDM符号是由多个独立的经过调制的子载波信号相加而成，不同的子载波在相位和时间上线性叠加，这样的合成信号就有可能产生较大的峰值功率，由此会带来较大的峰值平均功率比（PAPR，Peak－to－Average Power Ratio）［3］，它直接影响着整个系统的运行效率.因此，必须降低信号的PAPR，使发射机中的功率放大器高效工作，提高系统的整体性能.

近年来国内外学者提出了许多有效地降低PAPR的方法，包括限幅、峰值加窗、校正函数、压缩扩张、格雷互补序列、雷德密勒码、分组编码、选择性映射［4－7］（SLM，Selected Mapping）和部分传输序列等方法.其中，SLM是一种非常有效的降低系统PAPR的方法，该方法可有效降低信号的PAPR，不会引起信号的失真，适用于任意数目的子载波和任意的调制方式，且只引起很小的数据速率损失，缺点是需要将多个相位旋转因子分别与傅里叶反变换（IFFT，Inverse Fast Fourier Transform）的输入序列进行点乘运算，增加了系统的运算复杂度，而且为了使接收端准确地恢复发送端的信息，发送端需要利用额外的子信道发送边带信息（SI，Side Information）.为了克服SLM方法的缺点，文献［6］提出了一种伪序列插入方法，主要包括方法 1（M1，Method 1）、方法 2（M2，Method 2）、方法3（M3，Method 3），这3种方法均是在发送序列后插入不同的伪序列，如:互补序列和其他类型的伪序列来扰乱发送序列，以此改变发送序列的相关特性，达到降低系统PAPR和复杂度的目的.本文所提出的改进方法也将和M1方法、M2方法、M3方法作对比.

本文在对传统SLM方法研究基础上，提出了一种部分数据循环移位的算法，通过循环移位的方式扰乱发送序列，达到降低系统峰均比的目的，该算法省去了旋转向量的点乘运算，降低了系统的计算复杂度.

1 低压电力线信道特性及模型

根据文献［2］可知，电力线信道主要是具有频率选择性衰减特性的多径信道，采用“由上而下”的建模方法，将信道看作一个黑盒，模型的相关参数从实地的测量数据中获取，考虑的信号频率范围从1～20 MHz，对低压电力线信道建模，用频率响应函数表示为

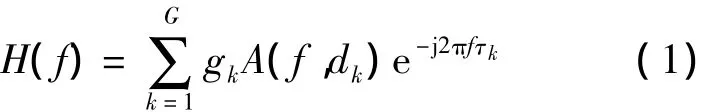
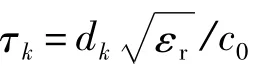
低压电力线上存在多种噪声［1］，主要有:①有色背景噪声;②窄带噪声;③与工频同步的周期性噪声;④与工频异步的周期性噪声;⑤异步冲激噪声.其中，噪声①和②随时间变化缓慢，可将其总和看作总的背景噪声;噪声③主要集中在较低频段（＜1 MHz）;噪声④和⑤影响信道的时间很短，故本文主要考虑背景噪声对系统的影响.低压电力线信道上的背景噪声一般为非高斯分布，对于OFDM通信系统，非高斯噪声对系统性能的影响可等效为高斯噪声的影响.因此，本文采用式（1）作为低压电力线多径信道模型，采用高斯噪声作为电力线信道噪声模型.

2 系统模型及PAPR定义

基于OFDM技术的电力线载波通信系统方框图如图1所示.

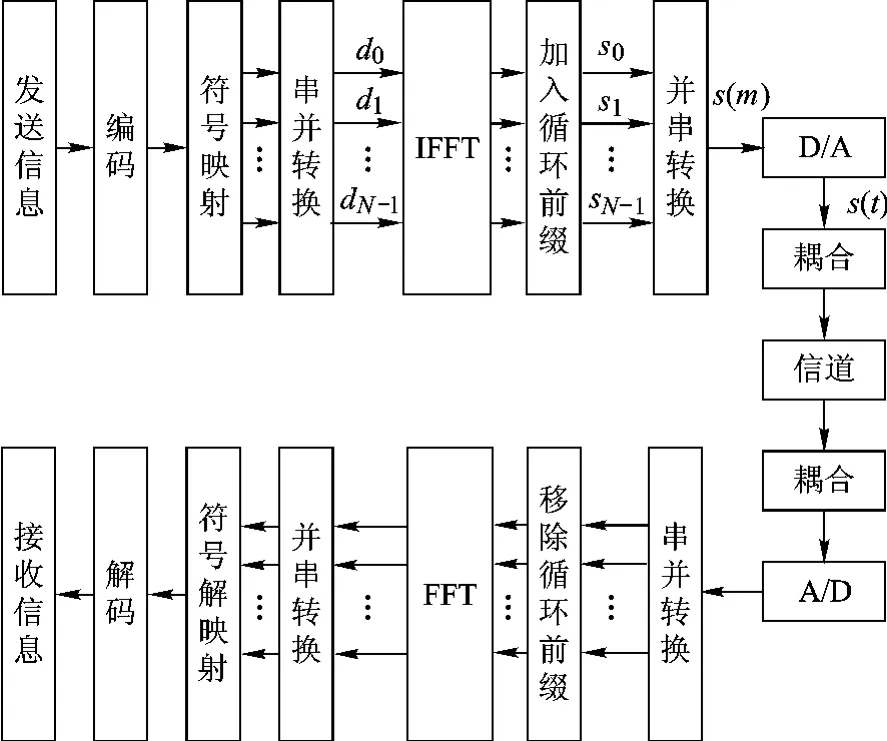
图1 基于OFDM技术的电力线载波通信系统方框图

发送信息经过编码后将比特流映射到符号上，通常采用的映射方式有二进制相移键控（BPSK，Binary Phase Shift Keying）、四相相移键控（QPSK，Quadrature Phase Shift Keying）等，映射后的符号流经过串并转换器，将串行数据流转换为N（N为子载波个数）路并行数据，N路并行数据流经过IFFT模块后分别调制到N路并行的子载波上，再计算出IFFT样值，在样值前加上一个循环前缀，就形成了一个循环拓展的OFDM信息码字.循环拓展信息码的样值再依次经过并串转换、数/模转换、低通滤波、功率放大后，通过耦合电路耦合到电力线上.接收端完成了与发送端相反的操作，实现对发送数据的恢复.

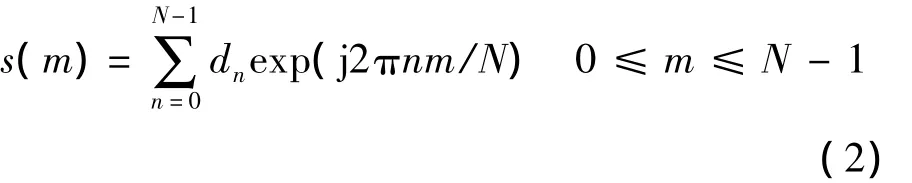
对于包含N个子载波的OFDM系统，在一个符号时间间隔内，经过IFFT变换后的输出信号可以表示为式中，n为子载波序号;dn为由二进制输入信号经过串并转换后得到的频域子载波信号;m为采样值序号.

输出信号经过数/模转换和低通滤波器后得到连续时间复基带信号可以表示为

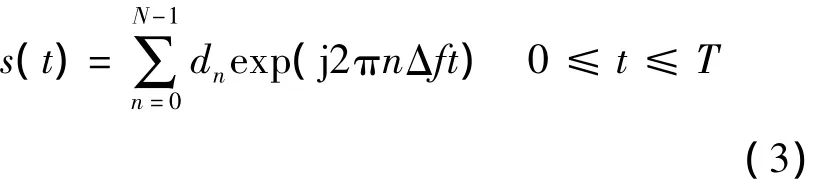
式中，Δf为子载波频率间隔;T为OFDM符号周期;t为时间.

峰值平均功率比为:一个OFDM信号的峰值功率与其平均功率的比值，表示为

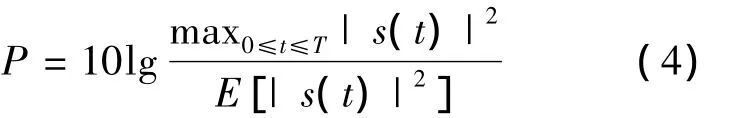
式中，P为峰值平均功率比;s（t）为连续时间信号;max（z）表示z的最大值;E［u］表示u的数学期望.

3 改进算法

改进算法的OFDM系统发送端方框图如图2所示.图中，IFFT分支的数量是U，边带信息S（i）记录循环移位的次数，表示为

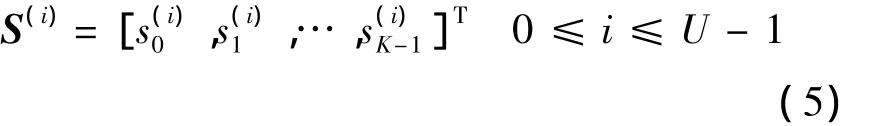
式中，［·］T表示转置操作;s为移位次数;i为IFFT分支序号;K为边带信息的长度.

输入数据序列D表示为

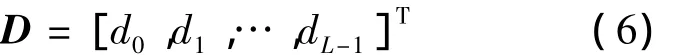
式中，d为输入数据序列中的数据位;L为数据序列总长度.

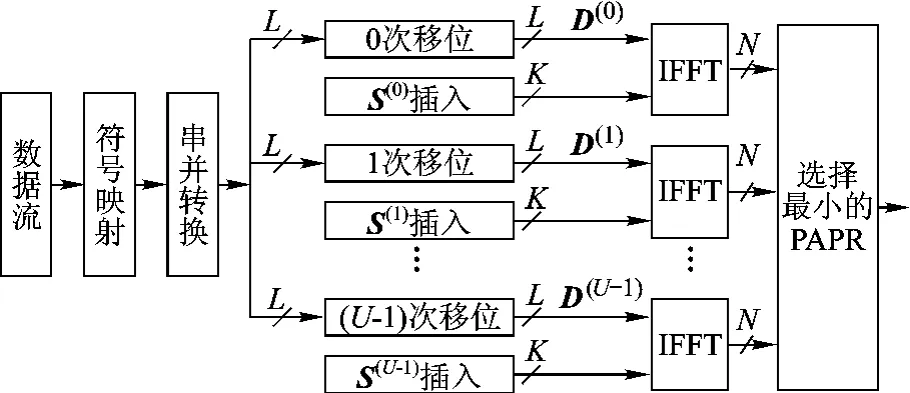
图2 改进算法方框图

改进算法对IFFT的原始输入序列中的部分数据进行循环移位来获得一系列不同的新数据序列，在每个新数据序列尾部分别插入相应的边带信息组成一个输入候选序列，对这一系列不同的输入候选序列分别实施IFFT运算，得到不同的输出序列，再从不同的输出序列中选择PAPR最小的用于传输，以达到降低OFDM系统PAPR的目的.假定有10个输入数据，则

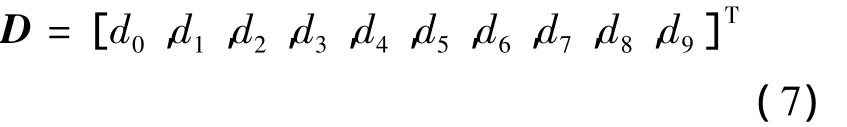
每次循环移位的数据位部分假定为:d2，d3，d4，d5，d6，d7.原始数据序列经过第 i次循环移位后的新数据序列记为D（i），则经过第1次循环移位后的新数据序列为

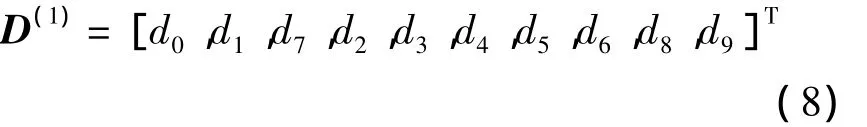
经过第2次循环移位后的新数据序列为

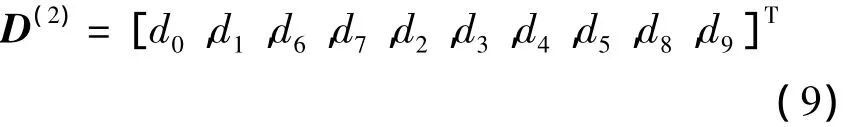
相应的边带信息S（i）被插入到D（i）的尾部，组成一个完整的IFFT输入序列.经过IFFT变换之后，形成U个候选OFDM符号，从U个候选OFDM符号中选择PAPR最小的一个符号传输，从而达到降低PAPR的目的.

对于传统SLM方法，边带信息需要利用额外的子信道传输，所以需要占用OFDM系统的部分带宽，然而，改进算法中，边带信息被附加在发送信号之后，在接收端，利用边带信息能够获取循环移位的次数，再将接收到的数据向相反的方向循环移位，从而恢复发送端的数据信息.此外，与传统SLM方法相比，改进算法并不需要相位旋转所带来的乘法运算，降低了计算复杂度.

在改进算法中，通过循环移位的方式来扰乱IFFT输入数据序列中的部分数据位，再将相应的边带信息插入到新的数据序列之后形成一个输入候选序列，输入候选序列结构图如图3所示.

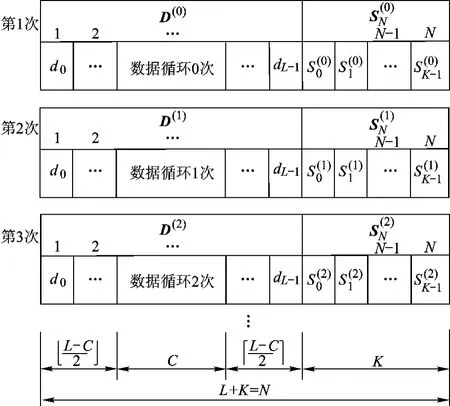
图3 改进算法输入候选序列结构图

式（6）还可以表示为

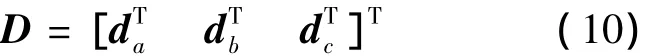
式中，da=［d0，d1，…，dw－1］T为 D 的前半部分，w=⎿（L－C）/2」为da的数据长度，C为数据序列中移位部分长度，⎿x」表示不大于x的最大整数;db=［dw，dw+1，…，dw+C－1］T为 D 中循环移位部分;dc=［dw+C，dw+C+1，…，dL－1］T为 D 的后半部分.

任意两个IFFT分支的互相关函数可表示为

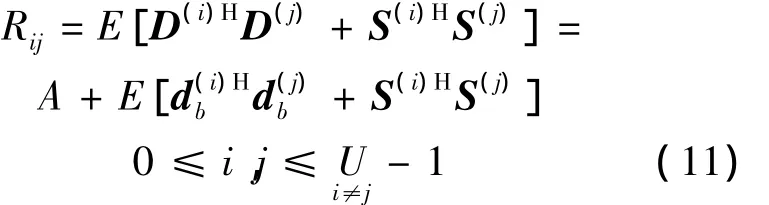
式中，［·］H表示共轭转置;A为一定值.

在（11）式中，由于da和dc是固定不变的，Rij的值由db和S决定，对于不同的db和S，Rij的值是不同的，因此 PAPR值不同，从这些不同的PAPR值中选择最小的一个用于传输，从而能够降低系统的PAPR.同时，误码率的性能也依赖于db和S，如果C比较大，当边带信息在接收的过程中发生错误时将导致系统的误比特数增加，为了选择一个最优的C值，将C定义为

式中，α∈{0，0.1，0.2，…，1}为移位长度因子.通过选择不同的α值，可得到不同的C值.

4 仿真系统及信道参数设置

仿真中信道噪声用高斯白噪声模拟，基于低压电力线的OFDM系统子载波数量N为64.调制方式分别采用QPSK与BPSK方式，L，K满足L+K=24.SLM 方法、M1 方法、M2 方法、M3 方法、改进算法的边带信息长度 K 分别为 0，4，4，4，4，相应的 IFFT 长度 U 分别为16，4，16，16，16，每次仿真的OFDM符号个数为10000个.

调制频带1～20 MHz.根据低压电力线信道特性，仿真系统参数设置如表 1所示，CP为OFDM符号的循环前缀.

表1 系统参数

仿真 4 径信道，取 α0=0，α1=7.8×10－10s/m，h=1，εr=3.8，c0=3.0×108m/s，低压电力线信道参数如表2所示.

表2 信道参数

5 仿真结果与分析

通过仿真实验得出改进算法在PAPR增加的情况下互补累积分布函数（CCDF，Complementary Cumulative Density Function）的变化以及信噪比（SNR，Signal to Noise Ratio）增加的情况下误码率（BER，Bit Error Rate）的变化.

在图4中，分别采用BPSK与QPSK调制方式，边带信息的长度分别取K=4及K=5，仿真对于不同的移位长度α值，OFDM系统峰均比超过6 dB的概率曲线.

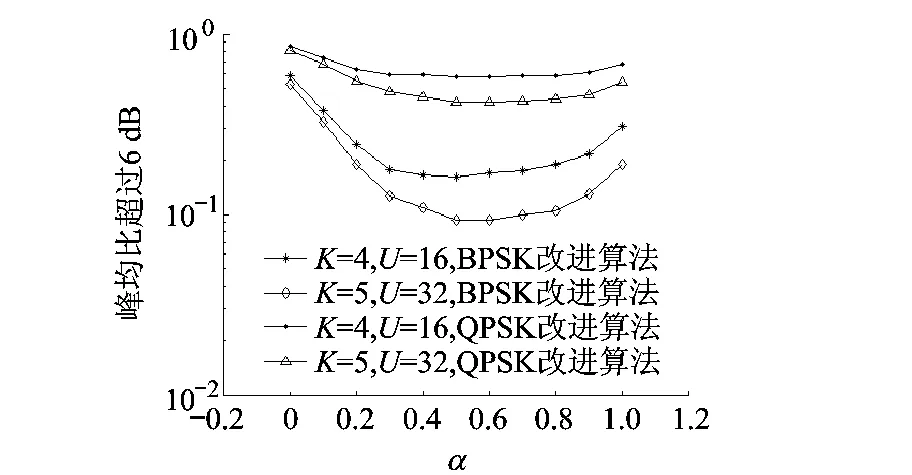
图4 移位长度与峰均比超过6 dB的关系图

从图4中可以得出结论:当α在0～0.5之间变化时，曲线变化比较明显，随着α值的增大，PAPR超过6 dB的概率逐渐减小;当α在0.5～0.7之间变化时，曲线变化趋于平稳，PAPR超过6 dB的概率大致相同，此时PAPR超过6 dB的概率达到最小;当α在0.7～1.0之间变化时，曲线变化也比较明显，随着α值的增大，PAPR超过6 dB的概率逐渐增大.此外，循环移位的数据长度越短，误码率的性能将会更优.因此，在降低PAPR与误码率性能之间折衷考虑，选择α=0.6，并将此值作为后面仿真时计算数据循环移位长度的依据.

图5所示是采用QPSK调制方式，原始信号、SLM方法、M1方法、M2方法、M3方法以及改进算法的互补累积分布函数曲线.

从图5中可看出，SLM方法、M1方法、M2方法、M3方法以及改进算法均改善了OFDM系统的PAPR性能.在CCDF=0.1%时，原始信号、M3方法、M1方法、M2方法、改进算法以及SLM方法的 PAPR 分别为 10.5，10.4，10.1，9.6，8.3，7.1 dB.虽然改进算法在改善OFDM系统PAPR性能方面略差于SLM方法，但与原始信号、M3方法、M1方法、M2方法相比，在改善 OFDM系统PAPR 性能方面有了2.2，2.1，1.8，1.3dB 的提高.

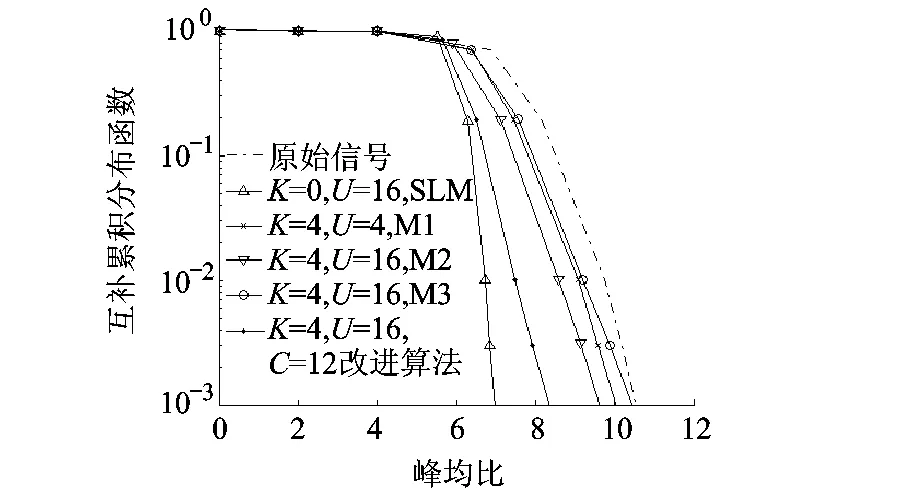
图5 峰均比性能曲线

图6所示是采用QPSK调制方式，原始信号、SLM方法、M1方法、M2方法、M3方法以及改进算法的误码率曲线.

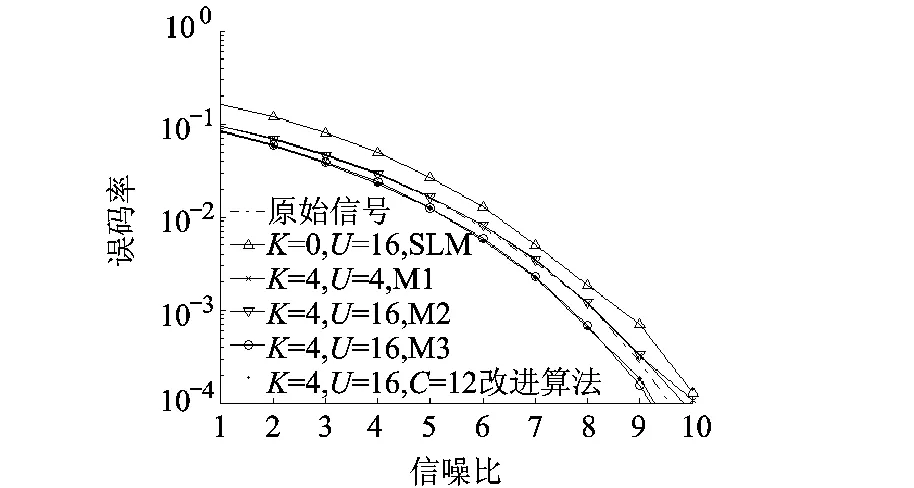
图6 误码率性能曲线

从图6中可以看出，当K=4时，改进算法与M3方法的误码率曲线基本重合，这两种方法均优于M1方法、M2方法、原始信号以及SLM方法.在BER=0.01%时，改进算法、M3方法、原始信号、M2方法、M1方法以及SLM方法的信噪比分别为 9.2，9.3，9.5，9.7，9.8，10.4 dB.改进算法获得了最优的误码率性能，与SLM方法相比，信噪比有了1.2dB的提高，原因是SLM方法需要占用大量额外的信道来传输相位旋转信息，当传输信息的子信道受到干扰，接收端将无法准确地对发送端信号进行恢复，从而产生较大的误码率，在改进算法中，边带信息被附加在传输信号后，占用的子载波个数较少，且改进算法是采用循环移位方式来降低PAPR，即使某个子信道受到干扰也不会对整个系统的误码率性能产生较大影响.

图7所示是采用BPSK调制方式，原始信号、SLM方法、M1方法、M2方法、M3方法以及改进算法的误码率曲线.

将图7与图6对比可以看出，采用BPSK调制方式的误码率性能比采用QPSK调制方式的误码率性能要好.因为信道和噪声即使对信号的幅度和相位产生影响，只要相位产生的偏差不超过±π/2，对BPSK解调来说都不会产生误码，当采用QPSK调制时，若在星座图上相位偏移超过±π/4就会产生误码.当采用BPSK调制，一个信号调制一个比特位，若采用QPSK调制，一个信号调制两个比特位，所以QPSK比BPSK传输速率提高一倍.

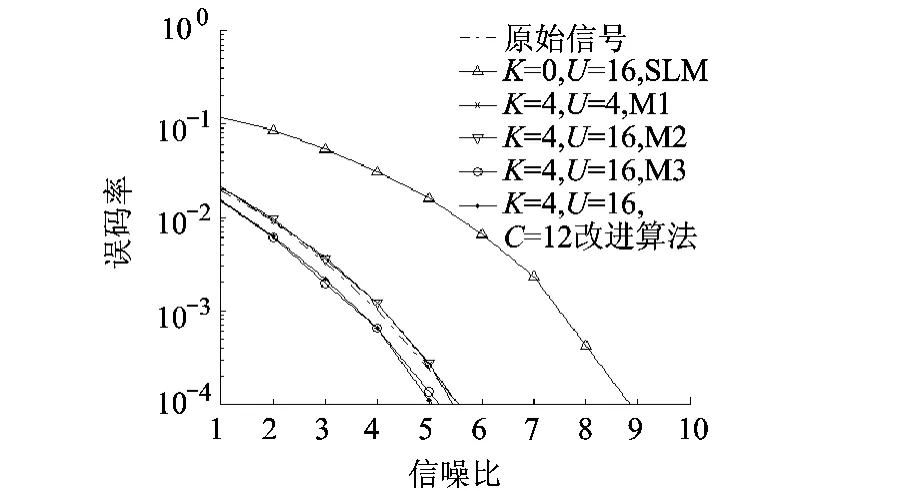
图7 误码率性能曲线

图8所示是采用QPSK调制方式，仿真了多径传输信道与高斯白噪声下的原始信号、SLM方法、M1方法、M2方法、M3方法以及改进算法的误码率曲线.从图8可以看出，改进算法与M3方法的误码率曲线基本重合，这两种方法均优于M1方法、M2方法、原始信号以及SLM方法.将图8与图6对比可以看出，在相同的信噪比下，采用多径信道加白噪声时误码率性能比只采用白噪声时的误码率性能有所下降，原因是仿真中采用的多径信道模型具有频率选择性衰落特性，随着频率的增加，衰减增加，并且多径时延造成了数据符号之间相互重叠，产生码元之间的串扰，导致误码率性能下降.

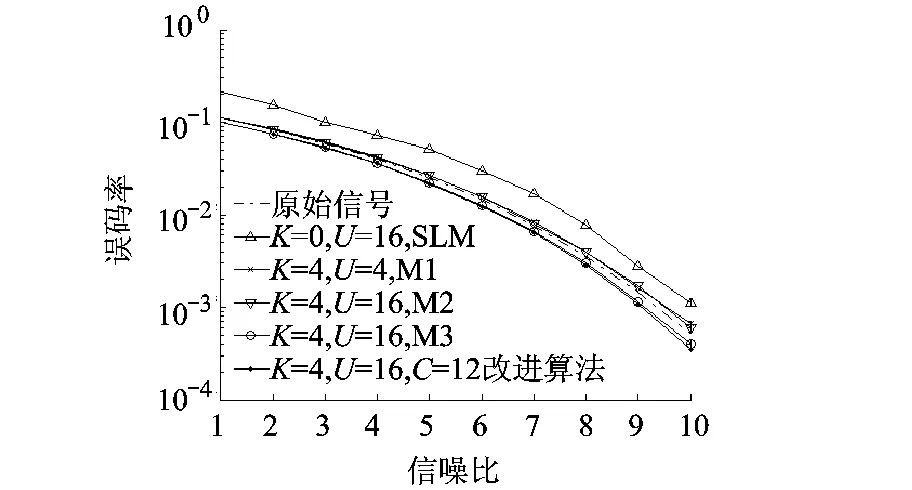
图8 误码率性能曲线

表3和表4分别列出了SLM方法、M1方法、M2方法、M3方法以及改进算法在发送端和接收端的计算复杂度.从表3和表4可以看出，改进算法的计算复杂度和M1方法、M2方法、M3方法相当，均比SLM方法计算复杂度要低，因为改进的算法是通过数据循环移位的方式降低系统的PAPR，而SLM方法是通过相位旋转的方式降低系统的PAPR，微处理器实现相位旋转所需的乘除法运算远比实现循环移位运算复杂.

表3 发送端的计算复杂度

表4 接收端的计算复杂度

6 结论

针对低压电力线通信信道的特点，本文在传统SLM方法的基础上，提出了利用部分数据循环移位的方式降低OFDM系统中的PAPR，仿真结果表明:在改善系统PAPR性能方面，改进算法比SLM方法效果稍差，但优于文献［6］中的伪序列插入方法;在改善误码率性能和系统计算复杂度方面，改进的算法均优于SLM方法.虽然改进算法在降低计算复杂度和误码率方面优于传统SLM算法，但在降低系统PAPR方面性能略差，这也是今后研究工作的重点.

（References）

［1］唐良瑞，张勤，张平.正交频分复用系统中基于迭代插值的低压电力线信道估计［J］.中国电机工程学报，2010，30（1）:98－102

Tang Liangrui，Zhang Qin，Zhang Ping.Channel estimation based on iterative interpolation for low－voltage power line in orthogonal frequency division multiplexing system［J］.Proceedings of the CSEE，2010，30（1）:98－102（in Chinese）

［2］王东.OFDM在低压电力线载波系统中的仿真与应用［D］.成都:电子科技大学自动化科学与电气工程学院，2008

Wang Dong.OFDM simulation and application in low voltage power line carrier system［D］.Chengdu:School of Automation Science and Electrical Engineering，University of Electronic Science and Technology，2008（in Chinese）

［3］孙宇明，张彦仲，邵定蓉，等.OFDM系统定时偏差补偿算法［J］.北京航空航天大学学报，2010，36（6）:728－731

Sun Yuming，Zhan Yanzhong，Shao Dingrong，et al.Timing offset compensation algorithm for OFDM system［J］.Journal of Beijing University of Aeronautics and Astronautics，2010，36（6）:728－731（in Chinese）

［4］Li Chihpeng，Wang Senhung，Wang Chinliang.Novel low－complexity SLM schemes for PAPR reduction in OFDM systems［J］.IEEE Transactions on Signal Processing，2010，58（5）:2916－2921

［5］Wang Chinliang，Ku Shengju，Yang Chunju.A low complexity PAPR estimation scheme for OFDM signals and Its application to SLM－based PAPR reduction［J］.IEEE Journal of Selected Topics in Signal Processing，2010，4（3）:637－645

［6］Sang Wookim，Heui Seopbyeon，Jin Kwankim，et al.An SLM－based real－time PAPR reduction method using dummy sequence insertion in the OFDM communication［C］//Han S H.Communications and Signal Processing.Thailand:Bangkok，2005:258－262

［7］Byung Moo Lee，Rui J P de Figueiredo.MIMO－OFDM PAPR reduction by selected mapping using side information power allocation［J］.Digital Signal Processing，2010，20（2）:462－471

Low complexity improved SLM algorithm for PAPR reduction in PLC system

Chen Ke Hu Xiaoguang

（School of Automation Science and Electrical Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

A reduce peak－to－average power ratio（PAPR）algorithm was proposed aim at the slow－variant and complex noise of channel.The partial data within the original data sequence were scrambled by circularly shifting to obtain a set of new data sequences.Each new data sequence tail was inserted the corresponding side information（SI）to form the input candidate sequence.Inverse fast Fourier transform（IFFT）was operated by different input candidate sequence separately to obtain different output sequence.Chosen of the lowest PAPR，the PAPR of system could be greatly reduced.The simulation results indicate that the improved algorithm can reduce PAPR effectively and get a better bit error rate and the algorithm has lower computational complexity than selected mapping（SLM）.

power line communication;orthogonal frequency division multiplexing;peak－to－average power ratio;selected mapping;bit error rate

TN 914.66

A

1001－5965（2012）03－0394－06

2010－12－29;< class="emphasis_bold">网络出版时间:

时间:2012－03－20 10:37

www.cnki.net/kcms/detail/11.2625.V.20120320.1037.009.html

北京航空航天大学青年教师创新基金资助项目（911901340）

陈 可（1981－），男，江西九江人，博士生，coco_chen81925@yahoo.com.cn.

（编 辑:赵海容）