自由边界抛物薄壳的模态振型函数

王新杰 岳洪浩 邓宗全

（哈尔滨工业大学 机电工程学院，哈尔滨 150001）

自由边界抛物薄壳的模态振型函数

王新杰 岳洪浩 邓宗全

（哈尔滨工业大学 机电工程学院，哈尔滨 150001）

基于membrane理论，推导出一组完全满足抛物薄壳自由边界条件的模态振型函数.通过模态分析实验得到自由边界抛物薄壳的低阶模态实验振型，将实验振型与有限元分析振型及依据模态振型函数所得到的理论振型进行对比，三者能够较好的吻合，表明所推导的模态振型函数可正确描述抛物薄壳的模态形状.

抛物薄壳;模态振型函数;membrane理论;模态分析

抛物壳结构具有聚焦特性和良好的空气动力学性能，在航空航天领域得到广泛的应用，如大型薄壁通信天线、太空光学反射镜和火箭整流罩等.而抛物壳结构的振动抑制问题，成为工程应用和设计中的难点和重点.近年来众多学者通过智能材料对抛物壳结构进行主动振动控制从而达到抑制振动的目的［1－2］.而抛物壳结构的模态振型反映了结构对外载荷响应的相对幅度、相位和振动形状，是研究板壳结构智能监测、传感/作动器设计与布局的重要依据和基础.

针对抛物壳的动力学问题的研究起步较早，众多学者作了大量的研究工作［3－9］，但针对抛物壳模态振型所开展的研究则相对较少.1960年，Lin和Lee推导了基于弯矩假设的自由边界条件下的模态形状方程［10］，但实际上该模态形状方程只满足弯矩假设条件而并不满足自由边界条件.1964年，Hoppmann等人采用实验的方法描绘出不同边界条件下抛物壳的振动节线［11］.1973年，Glockner和Tawadros对抛物壳在简支和固支条件下的自由振动进行了实验，并给出抛物壳模态形状的离散实验值［12］.2005 年，Kang和 Leissa应用三维Ritz方法分析了不同厚度抛物壳弹性结构的自由振动特性，利用包含有厚度参数在内的多项式来表示抛物壳的模态形状函数，但并没有给出抛物壳在相应边界条件下模态形状函数的具体形式［13］.综上所述，针对自由边界抛物壳的模态振型函数仍需进一步的理论研究，开展对应的模态实验分析，进行验证非常有必要.

本文以自由边界抛物薄壳的模态振型为研究对象.首先基于membrane简化，对自由边界条件下抛物薄壳的模态振型函数进行理论推导;然后通过模态分析实验，对所推导出的模态振型函数进行验证.

1 抛物壳的薄膜力与薄膜剪力

定义抛物壳的曲线正交坐标系为（φ，ψ，α3）.φ，ψ和α3分别表示抛物壳的子午线方向、圆周方向和横截方向，如图1所示.用c和a分别表示抛物壳的高度及开口半径;并引入参数b，且b=a2/（2c）.φ*表示子午线方向的边界弧度，且φ*=arctan（2c/a）.则子午线曲率半径 Rφ=b/cos3φ，圆周曲率半径Rψ=b/cosφ.

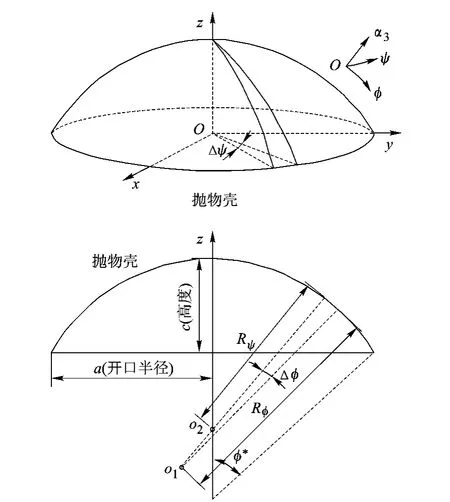
图1 抛物壳的曲线坐标系

设抛物壳中曲面在φ，ψ和α3方向的位移分量分别为uφ，uψ和u3，则抛物壳薄膜力、薄膜剪力与位移的关系可表示为［14］

2 自由边界抛物薄壳模态振型函数

当壳体的厚度与曲率半径的比值小于0.05时，可采用 membrane理论［15］，忽略壳体的弯矩、扭矩及横向剪力.本节将采用membrane理论对自由边界抛物薄壳的模态振型函数进行推导.

对于自由边界抛物壳，其边界上的所有力与力矩都应为零，由于本文采用了membrane理论，忽略了壳体的弯矩、扭矩及横向剪力，因此边界约束条件简化为边界上（即φ=φ*时）沿着子午线和圆周方向的薄膜力以及薄膜剪力为零，即

依据式（1）～式（3），如要满足约束方程（4），可令

假设弹性抛物壳上任意点以一个固有频率进行简谐振动，而其位移可表示为以下形式:

式中，k表示模态阶数;ωk表示第k阶固有频率;Uφk，Uψk和 U3k分别表示子午线方向、圆周方向和横截方向的模态振型函数.

将式（8）～式（10）代入式（5）～式（7）可得

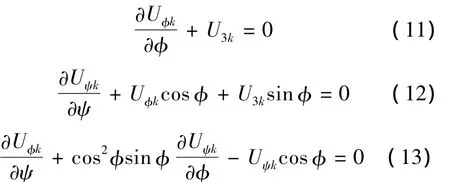
首先将横截方向的模态振型函数写为

式中f3（φ）为变量φ的函数.

将式（14）代入式（11）得:

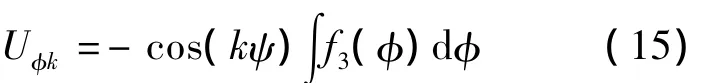
将式（14）和式（15）代入式（12）得:

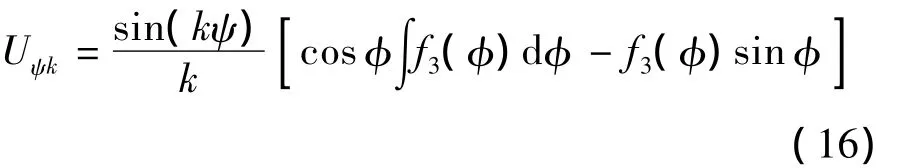
式（18）的通解为

式中c1，c2为任意常数.

由于抛物壳的不同阶次振型的最大幅值并不相同，因此这里引入模态的振动幅值系数Ak，则3个方向上的模态振型函数可以表示为

为了保证当 φ=φ*时，式（5）～式（7）成立，Uφk修改为

由式（19）可以看出，F3（φ）=sin φtan－kφ 和F3（φ）=sinφtankφ均为方程式（18）的特解.

当 F3（φ）=sin φtan－kφ 时，依据式（21）～ 式（23）可求得

针对式（26）的表达式来说，当φ=0时，U3k的值为无穷大，当φ由0→φ*时，tan－kφ越来越小，U3k的值逐渐减少.也就是说，壳的顶点（φ=0）处，其振动幅值为无穷大;而沿着子午线方向由顶点到边缘（0→φ ）移动时，其振动幅值是逐渐减小的.这些均不符合自由边界条件下抛物壳振动的实际情况，因此该组振型函数被排除掉.

当 F3（φ）=sin φtankφ 时，依据式（21）～ 式（23）可求得:

经分析，式（29）所描述的振型函数符合自由边界条件下抛物壳振动的实际情况.依据式（27）～式（29）所表述的振型函数可得到抛物薄壳各阶理论振型的3D图形.

3 抛物薄壳模态分析实验

3.1 抛物薄壳物理模型及模态分析测试平台

本文以DSM Somos-14120树脂为原料，采用激光快速成型法制作了抛物薄壳的物理模型.DSM Somos-14120树脂的机械性能指标为:弹性模量 Y=2.8×109N/m2，质量密度 ρ=1 120 kg/m3（25℃），泊松比 μ=0.35.抛物薄壳的尺寸参数为:开口半径为 a=0.2 m，高度 c=0.1 m，厚度h=1×10－3m.

为满足自由边界条件，采用橡皮筋将抛物薄壳悬吊起来，将壳体的顶点确定为悬吊点，以使悬吊方式对边界条件的影响减到最小.此外，加速度传感器的质量和数量也会对精密柔性壳结构的动态特性产生重要影响，所以实验中只设置一个响应参考点，并选择ICP加速度计（M353B18）对响应参考点进行测量.利用ICP力锤对抛物薄壳进行激励，通过NI动态信号采集卡（NI-PXI44 72）采集数据.图2所示为模态分析测试平台.

图2 自由边界抛物薄壳模态分析测试平台

3.2 模态振型测试及分析

在抛物薄壳模型上沿圆周方向和子午线方向等弧度交叉划分48个节点，应用移动激励点法测试实验模型的动态特性，并通过ModalVIEW模态分析软件进行频响函数分析，最终提取自由边界条件下抛物壳的低阶振型.将抛物壳前三阶实验振型与理论振型、ANSYS分析振型对比，如图3～图5所示.

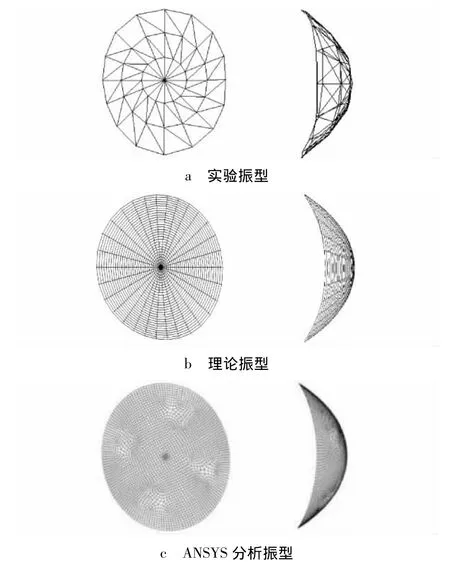
图3 自由边界抛物薄壳第一阶模态形状对比

图4 自由边界抛物薄壳第二阶模态形状对比

图5 自由边界抛物薄壳第三阶模态形状对比

通过模态振型比较可以看出，理论振型、实验振型和ANSYS分析振型在各阶模态均能准确对应，因此可以确认基于membrane简化推导的自由边界抛物薄壳模态振型函数能够正确描述各阶模态振动的实际形状.

4 结论

基于membrane简化，推导出一组完全满足抛物薄壳自由边界条件的模态振型函数，依据所推导的模态振型函数可得到自由边界抛物薄壳上的理论振型.利用模态分析软件ModalVIEW得到自由边界抛物薄壳的低阶模态实验振型.将理论振型、实验振型和ANSYS分析振型进行对比，三者能够较好的吻合，验证了所推导模态振型函数的正确性.

（References）

［1］Tzou Hornsen，Ding Jianghong.Actuator placement and micro-actuation efficiency of adaptive paraboloidal shells［J］.Journal of Dynamic Systems，Measurement and Control，2003，125:577－584

［2］Yue Honghao，Deng Zongquan，Tzou Hornsen.Optimal actuator locations and precision micro-control actions on free paraboloidal membrane shells［J］.Communications in Nonlinear Science and Numerical Simulation，2008，13:2298－2307

［3］罗祖道，潘纪浩.抛物旋转扁壳的轴对称弯曲［J］.力学学报，1963（3）:200－218

Luo Zudao，Pan Jihao.Axisymmetrical bending of shall-ow paraboloidal shell［J］.Acta Mechanica Sinica，1963（3）:200－218（in Chinese）

［4］孙博华.抛物旋转扁壳的一般弯曲问题［J］.力学学报，1989，21（2）:245－249

Sun Bohua.The generalbending problem ofa shallow paraboloidal shell［J］.Acta Mechanica Sinica，1989，21（2）:245－249（in Chinese）

［5］Kayran A，Vinson J R，Ardic E S.A method for the calculation of natural frequencies of orthotropic axisymmetri-cally loaded shells of revolution［J］.Journal of Vibration and Acoustics，1994，116:16－25

［6］张志良，程昌钧.旋转薄壳转点频段的轴对称振动解［J］.固体力学学报，2006，27（2）:630－636

Zhang Zhiliang，Cheng Changjun.Turning-point solution for axisymmetric shell vibrations［J］.Acta Mechanica Solida Sinica，2006，27（2）:630－636（in Chinese）

［7］陈星文，张若京.旋转薄壳自由振动中3类广义相关函数的求解［J］.计算机辅助工程，2008，17（1）:36－38

Chen Xingwen，Zhang Ruojing.Solution to three kinds of generalized related functions in free vibration of revolution shell［J］.Computer Aided Engineering，2008，17（1）:36－38（in Chinese）

［8］张志良，程昌钧.旋转薄壳振动耦合转点问题的一致有效解［J］.中国科学 G 辑，2009，39（8）:1116－1125

Zhang Zhiliang，Cheng Changjun.Uniformly valid solutions of the coupling turning-point problem in revolution shell vibration［J］.Science in China Series G，2009，39（8）:1116－1125（in Chinese）

［9］Al-Khatib O J，Buchanan G R.Free vibration of a paraboloidal shell of revolution including shear deformation and rotary inertia［J］.Thin-Walled Structures，2010，48（3）:223－232

［10］Lin Y K，Lee F A.Vibrations of thin paraboloidal shells of revolution［J］.Journal of Applied Mechanics，1960，27（4）:743－746

［11］Hoppmann W H，Cohen M I，Kunukkasseril V X.Elastic vibrations of paraboloidal shells of revolution［J］.Journal of the A-coustic Society of America，1964，36（2）:349－353

［12］Glockner P G，Tawadros K Z.Experiments on free vibration of shells of revolution［J］.Experimental Mechanics，1973，13（10）:411－421

［13］Kang J H，Leissa A W.Free vibration analysis of complete paraboloidal shells of revolution with variable thickness and solid paraboloids from a three-dimensional theory［J］.Computers and Structures，2005，83:2594－2608

［14］Yue Honghao，Deng Zongquan，Tzou Hornsen.Distributed signal analysis of free-floating paraboloidal membrane shells［J］.Journal of Sound and Vibration，2007，304:625－639

［15］曹富新.简明弹性力学［M］.沈阳:辽宁科学技术出版社，1984:269－270

Cao Fuxin.Concise elasticity［M］.Shenyang:Liaoning Science and Technology Publishing House，1984:269－270（in Chinese）

Mode shape functions of free paraboloidal thin shells

Wang Xinjie Yue Honghao Deng Zongquan

（School of Mechatronic Engineering，Harbin Institute of Technology，Harbin 150001，China）

Based on the membrane theory，a set of mode shape functions for paraboloidal thin shell with free boundary condition were formulated.Low mode shapes of free paraboloidal thin shell were obtained by the way of modal experiment analysis.The theoretical mode shapes based on the mode shape functions were compared with the mode shapes through finite element method and experimental method.The results show that the theoretical mode shapes agree well with the mode shapes through finite element method and experimental method.Then mode shapes of paraboloidal thin shell can be correctly described by the mode shape functions.

paraboloidal thin shell;mode shape function;membrane theory;modal analysis

V 214;TU 33

A

1001-5965（2012）03-0389-05

2010-11-15;< class="emphasis_bold">网络出版时间:

时间:2012-03-09 10:37

www.cnki.net/kcms/detail/11.2625.V.20120309.1037.016.html

国家自然科学基金资助项目（50705017，50675043）;高等学校学科创新引智计划资助项目（B07018）

王新杰（1982－），男，河南郏县人，博士生，wxj_hit@163.com.

（编 辑:文丽芳）