基于速度方向可操作度的机器蛙机构参数优化

胡胜海 杨 奇 何 蕾 谭向全

（哈尔滨工程大学 机电工程学院，哈尔滨 150001）

基于速度方向可操作度的机器蛙机构参数优化

胡胜海 杨 奇 何 蕾 谭向全

（哈尔滨工程大学 机电工程学院，哈尔滨 150001）

以速度方向可操作度作为跳跃性能的评价指标，从机构设计角度寻求改善仿蛙跳跃机器人跳跃性能的方法.在仿蛙跳跃机器人机构模型的基础上，建立了起跳阶段的运动学方程，得到机器人从关节空间到质心运动空间的速度映射关系，结合速度方向可操作度，利用优化算法对仿蛙跳跃机器人的机构参数进行优化，使机器人的跳跃性能达到最佳.优化结果表明，运用速度方向可操作度理论，对跳跃机器人机构参数进行优化研究是有效可行的.

速度方向可操作度;跳跃机器人;跳跃性能;机构参数优化

跳跃机器人能够在诸如考古、星际探测、军事侦察以及反恐活动等特殊领域发挥其优秀的越障能力，适应复杂的地形地貌，提高自身的活动范围，因而备受关注.近年来，随着仿生机器人的发展，模仿生物的肢体结构或按生物跳跃运动机理设计的仿生跳跃机器人日益受到科学家们的青睐，仿人、仿袋鼠、仿蟋蟀、仿蛙等跳跃机器人也因此应运而生［1－4］.仿生机器人实现的基础是合理的机构设计，针对新的机器人模型，机构参数如何设计才能使其运动性能更好，对机器人的设计提出了更高的要求.但对于跳跃机器人的弹跳性能，目前还没有形成系统的评价指标［2］.机器人的可操作性反映了机器人系统对力和运动的全局转换能力，在机械臂的研究中，可操作度指标已被广泛地应用于从机器人手指的运动学设计到冗余自由度机器人的位形优化、关节构型优化等各个方面［5－10］，但对于影响冗余自由度特性的机构参数的研究则相对较少.本文对仿蛙跳跃机器人的机构模型进行合理简化，从机构本身内在的机构特点，建立起跳阶段运动学方程，结合速度的方向可操作性，对机器人的机构参数进行优化，使仿蛙跳跃机器人在任务方向上的跳跃性能达到最佳.

1 仿蛙跳跃机器人机构模型

青蛙跳跃主要依靠两条后腿同时伸展，提供跳跃时向前和向上的力，使起跳前积蓄的能量在跳跃中释放，最终跳离地面.前肢在起跳时辅助支撑地面，调节起跳角度，着地时进行缓冲［4］.青蛙的后肢主要有3个关节，即髋关节、膝关节和踝关节，前肢主要有3个关节，即肩关节、肘关节和腕关节.由于生物的形态经过千百万年的进化，其结构极具合理性，而要用机械来完全仿制生物体几乎是不可能的，因此仅对青蛙的跳跃功能进行提取和简化.

青蛙后肢3个关节各取一个自由度，由于前肢在跳跃中主要用于调节起跳姿态和着地缓冲支撑，简化为2个关节，各取一个自由度，身体的每个部分可简化为杆.简化后的仿蛙跳跃机构模型如图1所示，是一个平面7连杆机构，每个关节处为铰接，并有电机驱动.

图1 仿蛙跳跃机器人机构模型

整个机构在×处被假想地分为2部分:前肢部分和后肢部分，其中后肢部分为4连杆机构，前肢部分为3连杆机构.这2部分通过引入几何约束，来保证躯体始终是一个直的连杆.如图1所示的机构模型中，固定坐标系为xOy，机器人系统的广义坐标向量为

虽然这样会使坐标系冗余，系统描述变得复杂，但是4连杆机构的运动学和动力学方程要比6连杆机构简单，并且2部分机构形式相同只是杆件数目不同，所以可以用相同的方程［6］.

青蛙的一次跳跃运动由3部分组成:起跳阶段、腾空阶段、着地阶段.如图2所示，起跳阶段主要是后肢伸展，利用地面的反作用力实现跳跃;腾空阶段，后肢完全张开，以平衡身体、保证身体在空中的姿态;着地阶段，前肢着地进行缓冲，后肢顺势收回［4］.青蛙在起跳阶段后肢的运动学模型和着地阶段前肢的运动学模型类似，在着地阶段后肢的运动学模型和起跳阶段的前肢运动学模型类似，在腾空阶段的运动为抛物运动.青蛙跳跃的高度和远度取决于起跳瞬时所获得的初始速度的大小，其后腿起跳前积蓄的能量能否充分利用到跳跃中至关重要.

图2 青蛙跳跃过程

由图2可知，青蛙在起跳过程中，主要是后肢起作用，本文重点研究仿蛙跳跃机器人后肢在起跳离地瞬时的运动性能，因此将上述模型中前肢的运动忽略.机构运动学模型简化为如图3所示.

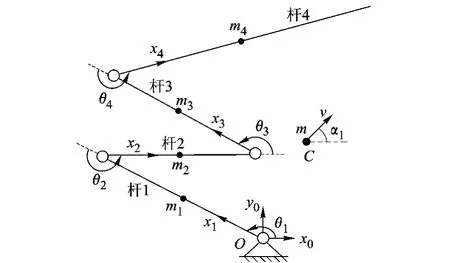
图3 仿蛙跳跃机器人机构运动学模型

起跳阶段青蛙的脚尖与地面的接触点位置不变，以这一点为坐标系原点，建立如图3所示的坐标系，系统的广义坐标向量为

2 速度方向可操作度

机器人速度可操作性是指在当前位形状态下沿指定方向的速度传递特性.在机器人的当前位姿下，系统若能以较小的关节速度使机器人末端沿指定方向获得较大的运动速率，则认为沿此方向机器人位姿的速度可操作性好;若机器人末端沿指定方向不能运动或运动速率低，则认为沿此方向的速度可操作性差［7］.

2.1 速度椭球及可操作度

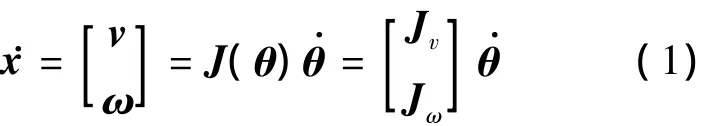
由式（1）可得

对于关节空间Rn中的单位球

映射到操作空间Rm中的椭球

式（4）即为机器人在空间Rm中的广义速度椭球.

定义可操作度为

其物理意义如下.

将J（θ）进行奇异值分解:

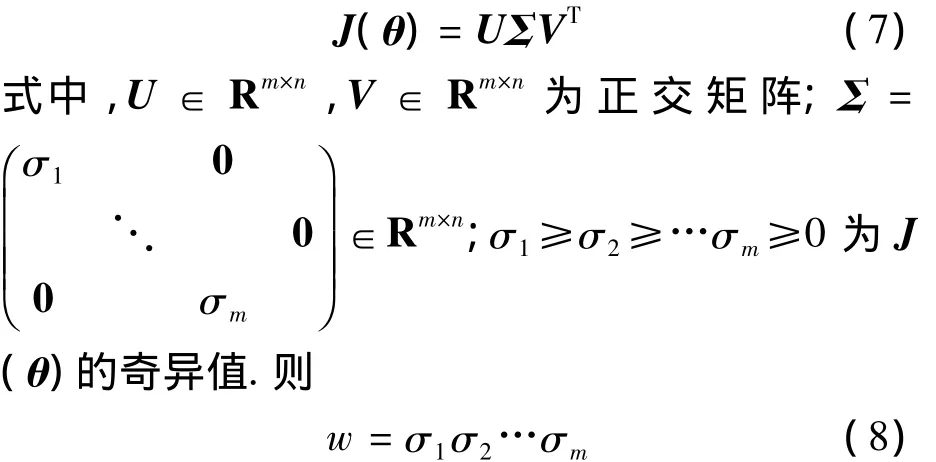
由式（4）可知，机器人末端的速度在Rm中形成了一个椭球，它的主轴方向分别为U的列向量u1，u2，…，um，主轴长度分别为 σ1，σ2，…，σm，体积为{πm/2/Γ［（m/2）+1］}w，Γ（·）为 gamma函数［9］.由此可知，可操作度w与速度椭球的体积成正比，σ1，σ2，…，σm的大小表示在相应主轴方向上的速度传递特性.

w综合评价了机器人的各项灵活性，对机器人的可操作性进行了整体衡量.以w为目标进行运动学优化，即是追求运动的各向同性，实质上是追求速度椭球的体积最大，椭球的中心到椭球面上每一点的长度尽量长.这样w就对非任务方向提出了和任务方向同样的运动要求，不仅浪费了部分优化能力，而且有可能减弱任务方向的运动能力［7］.

2.2 速度方向可操作度的定义

机器人末端在操作空间中的运动速度是一个矢量，可操作度w仅描述了其数值的可操作性，它的方向由任务决定.记机器人末端的运动速度为

式中，β 为速度的大小;p=［cos α1，cosα2，…，cosαm］T∈Rm×1为机器人末端的运动速度方向，α1，α2，…，αm为运动速度与各坐标轴正向之间的夹角.β的物理意义为:速度椭球的中心沿方向p到椭球表面的距离，如图4所示，它反映了机器人在方向p上关节速度和末端速度之间的传递效率，是一种衡量系统可操作度的动态性能指标.

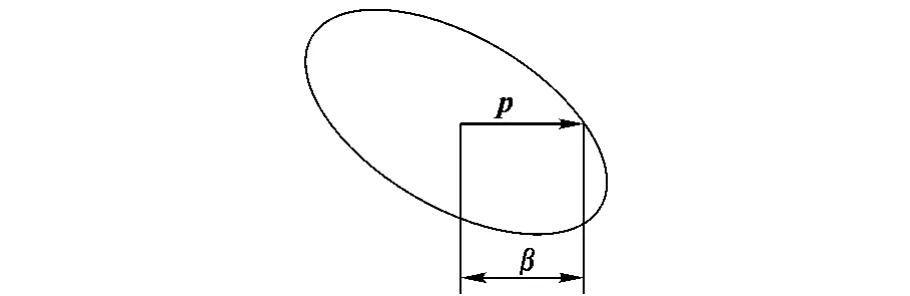
图4 速度方向可操作度示意图

因为x·为速度椭球上的一点，于是将式（9）代入式（4）中有

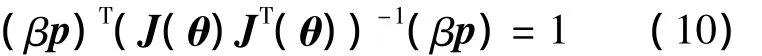
由上式可求得

定义β为机器人在方向p上的速度可操作度.由于速度Jacobian矩阵为机器人关节广义坐标和机构参数的函数，它完全取决于机器人本身的固有性质，故以上定义的速度方向可操作度（VDM，Velocity Directional Manipulability）是从系统固有性质出发衡量机器人在操作空间中的速度传递能力.

同理可定义机器人在方向p1上的线速度可操作度为

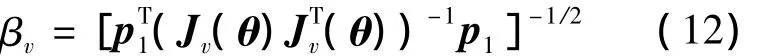
定义机器人在方向p2上的角速度可操作度为

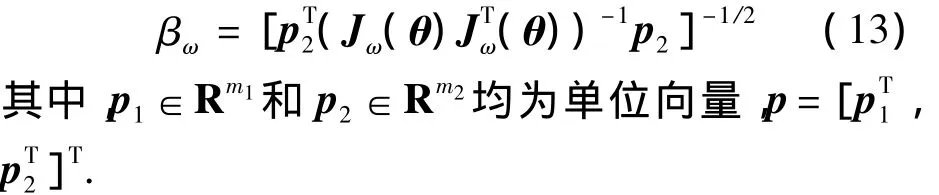
如前所述，令关节速度在空间Rn中为单位球，当这一假设不成立时，需要对关节速度进行如下的规范化 :

再将式（15）代入式（3）得

将式（9）代入上式可得

式（17）即为对关节速度规范化后的速度方向可操作度，同理可得到线速度和角速度的方向可操作度.

3 机器蛙的机构参数优化

对于跳跃机器人，所关心的是它在要求的起跳方向上是否有足够的运动能力，如何评价它在某一位形下沿特定方向的运动能力，并且提高它在这一特定方向的运动能力.

跳跃机器人在跳跃过程中的腾空阶段为自由抛物运动，因此其跳跃的高度和远度取决于起跳时速度的大小和方向.在跳跃任务的方向确定后，当速度的方向可操作性最大时，机器人的速度传递特性最佳，即沿任务方向获得较大的运动速率.一定条件下，仿蛙跳跃机器人跳跃过程中可被视为一个平面冗余自由度机械手，期望其质心获得的速度越大越好，因此可将速度的方向可操作度作为衡量跳跃性能的一个评价指标.

速度方向可操作度一般用来衡量系统由关节空间向末端执行器的操作空间的速度传递能力.对于仿蛙跳跃机器人，本文将建立关节空间到质心运动空间的转换关系，利用速度的方向可操作度衡量其速度传递能力，以此为跳跃性能的评价指标，寻求在给定起跳姿态和方向下，使仿蛙跳跃机器人的跳跃性能达到最佳，即跳的更高更远的机构参数.

仿蛙跳跃机器人运动学模型如图3所示，采用D-H法描述机构运动，将固定坐标系Ox0y0z0设置在机器人脚尖与地面的接触点处，并与地面相固连.机器人各部分杆长分别为 l1，l2，l3，l4，各杆质心分布（质心到其下关节的距离与杆长的比）为 a1，a2，a3，a4，各杆质量为 m1，m2，m3，m4.设机器人质心C点到坐标系原点O的矢径为

每个杆质心的矢径为

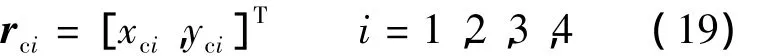
杆4质心矢径的分量xc4和yc4可表示为

式中

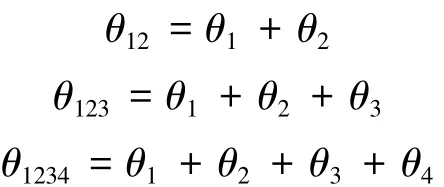
其他杆的质心矢径以此类推进行计算.整个机器人的质心矢径分量可表示为

由式（21）对时间求导，可得质心速度为

式中

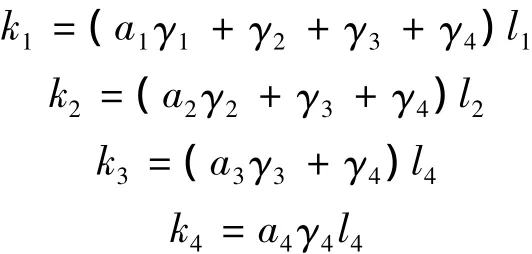
由式（22）可知，此时Jacobian矩阵表示关节空间与质心运动空间速度之间的映射关系.这种运动学模型便于利用“虚拟腿”的概念来规划机器人在起跳阶段的质心轨迹［11］.由式（23）～式（25）可知，Jacobian矩阵可分解为只与状态参量有关的矩阵Q和只与设计参量有关的矩阵B的乘积.将式（9）和式（23）代入式（16），可得

那么，对仿蛙跳跃机器人机构参数优化问题的物理意义可以解释为:通过调整设计参量矩阵B，来改变映射关系式（1），使得式（26）所描述的椭圆在p方向上的速度可操作度β趋于最大.

对于某一跳跃任务，模仿青蛙运动进行轨迹规划后，可得到仿蛙跳跃机器人在起跳离地瞬时的姿态和运动方向，那么基于速度方向可操作度的机构优化描述成数学问题为

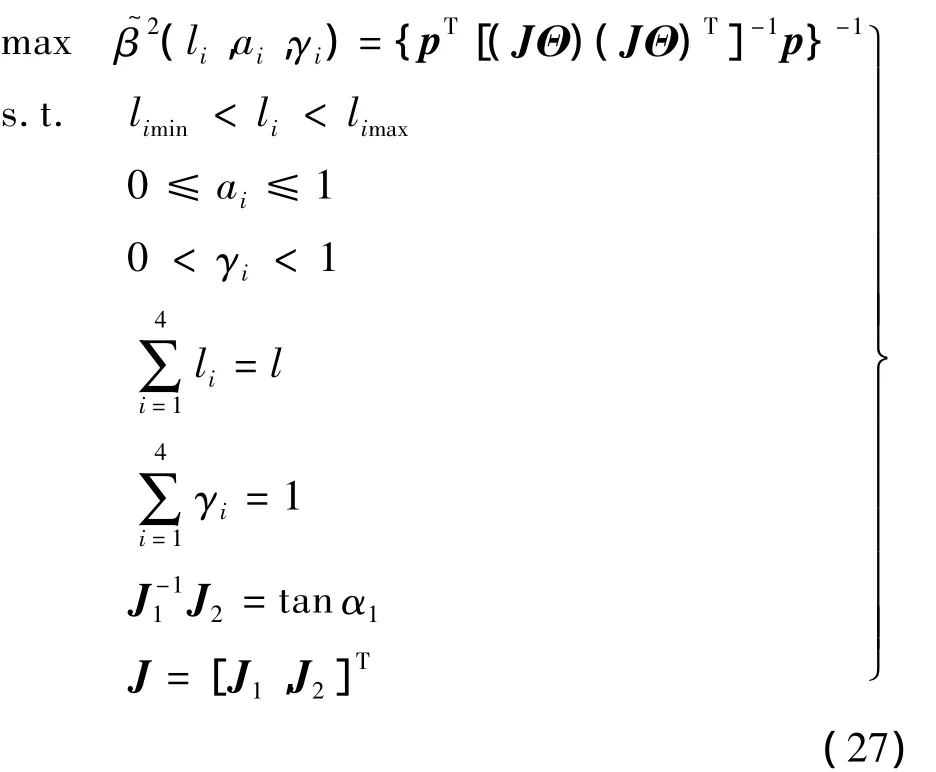
式中，i=1，2，3，4;limin和 limax分别为第 i个杆的最小和最大长度.

4 实例计算

已知仿蛙跳跃机器人起跳离地瞬时姿态为:脚掌与地面夹角为130°，踝关节为117°，膝关节为129°，髋关节为 119°，即 θ=［θ1，θ2，θ3，θ4］T=［130°，243°，170°，231°］T;设定起跳速度方向为p=［cosα1，cos α2］T=［cos59°，cos31°］T;关节速度规范化矩阵 Θ =diag（－8.69，10.0，－5.6，8.74）.已知机构参数及约束为:m=2.85，0.35≤m1≤0.55，0.5≤m2，m3≤0.7，1.1≤m4≤1.3，kg;l=0.712 5，0.065 2≤l1≤0.162 5，0.1≤l2，l3≤0.2，0.25≤l4≤0.45，m.

将上述已知条件代入式（23），采用Matlab中的优化工具箱进行求解，得到机构参数的优化结果如表1所示.图5为在优化设计和初始设计机构参数下的速度椭圆.

对比表1中优化设计和初始设计的机构参数可知，优化后后肢3杆的质心位置均上移，这更有利于跳跃，也符合青蛙的生理结构.优化设计后的速度方向可操作度大于初始设计，也就是说在优化后的机构参数下，仿蛙跳跃机器人获得了更大的起跳速度，即机器人的跳跃性能得到了提高.由表1可知起跳速度提高了6.3%，速度方向可操作度也提高了6.3%，速度方向可操作度与起跳速度成正比，说明用速度方向可操作度衡量跳跃性能是可行的.

表1 机器蛙的机构参数优化结果

图5 优化设计和初始设计的速度椭圆

从图5可看出，沿直线方向，椭圆的中心到椭圆表面的距离增大，即速度传递性能得到提高.充分说明利用速度方向可操作度理论对关节型跳跃机器人进行机构参数的优化研究是有效的.

对于运动任务确定的机器人来说，以速度方向可操作度为指标的优化可以扩展到全域范围，即可对关节工作空间和速度与各坐标轴之间的夹角进行积分，将速度方向可操作度在整个关节空间和各速度方向的均值作为全域速度方向可操作度，可按下式进行计算:

但式（28）的计算量相当大，不利于优化的实施，可对关节空间的轨迹进行离散，找出对速度传递性能有较高要求的某些重要的点，将这些点的速度方向可操作度进行加权平均作为全域度量指标，可得

式中，n 为离散点的个数;ωi为加权系数;为第i点的速度方向可操作度.

5 结论

本文以仿蛙跳跃机器人为研究对象，对其机构模型进行简化，建立了起跳阶段的运动学方程，运用速度方向可操作度对机构参数进行了优化研究.经过实例计算和分析，可得出如下结论:

1）通过建立关节空间到质心运动空间的速度传递关系，采用速度方向可操作度衡量其在任务方向的速度传递性能.当仿蛙跳跃机器人的速度方向可操作度增大时，起跳的初始速度增大，跳跃性能也相应提高.

2）以速度方向可操作度最大为目标，对机器人的机构参数进行优化，使得机构本身的固有性质能够被充分利用，从而提高了机器人的跳跃性能.

以往对于速度方向可操作性的研究，仅限于已知系统位形，确定最佳传速方向或已知运动方向，确定最佳操作位形.本文拓展了速度可操作性理论的应用范围，同时也提出了一种评价跳跃机器人跳跃性能的方法，对跳跃机器人的设计及性能分析有一定参考价值.

（References）

［1］Ryuma Niiyama，Akihiko Nagakubo，Yasuo Kuniyoshi.Mowgli:a bipedal jumping and landing robot with an artificial musculoskeletal system［C］//International Conference on Robotics and Automation.Piscataway，NJ:IEEE，2007:2546－2551

［2］高慧.单足跳跃式仿袋鼠机器人的动力学优化设计［D］.北京:北方工业大学机电工程学院，2008:25－35

Gao Hui.Dynamic optimization and design of one-legged hopping robot with biologically mimic kangaroo［D］.Beijing:College of Mechanical and Electrical Engineering，North China University of Technology，2008:25－35（in Chinese）

［3］张权.仿蟋蟀机器人跳跃运动性能的研究［D］.无锡:江南大学机械工程学院，2009:37－47

Zhang Quan.Research on the locomotion characteristics of the jumping behavior for the bionic cricket robot［D］.Wuxi:School of Mechanical Engineering，Jiangnan University，2009:37－47（in Chinese）

［4］Wang Meng，Zang Xizhe，Fan Jizhuang，et al.Biological jumping mechanism analysis and modeling for frog robot［J］.Journal of Bionic Engineering，2008，5（3）:181－188

［5］徐兆红，吕恬生，王旭阳，等.基于惯性匹配可操作性的跳跃机器人运动优化［J］.上海交通大学学报，2007，42（7）:1154－1158

Xu Zhaohong，Lü Tiansheng，Wang Xuyang，et al.Motion optimization for jumping robot based on inertia matching manipulability［J］.Journal of Shanghai Jiaotong University，2007，42（7）:1154－1158（in Chinese）

［6］Yamakita M，Omagari Y，Taniguchi Y.Jumping cat robot with kicking a wall［J］.Journal of the Robotics Society of Japan，1994，9:934－938

［7］姚建初，丁希仑，战强，等.冗余度机器人基于任务的方向可操作度研究［J］.机器人，2000，22（6）:501－505

Yao Jianchu，Ding Xilun，Zhan Qiang，et al.On task-based directional manipulability measure of redundant robot［J］.Robot，2000，22（6）:501－505（in Chinese）

［8］陈国锋，杨昂岳.双臂机器人位姿的方向可操作性［J］.机器人，1996，18（2）:108－114

Chen Guofeng，Yang Angyue.Direction-oriented manipulability measures of dual-arm robots［J］.Robot，1996，18（2）:108－114（in Chinese）

［9］Tsuneo Yoshikawa.Dynamic manipulability of robot manipulators［J］.Journal of Robotic Systems，1985，2:113－124

［10］Oussama Khatib，Alan Bowling.Optimization of the inertial and acceleration characteristics of manipulators［C］//Proceedings of the 1996 IEEE International Conference on Robotics and Automation.Piscataway，NJ:IEEE，1996，4:2883－2889

［11］魏航信，刘明治.拟人机器人矢状面跑步运动规划［J］.西安电子科技大学学报:自然科学版，2006，33（3）:376－380

Wei Hangxin，Liu Mingzhi.Running motion planning for the humanoid robot in the sagittal plane［J］.Journal of Xidian University，2006，33（3）:376－380（in Chinese）

Mechanism parameters optimization of bionic frog jumping robot based on velocity directional manipulability measure

Hu Shenghai Yang Qi He Lei Tan Xiangquan
（College of Mechanical and Electrical Engineering，Harbin Engineering University，Harbin 150001，China）

The improvement of jumping performance of bionic frog jumping robot was pursued in view of the mechanism design，taking velocity directional measure as an evaluating index of jumping performance.On the basis of bionic frog jumping robot mechanism model，kinematic equations in takeoff phase were established，and the velocity mapping relation of robot from the joint space to the moving space of the center of mass was obtained.Optimal algorithm combined with velocity directional measure was used to optimize the mechanism parameters of the bionic frog jumping robot，in order to optimize the jumping performance of the robot.The optimal result shows that the research on mechanism parameters optimization of jumping robot is feasible by using the theory of velocity directional measure.

velocity directional manipulability measure;jumping robot;jumping performance;mechanism parameters optimization

TH 113.2

A

1001-5965（2012）03-0351-06

2010-11-14;< class="emphasis_bold">网络出版时间:

时间:2012-02-21 11:46

www.cnki.net/kcms/detail/11.2625.V.20120221.1146.002.html

高等学校博士学科点专项科研基金资助项目（20092304120014）

胡胜海（1954－），男，河南伊川人，教授，ski1224@yahoo.com.cn.

（编 辑:文丽芳）