基于小波域的图像椒盐噪声密度估计

李天翼 王明辉 林 涛 余文森

（四川大学 计算机学院，成都 610065）

基于小波域的图像椒盐噪声密度估计

李天翼 王明辉 林 涛 余文森

（四川大学 计算机学院，成都 610065）

提出一种基于小波域的椒盐噪声密度估计方法.利用图像信号在小波域的系数具有稳定近似的分布，以及噪声对小波系数影响的特点，定量地分析了含噪图像的系数幅值直方图与原始图像的系数幅值直方图之间的偏离程度随噪声密度的变化规律，揭示这种变化关系对图像具有强的鲁棒性，从而利用这种关系对噪声进行估计.仿真结果表明，相对于目前方法，提出算法性能更佳，能够获得更准确的估计值和更小的估计偏差.

小波系数;相关系数;直方图;椒盐噪声;密度估计

由于成像过程中的短暂停留而造成的椒盐噪声是影响图像质量的一种典型噪声源.该噪声不仅严重干扰人类的视觉感知，并且经常在边缘提取等处理中引起误操作，因此在图像处理之前通常要进行椒盐噪声的滤除.目前已开发出多种有效的滤噪算法，如标准中值滤波、自适应中值滤波、自适应模糊转换滤波、开关中值滤波、递进开关中值滤波、极值中值滤波、加权中值滤波、大范围相关滤波、基于相关性权值滤波等［1－10］.而在噪声滤除中一个基础性的工作是对噪声的估计，这是因为很多算法都依赖于噪声的参数信息进行处理，并且噪声参数也有助于决策滤波的强度.对于椒盐噪声，唯一的参数就是反映噪声大小的噪声密度.

目前国内外对于噪声估计的报道已很多，但其中多是针对高斯噪声的研究，而对椒盐噪声的估计却鲜见报道.在这方面，国内的张旗和曹占辉等作了有益的探索，并取得不错的结果［11－12］.张旗等在文献［11］中提出的方法是根据小波高频子带系数的方差与椒盐噪声密度有关这一特性，利用多项式拟合求取.而曹占辉等在文献［12］中的方法则是利用图像幅度谱与噪声大小之间的变化规律进行估计.两种方法都在一定程度上解决了噪声密度的估计问题，但还不能达到令人满意的结果.文献［11］方法在噪声密度较低时估计值较好，噪声密度偏高时较差，而文献［12］方法的结果则正好相反.导致估计不准的原因，主要还是来自于两者所采用的依赖关系并不稳健，因而造成较大的偏差.

为此，本文提出一种新的基于小波域的估计算法.该方法首先指出对自然图像而言，其小波高频子带系数具有近似的分布，并将含噪图像的小波系数分布与原始图像的小波系数分布之间的偏离程度进行量化，揭示出这种偏离与噪声密度之间的变化规律，从而利用这种变化关系对噪声进行估计.这种依赖关系相对于文献［11－12］中采用的关系，更能准确反映噪声大小.对大量图像进行计算机仿真，结果表明，本文方法能够获得相当准确的估计值，性能明显优于前面两种算法.

1 噪声对小波系数分布的影响

与图像信号的强度相比，椒盐干扰通常较大，因此在一幅图像中，椒盐噪声通常数字化为图像灰度的极值.在8 bit图像中就是0和255，分别代表胡椒和盐粒噪声，一般情况下认为胡椒和盐粒所占比重相等.这样，假定一幅数字图像椒盐噪声的密度为d，可以为噪声建立如下的数学模型:

式中，f（x，y）和g（x，y）分别表示原始图像和含噪图像中像素点（x，y）的灰度值;P（x）表示取值为x的概率.如果图像像素数为N，意味着图像中有N×d个像素点被污染了.

1.1 自然图像的小波系数分布

小波是近年迅速发展起来的一门新兴技术，广泛应用于图像处理的各个领域.通过一步小波变换，1幅图像被分解成4幅子图像，即近似子带（LL）、水平细节子带（LH）、垂直细节子带（HL）和对角细节子带（HH）.其中LL子带由图像与式（2）的二维尺度函数作内积生成:

而其它3个细节子带由图像与式（3）～式（5）的二维小波函数作内积生成:

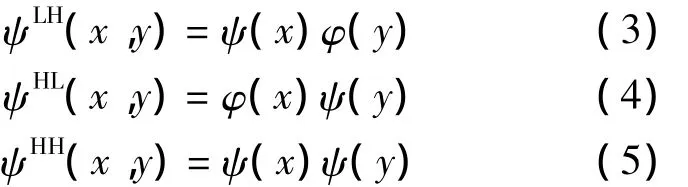
变换过程可以迭代执行若干次，每次都是在上一尺度的近似子带上作分解而实现.图1示出了对一幅图像的二步小波分解.

图1 图像的小波分解示意图

对图像信号而言，其在高频子带中的小波系数具有稀疏性的特点，即大部分系数的幅值接近于或等于零，只有少数系数的幅值较大，这从图1的各个细节子带可以清楚地看出.Mallat在文献［13－14］中提出一种广义高斯模型（GGD，Generalized Gaussian Distribution）来描述这种分布特征:

为直观地描绘小波系数的这种分布，本文以Cameraman（256×256像素）和 Lena（256×256像素）2幅图像为例，对它们的对角子带系数取绝对值，然后作出相应的直方图.原图及对应的直方图如图2和图3所示.由于小波系数正值和负值呈近似对称的分布，所以图中的直方图并未丢失负值部分的信息.

由图2和图3可以看出，2幅图像虽然不同，

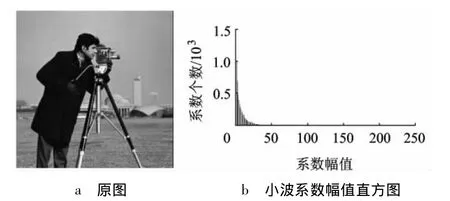
图2 Cameraman图像的小波系数分布

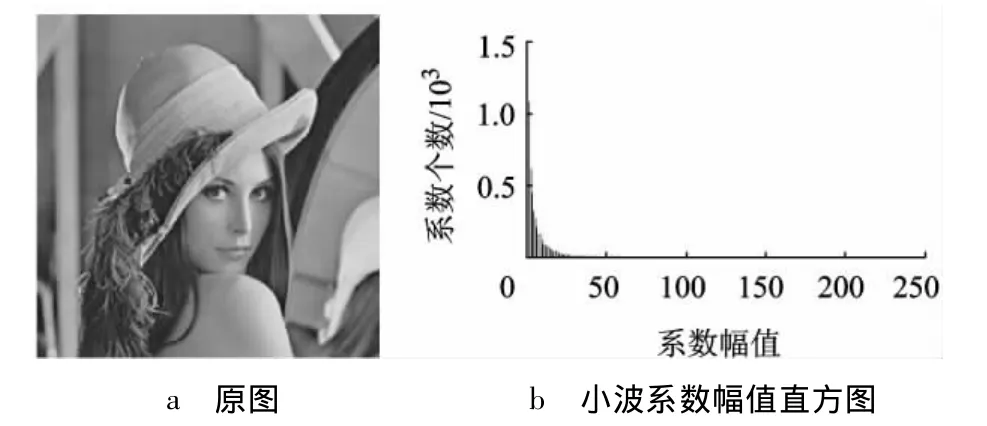
图3 Lena图像的小波系数分布

但由它们生成的对角子带系数幅值的直方图却非常近似.对大量其它图像处理，也生成近似的直方图.当然图像大小不同，纵轴的系数个数会不同，但所占总系数个数的百分比却近似相同.这表明，图像经过小波变换，其高频对角子带中的系数幅值的直方图对图像具有较强的鲁棒性，随具体图像变化较小.于是该直方图可以作为一种通用的特征用于任何图像的计算处理中.为得到鲁棒性更强的结果，本文采用200幅自然图像（包括一些标准测试图），对这些图像的直方图进行统计平均，统计结果称为标准直方图，其数据列在表1中.在计算每一图像的系数幅值直方图时，根据其小波系数可能的幅值范围（例如对8 bit表示，就是0～255），将其均分为6个区间，各区间数据代表的是该区间系数个数占总个数的比例.

表1 标准直方图数据

1.2 噪声对小波系数幅值直方图的影响

对一幅原始图像（不含噪声的自然图像）施加椒盐噪声，该图像就被污染，成为了含噪图像.一幅含噪图像包含若干噪声点，对于椒盐噪声，这些点以灰度极值的形式存在，反映在视觉中就是黑点和白点.引入的噪声点不是图像本身的有机组成成分，与其周围原始图像本身的像素点通常具有较高的灰度梯度.小波变换的特点是对图像平缓的区域生成接近于零的系数，而对灰度急剧变化的部分（如边缘）生成幅值较大的系数.由于噪声点与邻域像素间的灰度差较大，因此相对于原始图像，含噪图像的小波系数中具有较高幅值的系数比例应该较大，而小幅值（或接近于零）的系数比例应较小，反映在系数幅值直方图上，也就是原始图像和含噪图像的对应直方图应有一定程度的偏离.随着噪声密度的增加，噪声点越来越多，那么这种偏离度应该越来越大.为验证这一推断，本文对大量图像施加不同密度的椒盐噪声，作出相应的系数幅值直方图，结果表明了这一推断的正确性.这里以Lena图像为例，其各含噪图像及对应的系数幅值直方图显示在图4中.

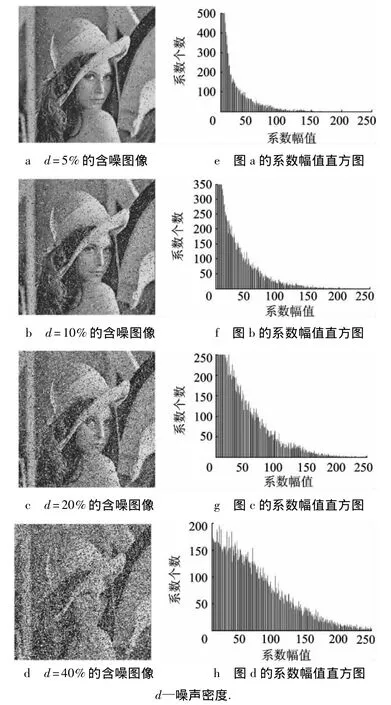
图4 Lena含噪图像及对应的系数幅值直方图

图4直观地显示出了随着噪声密度的增大，含噪图像的系数幅值直方图与原始图像的系数幅值直方图（或者说与标准直方图）的偏离度越来越大.这一关系对其它图像也成立，并且这种偏离对噪声密度非常敏感.例如5%和10%的噪声差别并不太大，但两者的直方图就出现了较大的偏差.这说明含噪图像的系数幅值直方图与标准直方图之间的偏离度适合用于对噪声密度的估计.为此，需要对这种偏离程度进行量化.令标准直方图的数据为hstd（1∶H），其中H是计算直方图时所统计的区间数，反映在hstd中就是所得一维向量的长度.同样令含噪图像直方图的数据为hnoise（1∶H），长度与hstd相等，表示在计算直方图时采用同样的区间划分.hstd（i）表示对处于第i区间的系数统计得出的比例，对hnoise（i）含义类似.这样，可将含噪图像的系数幅值直方图与标准直方图之间的偏离度定义为它们之间的相关系数:

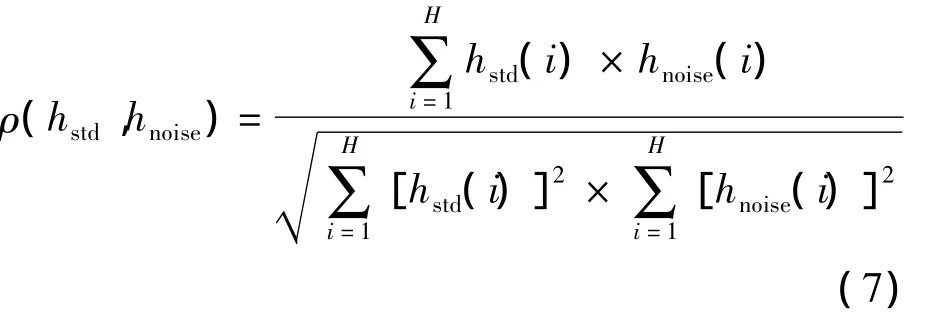
当hstd与hnoise相等，也就是2个直方图完全相同时，所得 ρ（hstd，hnoise）值为 1.随着 hstd与 hnoise差别越来越大，也就是2个直方图越来越偏离时，ρ（hstd，hnoise）值也越来越小，直至为0.所以式（7）的定义能够很好地刻画2个直方图的偏离程度.

对包括图2、图3和图5在内的6幅原始图像分别施加不同密度的椒盐噪声，作小波分解，然后按式（7）计算得到各含噪图像的系数幅值直方图与标准直方图之间的相关系数，部分噪声密度下所得相关系数值列于表2.

图5 参与相关系数计算的实验图像

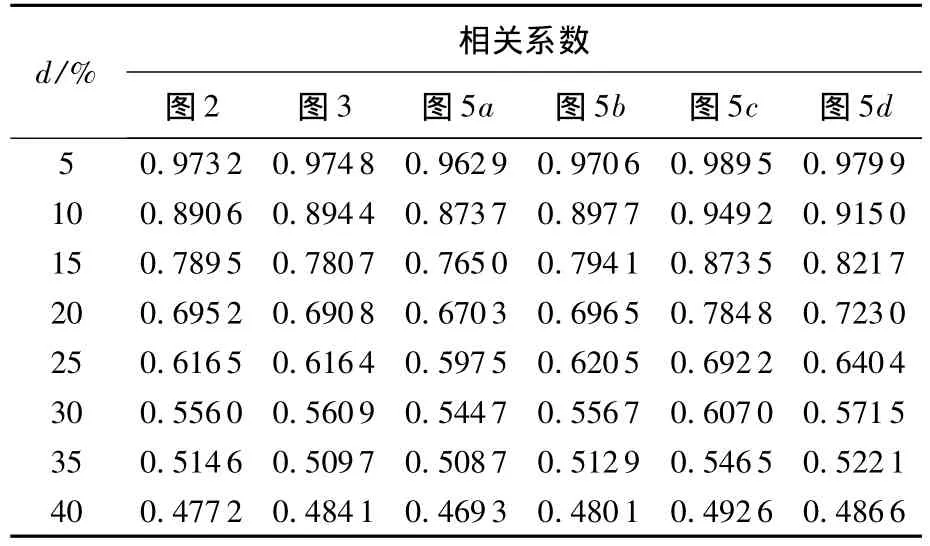
表2 部分噪声密度下相关系数值

对大量其它图像作同样的实验，可以得到近似的结果.对这些数据进行分析可以得出以下2条结论:

1）对任何图像而言，含噪图像的系数幅值直方图与标准直方图之间的相关系数，随噪声密度的增加单调减小.

2）对不同的图像，如果噪声密度相同，则所得相关系数值很接近.通常图像细节较多，所得值偏小，图像较平缓，则所得值偏大，但这种差别并不大.例如图5a（细节非常丰富）和图5c（具有完全平坦的区域），从细节的角度差别巨大，分别代表了2个极端，但在相同噪声密度上所得相关系数值差别却并不太大.对大量其它介于其间的图像，所得值就更加接近.这表明，含噪图像的系数幅值直方图与标准直方图之间的相关系数，极大程度上是由噪声密度决定，受具体图像特征影响较小.

以上分析揭示了含噪图像的系数幅值直方图与标准直方图之间的相关系数非常适合用于对噪声密度的估计.为使这种变化关系更具鲁棒性，将各个噪声密度下对大量图像获得的相关系数值进行平均，部分噪声密度下的统计平均结果示于表3，由表3数据绘出相应的曲线见图6.

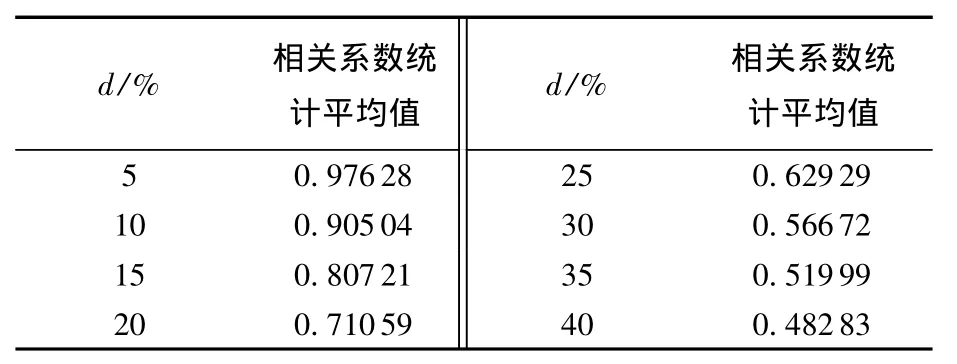
表3 相关系数统计数据

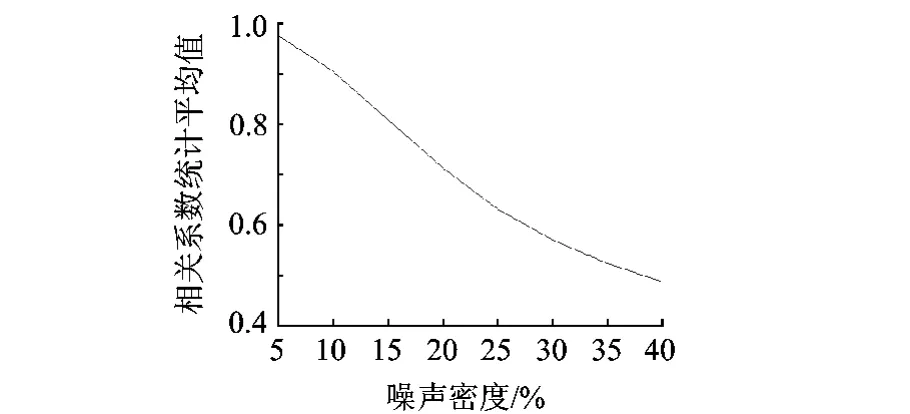
图6 相关系数随噪声密度变化的统计曲线

将统计数据按照最小均方误差准则进行多项式拟合，得出如下拟合公式:

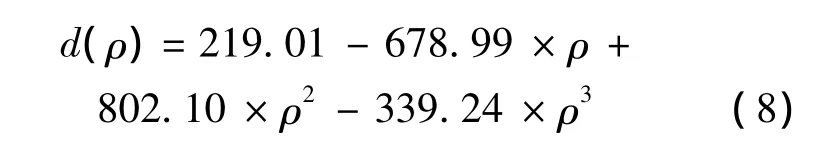
式中，ρ是按式（7）计算所得的相关系数值;d是噪声密度.如果式（8）所得值为γ，则表示噪声密度为γ%.该公式形式化地描述了相关系数与噪声密度之间的变化关系.对于精度要求不高的场合，拟合可以取二次多项式.

2 噪声的估计

上述分析揭示了含噪图像的系数幅值直方图与标准直方图之间的相关系数随噪声密度的变化规律，并将这种关系以式（8）形式化地表达.通过实验论证了这种变化关系对图像具有较强的鲁棒性，这说明利用式（8）通过相关系数值去估计噪声密度能够获得稳健的结果.本文正是利用这样的关系，将表1的标准直方图和式（8）作为先验知识用于含噪图像的估计，获得了比其它方法更优的结果.

对一幅含噪图像的椒盐噪声密度估计描述如下:

1）对含噪图像执行小波分解;

2）对分解所得的高频对角子带系数进行统计，生成系数幅值直方图;

3）对标准直方图与生成的系数幅值直方图，采用式（7）计算它们之间的相关系数;

4）将计算所得相关系数值代入式（8），计算所得即为含噪图像中椒盐噪声密度的估计值.

这里要注意的是对含噪图像作小波分解时，所采用的小波基与获得先验知识所采用的小波基应相同.在本文中采用的小波基为sym4.另外，在生成含噪图像的系数幅值直方图时，所划分的区间数必须与标准直方图所统计的区间数相等，并且这个数目的设定不宜过大，但也不能太小.如果过大，则会对系数随机的微小变化过于敏感，造成估计不稳定.如果太小，则又不能灵敏地检测出2种系数分布之间的差别.本文通过大量实验确定采用的数目为6时是最优的.第1节获得的先验知识就是在这个数目基础上计算得出的.

3 仿真实验

为验证本算法的有效性，本文在Matlab 7.0中［15］进行仿真实验.随机地选取30幅原始图像，分别施加密度为 5%，10%，15%，20%，25%，30%，35%和40%的椒盐噪声，采用本文方法进行估计，估计结果列于表4.为便于比较，文献［11－12］方法的结果也列于表中.为表明本算法的有效性，这里所选择的30幅实验图像与前面获得先验知识所采用的图像是完全不同的2组图像.部分实验图像示于图7.

通过表4的分析可以看出，本文算法相比其它2种方法有明显的改进.除真值为5%时比文献［11］方法略为逊色外，在其它所有密度上的估计都比2种方法更接近真值.文献［11］方法随着噪声密度增大性能越来越差，而文献［12］方法则在噪声较小时误差较大.本文算法并没有这样的特点，在不同的密度上，估计均值总是在真值上下波动，其偏差程度不随噪声大小而变化，这表明本文所依赖的变化关系适用于更宽广的噪声范围.就估计标准差而言，本文算法明显比其它2种方法要小很多.这意味着在本文方法中，对不同图像所得估计值波动较小，这实际上证明了本文算法所采用的变化关系对图像具有强的鲁棒性，几乎不随具体图像的不同而变化，而这个特性对估计结果的可靠性是至关重要的.

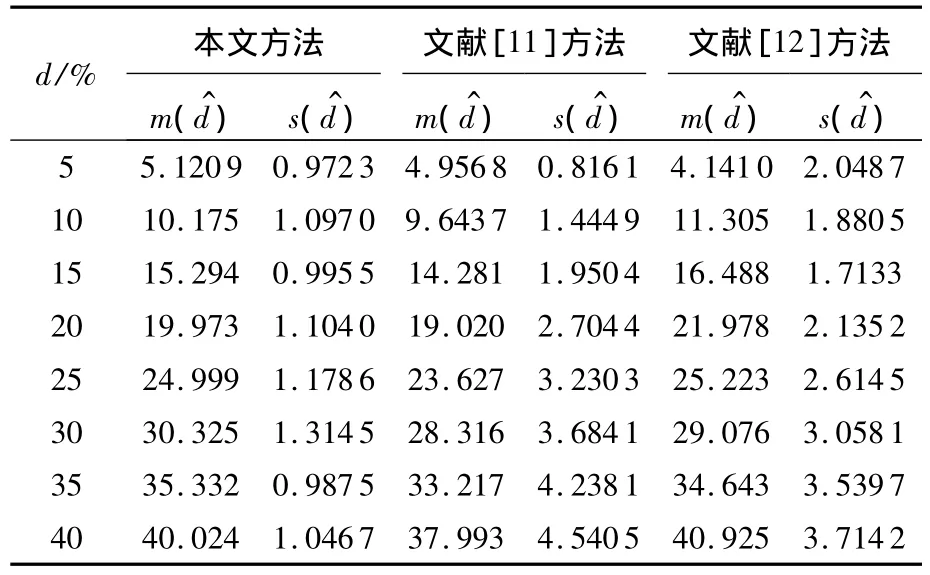
表4 噪声密度估计结果

图7 部分实验图像

4 结论

本文从研究图像信号在小波域的系数分布着手，指出对所有自然图像而言都有近似的系数幅值直方图，进而揭示含噪图像的系数幅值直方图与自然图像的系数幅值直方图之间的偏离程度随噪声密度变化的规律，通过相关系数的引入定量地研究了这种变化关系，并在大量统计数据的基础上通过拟合公式予以形式化的描述.利用这种关系对椒盐噪声密度进行估计，获得了令人满意的结果.

相比现有算法，本文方法所采用的变化关系具有明显的优势:

1）对图像具有更强的鲁棒性.这决定了本文算法的估计值更准确.

2）适用于更宽广的噪声范围.这决定了本文算法的应用面更广.

不过，在噪声密度特别大（＞70%）的情况下，本文方法性能有所降低.这可以解释为噪声密度很大时，噪声点与噪声点聚集在一起，这时噪声点的邻域中也包含很多噪声点，并且这些噪声点有一半的概率与中心噪声点像素值相等，这样中心噪声点与周围像素的灰度差别不仅不大，反而非常接近，所得小波系数的幅值自然不会偏大.这时含噪图像的系数幅值直方图与标准直方图之间的偏离度不再随噪声密度单调变化，由此来估计噪声自然不会得到准确的结果.针对高椒盐噪声估计不准的问题也同样存在于包括文献［11－12］的其它算法中.如何提高算法在高椒盐噪声下的估计性能，是下一步的研究方向.

（References）

［1］Gallagher Jr N C，Wise G L.A theoretical analysis of properties of the median filters［J］.IEEE Trans on Acoustics Speech，Signal Processing，1981，29（1）:1136－1141

［2］Hwang H，Haddad R A.Adaptive median filters:new algorithms and results［J］.IEEE Transactions on Image Processing，1995，4（4）:499－502

［3］Xu H X，Zhu G X，Peng H Y.Adaptive fuzzy switching filter for images corrupted by impulse noise［J］.Pattern Recognition Letters，2004，25（15）:1657－1663

［4］Qin Peng，Ding Runtao.Ordering threshold switching median filter［J］.Journal of Image and Graphics，2004，9（4）:412－416

［5］Wang Z，Zhang D.Progressive switching median filter for the removal of impulse noise from highly corrupted images［J］.IEEE Transactions on Circuits System，1999，46（1）:78－80

［6］Xing Z J，Wang S J，Deng Haojiang，et al.A new filtering algorithm based on extremum and median value［J］.Journal of Image and Graphics，2001，6（6）:533－536

［7］Yang R K，Yin L，Gabbouj M，et al.Optimal weighted median filtering under structural constraints［J］.IEEE Transactions on Signal Processing，1995，43（3）:591－604

［8］Wang Z，Zhang D.Restoration of impulse noise corrupted images using long-range correlation［J］.IEEE Signal Processing Letters，1998，5（1）:4－7

［9］Song Y，Li M T，Sun L N.Image salt＆ pepper noise selfadaptive suppression algorithm based on similarity function［J］.Acta Automatic Sinica，2007，33（5）:474－479

［10］Wang B，Pan Q.Soft-threshold histogram weighted filtering with correlativity for high density salt-pepper noise images［J］.Acta Electronica Sinica，2007，35（7）:1347－1351

［11］Zhang Q，Liang D Q，Fan X.Identifying of nosie types and estimating of noise level for a noisy image in the wavelet domain［J］.Journal of Infrared Millimeter Waves，2004，23（4）:281－285

［12］Chao Z H，Li Y J，Zhang K.Estimation of salt＆ pepper noise on the magnitude spectrum［J］.Infrared Technology，2006，28（9）:549－551

［13］Mallat S G.A theory for multiresolution signal decomposition:the wavelet representation［J］.IEEE Trans Pattern Analysis and Machine Intell，1989，11（7）:674－693

［14］Mallat S G.A wavelet tour of signal processing［M］.2nd ed.Beijing:China Machine Press，2006

［15］Gonzalez R C，Woods R E，Eddins S L.Digital image processing using matlab［M］.Upper Saddle River，New Jersey:Prentice Hall，2005

Estimation of salt-pepper noise in images in wavelet domain

Li TianyiWang Minghui Lin Tao Yu Wensen
（College of Computer Science，Sichuan University，Chengdu 610065，China）

A novel approach was proposed for estimating the density of salt-pepper noise in images using wavelet transform.On the basis of the fact that the wavelet coefficients of all natural images conform to stable and close distribution，as well as such distribution of the noisy image may be influenced by the noise，the proposed algorithm exhibits how the wavelet coefficients magnitude histogram of the noisy image deviates from that of original image along with the density of the salt-pepper noise in quantitative form，and indicates that the degree of such deviation is nearly determined by the noise density，i.e.，the change relation is robust to image traits.The proposed algorithm thus takes advantage of this relation to make estimation.Compared with those of existing methods，simulation results show that the proposed approach has more exact estimation value and less deviation.

wavelet coefficient;correlation coefficient;histogram;salt-pepper noise;density estimation

TP 391

A

1001-5965（2012）02-0239-05

2010-11-08;< class="emphasis_bold">网络出版时间:

时间:2012-02-21 11:47;

CNKI:11-2625/V.20120221.1147.026

www.cnki.net/kcms/detail/11.2625.V.20120221.1147.026.html

李天翼（1970－），男，四川合江人，博士生，scu_lty@eyou.com.

（编 辑:文丽芳）