基于伪寿命的加速退化机理一致性边界检验

林逢春 王前程 陈云霞 康 锐

（北京航空航天大学 可靠性与系统工程学院，北京 100191）

基于伪寿命的加速退化机理一致性边界检验

林逢春 王前程 陈云霞 康 锐

（北京航空航天大学 可靠性与系统工程学院，北京 100191）

根据寿命型随机变量的加速机理一致性条件，提出一种基于伪寿命的加速退化机理一致性边界检验方法，通过由低到高逐一对各个加速应力水平下的退化机理一致性进行检验，来确定加速退化机理一致性的边界应力水平.针对工程常用的两类寿命型分布——对数正态分布和Weibull分布，分别以对数标准差和形状参数为退化机理表征量，在产品伪寿命估计的基础上建立了退化机理表征量齐性检验的F统计量，导出了退化机理一致性检验拒绝域的解析式，给出了退化机理一致性边界检验的具体步骤.该方法能够充分利用多个应力水平下表征产品退化机理一致的横向信息，有效提高了检验的精度.以某镀膜平板玻璃热退化机理一致性边界温度的确定为例，分析说明了该方法的合理性与有效性.

机理一致性;加速退化试验;伪寿命;F检验

加速退化试验通过提高应力水平快速激发产品缺陷、加速产品退化过程，以在较短时间内得到产品的退化信息，并结合加速方程实现对产品寿命和可靠性的有效评定.基于加速退化试验的可靠性评估方法弥补了传统可靠性评估技术对无失效数据或极少失效数据统计分析时精度不高的缺点，是解决长寿命、高可靠产品寿命与可靠性问题的重要技术途径.国内外学者对此开展了大量研究，并已在武器装备、航空航天和机电产品等各领域得到了广泛的应用［1－5］.

基于加速退化试验的可靠性评估理论是建立在加速应力水平和正常应力水平下产品退化机理一致的基础上.如果产品退化机理发生改变，则试验所得到的信息不能反映正常应力水平下产品退化失效的真实规律，也就无法正确评估正常应力水平下产品的寿命和可靠性水平，从而严重降低加速退化试验分析结果的合理性和有效性［6］.为此，工程实际中通常在开展加速退化试验之前先进行强化试验等预试验，以判断产品是否具有退化特征、产品退化是否具有可加速性，并确定加速退化试验的应力水平极限［7］.然而，强化试验等预试验往往以主观定性分析为主，对于产品的退化性和退化可加速性尚可进行合理的判断，但是同一退化现象往往可由多种截然不同的机理导致，单纯依赖退化信息的定性分析很难准确分辩主导退化机理的异同，也就无法准确确定满足退化机理一致性的应力范围，给加速退化试验设计和分析带来很大的风险和困难［8］.为了减小试验风险，应力水平极限的确定通常偏于保守，这不仅削弱了加速退化试验在节约试验时间方面的作用，也会由于试验应力水平区间较短变相增加外推长度导致加速退化试验数据分析精度和难度的增加.因此，如何充分挖掘预试验中的有效信息，准确合理地确定应力水平极限，是加速退化试验实施的关键和难点所在.为此，本文通过对预试验各个加速应力水平下的产品伪寿命估计进行定量分析，建立加速退化机理一致性的边界检验方法，并依此确定退化机理一致性边界应力水平，可以为加速退化试验的设计和分析提供定量依据.

1 基本思想

对于加速退化试验，可以根据退化数据获得不同加速应力水平下各个产品的伪寿命估计，形成各个加速应力水平下产品的伪寿命样本.因此，依据寿命型随机变量加速机理一致性条件，可以对退化机理一致性进行检验，从而确定加速退化机理一致性的边界应力水平.

设共有 k个加速应力水平 S1＜S2＜…＜Sk.首先检验最低的两个加速应力水平S1和S2是否满足退化机理一致性条件.如果经检验认为S1和S2下的退化机理一致，则追加S3，并检验S3下的退化机理是否与S1和S2下的一致.如此由低到高逐一添加加速应力水平进行退化机理一致性检验，直至经检验认为当前最高应力水平Sq下的退化机理与其它较低应力水平 S1，S2，…，Sq－1下的退化机理存在显著差异.将低于Sq－1的应力水平下的退化机理记为A，高于Sq的应力水平下的退化机理记为B，则退化机理在应力水平区间［Sq－1，Sq］由 A改变为 B，此时将 Sq－1和 Sq分别作为退化机理A的一致性上边界应力水平下限SA，max，L和上限SA，max，U，它们同时也分别是退化机理 B 的一致性下边界应力水平下限 SB，min，L和上限 SB，min，U.至此，退化机理A一致性上边界检验结束.若经检验当前试验最高加速应力水平Sk下的退化机理与较低应力水平 S1，S2，…，Sk－1下的退化机理之间不存在显著差异，则只能确定退化机理A一致性上边界高于Sk，而将Sk作为退化机理A一致性上边界应力下限 SA，max，L.退化机理 A一致性边界检验流程见图 1.当 SA，max，U=Sq＜Sk时，可以继续对Sq＜Sq+1＜…＜Sk进行分析，确定退化机理 B的一致性上边界应力水平.下面针对工程常见的寿命分布——对数正态分布和Weibull分布建立退化机理一致性边界检验方法.

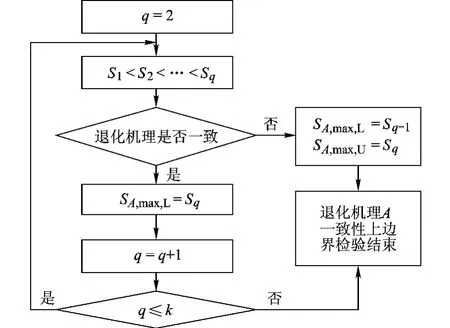
图1 退化机理A一致性边界检验流程

2 对数正态分布下一致性边界检验

当产品退化失效的伪寿命服从对数正态分布时，设tij为第i个加速应力水平Si下第j个产品的伪寿命，i=1，2，…，k;j=1，2，…，ni.并设 tij服从对数正态分布，有

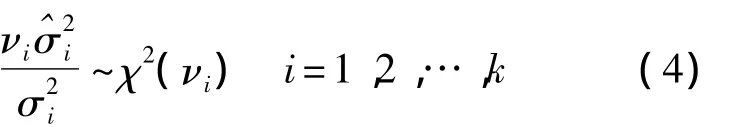
其中 νi=ni－1.

假设应力水平 S1＜S2＜…＜Sq－1（q=2，3，…，k）满足退化机理一致性条件，即有［8－11］

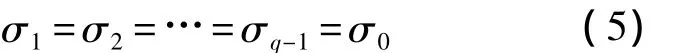
其中σ0为常数.显然，根据χ2分布的可加性有

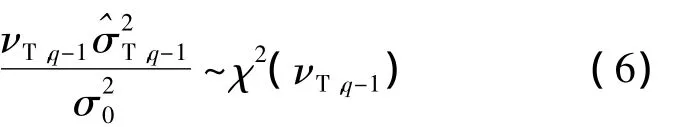
式中

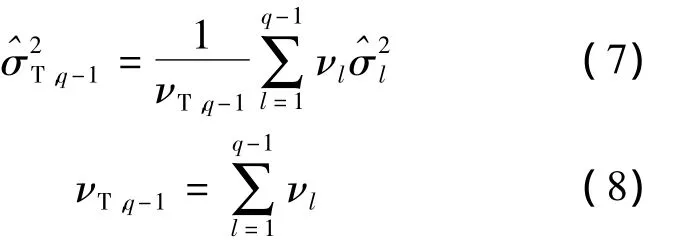
如果应力水平 Sq的退化机理与 S1，S2，…，Sq－1下的退化机理一致，则应有

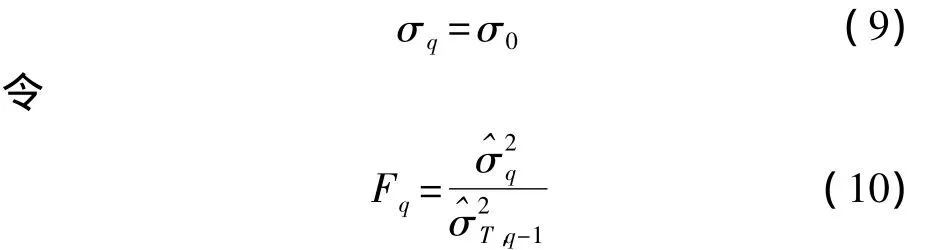
可以证明，当式（9）成立时，有

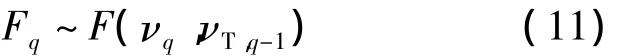
因此，在给定的显著性水平α下，式（9）的拒绝域可由下式给出

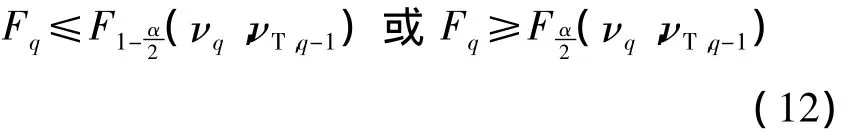
其中 Fα（νq，νT，q－1）为分布 F（νq，νT，q－1）的上 α 分位数.如果式（12）成立，则可认为 σq≠σ0，即 Sq下的退化机理与 S1，S2，…，Sq－1下的存在显著差异.

通过强化试验等预试验确定退化机理一致性边界时，一般试验时间较短，很难直接得到产品的伪寿命，此时可以先采用退化轨迹法等得到伪寿命估计，然后用伪寿命的估计值代替其真值进行退化机理一致性检验.对数正态分布情况下加速退化机理一致性边界检验的具体步骤如下:

1）根据产品退化数据估计各个产品的伪寿命，第i个加速应力水平Si下第j个产品的伪寿命估计仍记为 tij，i=1，2，…，k;j=1，2，…，ni.

3）令q=2.

4）对于加速应力水平 S1，S2，…，Sq，由式（10）计算检验统计量Fq.

5）对于给定的显著性水平α，判断Fq是否落入式（12）给出的检验拒绝域.

6）如果式（12）成立，则退化机理一致性上边界应力下限 Smax，L=Sq－1，上限 Smax，U=Sq，检验结束.

7）如果式（12）不成立，则退化机理一致性上边界应力下限 Smax，L=Sq.令 q=q+1，若 q≤k，则回到步骤4）继续进行检验，否则检验结束.

3 Weibull分布下一致性边界检验

当伪寿命服从Weibull分布时，设tij为第i个加速应力水平Si下第j个试样的伪寿命，并设tij服从Weibull分布，有

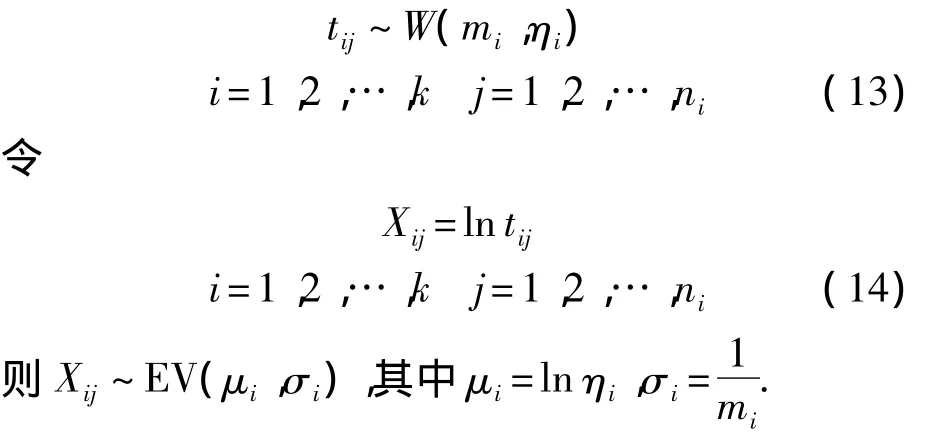
对第i个加速应力水平Si下的Xij进行分析，得到σi的最佳线性无偏估计（BLUE，Best Linear Unbiased Estimation）^σi.当ni较大时，有［12］

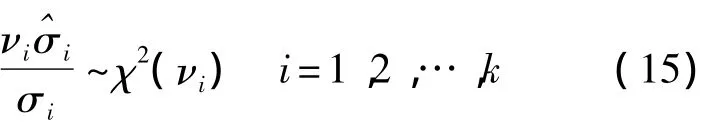
假设应力水平 S1＜S2＜…＜Sq－1（q=2，3，…，k）满足退化机理一致性条件，即有［8－11］

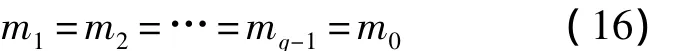
则有

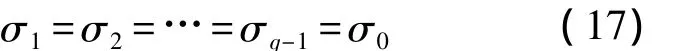
其中m0和σ0为常数.此时，根据χ2分布的可加性有

如果应力水平 Sq的退化机理与 S1，S2，…，Sq－1下的退化机理一致，则应有当应力水平 Sq与 S1，S2，…，Sq－1下的退化机理一致，即式（21）成立时，式（11）仍然成立.因此，在给定的显著性水平α下，σq=σ0的检验拒绝域仍可由式（12）给出.如果式（12）成立，则可认为σq≠σ0，即 Sq下的退化机理与 S1，S2，…，Sq－1下的存在显著差异.实际计算过程中，νq和 νT，q－1通常不为整数，此时可由 Paulson-Takeuchi公式［14］近似计算F分位数，即

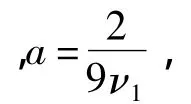
同样，采用产品的伪寿命估计值建立Weibull分布情况下加速退化机理一致性边界检验方法，具体步骤如下:

1）根据产品退化数据估计各个产品的伪寿命，第i个加速应力水平Si下第j个产品的伪寿命估计仍记为 tij，i=1，2，…，k;j=1，2，…，ni.

2）根据式（14）将tij变化为Xij，并采用BLUE方法对其进行分析得到σi的点估计^σi.

3）令q=2.

4）对于加速应力水平 S1，S2，…，Sq，由式（22）计算检验统计量Fq.

5）对于给定的显著性水平α，判断Fq是否落入式（12）给出的检验拒绝域.

6）如果式（12）成立，则退化机理一致性上边界应力下限 Smax，L=Sq－1，上限 Smax，U=Sq，检验结束.

7）如果式（12）不成立，则退化机理一致性上边界的应力区间下限 Smax，L=Sq.令 q=q+1，若q≤k，则回到步骤4）继续进行检验，否则检验结束.

4 应用实例

在与某单位合作开展的镀膜平板玻璃贮存期评定研究中，加速试验进行前进行了3个样品的高温步进强化试验，试验温度范围为40～300℃，试验剖面见图2，其中t为累积保温时间.

试验过程中对镀膜总阻值进行在线监测，监测数据表明总阻值与时间具有线性相关关系.图3给出了其中1个样品不同温度下的总阻值监测结果，其中t为各个温度下的保温时间.采用线性模型建立不同温度下镀膜总阻值随保温时间的退化轨迹为

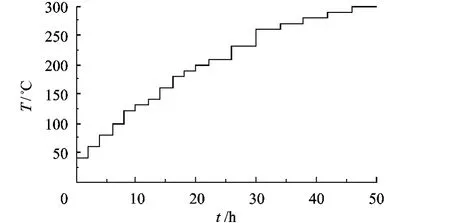
图2 高温步进强化试验剖面

其中，Rij和Rij0为温度Ti下第j个样品的总阻值及其初始值;bij为Ti下该样品的总阻值变化速率.该产品要求贮存期内镀膜总阻值变化率不超过10%，据此得到温度Ti下第j个样本的伪寿命估计为其中R0j0为高温步进强化试验前第j个样本的总阻值.图4给出了各个样品不同温度下的伪寿命估计.

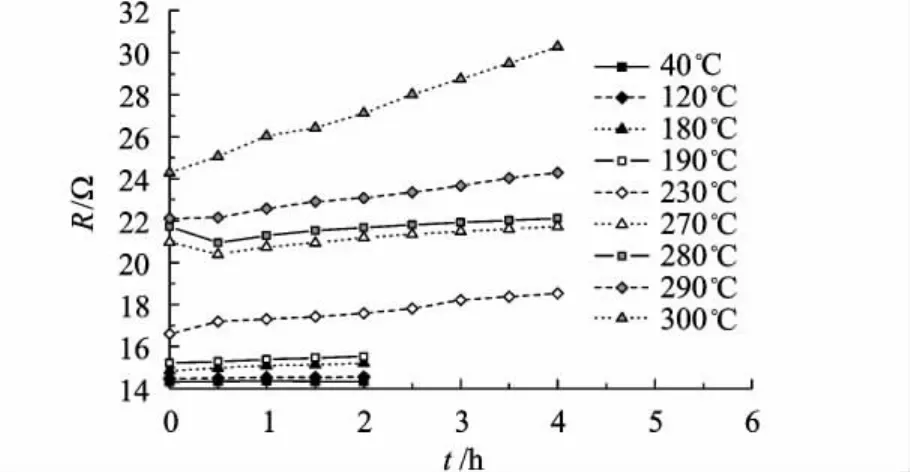
图3 某样品总阻值监测结果

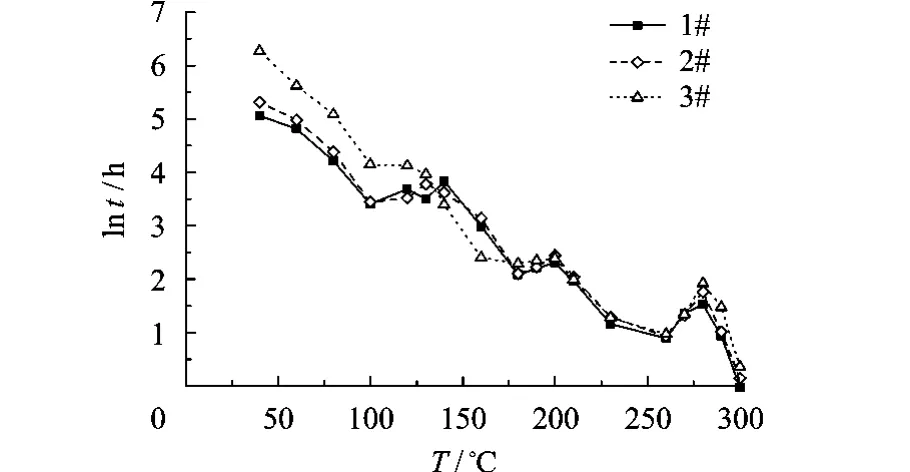
图4 不同温度下的伪寿命估计

根据工程经验，该产品寿命分布服从对数正态分布，采用本文第2节方法对图4数据进行处理.首先，由40℃开始进行退化机理一致性边界检验，结果表明190℃下的退化机理与较低温度的退化机理存在显著差异，即退化机理在180～190℃内发生改变.将40～180℃和190℃下的退化机理分别记为A和B，则180℃和190℃分别为退化机理A的一致性上边界温度下限和上限，同时也是退化机理B的一致性下边界温度下限和上限.然后，由190℃开始进行退化机理B的一致性边界检验，经检验280℃下的退化机理与190～270℃下的退化机理存在显著差异.将280℃下的退化机理记为C，则270℃和280℃分别为退化机理B的一致性上边界温度下限和上限，同时也是退化机理C的一致性下边界温度下限和上限.最后，由280℃开始进行退化机理C的一致性边界检验，经检验退化机理在280～300℃未发生明显改变，将300℃定为退化机理C的一致性上边界温度下限.不同阶段计算得到的检验统计量列于表1.通过上述分析认为该产品在40～300℃间存在3种不同的退化机理，180～190℃，270～280℃分别为退化机理A改变为B、B改变为C的过渡温度区间.

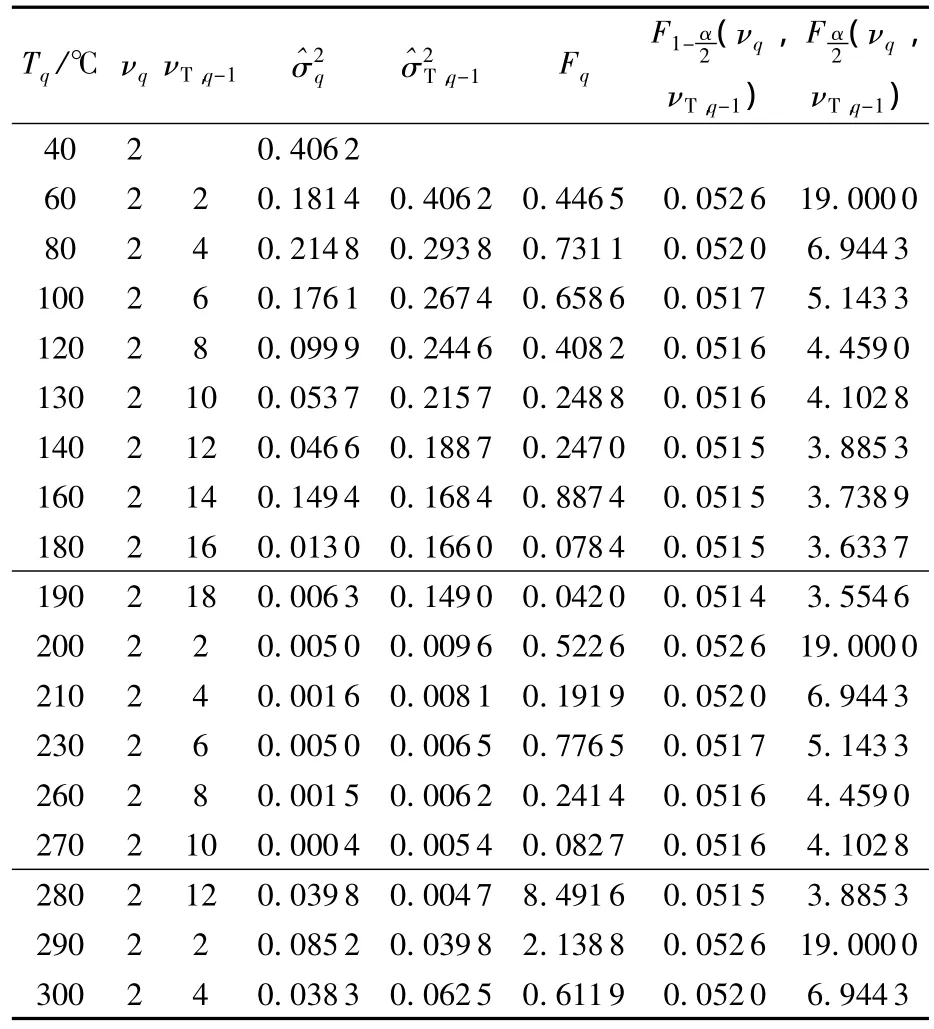
表1 退化机理一致性边界检验统计量

试验过程中同时对表面形貌和透过率变化情况进行了监测，分析结果表明该产品在40～300℃存在3种热退化机理:①低于180℃时，产品热退化由氧化和结构弛豫引起，对应于退化机理A;②180～270℃，主导退机理改为氧化和结晶，对应于退化机理B;③高于270℃时，主导退机理再次发生改变，改为氧吸附和结晶，对应于退化机理C.

根据图3可以看出，总阻值变化速率在270～280℃内相比较低温度有所降低，并在高于280℃后随温度升高迅速增大，同时表面形貌和透过率测试结果表明在高于280℃后它们随温度升高存在显著退化，这与退化机理B到C的改变有关，通过定性分析可以大致确定退化机理B到C的改变温度.但是，在180～190℃附近，总阻值变化速率、表面形貌和透过率均无明显变化，通过定性分析很难发现退化机理A到B的改变.而根据表1可知，190～270℃内产品伪寿命的对数标准差明显较低，采用本文方法能够准确判断出40～180℃和190℃下伪寿命的对数标准差存在显著差异，进而得出产品在温度区间（180，190）℃内发生退化机理改变的结论.由此可见，本文方法能够对退化机理一致性边界进行有效检验，避免了定性分析难以分辩退化机理A和B引起的试验设计和分析的风险.

为了保证加速退化试验的合理性和有效性，该产品加速退化试验的试验温度不应高于正常应力水平下退化机理的一致性上边界，即最高试验温度应低于180℃.

5 结束语

本文给出了一种基于伪寿命的加速退化机理一致性边界检验方法，通过对不同加速应力水平下的产品伪寿命估计进行分析，确定退化机理一致性边界应力水平.该方法采用F统计量对待检验与已检验应力水平下的退化机理一致性进行检验，与传统的多应力水平Bartlett检验相比，避免了Bartlett统计量的分布近似问题，并且能够充分利用已检验应力水平下退化机理一致的横向信息，可以有效提高检验精度.

文中分别针对产品伪寿命服从对数正态分布和Weibull分布的情况展开了详细的讨论，并可进一步推广到其它寿命分布的情况.产品的伪寿命分布可以根据工程经验、历史数据或同类/相似产品的已有寿命信息确定，并通过伪寿命估计的拟合优度检验加以验证.当根据工程经验、历史数据或同类/相似产品信息无法确定产品的伪寿命分布时，可选择拟合度较高的分布作为产品伪寿命分布.

采用本文方法对某镀膜平板玻璃高温步进强化试验数据进行了分析，确定了退化机理的一致性边界应力水平，与产品实际退化机理分析结果相符，表明了该方法的合理、有效性.

（References）

［1］Wu S J，Shao J.Reliability analysis using the least squares method in nonlinear mixed-effect degradation models［J］.Statistica Sinica，1999，9（3）:855－877

［2］Liao H T，Elsayed E A.Reliability prediction and testing plan based on an accelerated degradation rate model［J］.International Journal of Materials and Product Technology，2004，21（5）:402－422

［3］Liao H，Elsayed E A.Reliability inference for field conditions from accelerated degradation testing［J］.Naval Research Logistics，2006，53（6）:576－587

［4］Park J I，Bae S J.Direct prediction methods on lifetime distribution of organic light-emitting diodes from accelerated degradation tests［J］.IEEE Transactions on Reliablity，2010，59（1）:74－90

［5］赵建印，刘芳.加速退化失效产品可靠性评估方法［J］.哈尔滨工业大学学报，2008，40（10）:1669－1671

Zhao Jianyin，Liu Fang.Reliability assessment from accelerated performance degradation tests［J］.Journal of Harbin Institute of Technology，2008，40（10）:1669－1671（in Chinese）

［6］Hu J M，Baker D B，Dasgupta A，et al.Role of failure-mechanism identification in accelerated testing［J］.Journal of the IES，1993，26（4）:39－45

［7］McLean H W.HALT，HASS，and HASA explained:accelerated reliability techniques［M］.Revised Edition.Milwaukee:American Society for Quality，Quality Press，2009

［8］茆诗松，王玲玲.加速寿命试验［M］.北京:科学出版社，2000:85，139

Mao Shisong，Wang Lingling.Accelerated life testing［M］.Beijing:Science Press，2000:85，139（in Chinese）

［9］赵宇，杨军，马小兵.可靠性数据分析教程［M］.北京:北京航空航天大学出版社，2009:184－188

Zhao Yu，Yang Jun，Ma Xiaobing.Reliability data analysis tutorial［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，2009:184－188（in Chinese）

［10］周源泉，翁朝曦，叶喜涛.论加速系数与失效机理不变的条件（I）——寿命型随机变量的情况［J］.系统工程与电子技术，1996，18（1）:55－67

Zhou Yuanquan，Weng Zhaoxi，Ye Xitao.Study on accelerated factor and condition for constant failure mechanism（I）—the case for lifetime is a random variable［J］.Journal of Systems Engineering and Electronics，1996，18（1）:55－67（in Chinese）

［11］孙祝岭.失效机理不变的假设检验［J］.电子产品可靠性与环境试验，2009，27（2）:1－5

Sun Zhuling.Hypothesis testing for constant failure mechanism［J］.Electronic Product Reliability and Environmental Testing，2009，27（2）:1－5（in Chinese）

［12］戴树森，费鹤良，王玲玲，等.可靠性试验及其统计分析:上册［M］.北京:国防工业出版社，1983:536－539

Dai Shusen，Fei Heliang，Wang Lingling，et al.Reliability testing and its statistical analysis:vol.1［M］.Beijing:National Defense Industry Press，1983:536－539（in Chinese）

［13］中国电子技术标准化研究所.可靠性试验用表［M］.北京:国防工业出版社，1987

The Chinese Research Institute for Electron Technology.Handbook of table for reliability testing［M］.Beijing:National Defense Industry Press，1987（in Chinese）

［14］周源泉，翁朝曦.可靠性评定［M］.北京:科学出版社，1990:12－13

Zhou Yuanquan，Weng Zhaoxi.Reliability assessment［M］.Beijing:Science Press，1990:12－13（in Chinese）

Pseudo-life-based test method of mechanism consistency boundary for accelerated degradation testing

Lin Fengchun Wang Qiancheng Chen Yunxia Kang Rui
（School of Reliability and Systems Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

A pseudo-life-based test method of mechanism consistency boundaryforaccelerated degradation testing was proposed，according to mechanism consistency condition for lifetime random variables.Based on the pseudo life estimates，an F statistic was established to test the homogeneity of degradation mechanism characteristic parameters，where the characteristic parameter is logarithm standard deviation for log-normal distribution and shape parameter for Weibull distribution.And the exact rejection region was given.Using the F statistic，mechanism consistency test was done level by level from lower to higher，until the consistency condition was unsatisfied or the pseudo life estimates at all levels had been analyzed.Then，the stress level of mechanism consistency boundary was determined.This method can make good use of the transverse information from the degradation mechanism consistency between different accelerated stress levels，and effectively increase test precision.It has been used to determine the thermal degradation mechanism consistency boundary temperature for a coating flat glass，and the results show the rationality and validity of the presented method.

mechanism consistency;accelerated degradation testing;pseudo life;F test

O 213.2;O 212

A

1001-5965（2012）02-0233-06

2010-10-25;< class="emphasis_bold">网络出版时间:

时间:2012-02-21 11:46;

CNKI:11-2625/V.20120221.1146.016

www.cnki.net/kcms/detail/11.2625.V.20120221.1146.016.html

林逢春（1984－），女，山东临沂人，博士后，现工作在中国空间技术研究院通信卫星事业部，linfengchun@buaa.edu.cn.

（编 辑:娄 嘉）