利用人工势函数法的卫星电磁编队控制

苏建敏 董云峰

（北京航空航天大学 宇航学院，北京 100191）

利用人工势函数法的卫星电磁编队控制

苏建敏 董云峰

（北京航空航天大学 宇航学院，北京 100191）

卫星电磁编队是指利用卫星之间相互作用的电磁力进行卫星相对运动控制，对控制律的要求主要是计算量小和能避免碰撞.以目标星对参考星的相对运动矢量作为控制对象，分析了使用电磁力控制卫星编队的可行性，结果是如果编队卫星磁矩能够任意控制，那么卫星相对运动也能完全控制.设计了人工势函数，以相对位置和相对速度矢量作为变量，人工势函数在达到控制目标时为最小值，在碰撞的位置具有局部最大值.设计的控制律能够实时调整控制参数，能够保证电磁线圈控制电流不至于饱和，以及人工势函数导数在控制过程中小于零.仿真表明，所设计的控制律能生成编队构型并避免碰撞，而且具有一定的抗干扰性.

人工势函数;电磁编队;避免碰撞;饱和;抗干扰

卫星编队是指多颗小卫星在围绕地球运动的同时，彼此之间形成特定的编队构型，共同完成空间任务.电磁编队则是利用安装在卫星上的通电线圈之间的电磁力进行卫星相对运动控制的编队.卫星编队飞行控制主要关心的是卫星的相对运动，对绝对轨道的控制是次要的，因此利用卫星之间相互作用力来进行相对运动控制是对卫星推进系统的一种必然的改进.电磁力推进系统相比较普通推力器的优点在于，不消耗工质，不会有工质耗尽导致编队寿命终结的问题;没有推力器喷气尾流对卫星有效载荷的污染，和对其他卫星的动力学干扰.缺点在于电磁力的作用距离有限，产生电磁力的同时会产生附加力矩，以及强磁场对星上电子设备的干扰.

编队飞行控制策略的研究主要分为2类:从传统的卫星轨道控制出发，以卫星之间轨道根数的差异作为控制目标;以CW方程为主的卫星动力学方程，以卫星相对位置和速度为控制目标，在轨道坐标系下进行控制.文献［1］采用非奇异的轨道根数差来描述相对构型，利用高斯变分方程计算生成对应的轨道根数差所需要的脉冲大小和方向，将结果与数值优化的结果进行了比较.文献［2］对轨道根数差进行数学变换，得到一组新的参数来描述相对构型，并推导相对轨道摄动微分方程，导出脉冲与相对轨道要素变化的关系.文献［3］把卫星相对运动轨迹规划问题，转换成带碰撞约束的燃料最优线性规划问题，并采用混合整数线性规划方法（MILP，Mixed Integer Linear Programming）进行求解.文献［4］提出一种分布式的编队构型生成与重构的规划方法，在考虑碰撞可能性的前提下，通过优化发动机正向推力/停止/反向推力的切换时间来完成规划.文献［5］把碰撞限制下的编队重构问题转化为大量不等式约束的非线性燃料最优问题，并利用平行多重打靶法进行求解.文献［6］以凸优化的方法规划出期望重构机动路径，然后设计基于二阶一致性算法的反馈协同控制律，控制实际位置跟踪期望轨迹，减小了燃料消耗总量，提高了燃料消耗均衡性.

综上，由于星上燃料的宝贵性，以推力器控制的编队控制问题一般转化为燃料最优问题进行求解.

电磁编队的控制是紧耦合的，对一颗星的控制会影响到其他卫星，随着卫星个数的增加，问题的复杂性也会增加，如果采用优化的方法寻找最优轨迹，优化问题的规模会随卫星个数增加扩大而呈几何级数增长，所幸的是电磁编队控制消耗的是可再生的电能，最优控制在此变得不那么重要［7］，而由于电磁力作用范围小，电磁编队卫星彼此的距离很近，卫星可能的碰撞问题在控制过程中需要重点考虑.人工势函数法最早用于机器人控制，它的基本思想是构造一个势函数，该函数在机器人目标位置和目标速度具有全局最小值，在障碍物处具有局部最大值，如果设计控制律使得势函数的导数小于零，就能保证机器人在有限的时间内到达目标位置和目标速度，并有效的避开障碍物［8］.由于人工势函数法不需要进行轨迹规划且能有效防止碰撞，在卫星相对运动控制上也得到了应用，文献［9］把人工势函数法用于空间自主交会对接导航.文献［10］则利用人工势函数法控制理想情况下的电磁卫星编队，其设定的运动环境是二维平面，且卫星不受外力，控制使得卫星的相对位置发生变化，相对速度为零.

由于Ahsun考虑的理想情况与实际的卫星编队运动情况有所差异，本文在其基础上进行了改进，得到的控制律适合三维空间地球重力场中的电磁编队的运动控制，所做的改进主要是通过实时调整控制参数，保证控制的稳定性和控制力可实现.此外本文还对电磁编队的可控性进行了分析.

1 电磁编队可控性分析

由于电磁力的作用是相对的，电磁编队无法对单颗卫星单独施加控制，对一颗卫星施加控制必然影响到另一颗卫星，而对这两颗星的控制又会影响到与其他卫星的相对运动状态，因此首先需要分析电磁编队的可控性，即当电磁编队中卫星上的磁矩能任意取值时，各个卫星之间的相对运动状态是可控的.这一命题可以分为两部分:①如果编队中各个卫星的磁矩可以任意取值，那么各个卫星受到的电磁力也能任意取值;②如果编队各个卫星所受的电磁力能任意取值，那么卫星之间的相对运动状态可控.

假设卫星上正交安装3个电磁线圈以获得任意大小和方向磁矩，其中单个电磁线圈磁矩的大小可表示为

式中，n为线圈匝数;i为线圈电流;a为线圈半径;磁矩μ的方向与线圈电流方向符合右手法则.

设两个卫星的磁矩分别为 μ1和 μ2，卫星2相对于卫星1的位置p，卫星2受到卫星1的作用力 f21为

式中，μ0是真空磁导率，等于4π×10－7N/A2.

设有n颗卫星，编号从1到n，质量分别为m1，…，mn，在近地空间编队飞行，每颗卫星所受的电磁力分别为fei，其他外力分别为fai.以卫星1作为参考星，卫星2到n相对于卫星1的位置和速度矢量分别为pi，vi，以每颗卫星的磁矩μi作为未知量，有以下方程组:

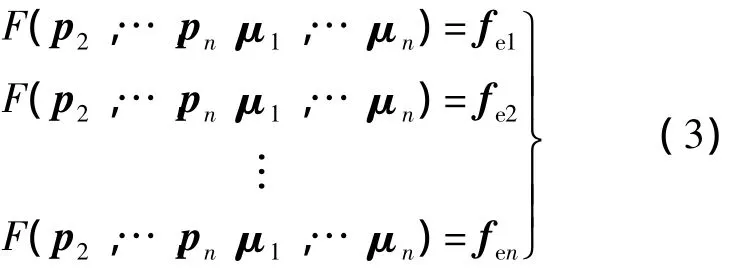
由于电磁力合力为0，方程组（3）包括一个冗余的方程，实际有效的方程个数是n－1.把矢量表示为标量的形式后，方程组的未知量个数为3n，而限制方程的个数为3（n－1），如果磁矩能任意取值，总能满足电磁力的要求.

编队中卫星之间相对运动状态可控，等同于矢量 pi，vi，i=2，3，…，n 完全可控，卫星相对运动方程如下:

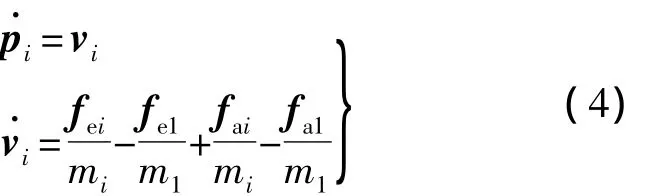
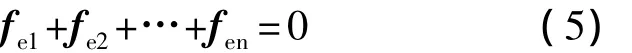
联立式（4）的第2个式子和式（5），以 fe1，fe2，…，fen作为未知量，对于任意给定的，可以求出满足要求的电磁力.即如果编队各个卫星所受的电磁力能任意取值，那么能任意取值，卫星之间的相对运动状态可控.

2 用人工势函数法的电磁卫星控制

沿用上一节的定义，编号从1到n的n颗卫星，以1星作为参考星，其他星相对于参考星的位置和速度分别为 pi和 vi，i=2，3，…，n，目标相对位置和速度记为pi0和vi0，设计势函数使得编队中的卫星在目标相对位置和速度具有全局极小值:

为了避免编队卫星在达到目标相对位置和速度的过程中发生碰撞，在函数中加入一项以防止碰撞发生，该项在碰撞发生时具有局部极大值:

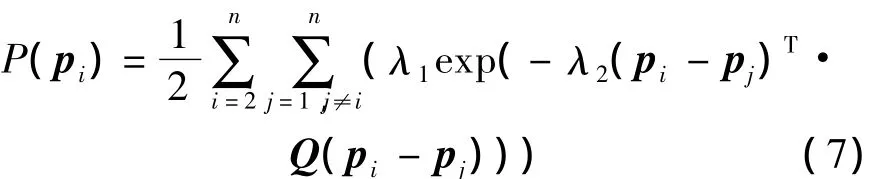
式中，p1为0;λ1，λ2是正常数;Q为正对角矩阵.

联立式（6）和式（7），得到势函数V:

对势函数V求导得:

根据梯度函数ΔOij的性Δ质:

对式（9）进行整理得到

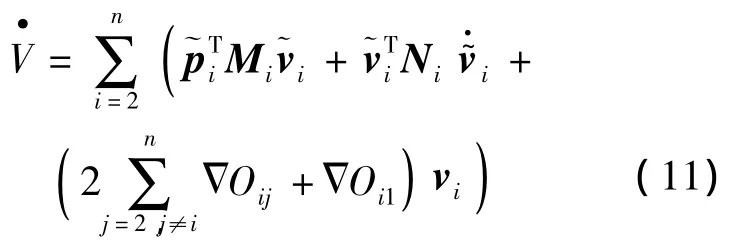
设计控制律:本文Ki是正对角矩阵.

式（12）代入式（11）得势函数的梯度为

ΔOij是防碰撞势函数的梯度函数，当卫星之间距离越近，其值越大，而在目标状态，取值趋近零.vi0为第i颗卫星的目标相对速度，取值随时间在一定范围内周期性变化.为了保证式（13）为负值，需要控制Ki的取值.

电磁线圈产生的电磁控制力是有限的，当正交安装的3个电磁线圈其中一个的电流发生饱和时，如果像文献［10］那样简单进行限幅，那么实际产生的磁矩大小和方向均与预计的不符，最终每颗卫星受到的控制力可能与要求的控制力相差很多，所以在控制律的设计中必须尽量保证电磁线圈不至于发生电流饱和.为了实现这一目的，对控制量进行限制，由于电磁力大小与磁矩乘积成正比，与距离四次方成反比，因此给设定一个阀值，dmax为卫星之间最大距离，通过调整Ni的大小来保证小于给定的阀值.确定控制量的算法是:i从2到n.

关于控制磁矩的方程组（3），直接利用数值方法迭代求解，具体可采用“Matlab”的“fsolve”函数.电磁线圈在产生控制力的同时也会产生附加力矩，包括电磁线圈之间的电磁力矩和地球磁场对电磁线圈作用的电磁力矩，用动量轮进行吸收以维持卫星姿态的稳定.

3 仿真研究

包括4颗星的电磁编队进行构型初始化，轨道为圆轨道，目标构型为能自然稳定的空间椭圆，4颗星相对于其中心的目标轨迹如下:

式中，θi为卫星的相位，分别为 0，π/2，π，3π/2;ω是轨道角速度.

初始时刻卫星 1的轨道根数为（7000 km 0 30° 0 0 0），因为构型初始化在短时间内完成，摄动力模型仅考虑地球J2项.电磁线圈所能产生的最大磁矩μ与线圈质量m、线圈半径a和线圈超导材料的性质Ic/ρc的关系如下:

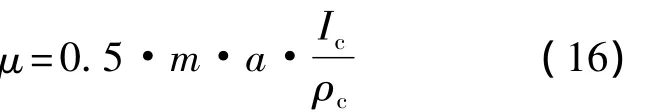
式中，Ic为单位截面积的超导材料能通过的最大电 流;ρc为 材 料 密 度;Ic/ρc的 取 值 为16250 Am/kg［7］.仿真参数如表 1 所示.

表1 仿真参数表

在文献［10］中，卫星从静止到静止的控制过程中，会碰到“停止点”，原因是势函数的第1部分（式（6））的导数，与势函数的防碰撞部分（式（7））的导数相互抵消，导致还没有达到目标位置的时候，控制力为零.而在运动到运动的控制过程中，即使卫星在某处“停止”了，由于目标位置随时间变化，势函数第1部分的导数的方向也会随时间变化，与势函数防碰撞部分的导数也会不同，以致重新产生控制力离开“停止”点.假设卫星初始相对位置如下:xi（0）=－0.5xi0（0）;yi（0）=－0.5yi0（0）;zi（0）= －0.5zi0（0）.

构型生成过程中卫星的相对运动轨迹如图1所示，图1包括了一个三维视图和3个侧视图，坐标原点为卫星群几何中心，能清楚的看出卫星在达到目标轨迹的过程中为避免碰撞所做的机动.图2是控制过程中4颗卫星之间的距离，可知卫星之间的最小距离大于5 m.

与控制误差相关的因素是:控制力的误差、卫星受到摄动力和相对状态的观测误差，表2给出了这些误差因素在仿真中的设置.

仿真结果中控制误差曲线如图3所示.

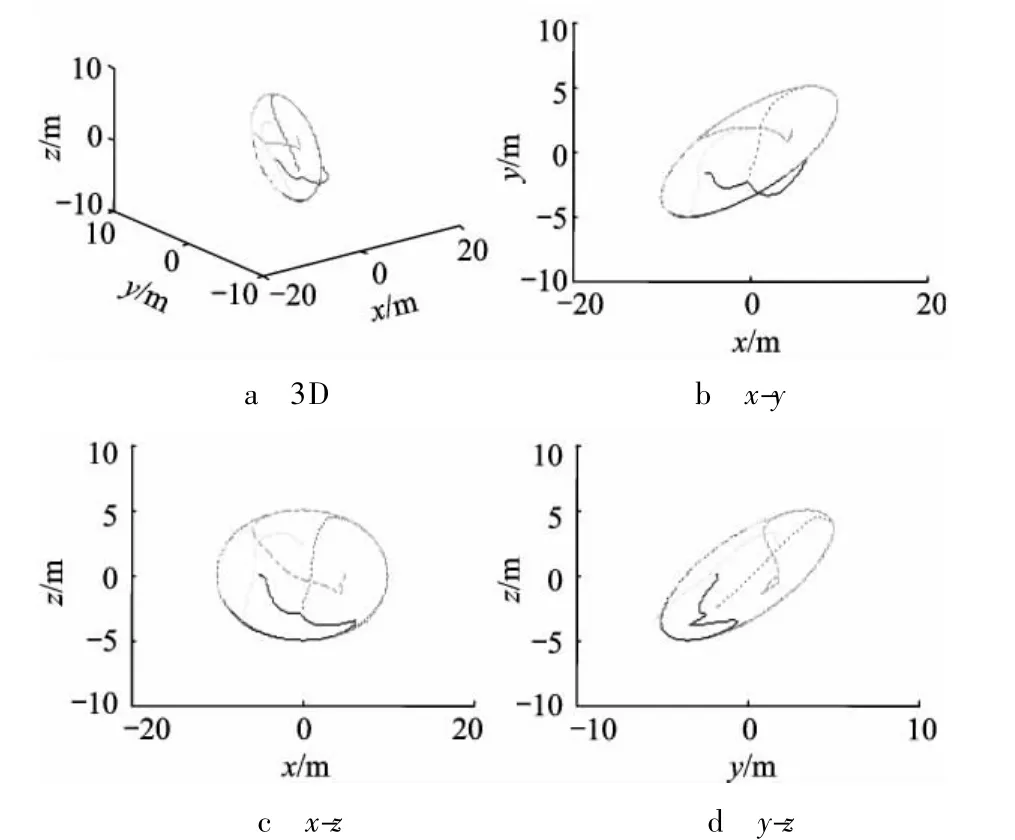
图1 相对运动轨迹

图2 卫星之间相对距离

表2 与误差相关的因素

图3 相对状态的控制误差

最终位置误差为10－1m量级，速度误差为10－3m/s量级，误差曲线有较明显的毛刺现象，原因在于仿真中未对测量数据进行平滑处理.

仿真的其他结果如图4～图6所示.

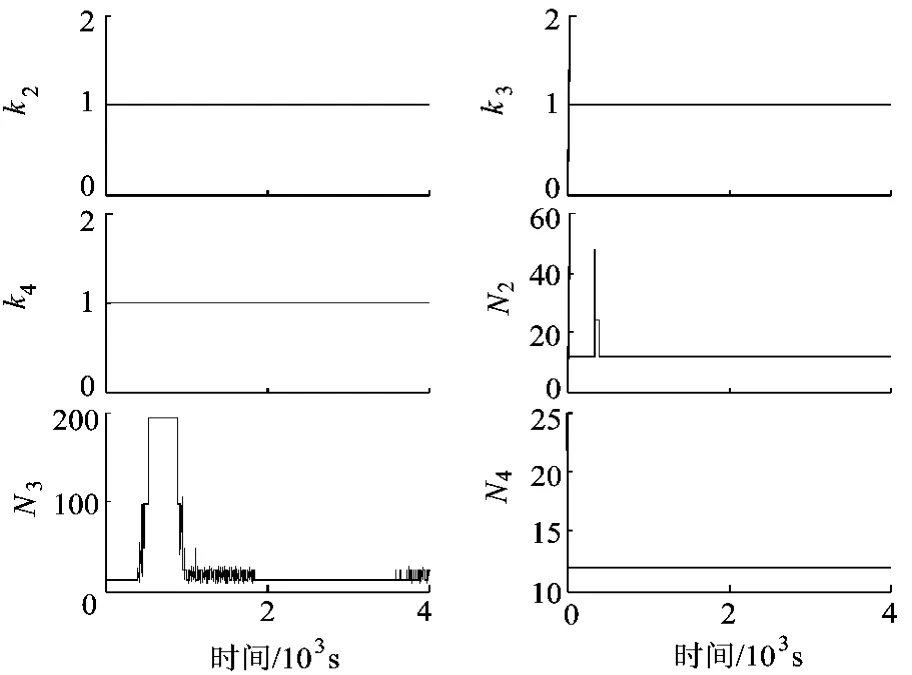
图4 控制系数

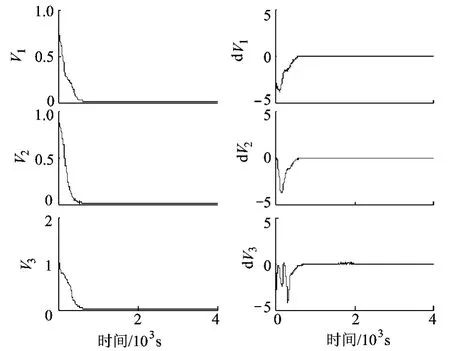
图5 势函数与势函数导数

图6 控制磁矩

图4给出了控制过程中控制系数的变化，为了简便起见，用矩阵N，K的第1个元素的值代表这个矩阵.通过实时调整控制系数，达到了两个目的，从图5和图6可以看出，首先是势函数的导数小于0，保证了能稳定收敛到目标状态，然后是卫星磁矩都在可实现范围之内.

4 结论

通过把电磁编队的相对运动控制分解成对多个相对运动状态矢量的控制，构造了人工势函数，并推导控制律，对编队构型生成进行了仿真研究，得到了有意义的结论.

如果编队中的卫星磁矩完全可控，那么编队卫星的相对运动状态也完全可控.仿真表明，编队卫星在构型生成的过程中做了种种规避动作以避免可能的碰撞，基于人工势函数法设计的控制律达到了防止碰撞的目的.在考虑了观测误差，执行误差以及摄动力的情况下，编队仍然在控制力的作用下完成构型生成，说明人工势函数控制律具有一定的抗干扰性.对控制系数的实时调整保证了电磁线圈不至于处于电流饱和状态，不会因为电流饱和而影响控制效果.

（References）

［1］Vaddi S S，Alfriend K T，Vadali S R.Formation establishment and reconfiguration using impulsive control［J］.Journal of Guidance，Control，and Dynamics，2005，28（2）:262－268

［2］He Q，Han C.Dynamics and control of satellite formation flying based on relative orbit elements［C］//AIAA Guidance，Navigation and Control Conference and Exhibit.Honolulu:AIAA，2008

［3］Richards A，Schouwenaars T，How J P.Spacecraft trajectory planning with avoidance constraints using mixed-integer linear programming［J］.Journal of Guidance，Control，and Dynamics，2002，25（4）:755－764

［4］Campbell M E.Planning algorithm for multiple satellite clusters［J］.Journal of Guidance，Control，and Dynamics，2003，26（5）:700－780

［5］Massari M，Zazzera F.Optimization of low-thrust reconfiguration maneuvers for spacecraft flying in formation［J］.Journal of Guidance，Control，and Dynamics，2009，32（5）:1629－1638

［6］张博，罗建军，袁建平.一种基于信息一致性的卫星编队协同控制策略［J］.航空学报，2010，31（5）:1004－1013

Zhang Bo，Luo Jianjun，Yuan Jianping.A satellite formation cooperative control strategy based on information consensus［J］.Acta Aeronautica et Astronautica Sinica，2010，31（5）:1004 －1013（in Chinese）

［7］Kong E，Kwon D，Schweighart S，et al.Electromagnetic formation flight for multisatellite arrays［J］.Journal of Spacecraft and Rockets，2004，41（4）:659－666

［8］Khatib O.Real-time obstacle avoidance for manipulators and mobile robots［J］.The International Journal of Robotics Research，1986，5（1）:90－98

［9］Martinson N.A new method of guidance control for autonomous rendezvous in a cluttered space environment［C］//AIAA Guidance，Navigation，and Control Conference.South Carolina:AIAA，2007:602－610

［10］Ahsun U，Miller D.Dynamics and control of electromagnetic satellite formations［D］.Massachusetts:Department of Aeronautical and Astronautical Engineering，Massachusetts Institute of Technology，2007

Artificial potential function method for satellite electromagnetic formation control

Su Jianmin Dong Yunfeng
（School of Astronautics，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

The relative motion of electromagnetic satellites is activated by electromagnetic force between satellites.The control law should satisfy two conditions，low calculation burden and ability of avoiding collision.The control objects are relative motion vectors of satellites to reference satellite.The analysis of feasibility of electromagnetic force control to satellite formation shows that relative motion of satellites can be controlled if electromagnetic strengths of satellites can be controlled.An artificial potential function was designed.Relative positions and relative velocities are treated as variables.The value of the function is minimal when control object is got，and it is local maximal when collision happens.By regulating control parameters in real time，which the current of electromagnetic coils won't beyond upper limit is regarded.The derivative of artificial potential function is less than zeros in control process.Simulation shows that electromagnetic satellites configuration would be generated when control law was imposed with interference.

artificial potential function;electromagnetic formation;collision avoidance;saturation;anti-interference

V 412.4

A

1001-5965（2012）02-0213-05

2010-10-11;< class="emphasis_bold">网络出版时间:

时间:2012-02-21 11:46;

CNKI:11-2625/V.20120221.1146.019

www.cnki.net/kcms/detail/11.2625.V.20120221.1146.019.html

苏建敏（1982－），男，湖北仙桃人，博士生，jackysura@gmail.com.

（编 辑:张 嵘）