浮空气囊定常及非定常气动特性计算

宋书恒 陈德华 刘晓波

(中国空气动力研究与发展中心，绵阳621000)

以气囊为主体结构的飞行器在军事和民用方面具有广泛的应用范围［1－4］，如飞艇、热气球等，与其它飞行器相比，该类飞行器具有如下特点和优点:可垂直起降、空中悬停，噪音低、污染小和长滞空时间，可全天候、超低空和超高空飞行，成本较低，用途广泛等.而随着新的应用领域的开发，如临近空间［5］，该类飞行器再一次成为研究的热点.

浮空类飞行器是一种以静升力为主的飞行器，所以其气囊结构一般容积较大，且多为旋成体，在运行过程中外形有可能发生变化，这就导致了其流场具有不同于其它飞行器的特点.并且由于运行空域较广，流场参数变化复杂，或出于姿态控制的需要，非定常气动特性对其也有着非常重要的意义.本文采用数值模拟方法研究了较广空域范围内浮空气囊的气动特性，计算模型包括0～20km范围内5个不同高度下不同外形的气囊，对其定常和非定常气动力和流动分离特性进行了计算与分析.计算结果表明，随着高度与气囊外形的变化，其气动力与流动分离模式差别较大，并且气囊的非定常运动对其流场和气动力有较大影响.

1 数值方法

1.1 控制方程及求解

本文的流动控制方程是三维非定常不可压缩N-S(Navier-Stokes)方程，采用虚拟压缩的思想［6］，在连续性方程和动量方程中分别引入压力和速度对虚拟时间的导数项，然后变换至一般曲线坐标系下求解.方程中的对流通量项采用基于 Roe的近似 Riemann 解的三阶迎风格式［7－8］，粘性项采用二阶中心差分，离散后方程采用双时间步方法及 LU-SGS［7－8］格式求解，湍流模型采用B-L代数模型.

1.2 计算方法验证

为了验证数值方法和网格的可靠性，首先选取具有实验结果的算例进行对比计算［9］，得到了比较满意的结果.验证算例是一个6∶1的椭球，图1是计算网格示意图，考虑流场对称的情况，计算时采用半模模型，2套网格规模分别为49×43×41(轴向、周向、法向)和73×49×49，网格在物面附近加密.

图2是某状态下椭球某轴向位置处的表面压力系数沿周向的分布与实验的比较，可见它们均与实验值符合得较好，证明了计算方法和网格的有效性.2种网格的计算结果差别不大，故本文后面的计算采用第1套网格.

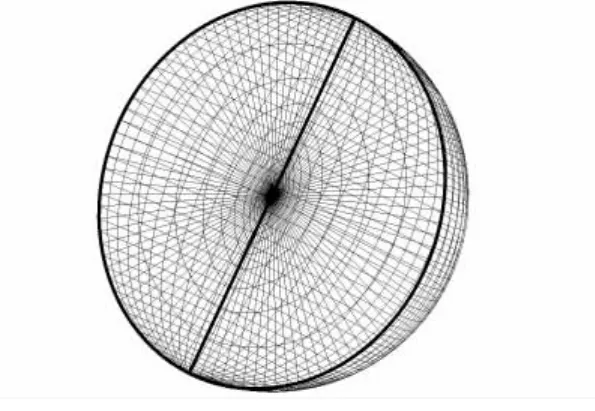
图1 椭球计算网格

本文中不同外形的气囊，所采用的网格拓扑结构和规模与上述椭球的网格完全一致.本文的计算模型是5个不同高度下的气囊，均为旋成体.图3给出了不同高度下气囊的型面曲线.对于气囊的非定常流场计算，运用刚性运动网格技术.

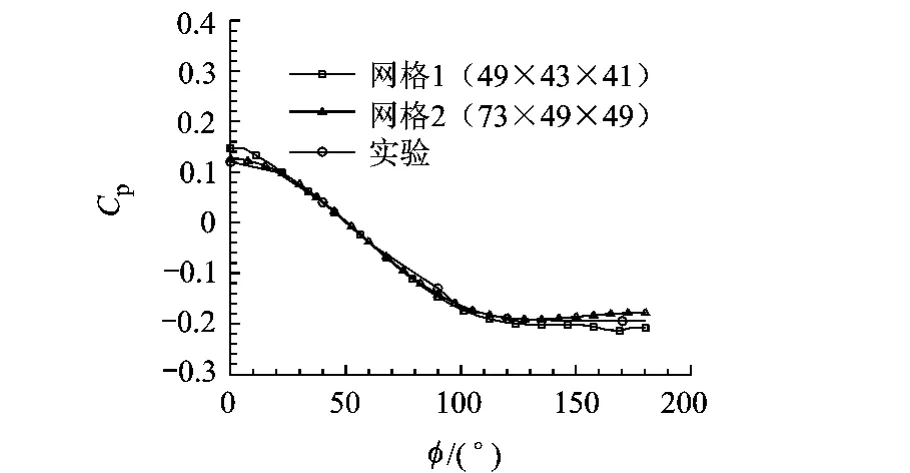
图2 椭球某轴向位置表面压力系数随周向角度的变化

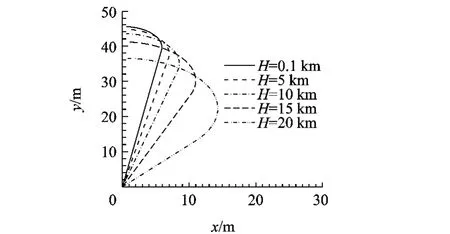
图3 不同高度时气囊外形型面曲线

2 计算结果及分析

基于上述数值方法和网格，首先对不同高度及多个攻角状态下浮空气囊的定常流场进行计算，而非定常流场选取了高度为10 km时的气囊进行计算，其运动模式包括平移和俯仰2种情况.对囊体的表面压力分布、流动分离、气动力变化特性作出了分析.

2.1 不同高度下气囊定常气动特性

首先对不同高度下气囊的定常流场进行计算，每一个高度时攻角分别为 －10°， －5°，0°，5°，10°，流场计算参数采用相应高度的标准大气参数.

图4给出了H=10 km时各攻角 (α)状态下气囊表面的压力分布与极限流线，其压力分布的规律是:在气囊的迎风区与背风区形成了较明显的高压区域，在前缘迎风区，高压区自顶部至底部几乎覆盖整个气囊，而在自前缘起沿周向辐角约为90°的区域附近形成了一个明显的低压区.随着攻角的增大，该低压区逐渐变得狭长.同时可以看出，在气囊的背风区，存在较强的流动分离，分离区基本都位于气囊背风区底部.而随攻角的增大，分离区逐渐向上扩展.

随着高度增加，在某些状态下，气囊背风区顶部也会出现流动分离，局部将会发生二次流动分离.H=20km时，气囊的轴向长度最小，而横向最大截面面积最大，即厚度率最大.此时，在背风区的大部分区域，均存在严重的流动分离，随攻角增大，背风区顶部分离区逐渐向前延伸.图5给出了其空间流线.可以看出，在其背风区顶部、中部及底部都出现了大尺度的流动分离.

图4 不同攻角时气囊表面极限流线及压力云图

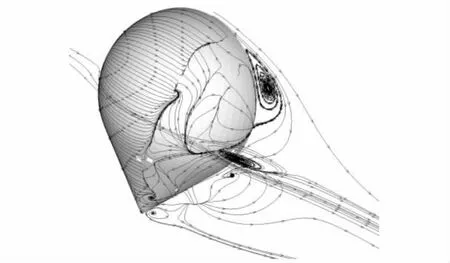
图5 气囊空间流动分离图

图6是不同高度下气囊的升阻力随攻角的变化情况.对于不同的气囊，其升阻力基本随攻角增大而减小，在H=10km时，升阻力变化不明显.

2.2 平移运动气囊的非定常气动特性

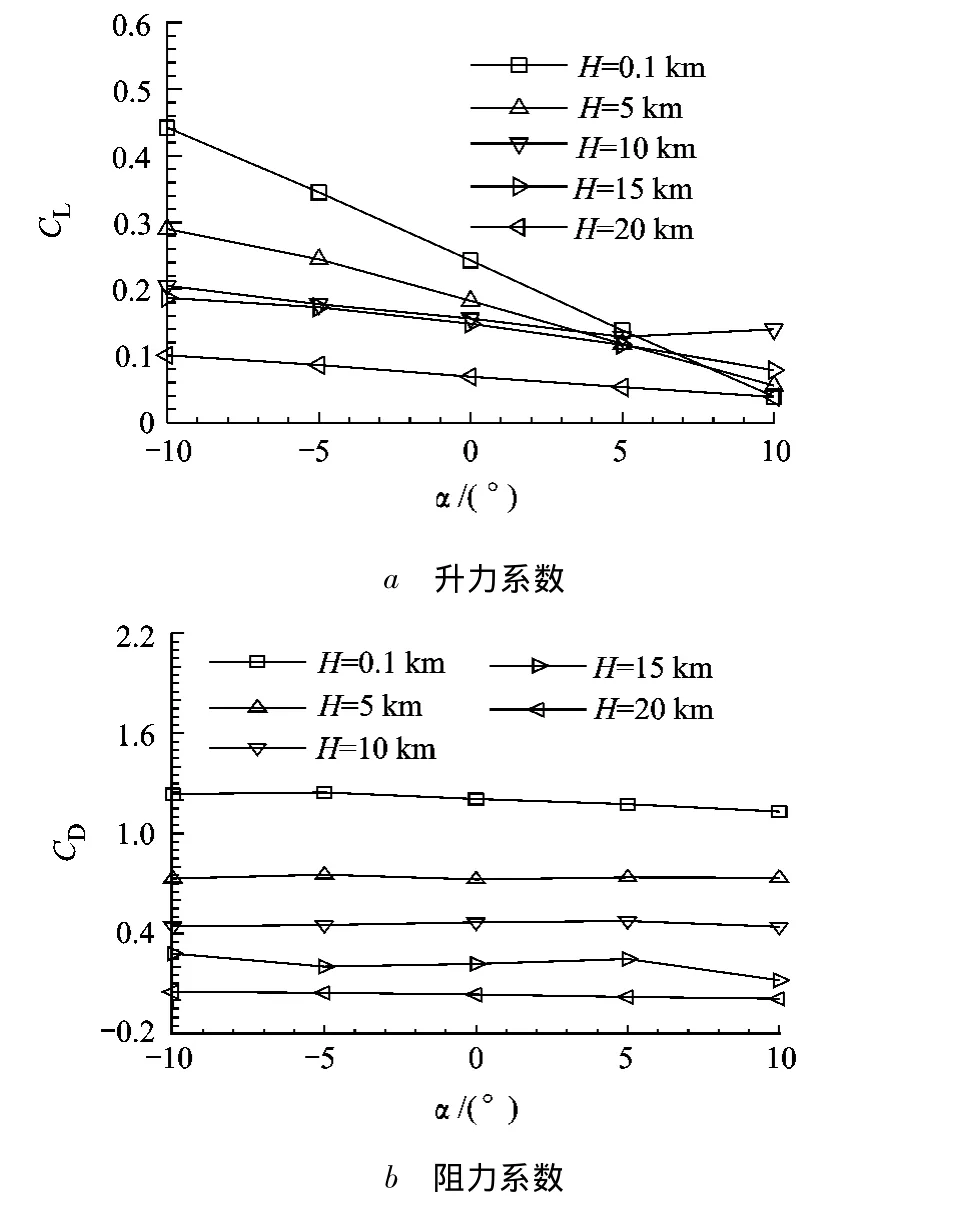
图6 气囊气动力曲线

浮空气囊在运行的过程中，由于运行区域流动参数的复杂多变或出于控制的需要，有可能进行非定常运动.本文对浮空气囊平移运动时的非定常流场进行了计算，以高度为10 km时的气囊为例，考虑了顺风和逆风平移2种运动状态，考察了运动速度和方向对气囊气动力及流动分离的影响.所有的非定常计算均从定常状态时的稳定流场开始，计算参数见表1.

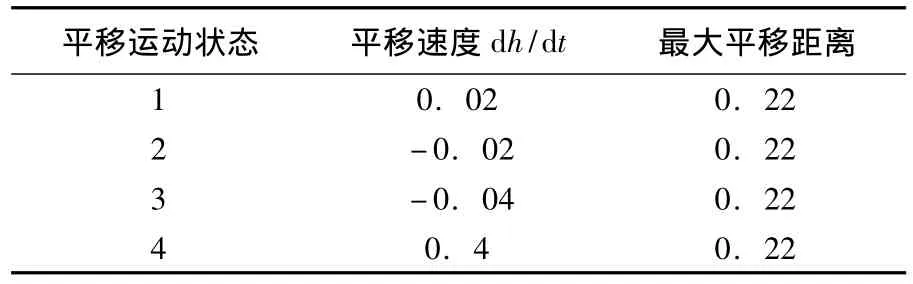
表1 平移运动气囊计算参数表

图7是平移运动气囊的表面压力分布与极限流线，分别给出了气囊运动至2个不同位置时的结果.平移速度dh/dt=0.02时，囊体顺风平移，当平移距离较小时，表面压力分布及流线与定常时相比无明显区别;而当平移距离较大时，表面低压区范围略有减小，背风区流动分离范围扩大，且在囊体顶部附近出现明显分离区.结果表明，当 dh/dt=－0.02及 dh/dt=－0.04时，气囊表面的压力分布及流线与上述情况类似.当dh/dt=0.4时，平移速度较大，囊体表面压力分布及流线变化也较大，前缘迎风区无明显高压区，整个囊体表面压力较高，背风区流动分离范围显著减小.

图8是气囊在不同的平移速度下气动力系数的变化情况.当平移速度较小时，无论是顺风或逆风运动，升力系数随平移距离的增加而增大，阻力系数变化不明显.当囊体以较高速度顺风平移时，则会对囊体产生一个反方向的推力.俯仰力矩的变化情况是:当逆风平移时，在运动过程中，力矩逐渐由负变正;当顺风平移时，将产生一个负的力矩，平移速度较大时，力矩的值较大.

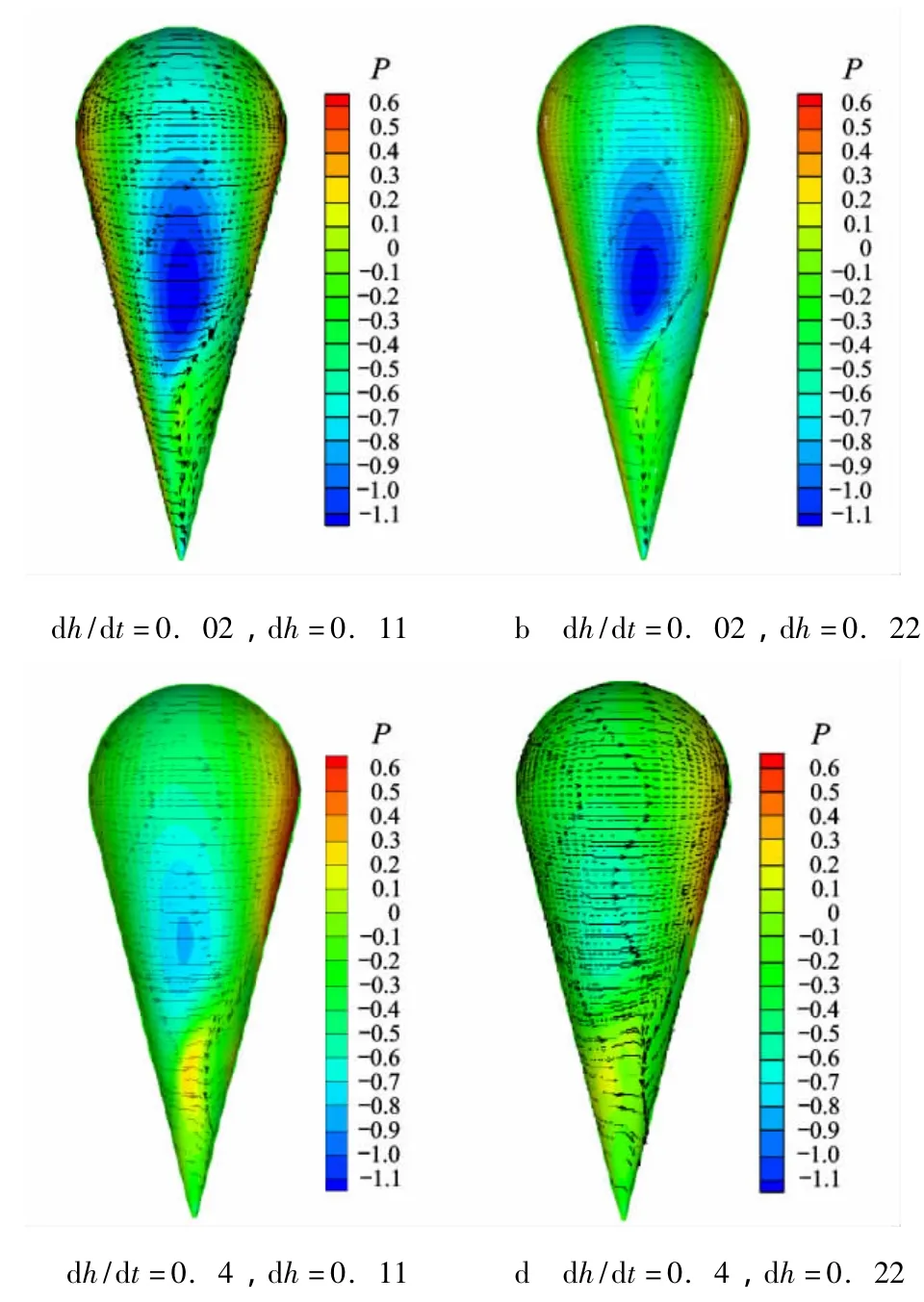
图7 平移运动气囊极限流线及压力云图

2.3 俯仰运动气囊的非定常气动特性

有关气囊的俯仰运动，这里同样选取了H=10 km时的外形，相关的计算参数见表2.

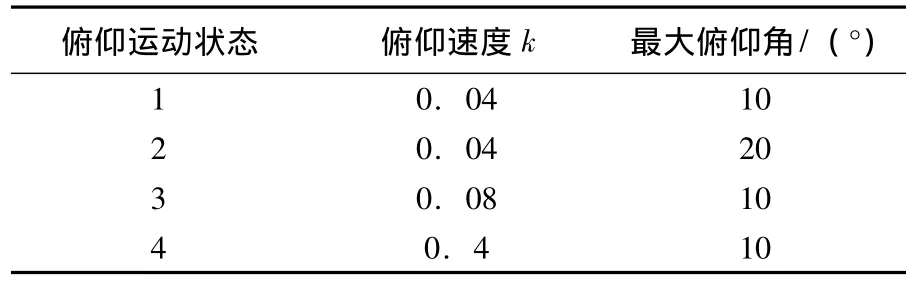
表2 俯仰运动气囊计算参数表

图9是H=10km时气囊表面的压力分布与极限流线.当气囊以较低速度作俯仰运动时，随着攻角的增大，背风区分离区随之扩大，表面低压区范围变小，而俯仰速度较高时，背风区分离区扩大不明显.

图10是对应的气动力系数.低俯仰速度时，升力系数随攻角增大在一定的攻角范围内呈线性增加，然后急剧下降，阻力随攻角增加而增大，运动过程中产生一个低头力矩，随攻角增加先减小后增大.高俯仰速度时，随着攻角的增大，升力减小，阻力及力矩增大，相对低俯仰速度而言，阻力较小而力矩较大.

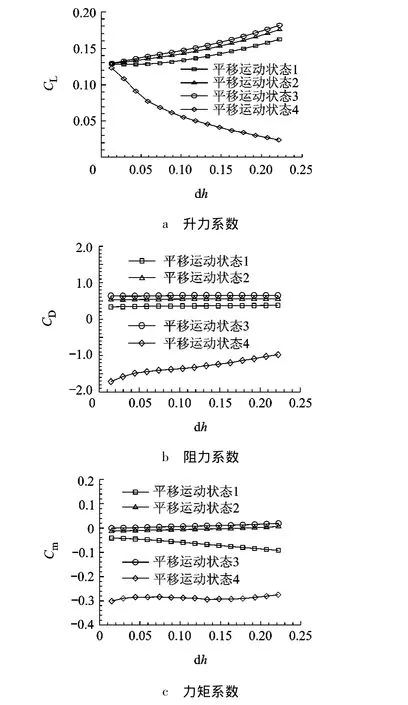
图8 平移运动气囊气动力随位置变化

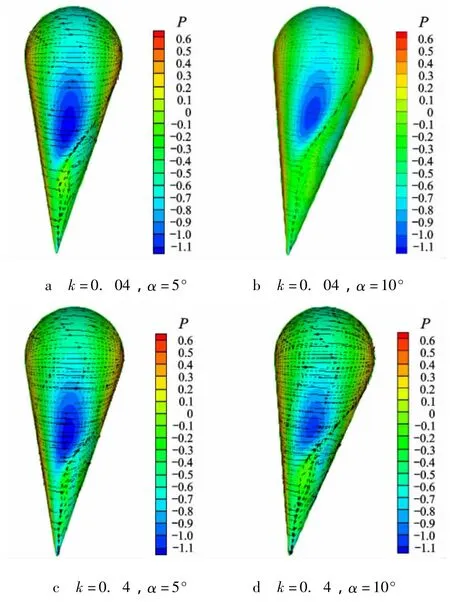
图9 俯仰运动气囊极限流线及压力云图

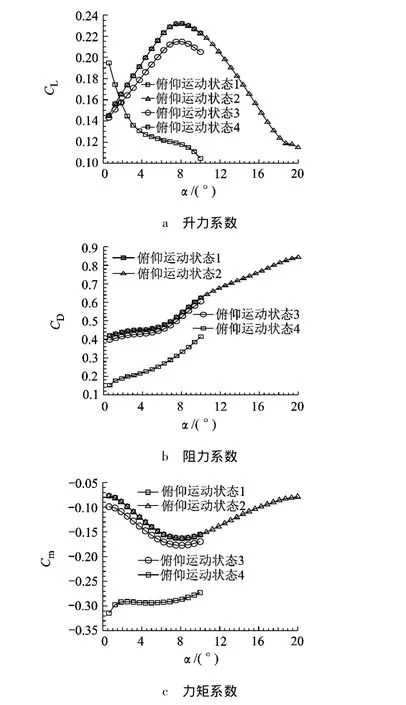
图10 俯仰运动气囊气动力随攻角变化曲线

3 结论

对于浮空气囊的定常流动，不同高度时，因气囊外形及流动参数的变化，其表面压力分布、气动力及流动分离模式差别较大.当浮空气囊进行非定常运动时，非定常运动模式及其速度大小对气囊的流场与气动力影响显著.气囊以较小速度平移时，无论是顺风或逆风，气动力及流动分离变化不明显;较大速度顺风平移时，气囊的表面压力分布、气动力及流动分离显著改变.对于气囊的俯仰运动，较小速度俯仰时，气囊背风区分离明显扩大;较大速度俯仰时，气动力的变化趋势显著不同.

References)

［1］Khoury G A，Gillett J D.Airship technology［M］.New York:Cambridge University，1999

［2］甘晓华，郭颖.飞艇技术概论［M］.北京:国防工业出版社，2005

Gan Xiaohua，Guo Ying. Introduction to airship technology［M］.Beijing:National Defense Industry Press，2005(in Chinese)

［3］Schafer Ingolf.Airships as unmanned platforms-challenge and chance［R］.AIAA-2002-5882，2002

［4］Harada Masashi，Sano Masaaki.Theoretical analysis of a new design concept for LTA structure［R］.AIAA-2002-3425，2002

［5］李怡勇，李智，沈怀荣.临近空间飞行器发展与应用分析［J］.装备指挥技术学院学报，2008，19(2):61－65

Li Yiyong，Li Zhi，Shen Huairong.Analysis on development and application of near space vehicle［J］.Journal of the Academy of Equipment Command＆ Technology，2008，19(2):61－65(in Chinese)

［6］Rogers S E.Numerical solution of the incompressible Navier-Stokes equations［R］. NASA TechnicalMemorandum 102199，1990

［7］Rogers S E，Kwak D，Kiris C.Steady and unsteady solutions of the incompressible Navier-Stokes equations［J］.AIAA Journal，1991，29:603 －610

［8］宋书恒.微型飞行器相关气动力特性的数值模拟［D］.绵阳:中国空气动力研究与发展中心研究生部，2007

Song Shuheng.Numerical simulation of aerodynamic characteristics for micro air vehicles［D］.Mianyang:Graduate School，China Aerodynamics Research and Development Center，2007(in Chinese)

［9］Hoang N T，Wetzel T G.Surface pressure measurements over a 6∶1 prolate spheroid undergoing time-dependent maneuvers［R］.AIAA-94-1908，1994