各向同性湍流能量级串中的旋涡分岔机制

冉 政

(上海大学上海市应用数学和力学研究所，上海200072)

尽管有关湍流的理论研究十分复杂，进展缓慢［1－2］，但没有人否定湍流研究的重要性.本文选取湍流研究中的能量级串问题，作为主要的关注对象，试图分析湍流能量级串这一概念的起源和演化，以及目前的发展状况.简单地讲，湍流的多尺度和湍流的能量级串 (cascade)是湍流研究中一个十分重要的概念，由于非线性相互作用，湍流中存在尺度之间的逐级能量传递，一般是大尺度旋涡向小尺度旋涡输送能量.然而，这一简单的物理图象却蕴涵十分令人困惑的数学物理问题，它一直是湍流理论研究的核心问题.在湍流研究发展过程，包括 Taylor，Richardson，Kolmogorov，Mandelbrot，Frisch等许多科学家均对此问题做出过贡献，但是，到目前为止，基于第一原理的认识却一直没有实质性的进展.本文在简单阐述这些工作后，介绍了最近的一个理论进展.

1 Richardson能量级串的唯象分析

湍流能量级串的概念起源于Richardson一首广为流传的诗［3］，诗中并无精确的数学物理内容，但却存在清晰的物理图象:在能量级串过程中，第1级大涡的能量来自外界，大涡失稳后，产生第2级小涡，小涡失稳后又产生更小的旋涡，最后，由于Re数非常大，所有可能尺度的运动模式都被激发.Richardson的湍流级串图象已经影响了湍流理论和实验工作者几十年.1941年，Kolmogorov对于湍流的刻画［4］实际上已经使用了这一物理图象.Richardson的湍流级串图象引入了如下的思想:在湍流场中，能量从大尺度向小尺度的传输中，要经历多步的离散过程，这一过程与旋涡的拉伸变形相关联.这种图象自然涉及到一系列的旋涡层次结构以及分岔过程.其中最基本的是认为级串是一个多步过程，这就涉及到不同旋涡尺度的层次结构，一般可以简单地想象为不同直径的球形旋涡组成的层次结构.长期以来，这一过程仅在唯象的分析中得到了部分的理解，而目前的研究表明:Richardson的湍流级串图象具有一定合理的物理性质.但是，由此带来了一系列基本理论问题:①是否存在内在的自然过程导致能量从大尺度旋涡到小尺度旋涡传输;②为什么湍流的能量级串必须是一个多步离散的过程.

2 Kolmogorov湍流理论

Kolmogorov［4］是 第 一 个 用 数 学 公 式 表 述Richardson湍流能量级串图象的学者，他认为:在Re数很大时，湍流可以看成由相差很大的、各种不同尺度旋涡组成，最大的旋涡直接由平均流动的不稳定性或边界条件产生.类似Richardson湍流能量级串图象，这些大尺度旋涡又将破裂成较小的旋涡，较小的旋涡又分岔成更小的旋涡，这样就形成了一串无穷多级的大大小小的旋涡.与Richardson不同的是，Kolmogorov关注的是小尺度湍流的各向同性统计特性，他认为这种湍流统计特性具有一定的普适性.最为主要的思想是:在高Re数条件下，大尺度旋涡级串到小尺度旋涡的过程要经过许多级，以致到惯性区非各向同性的大尺度的影响可以忽略，而认为湍流小尺度是局部各向同性的，并且此时湍流的统计特征与粘性无关，而主要取决于湍流的平均能量耗散.Kolmogorov使用量纲分析的方法得到了两条定律，这实际上可以看成目前湍流理论研究的主要成就.

Kolmogorov理论的主要问题在于没有直接与流体运动方程建立联系，没有动力学基础，同时没有计及湍流间歇性的影响，在之后的文献［5］中，湍流的间歇性得到了一定的刻画，但是第一原理的问题依然没有解决.

3 湍流能量级串的唯象模型

1949 年 Batchelor和 Townsend［6］在实验中发现了湍流小尺度结构的间歇性质，在最初的研究中主要是有关湍流能量耗散率的刻画.这一问题的深入研究最终导致了使用多重分形结构刻画湍流，这是现代湍流研究极其重要的一步，多重分形结构实质表明各向同性湍流是具有动力学结构的系综.1962 年，Kolmogorov［5］和 Obukhov［7］分别提出有关湍流耗散率的对数正则分布模型，Novikov［8］和 Mandelbrot［9］探讨了对数正则模型的内在问题.另外一种多步间歇湍流模型则是1964 年由 Novikov和 Stewart［10］提出的.1974 年，Mandelbrot［11］引入了分形几何的概念，用于理解上述模型的特征，这是该领域的一个重要进展.1974年，Kraichnan［12］分析了在广义自相似意义下湍流能量级串的物理内涵.在湍流学术界影响比较大的是β-模型［13］，这一唯象模型在描述湍流多重分形特性方面较为成功.

值得注意的是，上述的模型实质上属于唯象性质的模型，缺乏动力学支持［13］.

4 湍流能量级串的低维动力学模型

自1963年Lorenz［14］的开创工作以来，非线性动力学系统混沌的研究发展迅速，极大地刺激了湍流理论研究的发展.非线性动力学系统混沌的研究提供了一种革命性的新观点和新方法，如何应用这一新观点和新方法充分发展湍流研究一直是湍流学术界的挑战［15］.多年来，许多学者提出了一些具有完全发展湍流特征的混沌动力学模型，尽管这些模型能够再现一些N-S(Navier-Stokes)湍流的本质特征，但仍属于简化模型，因此属于唯象模型，可以归纳为湍流的低维动力学模型范畴.最为著名的是 Burgers方程模型［16］，它可以看成是N-S方程的一维简化模型，但是它的解不是混沌的，Kolmogorov能谱律也不成立.由 Desnyansky 和 Novikov［17］，以及 Kerr和Siggia［18］，Gloaguen［19］等人提出的壳模型虽然得到了Kolmogorov能谱律，但作为运动方程的定态解，对应相空间中的固定点.中国学者钱俭［20］在1988年也提出一个简化的湍流级串模型，虽然该模型的相空间维度仅为20，但能模拟充分发展湍流的主要特征，包括Kolmogorov能谱，相比之下，该模型能更好地模拟湍流的动力学特征和统计特征.

在湍流能谱空间，上述所有模型均未提供湍流的大尺度动力学的任何信息，这是除有限截断外，最为主要的理论缺陷，另外，上述的模型对于湍流多尺度结构的起源也没有对应的动力学支持，大多数在谱空间讨论.一个自然而然的问题是:能否在湍流方程中存在一个自然的动力系统结构，对湍流级串进行更为理性的 (基于第一原理)刻画.有关各向同性湍流Karman-Howarth方程的精确解的进展［21－24］部分回答了上述问题.

5 各向同性湍流的映射动力系统

出发方程是三维不可压缩流体的Karman-Howarth方程

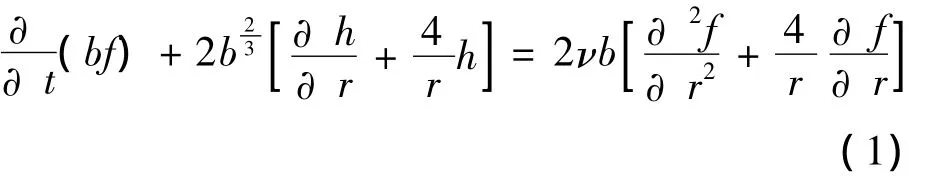
式 (1)不封闭，需要引入一定的封闭条件.采用Sedov提出的封闭方法，可以证明存在以下湍流空间尺度自封闭的演化方程［21－24］:

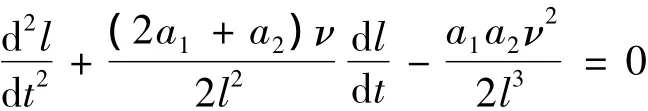
其中a1，a2为两个积分常数.这是一个第二类非线性Lienard型方程，并且可以按标准方法得到精确解.研究以下形式解 (幂次解)，这两类解为

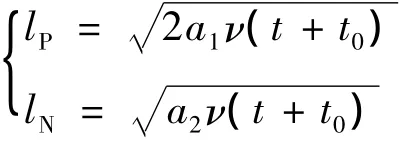
在满足大波数情况的幂次能谱条件下，可以证明所设的湍流参数必须是离散值

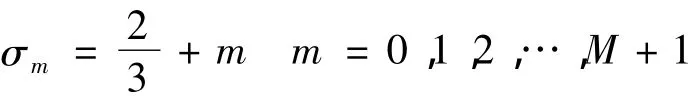
为了有效地度量旋涡系统尺度，必须选择一定的参考尺度，一旦选定参考尺度，其他量与参考尺度做比例，则可以得到对应的度量.本文得到了两种不同的旋涡尺度，如果选择的参考尺度为

由式 (2)可知，lm是递减函数，结合到湍流场中旋涡尺度的范围 (L是湍流外尺度，η是湍流内尺度)L＞lm＞η，则在湍流流场中存在一个递减的旋涡谱系:

完全按照上述思路，如选取测量的尺度是

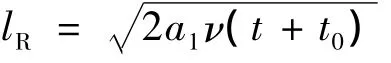
利用两种递增和递减的旋涡谱系，可以建立对应的尺度递推关系.

注意到两点的边界条件，可得如下线性方程组:

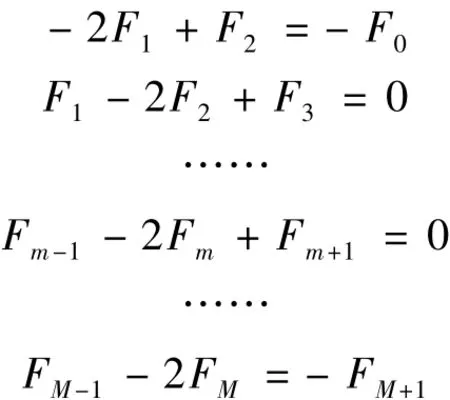
其解可以写为

代入有关的定义，有:

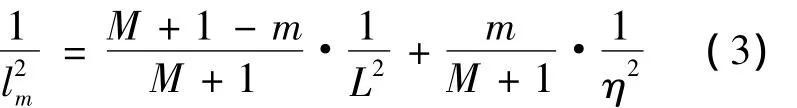
同理有

式 (4)减去式 (3)，有

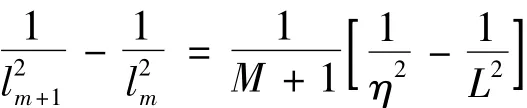
同样的方法可以得到第二特征尺度对应的一个新的递推公式

简单的计算如下:

如果引入条件:A≪1，则可以有近似关系:

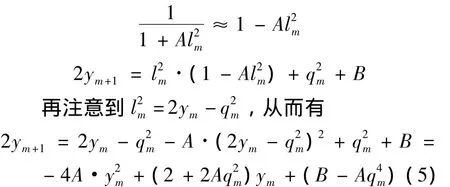
可以证明:各向同性湍流系统的旋涡尺度动力系统拓扑等价如下标准Logistic映射:

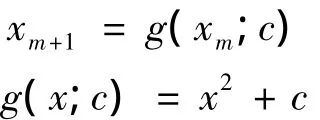
由上述分析可以得到:根据本文新得到的各向同性湍流尺度演化方程，在各向同性湍流系统中存在以湍流Taylor微尺度为动力学量的非线性动力系统

其中

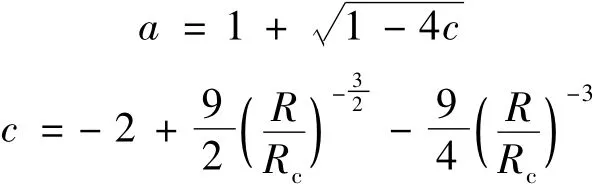
xm为湍流Taylor微尺度面积测度;Rc为 线性稳定性理论得到的临界Re数，注意到仅仅由Re数确定，这与实验的观测相符合.

根据上述理论，可以认为:湍流能量级串由一系列的旋涡非线性分岔过程刻画，呈现Feigenbaum倍周期分岔的途径.有关的分岔序列计算可以参见文献 ［24］.

从简单的对比可以看到本文提出的湍流级串旋涡动力学模型与β-模型有许多类似之处，但存在如下根本的区别:

1)β-模型中的离散来自假设的旋涡的概念，没有数学基础，而本文新模型中离散的出现有物理数学原因;

2)β-模型中尺度的演化只有递减的模态，并且是人为设定的，没有动力学基础.

6 结论

本文简要回顾了有关湍流能量级串问题的概念的源起和演化，简要评述了目前各种研究方法的局限性.最后给出了本文在这一方向上基于Karman-Howarth方程的研究进展.主要结果表明:湍流能量级串由一系列的旋涡非线性分岔过程刻画，呈现Feigenbaum倍周期分岔的途径，这定量地反映出湍流能量级串中的非线性相互作用.

References)

［1］Monin A S，Yaglom A M.Statistical fluid mechanics vol2:mechanics of turbulence［M］.Massachusetts:MIT Press，1975

［2］Frisch U.Turbulence:the legacy of A N Kolmogorv［M］.Cambridge:Cambridge University Press，1995

［3］Richardson L F.Weather predicition by numerical process［M］.Cambridge:Cambridge University Press，1922

［4］Kolmogorov A N.The local structure of turbulence in incompressible visocus fluid for very large Reynolds numbers［J］.Doklady Akademiia Nauk SSSR，1941，30:9－13

［5］Kolmogorov A N.A refinement of previous hypotheses concerning the local strucutrue of turbulence in viscous incompressible fluid at high Reynolds number［J］.J Fluid Mech，1962(13):82－85

［6］Batchelor G K，Townsend A A.The nature of turbulent motion at large wave numbers［J］.Proc R Soc Lond A 1949，199(1057):238－255

［7］Obukhov A M.Some specific features of atmospheric turbulence［J］.J Fluid Mech，1962(13):77－81

［8］Novikov A A.Intermittency and scale similarity in the strcture of a turbulent flow ［J］.Prikl Mat Mech，1971(35):266－277

［9］Mandelbrot B B.Possible refinement of the lognormal hypothesis concerning the distribution of energy dissipation in intermittent turbulence ［J］.Statistical Models and Turbulance，1972，12:333－351

［10］Novikov A A，Stewart R W.Intermittency of turbulence and the spectrum of fluctuations of energy dissipation［J］.Izv Akad Nauk SSSR Geofiz，1964，3，408 －413

［11］Mandelbrot B B.Intermittent turbulence in self-similar cascades:divergence of high moments and dimension of the carrier［J］.J Fluid Mech，1974，62:331－358

［12］Kraichnan R H.On Kolmogorov’ s inertial-range theories［J］.J Fluid Mech，1974，62:305－330

［13］Frisch U，Sulem P L，Nelkin M A simple dynamical model of intermittent fully developed turbulence ［J］.J Fluid Mech，1978，87:719－736

［14］Lorenz E N.Deterministic nonperiodic flow ［J］.J Atmos Sci，1972，20:130－148

［15］钱俭.混沌、湍流和非平衡统计力学［J］.中国科学基金，1989(2):30－33

Qian Jian.Chaos，turbulence and nonequilibrium statitistical mechanics［J］.Chinese Natrual Science Foundations，1989(2):30－33(in Chinese)

［16］Burgers J M.A mathematical model illustrating the theory of turbulence［J］.Adv Appl Mech，1948，1:171－199

［17］Desnyansky V N，Novikov E A.The evolution of turbulence spectra to the similarity regime［J］.Izv Akad Nauk SSSR Fiz Atmos，1974，10:127－136

［18］Kerr R M，Siggia E D.Cascade model of fully developed turbulence［J］.J Stat Phys，1978，19:543 －552

［19］Gloaguen C，Leorat J，Pouquet A，et al.A scalar model for MHD turbulence［J］.Physca D，1985，51:154－182

［20］Qian J.Cascade model of turbulence ［J］.Phys Fluids，1988，31:2865－2874

［21］Ran Z.New Sedov-type solution of isotropic turbulence ［J］.Chin Phys Lett，2008，25(12):4318 －4320

［22］Ran Z.One exactly soluble model in isotropic turbulence ［J］.Advances and Applications in Fluid Mechanics，2009，5(1)，41－67

［23］Ran Z.Remarks on Sedov-type solution of isotropic turbulence［EB/OL］.New York:Cornell University Library，2009［2011-06-25］.http://arxiv.org/abs/0904.2036

［24］Ran Z.Multiscales and cascading in isotropic turbulence［J］.Chinese Sci Bull，2011，56:2889 －2892