带限最佳数字基带系统误码性能分析

2012-06-21黄葆华臧国珍袁志刚

电气电子教学学报 2012年3期

黄葆华，臧国珍，袁志刚

(解放军理工大学通信工程学院，江苏南京 210007)

0 引言

数字通信系统误码率的分析是“数字通信原理”课程的一个重要教学内容。在研究噪声对数字基带系统误码性能的影响时，该课程的教材和教学中一般假设系统是无码间干扰的，且接收信号是宽度等于码元间隔的矩形脉冲，推导误码率所用数学模型如图1所示[1-5]。其中n(t)是单边功率谱密度为n0的高斯白噪声，si(t)为发送端发送的信号(设信道无衰减)。当0≤t≤T时二进制双极性时的表达式为

推导得到的最佳数字基带系统的误码率为

式中，Eb=a2Ts是发“1”码或“0”码时接收信号的比特能量。

图1 最佳数字基带接收机结构

而对于带限信道，个别教材给出了最佳数字基带系统的结构和误码率公式[6]。系统框图如图2所示，其中信道传输特性Hc(f)在信号带宽范围内为常数。H(f)=HT(f)·HR(f)为带限无码间干扰传输特性。如升余弦滚降特性，HT(f)=HR(f)=，其误码率公式则与式(2)相同。

由于教材对带限最佳系统误码性能这部分内容的讨论不是很充分，而实际信道又都是带限的，因此在实际应用中会遇到这样的问题:信道的带限性使得接收信号不再是宽度为TS的矩形信号，而是一个幅度变化的且时域无限延伸的波形，那么该如何计算误码率公式中的比特能量Eb呢?尤其在带限最佳系统的抗噪声性能仿真中，如何来设置Eb/n0这个参数呢?要回答这些实际应用中遇到的问题，须对图2所示带限最佳系统的误码性能进行推导，搞清楚与系统中其它参数间的关系。

1 带限最佳数字基带系统误码率

不失一般性，设数字信源的输出为二进制双极性随机冲激序列，幅度为A;信道中的噪声为高斯白噪声，单边功率谱密度为n0;系统传输特性为升余弦特性，即有

因此，带限最佳数字基带系统的数学模型如图3所示。

图3 最佳数字基带系统数学模型

如想求得图3所示系统的抗噪声性能，须求出用于判决的取样值(即e点信号)的概率密度函数。下面分两种情况讨论。

1)发送“1”码时

“a”点信号 sa(t)=Aδ(t)，“b”点信号 sb(t)=Aδ(t)*hT(t)，其中

由此可得

显然，“c”点波形为 sc(t)=sb(t)+n(t)，则可得“d”点波形为

其中，nr(t)为高斯随机过程，方差为

sr(t)为有用信号部分，其表达式为

滤波器输出信号波形图如图4所示。

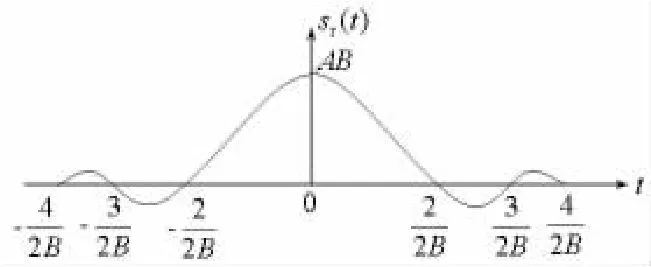
图4 接收滤波器输出信号波形

在位定时信号的控制下，当sr(t)出现最大值时对sd(t)取样，图3中“e”点的最佳取样值为

式中，nr是高斯随机过程nr(t)的取样值，方差与nr(t)相同。因此最佳取样值se是均值为AB的高斯随机变量。

2)发送“0”码时

“a”点信号 sa(t)=-Aδ(t)，按上面相同的分析过程，得到最佳取样时刻的取样值为

它是均值为-AB，方差为σn2=0.5n0B 的高斯随机变量。

由上述分析结果可得到发:“1”码和发“0”码时最佳取样值的概率密度函数，如图5所示。

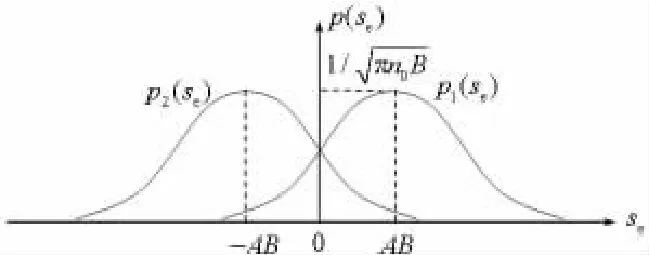
图5 发“1”，“0”时取样值的概率密度函数

当“1”和“0”等概时，可以证明最佳判决门限Vr=0，求得相应的误码率为

求接收信号sb(t)波形的能量，可以发现

将其代入式(4)，可得到与式(2)相同的误码率表达式。

由式(5)可见，Eb是发送一个比特时接收到的时域无限延伸信号的总能量。当信道无衰减时，比特能量Eb只与发送信号幅度及系统传输特性曲线下的面积有关。故当给定信号幅度和系统传输特性后，即可确定比特能量Eb。

2 基于System View的性能仿真

根据图3所示的最佳带限系统数学模型，在System View平台上构建的仿真系统如图6所示。

图6 带限信道最佳数字基带系统System View仿真

图6中的图符0、1和2构成信源，产生二进制双极性随机冲激序列。图符5、6分别为平方根升余弦特性的发送和接收滤波器，图符7、8和20仿真功率谱密度可变的加性高斯白噪声信道，图符14、10实现在最佳时刻取样，图符9完成判决，图符16～19对误码率进行统计，图符19显示误码率。

根据式(5)，设置信源参数和升余弦传输特性即可确定接收信号的比特能量Eb。本仿真系统中，我们设置升余弦传输特性的带宽为B=2000Hz，A=5×10－7V ，即 Eb=5 ×10－10J。再将图符 8 中的功率谱密度n0设置为 5×10－10W/Hz，使初始 Eb/n0=0dB。再适当设置可变增益图符20的参数以改变n0的大小，使Eb/n0从0dB开始每次递增1dB至9dB。仿真得到的误码率曲线如图7所示。将其与式(2)所示的理论误码率比较，可见仿真结果与理论值几乎重合。