户式中央空调系统的复合控制器设计

杨世勇，徐国林

（1.烟台大学计算机学院，山东烟台264005；2.烟台职业学院电气工程系，山东烟台264000）

1 引言

随着国民经济的迅速发展和人民生活水平的不断提高，空调已经走进千家万户。从控制对象的角度来看，空调系统有两个突出特性，一是多干扰性，系统在全年或全天的运行中，由于外部条件（如气温变化、太阳辐射、刮风下雨等）和内部条件（如室内照明的启停、人员数量的变化、开门开窗等）的变化，都将对运行中的空调系统造成热干扰；二是纯滞后特性，其特点是：当控制作用产生后，在一段时间内，被控参数完全没有响应而得不到及时的调整，这段时间称为“纯滞后”时间，含有纯滞后的过程必然会产生明显的超调，并需要较长的调节时间。多干扰和纯滞后特性都会对控制过程产生非常不利的影响，这些特性被公认为较难控制的过程。本文将以国内比较普及的冷／热水机组型户式中央空调为研究对象，针对上述的两个特性，提出了一种复合控制方案，在Matlab环境下进行了控制器设计和仿真研究，消除了上述不利因素的影响，获得了满意的控制效果。本文重点介绍复合控制器设计的整个过程，方案设计简单，实现容易，对于实现同种类型对象的控制具有一定的参考价值。

2 控制对象的数学模型

2.1 户式中央空调工作原理概述

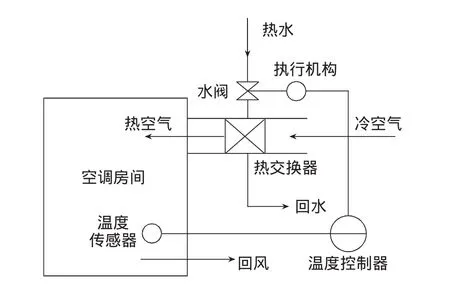
图1 系统工况示意图

图1中，由室外冷热水机组产生的热水，通过管路系统输送到空调装置中的热交换器，而室外的冷空气则被送风机送到热交换器，冷空气在热交换器中被加热后变成热空气，热空气再由送风机送到空调房间为房间供热。调节水阀就可控制进入热交换器的热水流量，进而控制室内的温度。在图1中，以空调房间和热交换器为被控对象，以空调房间的温度作为被控参数，由温度传感器、温度控制器和执行机构组成了反馈控制系统。系统控制原理如图2所示。

图2 系统控制原理框图

2.2 空调房间对象的数学模型

对于空调房间这个被控环节，其输出就是整个控制系统的输出，室内温度y，输入是热交换器的送风温度y1（参见图2）。根据能量守恒定律，单位时间内进入室内的热量减去单位时间内流出室内的热量等于空调房间内热量储存量的变化率，据此运用热力学原理建立热力学平衡方程，经过化简整理后得到空调房间的微分方程为：

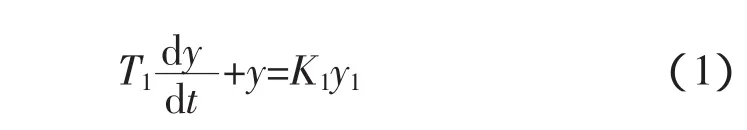
式中：T1为空调房间的时间常数；K1为空调房间的放大系数。

将上述一阶微分方程进行拉氏变换，并考虑到实际系统中存在时间延迟τ，最后得到传递函数形式的空调房间对象数学模型为：

取 K1＝6，T1＝12，τ＝5s代人得

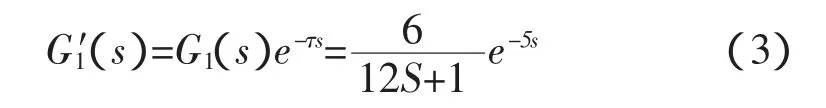
2.3 其它环节的数学模型

若忽略传感器和执行器的惯性，则：

（1）温度传感器：y2＝K2y

其中：y2是空调房间的温度检测值，K2为传感器的放大系数，取 K2＝1。

二是人口增长因素。有利面是我国人口增长速度得到了有效控制，节水理念得到了一定程度的普及，减轻了资源压力；人口空间流动改善了部分地区的资源过载状况。不利面是人口持续增长，农田灌溉系数仍较低，城市人口舒适性需求持续提升，水资源缺口依然很大。

（2）执行器：w＝K3u

其中：w是执行机构的输出，u是温度控制器的输出，K3是执行器的放大系数。

（3）热交换器的微分方程：

其中：T4为热交换器的时间常数；K4为热交换器的放大系数。拉氏变换后得热交换器的传递函数：

将执行器系数K3与式（5）相结合，得到执行器和热交换器两个环节对象的传递函数：

取 K3K＝5，T4＝7 得：

综合上述式（3）和式（7）最终得到整个控制对象的传递函数为：

3 控制器设计

3.1 PID控制器-初步设计

PID控制器传递函数的一般表达式为：

其中：kp为比例增益；ki为积分增益；kd为微分增益。设计的关键是确定这三个增益的值。这里运用工程实践中常用的Ziegler-Nichols调整法，初步设计整定出 PID 控制器 3 个参数为：kp＝0.0922；ki＝0.0059；kd＝0.3573。基于上述的 PID 控制器参数和上节的对象传递函数式（8），构建反馈控制系统如图3（a）所示，并在Matlab环境下进行仿真，假定给定的温度值为20℃，则输出响应仿真曲线如图3（b）的虚线所示，最大超调量达到了40%，控制性能很不理想。

图3 PID控制

式（9）中的微分环节kds通常称为纯微分或理想微分，其主要缺陷是微分作用时间很短，还容易引进高频干扰。在实际应用中通常在微分环节加入低通滤波器1／（1＋Tfs），可使控制性能得到改善，将式（9）的微分环节改进为kds／（1＋Tfs），其中Tf是低通滤波器的时间常数，通常取Tf＜＜kd，这里取Tf＝0.1kd。这时的PID控制叫不完全微分（或实际微分）PID控制。微分环节改进后，系统输出仿真响应曲线如图3（b）的实线所示，控制性能有所改进，但此时超调量仍然很大，这主要是由于控制对象中存在纯滞后环节，此时，单纯的PID控制难以取得满意的效果，必须采取进一步的措施。

3.2 Smith补偿-消除纯滞后影响

由上小节可知，由于纯滞后环节的存在，使被控量不能及时反映控制信号的作用，导致系统出现严重的超调，单纯的PID控制无法获得满意的效果，这里采用工程实践中通常采用的方法-Smith补偿控制方法。Smith补偿控制自被提出以来已经有多种改进的形式，但无论何种形式目的都是克服纯滞后的影响。本文所采用的补偿控制原理如图 4（a）所示。

图4 PID控制＋Smith补偿器

在图3（a）的基础上，在PID控制器后面增加一条支路，与原控制对象并联相加。虚线框内的部分就是Smith补偿器，它的传递函数Gsb（s）为：

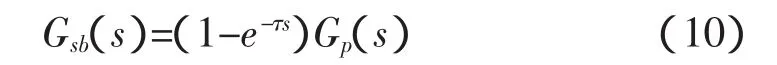
它与原控制对象并联相加后对象的传递函数为Gp（s），这样在系统的输入输出间不再表现为纯滞后特性，传递函数特征方程中消除了时间滞后项，也就消除了纯滞后对系统的不良影响，从而改善系统的性能。通过图4（b）加入Smith补偿器前后仿真曲线的对比，可充分证明补偿器的上述补偿作用。

3.3 前馈控制器-消除干扰影响

前面所研究的内容都没有考虑系统受到干扰因素的影响。当考虑干扰N（s）的作用时，系统原理如图5（a）中实线部分所示。假定干扰N（s）为可测干扰且为阶跃信号，当N（s）＝3即系统受到一个3℃阶跃干扰时，系统的输出出现了很大的超调，如图5（b）的虚线所示。

图5 PID控制＋Smith补偿器＋前馈控制

要克服干扰的影响仅靠反馈控制效果很不理想，这时，前馈控制能够很好地弥补了反馈控制这一缺点。前馈控制是针对扰动量进行控制的，其基本原理参见图5（a），图中虚线框内的Gd（s）即为所设计的前馈控制器，在图5（a）中若要使前馈控制器完全补偿干扰作用，其传递函数只要满足：Gd（s）＝-1／G2（s），则可完全消除可测扰动N（s）对系统输出的影响。将G2（s）的值代入得：Gd（s）＝-1／G2（s）＝-（7s＋1）／5＝-（1.4s＋0.2），其中 1.4s是动态分量，0.2是静态量，前者是纯微分，实际中纯微分也要加入低通滤波器1／（1＋T′fs）进行改进，原因和原理与前面设计PID控制器时相同，改进后的前馈控制器为：

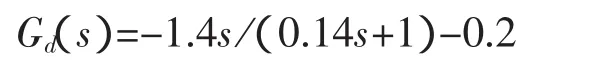
加入前馈控制后输出响应曲线见图5（b）的实线，控制性能得到极大提高。

本节全面介绍了复合控制器的设计过程，最后将各控制器的控制性能指标列在表格1中，通过这些仿真实验数据的对比，充分证明了各方案设计的正确性和有效性。

表1 各控制方案的性能对比

4 结论

具有多而强的干扰和大滞后的工业过程，在过程控制领域被公认是较难控制的对象，采用单一的控制方法往往不能取得很好的效果。本文以户式中央空调作为研究对象，针对上述两个控制难点，设计了一种复合型控制器，比较圆满地解决了问题，获得了满意的控制效果。方案设计原理简单，实现也比较容易，对于过程控制领域类似对象的控制器设计提供实用参考价值。

［1］李金川，郑智慧.空调制冷自控系统运行与管理［M］.北京：中国建材工业出版社，2002.

［2］李宜达.控制系统设计与仿真［M］.北京：清华大学出版社，2004.

［3］刘金琨.先进PID控制 MATLAB仿真［M］.北京：电子工业出版社，2005.

［4］魏克新，王云亮，陈志敏.MATLAB语言与自动控制系统设计［M］.北京：机械工业出版社，1997.

［5］王正林，郭阳宽.过程控制与Simulink应用［M］.北京：电子科工业出版社，2006.

［6］于海生，潘松峰，于培仁等.微型计算机控制技术［M］.北京：清华大学出版社，1999.