一种隐式广义预测自校正控制算法及其仿真研究

符晓玲

（昌吉学院物理系，新疆昌吉831100）

1 引言

在众多的预测控制算法中，近年来研究最活跃的，同时成果也最多的是D.W.Clarke等人于1987年提出的广义预测控制（Generalized Predictive Control，GPC）算法［1-3］。广义预测控制作为一种新型的远程预测控制方法，集多种算法的优点于一体，具有较好的性能。现有多种修正算法，大体上可分为显式算法和隐式算法两种。显示算法是先辨识对象模型参数，然后利用Diophantine方程作中间运算，最后得到控制律参数，由于要作多步预测，就必须多次求解Diophantine方程，因要经过繁琐的中间运算，故计算工作量较大，占线时间较长。隐式算法不辨识对象模型参数，而是根据输入／输出数据直接辨识求取最优控制律中的参数，因而避免了在线求解Diophantine方程所带来的大量中间运算，减少了计算工作量，节省了时间［4-6］。

为了验证隐式算法的可行性和优越性，本文将对其算法进行介绍，并进行仿真研究，分析仿真结果，总结参数变化对整个系统性能的影响。

2 单输入单输出系统的隐式广义预测自校正控制算法

2.1 并列预测器

GPC的最优化控制律

要求ΔU必须知矩阵G和开环预测向量f，原因是控制量加权因子λ和经柔化后的设定值向量W均属已知量。隐式自校正方法就是利用输入／输出数据，根据预测方程直接辨识G和f。

以前根据预测理论，为了预测超前输出，引入Diophantine方程得到的最优输出预测值为：

根据式（2）可得n个并列预测器为：

分析式（3）可知，矩阵 G 中所有元素 g0，g1，…，gn-1都在最后一个方程中出现，因此仅对式（3）的最后一个方程辨识，即可求得矩阵G。

2.2 矩阵的求取

在式（3）的最后一个方程中，令

则式（3）的最后一个方程可写为：

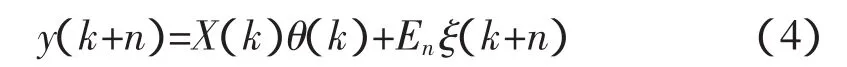
输出预测值为 y（k＋n／k）＝X（k）θ（k）或

本课中，按照学生的认知规律，教师把对食物网的探究进行梯度设计，首先请学生阅读《有趣的“猫和牛”》，学习达尔文研究食物网的方法和角度。学生发现数量变化后，也领悟到了寻找生物间的关系是蕴含在其中的方法。教师再请学生结合一日三餐，思考：人是否属于食物链（网）中的一员？我们从食物中获得了什么？能量主要储存在哪里？引导学生从数量、物质、能量三个角度进行探究。为了提升探究的有效性，教师进一步组织如下活动：

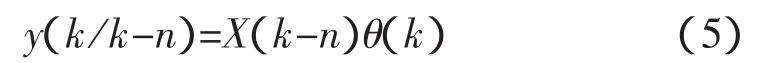
若在时刻 k，X（k-n）元素已知，Enξ（k＋n）为白噪声，就能用普通最小二乘法估计参数向量θ（k），然而通常Enξ（k＋n）不是白噪声，因此采用将控制策略与参数估计相结合的方法，即用辅助输出预测的估计值来代替输出预测值 y（k／k-n），且认为与实际值 y（k）之差为白噪声 ε（k）。

θ（k）可用以下递推最小二乘公式估计为：

式中：λ1为遗忘因子，0＜λ1＜1。

k时刻n步估计值可由下式算出，即

2.3 预测向量f的求取

根据GPC与动态矩阵控制（DMC）控制规律的等价性，GPC中的f向量相当于DMC中的Y0向量，可得到下一时刻的预测向量f为

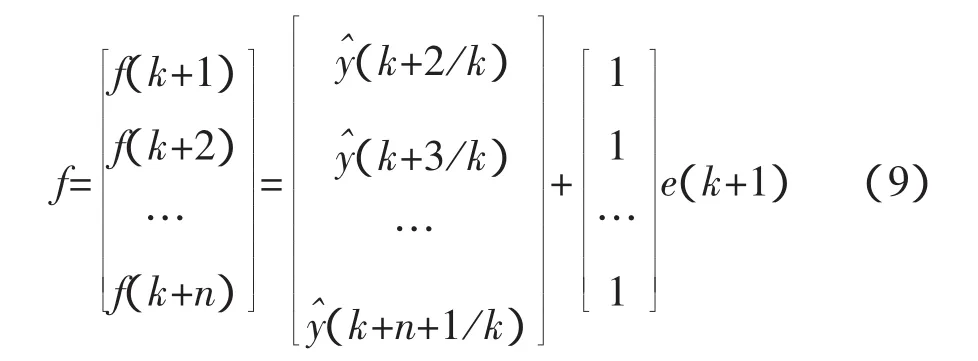
在G和f求得后，就可利用式（1）计算控制量，在计算的每一步，都能得到此步至以后n步各点上的n个控制序列。为及时利用反馈信息决定控制量，每次仅将序列中的第一个控制量作用于系统，其后的n-1个控制量不直接作用于系统，而只用于＾的计算。

2.4 控制律的简化

在自校正方案中，可从式（1）看出，每次计算必须在线求解一次 n×n 维逆阵（GTG＋λI）-1，在这里与基本的GPC一样，也引入控制时域长度，m（m≤n）当 j＞m 时，有 Δu（k＋j-i）＝0，从而矩阵 G 变成 n×m维，矩阵（GTG＋λI）则变成了 m×m 方阵，降低了维数，减少了计算工作量。对阶数较低较易控制的简单系统，可取 m＝1，这时（GTG＋λI）将由矩阵变成一个标量数值，而整个运算过程将不会有矩阵运算。

2.5 GPC控制算法中的主要参数

对GPC来说，影响其性能的主要参数主要有以下几个。

（1）采样周期T

采样周期T直接影响到g0，g1，…，gn-1和gT矩阵。采样周期T的选择，原则上应使采样频率满足香农定理的要求，即应大于2倍截止频率。T大有利于控制稳定，但不利于抑制扰动。T太长，将会丢失一些有用的高频信息，无法重构出连续时间信号，且使模型不准，控制质量下降；T也不能太短，否则机器计算不过来，且有可能出现离散非最小相位零点，影响闭环系统的稳定。

（2）预测长度n

预测长度n对系统的稳定性有重要的影响。若控制长度m很小，控制加权系数λ＝0，即在控制增量不受压制的情况下，增大n总可以得到稳定控制；若m为任意，通过加大λ，当∑gi＞0时，可得到稳定控制。

n对系统的动态特性也有影响。当n较小时，系统动态性能较差，增加n，可明显改善动态性能，增强系统的鲁棒性。但n过大，对进一步改善系统的动态性能作用不大，反而会增加计算时间，一般取 n＝5-15。

（3）控制长度m

控制长度m对系统的性能影响较大。较小的m，对控制起到一定的约束作用，使输出变化平缓，有利于控制系统稳定；而偏大的m，表示有较多步的控制增量变化，增大了系统的灵活性和快速性，但往往产生振荡和超调，引起系统的不稳定。因此，m的选择应兼顾快速性与稳定性，一般取m＝1-3。

（4）控制加权系数λ

增加λ，控制量减少，输出响应速度减慢，有益于增强系统的稳定性；但过大的λ会使控制量的变化极为缓慢，系统得不到及时的调节，反而会使动态特性变坏，一般取 0＜λ＜1。λ＝0 时，对控制量无约束。

（5）柔化系数α

柔化系数α对系统的鲁棒性有重要的影响。若α小，跟踪的快速性好，鲁棒性差；增加α，系统的快速性变差，而鲁棒性提高，故α的选择必须在动态品质与鲁棒性之间折中考虑，一般取0＜α＜1。

3 单输入单输出系统的仿真研究

为验证该控制策略的有效性，对非最小相位系统进行仿真。考虑系统模型为：

将这个非最小相位系统与非线性环节构成非线性控制系统，如图1所示。

图1 具有非线性特性的非最小相位控制系统

取参数：p＝n＝6，m＝2，λ＝0.8，α＝0.3，λ1＝1；RLS参数初值：gn-1＝1，f（k＋n）＝1，Po＝105I，其余为零；ξ（k）为［-0.2，0.2］均匀分布的白噪声，可得如图 2 所示特性曲线。

图2 跟踪给定值特性曲线（m＝2，λ＝0.8，α＝0.3）

为了比较参数变化对系统特性的影响，再取一组参数：p＝n＝6，m＝2，λ＝0.6，α＝0.3，λ1＝1；RLS 参数初值：gn-1＝1，f（k＋n）＝1，Po＝105I，其余为零；ξ（k）为［-0.2，0.2］均匀分布的白噪声，可得如图 3 所示特性曲线。

由图2和图3可以看出，按照前面的方法来选择参数，系统能够较好的工作。而λ的引入是为了抑制过于剧烈的控制增量，以防止系统发生剧烈振荡。比较图2和图3，当λ从0.6变为0.8时，控制量减少，输出响应速度减慢，但稳定性增强了。因此，增加λ，输出响应速度减慢，有益于增强系统的稳定性。

图3 跟踪给定值特性曲线（m＝2，λ＝0.6，α＝0.3）

4 结束语

本文通过对广义预测控制进行改进，介绍了隐式广义预测自校正控制算法，并进行了仿真研究。通过仿真结果验证了该算法的优越性和可行性，并分析了参数变化对整个系统性能的影响，从而为广义预测控制在工业生产中的应用提供一定的依据。

［1］钱积新，赵均，徐祖华.预测控制［M］.北京：化学工业出版社，2007.

［2］Clarke D W，Mohtadi C，Tuffs P S.Generalized Predictive Control，Part Ⅰ ：The Basic Algorithm ［J］.Automatica，1987，23（2）：137-148.

［3］Clarke D W，Mohtadi C，Tuffs P S.Generalized Predictive Control，Part Ⅱ：Extensions and Interpretations［J］.Automati-ca，1987，23（2）：149-160.

［4］刘丽丽.基于广义预测控制的中频感应加热系统温度控制［J］.科学技术与工程，2009，9（2）：415-418.

［5］陈希平，朱秋琴，王彩霞.广义预测控制算法的研究［J］.控制工程，2005（5）：35-37.

［6］王东风.基于CARMA模型的广义预测控制解耦设计［J］.自动化技术与应用，2001，20（6）：5.