基于模糊逻辑控制的SRD仿真实现

周 翔

（湖南工业大学电气与信息工程学院，湖南株洲412008）

1 引言

开关型磁阻电动机调速系统（SRD）是20世纪80年代发展起来的一种新型交流调速系统。以其结构简单、运行可靠、高性能等优良特性，成为现代交流调速系统中的一支强有力的新军，应用前景十分广阔［1］。SRD作为一种新型调速系统，兼有直流传动和普通交流传动的优点，但由于SR电机的双凸极结构和采用开关性的供电电源，使得SR电机的特性和控制方式与传统电机有明显不同，尤其是非线性以及饱和现象，造成SR电机的模型难以解析，比较突出的问题是转矩脉动和噪声［2-3］。

本文采用了智能化转矩控制系统，提出了一种新型控制策略，同时利用模糊逻辑优化主开关的导通角θon和关断角θoff，以补偿位置检测环节和其它非线性因素引起的误差，实现瞬时转矩控制。整个智能化控制系统能有效减小转矩脉动和提高系统的动、静态性能，同时具有实现简单、可靠、鲁棒性好等优点。

2 SRM控制系统

本文以DSP为核心构成的SRD系统采用双闭环调速方法，如图1所示。系统有两个反馈环，即速度外环和电流内环。速度反馈信号ωr取自位置传感器输出的转子位置信号，被给定速度ωr＊相减后作为速度环PI调节器的输入，而速度调节器的输出信号则作为电流指令值i＊再与由霍尔传感器测到的实际相电流i值比较，形成电流偏差，以控制PWM信号的脉宽，产生PWM控制信号，控制一定频率的方波脉冲宽度，宽度被调制的方波信号加到基极驱动电路，控制功率变换器主开关器件的导通与关断，将施加到SRM绕组上的直流斩波成对应频率和占空比的方波，从而实现SRD在一定调速范围内恒转矩控制。同时利用模糊方法优化导通角θon，以补偿SR电机非线性磁特性数据建模误差和转子位置传感器的精度误差，从而进一步减小电机转矩脉动。

图1 开关磁阻电动机调速系统（SRD）框图

3 建立SR电动机仿真模型

3.1 SR电动机数学模型

SR电动机由于其双凸极结构、磁路和电路的非线性、开关性等特点，定子绕组电流和磁通波形极不规则。精确分析电动机的特性必须用非线性分析的方法，具有饱和非线性磁路的SR电动机的相电感可由傅里叶级数近似逼近［4］。

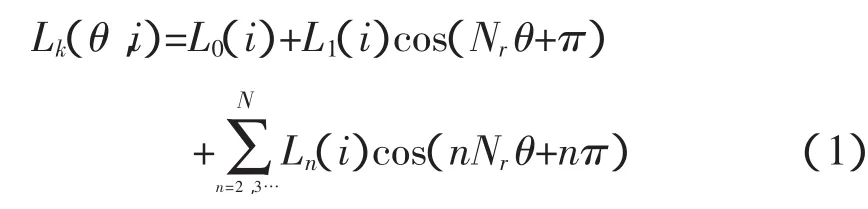
考虑到相电感的谐波分量远小于基波分量，可忽略不计，则相电感可近似表达为：

其中，L0（i）、L1（i）由式（3）确定：

Lmin、Lmax可通过实测或计算得到其随相电流变化的数据。Lmin为转子凹槽中心线与定子凸极中心线重合位置处的电感，因对应的气隙很大，铁芯不饱和，故可认为Lmin不随电流变化［5］。Lmax（i）为定转子凸极中心线重合位置处的电感，其可用多项式级数来近似表达其和相电流的函数关系，即：

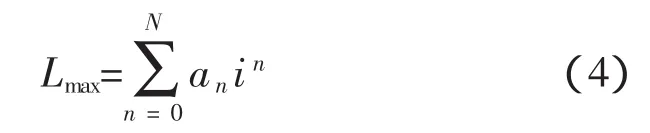
SR电动机相绕组产生的电磁转矩为：

则四相SR电动机的总电磁转矩为：

3.2 基于模糊控制器优化的SR电动机仿真模型

SRD的控制参数主要有：角速度ω、绕组电流i、开关角 θon和 θoff［6］。在此 4 个参数中，ω 为设定值，绕组电流i的大小可由θon和θoff来调节。因此θon和θoff是SRD的主要控制变量。对一定的转速和转矩，θon和θoff可以有不同的组合，因而存在对θon和θoff最优选择的问题［7］。木文采取模糊控制方法来调节 θon和 θoff。

对于本系统而言，θon和θoff的控制约束条件如下：

变量取值的条件：0＜θon＜π／6，θon＝θoff；

θon不能前移过大，因为前移越多，电流越大，当电流达到上限时，因系统的限幅斩波作用会引起转矩突降，导致系统不稳定。

本系统的模糊角度控制为二维模糊控制器，其输入为速度ω和电流i，输出为导通角变化量Δθ，模糊控制器实时对Δθ进行调整，改变的导通角θon由式（7）确定：

模糊控制器的各语言变量的论域为：速度ω＝［0 2 1 0］（rad／s），电流 I＝［0 1 0］（A），输出 Δθ＝［0 7＊π／180］（rad）。输入、输出变量的模糊子集数都取为5个，为了便于实现和保证系统可靠运行，相应的隶属度函数为三角形函数［8］。根据实际运行过程和操作的经验，总结出模糊控制规则如表1所示。

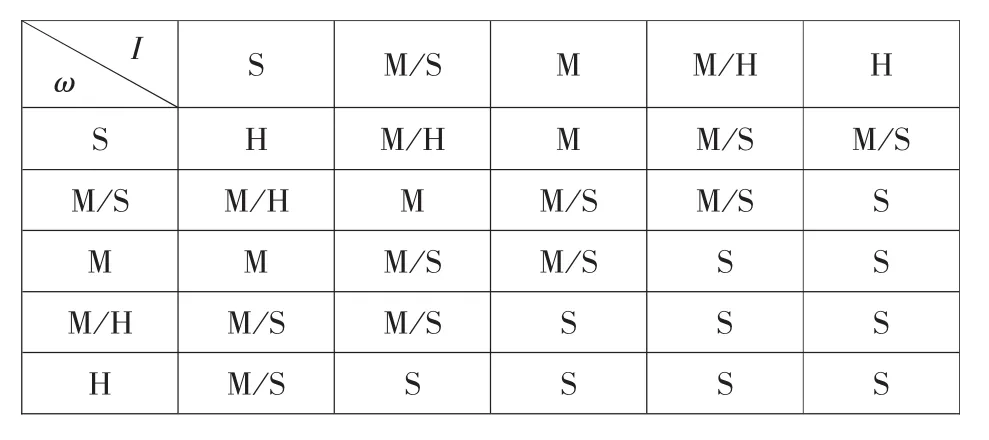
表1 关断角补偿Δθ模糊控制规则表

采用Mamdani推理法，选择模糊算子Max和Min，用重心法实现反模糊运算。经计算机在线运行得到模糊控制器输入输出关系曲面，如图2所示。

图2 模糊控制器输入输出关系曲面

4 动态仿真结果分析

通过分析上述SRM非线性数学模型及SRD系统框图，对系统进行仿真实验。系统仿真时，整个系统分解成4个模块：控制器模块、通断逻辑模块、功率变换器模块和SRM模块，其中控制器包括瞬时转矩分配、闭环磁链控制、模糊逻辑优化开关角等环节组成。

仿真时，采用一台8／6 SR电动机作为被控对象，额定转速为1500r／min，额定功率为 1500W，绕组电阻R＝0.15Ω。仿真基本参数为：直流电压Us＝260V，初始导通角为 5＊pi／180rad，初始关断角为 24＊pi／180rad，J＝0.0015，F＝0.0183，PWM 斩波周期为 0.6ms，电流采样周期为 0.5ms，仿真结果如图3、4所示。

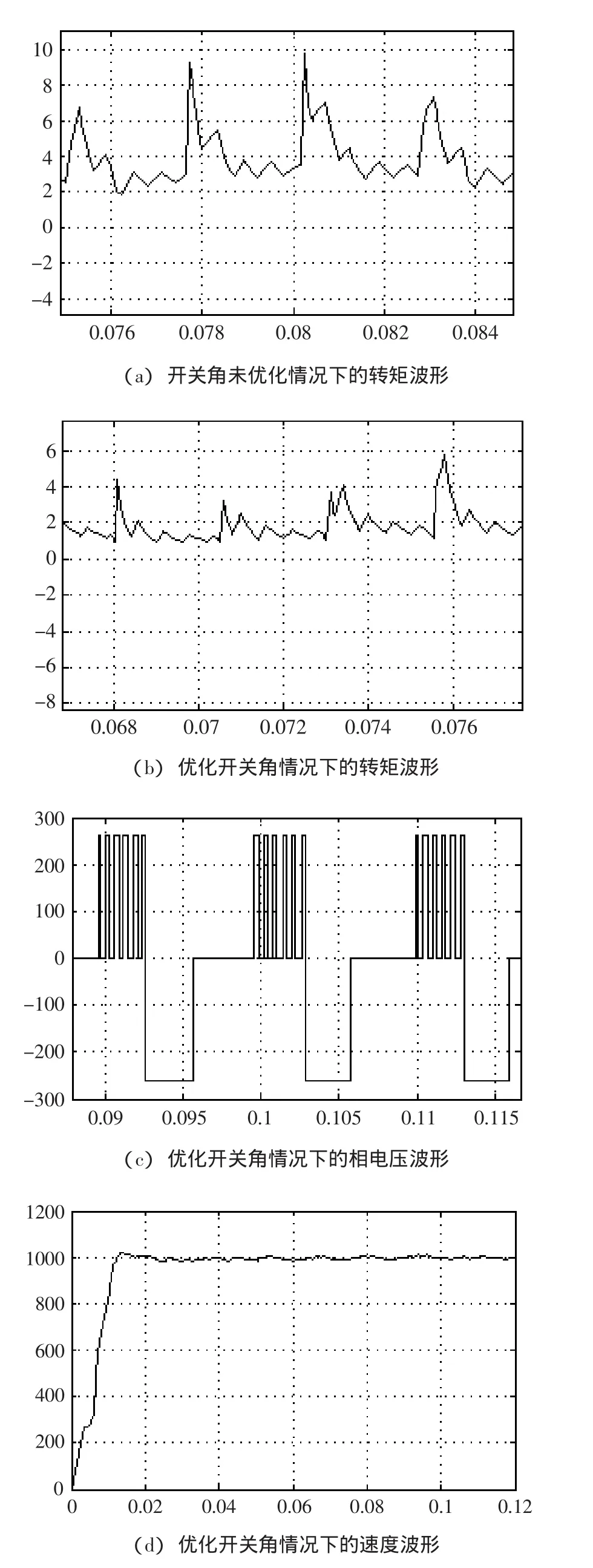
图3 给定速度 n＝1000r／min，Kp＝10，Ki＝85 时，空载情况下系统波形图

图4 给定速度 n＝1500r／min，Kp＝10，Ki＝85 时，优化开关角及空载情况下波形图

比较图3（a）和图 3（b），在相同速度下通过实时补偿关断角，SRD的转矩波动明显减小；比较图3（a）和图 4（b），在不同的速度下，SRD 能有较好的恒转矩输出；从图 3（d）和图 4（a）可以看出 SRD实际转速能迅速跟踪给定转速。

由仿真分析可知，实际转速始终能迅速跟踪给定转速、超调小、无静差，说明系统反应快速。基于模糊逻辑来优化SRD的导通角θon和关断角θoff能有效地抑制转矩脉动，采用的模糊控制器通过优化θon和θoff可以补偿其它非线性因素的影响。仿真结果表明，整个控制系统在保证其它动、静态性能的基础上，极大地降低了转矩脉动。

5 结论

本文在对整个SRD系统的工作原理及SRM内部电磁关系分析的基础上，在避免繁琐计算的前提下，又考虑到磁路的饱和效应，提出了SRM的一种非线性电感模型，且对其做了简化处理。同时利用模糊逻辑优化主开关的导通角θon和关断角θoff，以补偿位置检测环节和其它非线性因素引起的误差，并在此基础上建立了基于模糊逻辑控制的四相（8／6极）SRM的非线性电感特性的SRD动态仿真模型。系统仿真实验验证了该SRD仿真模型的正确性、合理性、有效性，仿真结果表明该控制方式能有效减小转矩脉动和提高系统的动、静态性能，同时具有实现简单、可靠、鲁棒性好等优点，且在实际SRD中易于实现，为研究SR电动机不同速度调节方式奠定了一定的理论基础。

［1］顾明磊，王双红，孙剑波.开关磁阻电机发电控制系统仿真研究［J］.微电机，2009，（1）：82-85.

［2］周素莹，林 辉.减小开关磁阻电机转矩脉动的控制策略综述［J］.电气传动，2008，（3）：11-17.

［3］许爱德，樊印海，李自强.空间电压矢量下SRM转矩脉动最小化［J］.电机与控制学报，2010，（1）：35-40.

［4］Rahman，K M，Schulz，S E.Design of high-efficiency and high-torque-density switched reluctance motor for vehicle propulsion［J］.IEEE Transactions on Industry Applications，2002，138：1500-1507.

［5］F Soares，P J Costa Branco.Simulation of a 6／4 switched reluctance motor based on Matlab／Simulink environment［J］.IEEE Trans，2002，37（3）：989-1000.

［6］Choi C，Kim S，Kim Y，et al.A new torque control method of a switched reluctance motor using a torque-sharing function［J］.IEEE Trans on Magnetics，2002，38（5）：3288-3290.

［7］Natan Tzvi Shaked，Raul Rabinovici.New procedures for minimizing the torque ripple in switched reluctance motors by optimizing the phase-current profile［J］.IEEE Transactions on magnetics，2005，41（3）：1184-1192.

［8］N Bhiwapurkar，N Mohan.Torque ripple optimization in swit ched reluctance motor using two-phase model and optimization search technique［C］.SPEEDAM 2006 International Symposium on Power Electronics，Electrical Drives，Automation and Motion.s42，2006：12-17.