一类非线性随机系统的自适应预测控制

侯晓秋，陈志学

（1.黑龙江科技学院电气与信息工程学院，黑龙江哈尔滨150027；2.中国兵器工业第205研究所，陕西西安710065）

1 引言

自 1982 年 Billings等提出 NARMAX 模型［1］以来，针对于NARMAX模型的辨识和控制问题的研究已形成Billings学派，因人工神经网络可逼近任意非线性系统，已提出许多控制算法，采用多模型逼近NARMAX模型的多模型自适应控制算法，我国学者韩志刚，侯忠生提出的无模型控制，各种采用时变线性模型逼近NARMAX模型的控制算法，采用动态切平面逼近NARMAX模型的控制算法等。文献［2］给出的基于一步时滞情形的NARMAX模型的最小预测误差自适应预测控制器的准则函数具有局限性，致使算法存在稳态偏差，文献［3］对文献［2］的准则函数进行改进，所提出的控制算法无稳偏，文献［4］研究了NARMAX模型的多重时滞情形，文献［2-4］的算法只适用于确定性情形，本文研究多重时滞随机性NARMAX模型的自适应预测控制问题。

2 一类非线性随机系统的NARMAX模型

Billings等提出NARMAX模型：

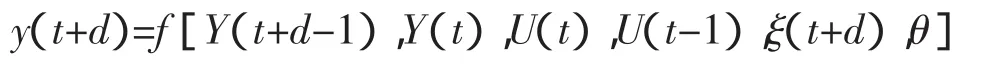
其中：y（t）为系统输出，y（t）∈R1；U（t）为系统的m 维输入，U（t）∈Rm；ξ（t）为系统干扰量，ξ（t）∈R1；Y（t＋d-1）为系统 t＋1 时刻至 t＋d-1 时刻输出的集合；Y（t）为系统到t时刻为止的输出的集合，U（t-1）为系统到t-1时刻为止的输入的集合；ξ（t＋d）为系统止t＋d时刻的干扰量的集合；θ为未知参数；d为系统时滞，f（…）表示一般的非线性函数。因ξ（t）一般是无法测量的，故其在f（…）中出现的形式难以确定，所以上式NARMAX模型实用性差，这里将NARMAX模型的各种随机干扰等效在系统的输出端，当等效的干扰为平稳随机序列时，基于文献［5］线性滤波和谱分解定理及成型滤波器原理构成一非线性随机系统模型：

其中：η（t）为平稳随机序列，且

其中：e（t）为零均值，方差为 σ2的白噪声序列，而

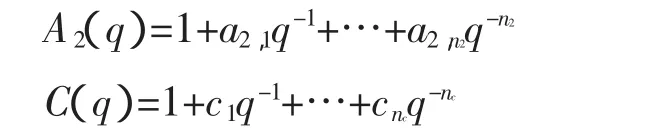
这里假设n2，nc已知，A2（q-1）和C（q-1）为稳定多项式。

3 四个假设条件

假设1：系统（1）式输入输出可观测的，可控制的，即对某一系统有界的期望输出信号，存在有界的可行控制输入信号，使得系统在此控制输入信号的驱动下，其输出等于系统的期望输出。

假设2：f（…）关于Y（t＋d-1）及U（t）的偏导数是连续的，且各偏导数有界。

假设3：由泰勒展开公式，在工作点Y0（t＋d-1），U0（t）处用线性的动态切平面去逼近一般的非线性系统式（1）时，假设有：

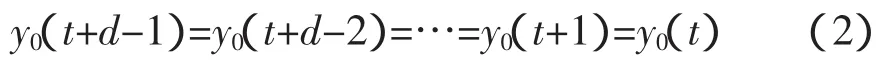
其中：

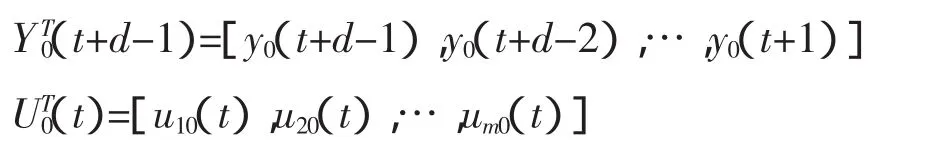
这里，假设3中的y0（t），U0（t）一般可为：

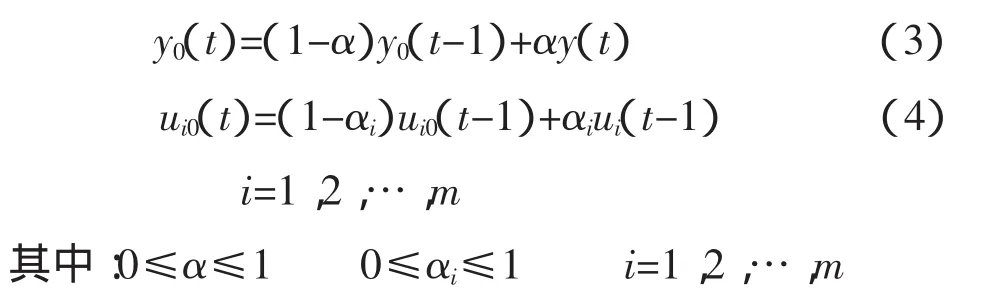
假设 4：d、n2、nc，已知。

假设1-3对多数非线性系统成立的分析见文献［4］。

4 动态切平面逼近非线性系统

在工作点Y0（t＋d-1），U0（t）处对式（1）的非线性系统用动态切平面逼近，由一阶泰勒展开公式得：

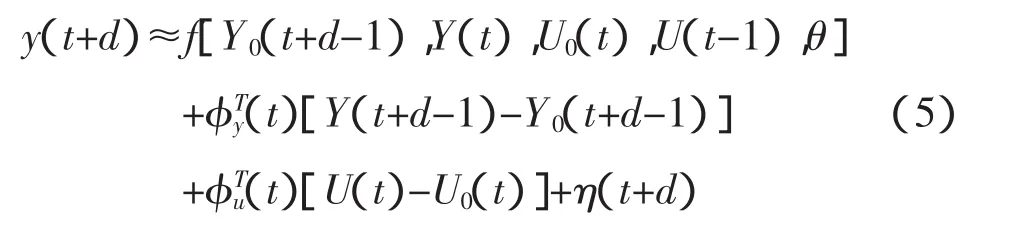
其中：

而

整理写成，

其中：

而

这里，D（t）在t时刻是一个已知的量。

将式（2）代入式（8）整理得：

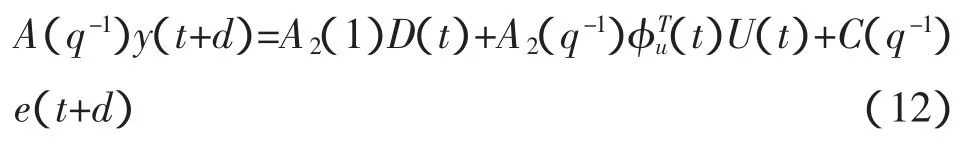
其中：

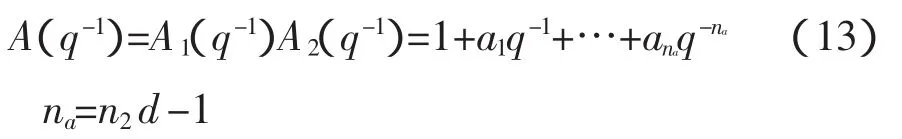
5 广义最优预测

对于式（12），定义辅助输出 s（t＋d）为，

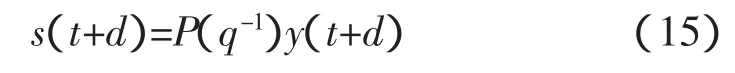
其中：

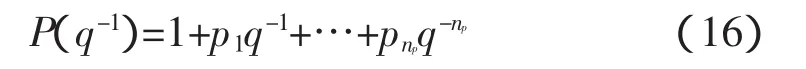
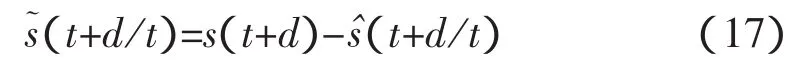
可用如下引理阐述广义最优预测：

引理1：广义最优预测，满足预测误差方差，

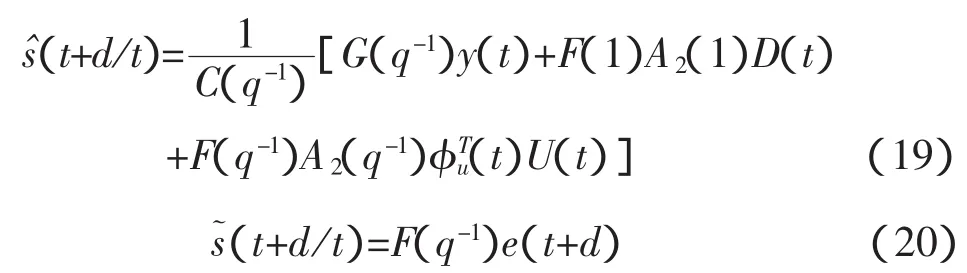
其中：G（q-1）、F（q-1）满足以下阿斯特罗姆恒等式，

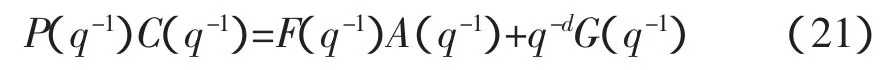
式中：

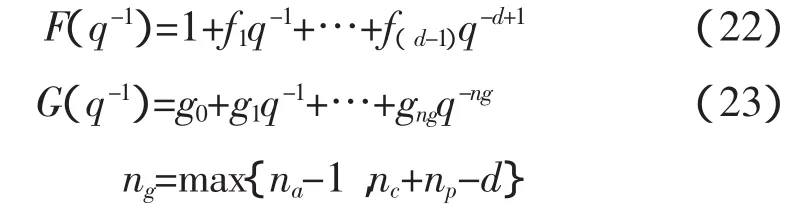
证明：参考文献［6］可证。

6 自适应预测控制算法

6.1 预测控制算法

控制输入准则函数为，

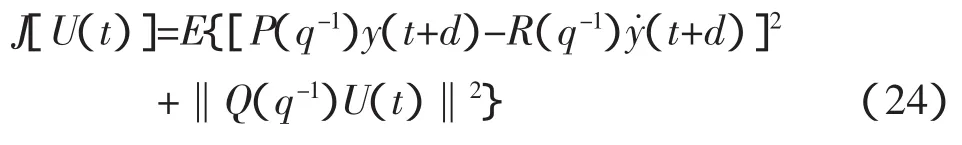
而

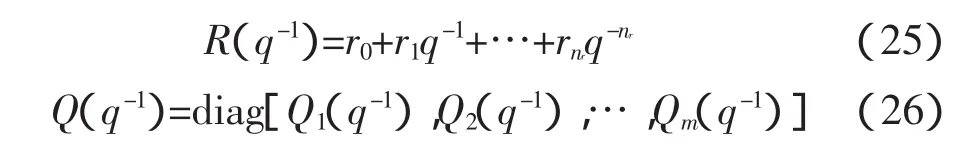
且

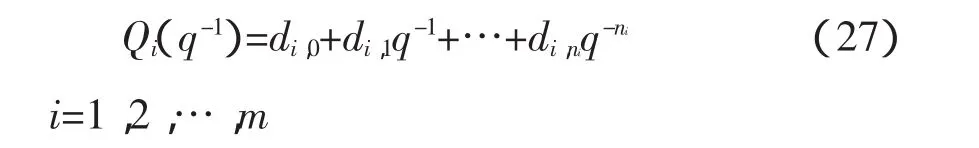
定理1：对于非线性随机系统式（1），满足假设条件1-4，基于式（24）控制输入准则函数的预测控制器算法为：

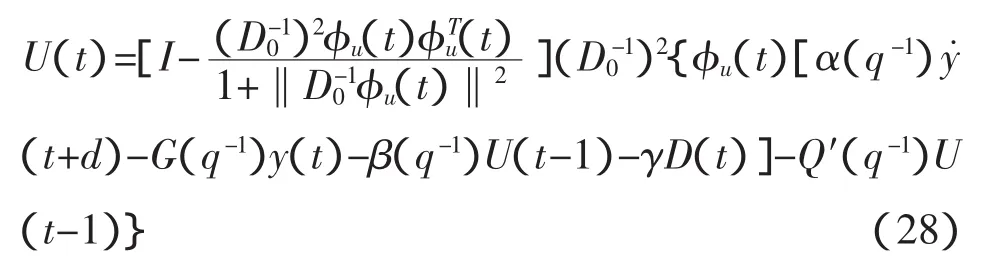
其中

证明：参考文献［2、3、4、6］证明如下：

上式等价于如下准则函数：

由 J＊［U（t）］对 U（t）求偏导，

由式（19）得：

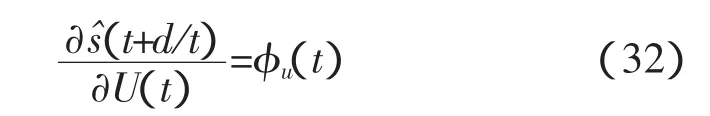
整理得：

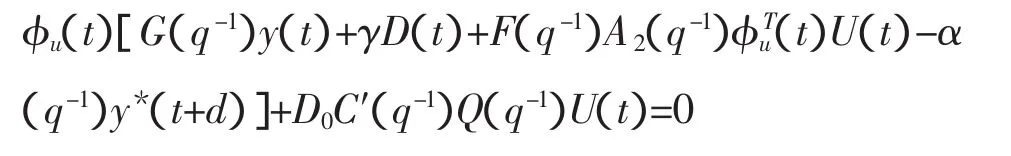
得：

可得：

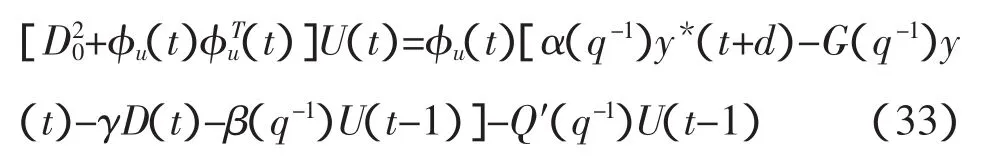
［7］的矩阵反演公式得：

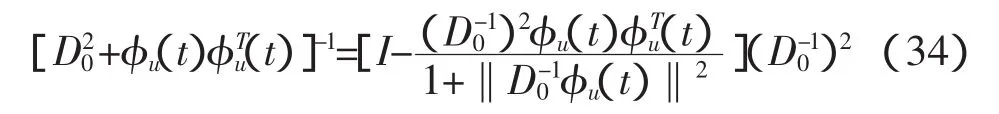
式（34）代入式（33）即得式（28）算法。

6.2 自适应预测控制算法

当式（1）模型参数未知时，可采用文献［8］的非线性参数估计算法估计其值，结合引理1的广义最优预测算法和定理1的预测控制算法，构成自适应预测控制。

7 仿真研究

已知系统的形式为：

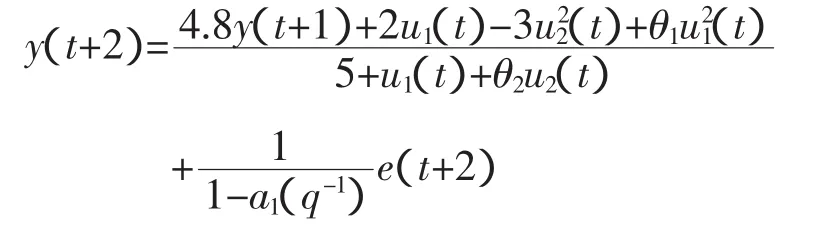
其中：θ1，θ2，a1的真值为：

U0（t），y0（t）选取如下：

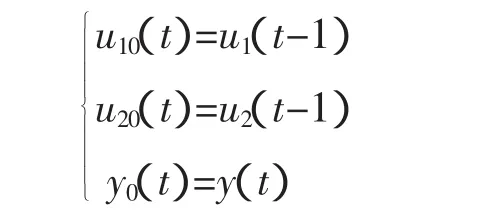
参考输入为：

结合现阶段工程造价工作的信息化发展，虽然已经得到了绝大部分企业的认同，也积极进行了多方面的尝试，但是在具体落实中却同样也存在着多方面的缺陷和不足，具体问题表现如下。

u1（t）及u2（t）的限幅为：

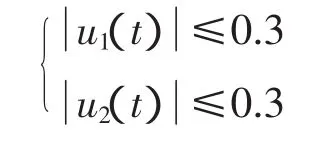
白噪声，

参考文献［3，4］的鲁棒控制策略，使系统无稳偏，且控制输入收敛于以原点为中心的变化域内，

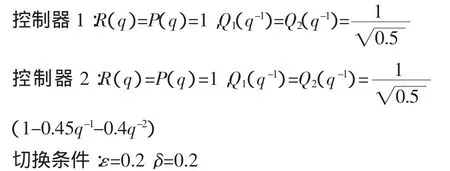
采用文［8］的参数估计算法，仿真结果如图1、图2、图3所示。由图1可知系统的输出响应曲线在0≤t≤100时不理想，这是由于算法开始时系统未知参数偏离其真值过大造成的，但系统能稳定运行，说明算法的鲁棒性好。

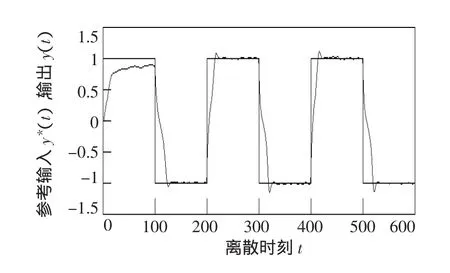
图1 输出响应曲线

图2 控制信号u1（t）的变化曲线

图3 控制信号u2（t）的变化曲线

8 结束语

文中研究了一类非线性随机系统的控制问题，所提出的模型较Billings等提出NARMAX模型具有实用性，控制算法适用于时变随机系统，且系统无稳态偏差，控制输入收敛于以原点为中心的变化域内，具有应用参考价值，进一步可研究其自适应广义预测控制算法和多变量情形。

参考文献：

［1］Billings，S.A.，and Leontaritis，I.J.Parmeter estimation techniques for nonlineat systems ［J］，6th IFAC Symp.Ident，and Syst.Par.Est.，1982：427-433.

［2］侯忠生.非参数模型及其自适应控制［M］.北京：科学出版社，1999，98-101.

［3］侯晓秋.非线性确定性系统的鲁棒自适应控制器［J］.黑龙江科技学院学报，2003，13（2）：54-57.

［4］侯晓秋.多重时滞非线性系统的自适应预测控制［J］.黑龙江科技学院学报，2008，18（2）：137-139.

［5］韩曾晋.自适应控制［M］.北京：清华大学出版社，1995.70-76.

［6］Clarke D W ，Gawthrop P J.Self-tuning controller［J］.Proc.IEE，1975，122（9）：929-934.

［7］方崇智，萧德云.过程辨识［M］.北京：清华大学出版社，1994.146-147.

［8］侯晓秋.非线性随机系统的具有遗忘因子的递推最小二乘法［J］.黑龙江科技学院学报，2008，18（4）：306-309.