基于矩阵旋转的改进STBC码

滕志军，张 伟，王 娜

(东北电力大学信息工程学院，吉林吉林132012)

将编码技术和阵列技术有机结合在一起是空时编码(Space-Time Coding)的最大特点。STBC(Space-Time Block Coding)是空时编码的一种，在不需要增加额外频率资源的情况下具有良好的分集性能［1］，对于克服信道衰落非常有效［2］，因此能增加传输可靠性。Alamouti提出了一种简单的正交空时编码的设计［3］，这种编码方案是一种简单、全速率的空时编码方案。采用2根发射天线、多根接收天线，能实现全码率、满分集的效果。但是当天线数目大于2的时候，这种编码所使用的复正交阵是不存在的。为了进一步的提高数据的传输速率，准正交编码［4］方案开始出现，如ABBA码和Jafarkhani码。这类编码在实现全码率发送的同时降低了分集增益。改进准正交编码的方案有星座变换、矩阵旋转、预编码等方法。文献［5］利用发送端的信道信息，使用线性预编码处理准正交空时码，达到了提高系统的性能的目的;文献［6］采用了MPSK与QPSK相结合的混合星座编码方式，在发射端利用信道状态信息对信号进行预处理，以便在接收端正确恢复信号，降低误码率或提高系统吞吐率。

本文提出了一种基于矩阵旋转的正交空时分组码来解决非正交空时分组码信道相关矩阵中存在自干扰项的问题。该方案通过对非正交空时分组码信道相关矩阵采用矩阵旋转(Givens)的方法来构造正交的空时分组码。由于Givens旋转可将向量的任意元素置为零，因此可以有效消除自干扰项。此外，该码还可降低误码率，在接收端采用线性解码。

1 空时分组编码

空时编码(STC)技术基于空间分集技术，采用多发射和多接收天线，将发射分集和接收分集技术相结合，是MIMO-OFDM系统的研究热点之一。主要思想是利用空间和时间的编码实现空间分集和时间分集。可以补偿信道衰减，增加系统的容量，抑制噪声和干扰，降低误码率，并获得很高的编码增益和分集增益。空时分组编码(STBC)如图1所示。

图1 空时分组编码器

1.1 Alamouti发送分集方案

Alamouti于1998年提出了两个发射天线的空时分组码，之后空时分组码以其简单的性能和结构引起广泛关注，进入到3GPP标准。Alamouti发送分集方案如图2所示。

编码和发送序列在一个给定的时间符号内，两个信号同时从两个天线发出，从天线1发出的为信号x1，从天线2发出的信号为x2。在第二个符号时间内，信号x*

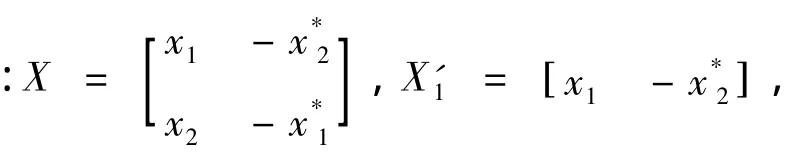
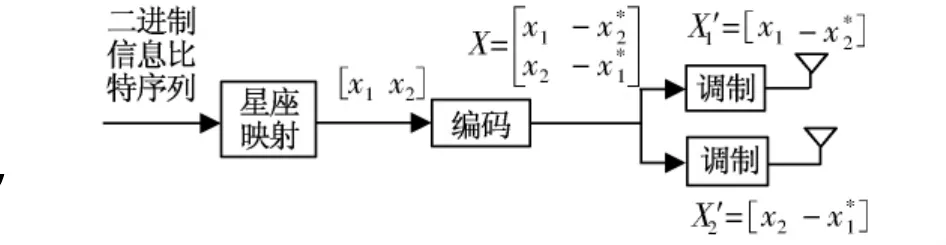
图2 Alamouti发送分集方案

所以它具有正交特性(式中，上角标*表示变量的复共轭，上角标H表示矩阵的希尔伯特变换)。这种正交特性会使译码变得相对简单，并且根据衡量分集好处的秩准则(rand criterion)，这种正交矩阵可以获得满增益。同时，它在2个符号周期内发送了2个码元符号，根据Rate=k/p不难看出码率为1，即为全码率。

1.2 基于Alamouti方案的准正交码

对于实正交设计的空时分组码来说，只有当发射的天线数为2、4、8时，编码速率为全速率，即Rate=1，而对于复正交设计的空时分组码来说只有当天线数为2时存在正交矩阵，Tirkkonen等和Jafarkhani分别提出了2种不同的准正交空时分组编码(TBH码和Jafarkhani码)。它们都是针对四发一收类的通信系统，并且这种编码的子模块都是Almouti码。准正交码的好处是能实现编码码率为1，但由于它们不满足正交特性，所以不能达到满分集增益，系统可靠性就会受到影响。

其中，TBH即(ABBA)编码方案的矩阵模型为:

因为

式中I4为4×4的单位阵。

由式(3)可知，TBH编码并不是正交的，同时它的最小秩是2。对于这种四发一收的通信系统，它的分集增益是2。同理，可以得到Jafarkhani码也具有相似的情况。

2 基于矩阵旋转的正交空时分组码

对TBH编码，考虑具有一个接收天线时的情况，信道向量h=［h1h2h3h4］T，其中hi(i=1，…，4)表示从发射天线i到接收天线的复信道增益。假设信道为准静态平坦Rayleigh衰落信道，在4个连续的码符周期内，接收信号向量R0=［r1r2r3r4］T可表示为:

n=［n1n2n3n4］T表示复高斯白噪声向量。对接收信号R0=［r1r2r3r4］T的第二项和第四项分别取共扼，得到式(5)的等价关系

令检测矩阵

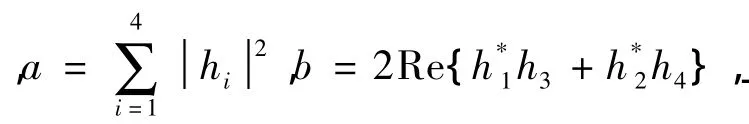
从式(7)可以看出，由于TBH码的非正交性在检测矩阵中引入了自干扰项，使得线性解码变得难以实现。由矩阵变换的理论，选取合适的旋转矩阵R1、R2，应用Givens旋转G(i，j，θ)可以将检测矩阵A'4的非对角线元素xij(i≠j)变为零，得到预处理检测矩阵

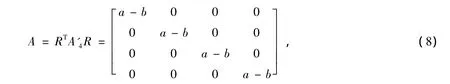
式中R=R1R2。

将预处理的检测矩A写成预处理的信道矩阵的共轭转置乘预处理的信道矩阵的形式:

令预处理信道矩阵Hm=HR，由式(9)可知Hm为正交矩阵，其表达式为:

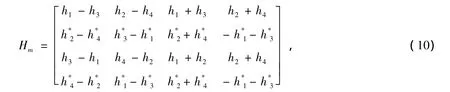
由于

求出Hm对应的编码矩阵如下:

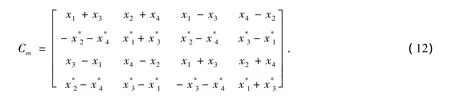
可见编码矩阵Cm是准正交的，但是可以使其对应的信道矩阵正交化，因此在接收端可以采用最大似然译码从而降低译码的复杂度。并且文献［7］已证明，最大似然译码具有最小错误概率，性能优异。

3 改进的基于旋转矩阵的正交空时分组码

为进一步改善其性能，把TBH码中的第二个Alamouti复子矩阵码旋转一定的角度θ，令C=Ejθ，旋转角度后的TBH码如下:

接收信号

对接收信号的第二项和第四项分别取共轭，得到式(14)的等价式

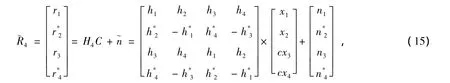
H4是有效信道矩阵，C是信号向量。与正交空时分组码类似，计算检测矩阵

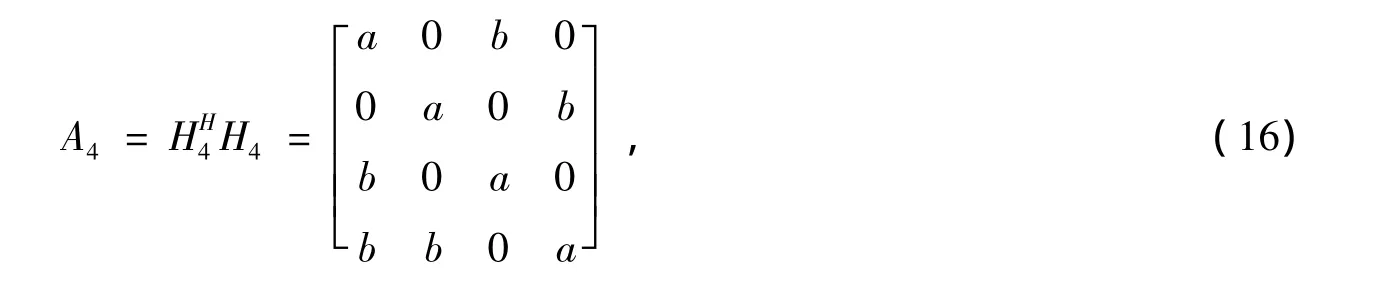
用R1、R2对检测矩阵A4进行两次Givens旋转，即预处理检测矩阵，

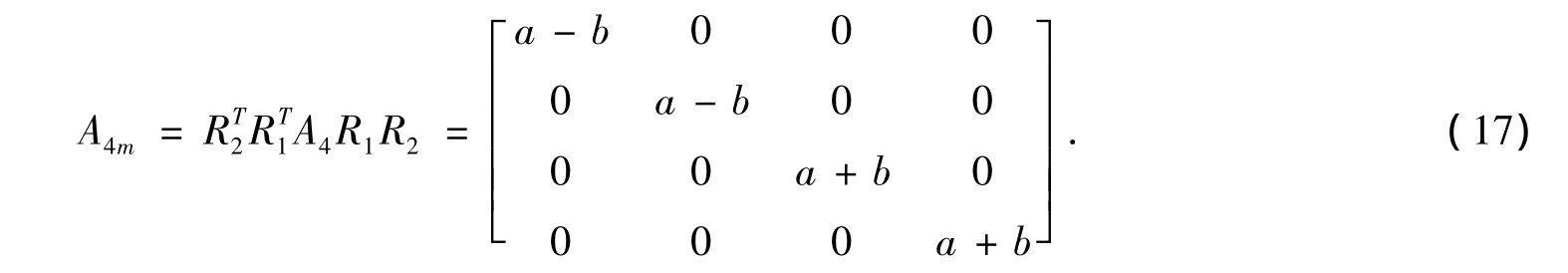
令R=R1·R2对预处理检测矩阵进行如下变换

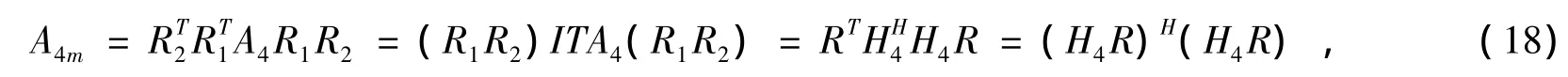
令预处理信道矩阵H4m=H4·R由(18)可知H4m为正交阵，表达式为

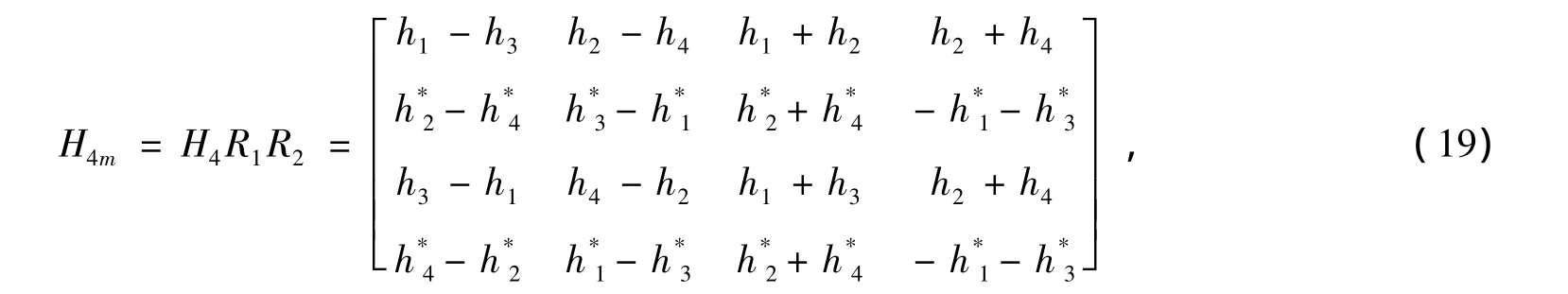
与预处理的信道矩阵H4m相对应的编码矩阵Cm如下:

在接收端直接采用最大似然译码可实现独立译码

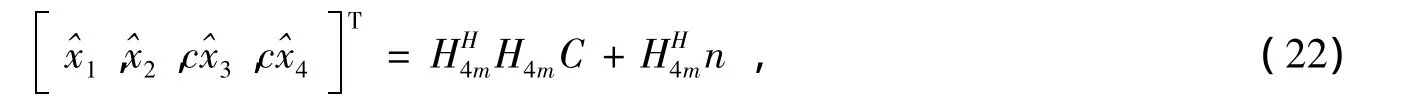
4 仿真结果和分析

为了便于研究，在仿真过程中假定无线信道为准静态瑞利衰落信道，信道矩阵中各元素均为统计独立零均值，单位方差复高斯随机变量。并且接收端已知准确的信道衰落信息。信道保持周期为一个编码块(4个符号间隔周期)，且不同的信道之间是完全独立的。

本文所采用的仿真平台为MATLAB7.0系统，具有易操作性和开放性［8］。信源采用QPSK调制方式，空时编码采取Alamouti编码结构和准正交空时分组码，三种空时编码仿真结果表明，本文采用的基于矩阵旋转技术的空时分组码具有较好的抗干扰性能，误码率低。

图3给出了两发一收通信系统中准正交空时分组码，Alamouti码和改进的空时分组码在准静态信道下的误码性能比较曲线。图3中横坐标为信噪比(SNR)，是接收天线端有用信号总平均功率和噪声平均功率的比值，纵坐标为误码率。根据仿真结果可以看出，在低信噪比时，改进的方案与原有方案误码性能相差不大;在高信噪比时改进方案的误码性能较原有方案好。

图3 抗干扰性对比

5 结 论

通过仿真结果可以看到:文中改进后的旋转正交空时分组码与准正交码相比，和在系统性能方面有了明显的改善。基于这种角度反馈的空时编码可以进一步应用到多发多收系统，并且可以和OFDM技术有很好的结合，这些优点将会使改进方案有着很好的理论价值和应用前景。

［1］羿宗琪，王钢，李鸿林.空时编码的OFDM系统研究［J］.哈尔滨理工大学学报，2006，11(5):69-71.

［2］王慕坤，徐春霖，杨明极.采用分集技术改善遥测系统性能［J］.哈尔滨理工大学学报，2000，5(5):12-19.

［3］ALAMOUTI S M。A simple transmit diversity technique for wireless commun-ications［J］.IEEE Journal on Select Areas in Communications，1998，16(8):1451 -1458.

［4］SHARMAN，PAPADIASCB.Improved quasi-orthogonal codes through constellation rotation［J］.IEEE Trans Wireless Commun，2004，51(3):332-335.

［5］郑秀萍，刘丽，张水利.基于ZF预编码的STBC-MIMO-OFDM系统性能的研究［J］.机械管理开发，2010，25(4):203-204.

［6］尹训锋，刘敬芝，曾凡鑫.合星座编码的全速率全分集准正交空时分组码［J］.电子信息对抗技术，2007，22(5):33-42.

［7］张锐，张礼勇.多载波系统多用户信号检测的一种新算法［J］.哈尔滨理工大学学报，2005，10(4):57-61.

［8］董秀洁，王莉，王素菊.一种改进的LS信道估计算法［J］.哈尔滨理工大学学报，2009，14(1):47-49.