等几何分析方法求解静电场非齐次边值问题

2012-06-12胡志强徐喜荣

电波科学学报 2012年5期

张勇林皋胡志强徐喜荣

(1.大连理工大学建设工程学部，辽宁大连 116024； 2.大连理工大学电子信息与电气工程学部，辽宁大连 116024)

引言

计算电磁学是电磁学分析的一种重要工具，其中对静电场求解是最为基础和重要的环节。计算电磁学的求解方法主要有解析法、半解析法和数值解法三大类。解析法和半解析法虽然能够得到精确或半精确的解析式，但只适用于简单的求解域、简单的物理参数的问题，不具有通用性。数值解法虽然是在一定条件下的近似解法，但具有较强的通用性，最为常见的有有限差分法、有限元法、边界元法、矩量法、无网格法[1-8]等。其中，有限元法是应用最为广泛的数值方法。各类数值方法都需要对求解域进行二次离散或者建模，而离散之后的计算模型可能与原模型不具有一致性，从而丧失精度。

等几何分析方法(IGA)是2005年由Hughes[10]率先提出的一种新型数值方法。该方法避免了传统数值方法中求解模型与设计模型的非一致性，从而实现了将问题的分析计算构架于精确模型上，提高了计算精度与效率。目前这种方法已被用于求解固体力学和流体力学问题[11-16]。最近，张勇和林皋等将该方法应用于静电场问题[17]，利用加权余量法推导了静电场齐次边值问题的等几何分析方程，并实现了对自然边界条件和齐次强制边界条件的施加。另外，也将其应用于波导本征问题[18-19]的求解, 但在波导本征问题中，无论是横向磁场(TM)波还是横向电场(TE)波，边界条件都是齐次的。虽然等几何分析方法具有良好的计算特性和较高的计算效率，但是由于非均匀有理B样条(NURBS)基函数不具有插值性[20]，使得其求解带有非齐次强制边界条件的边值问题变得复杂和困难。

自然边界条件和强制边界条件的施加方式是不同的，自然边界条件最终转化为关于边界积分，从而对齐次或者非齐次边界并不敏感。但对于强制边界条件，需要给定离散自由度值，这对于具有插值特性的数值方法而言，是极为容易的，比如在有限元方法中，只需通过结点坐标便可计算出边界结点自由度值。但对于不具有插值特性的数值方法而言，这样是无法做到的，比如在无网格方法，张淮清等[8]给出了基于拉格朗日乘子方法施加强制边界条件，文献[9]则给出了拉格朗日乘子、罚函数法、混合法等施加边界条件，其中拉格朗日乘子最为简洁。本文在文献[17]基础上将等几何分析方法进一步拓展到静电场非齐次边值问题。建立带有拉格朗日乘子的泛函，同时对拉格朗日乘子采用等几何离散，最终得到关于控制点电势及与非齐次边界相关的控制点拉格朗日乘子的增广代数方程。考虑到拉格朗日乘子仅赋存于非齐次强制边界上，其增加的计算自由度相对于整体自由度而言较小，从而并不会影响等几何分析方法的计算效率。

应用基于拉格朗日乘子的等几何分析方法求解静电场非齐次边值问题，以顶部带有正弦分布电势的方形板以及内外壁均为非齐次边值的圆环域为数值算例。计算结果表明本文方法能很好处理静电场非齐次边值问题，通过与传统方法和解析解的比较，显示出其低自由度消耗、高效和高精度的特点。

1 基于拉格朗日乘子的静电场等几何分析方法推导

1.1 静电场非齐次边值问题

静电场问题是电磁学分析中的一个典型边值问题(BVP)，描述静电场(域内无电荷)特性的控制方程(φ为电势)为

1.2 曲面的NURBS描述

NURBS是计算机辅助设计(CAD)中几何形体的标准数学描述，是由NURBS基函数Ri,p,(i=0,1,…,n)，控制点Pi,(i=0,1,…,n)和节点向量Ξ={ξ0,ξ1…,ξm}三要素来定义的，其中，p为基函数次数，n为控制点数，m为节点数。NURBS基函数是通过B-样条有理化得到的，如一维NURBS基函数可表示为

(3)

式中:ωi是对应于Ni,p(ξ)的权值；Ni,p(ξ)为B-样条基函数，可由Cox-de Boor公式[20]递归定义为式(4)：

(4)

NURBS基函数将节点向量所在的参数空间中的点映射到控制点所在的物理空间，即NURBS参数空间的一个参数区间[ξi,ξi+1)与物理空间中的一个单元Vi相对应。

NURBS具有与B样条一样的性质，如非负性、单位分解性、紧支性、灵活连续性、线性无关性和非插值性等。但与B样条相比，它可以更准确地描述圆锥曲线和曲面。当权值相等时NURBS基函数则退化为B样条基函数。

高维NURBS基函数可由低维NURBS基函数张量积得到，如式(5)所示的二维NURBS基函数形式，p、q分别为两个方向基函数的次数。

(5)

一般地，NURBS曲面的向量形式可写为

(6)

式中，Pi,j是NURBS曲面控制点。图1给出了典型的NURBS曲面，图1(a)为空间NURBS曲面，图1(b)为平面内NURBS曲面，后者适用于二维静电场问题。

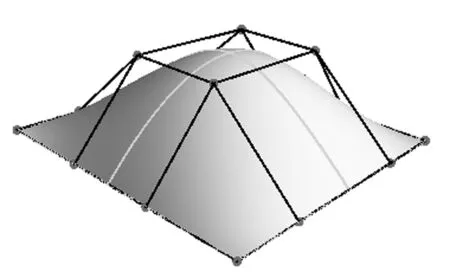
(a) 二次NURBS曲面

(b) 二次NURBS平面内曲面图1 NURBS曲面(控制点标记为·)

1.3 求解域的等几何离散与细分

在等几何分析方法中，求解域的离散模型不是二次建模得到的，而是继承于求解域的设计模型，即 CAD系统中的NURBS描述，如上节所述，对于二维问题，两个张量积方向的节点向量可表示为Ξ={ξ0,ξ1，…,ξku-1},Η={η0,η1，…,ηkv-1}.参数域内的节点区间[ξh,ξh+1)×[ηk,ηk+1)映射成求解域上的一个单元Vh,k。求解域NURBS单元Vh,k的任一点坐标表示为

=NBh,k(ξ,η)xh,k

(7)

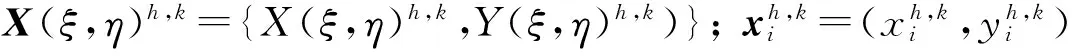
从CAD系统导入的初始模型一般并不能满足解的精度需求，需要对求解域进行细分。而在等几何分析方法中，求解域的细分是非通信的、保形的，即细分的过程无需再与原来的设计模型进行通信，并且细分前后的模型是几何一致的，这是等几何分析的重要特征，也是其与传统有限元方法的重要区别。保形细分算法有h-细化方法，p-细化方法，k-细化方法等[10]。

1.4 电势场的等参化

等参方法用于近似求解域的电势场，求解域中任一点的电势采用和式(7)相似的表示形式为：

(8)

式中，φi表示求解域控制点的电势场变量。

1.5 等几何分析方法离散方程

采用虚功原理[21]将控制微分方程式(1)及非齐次边界条件式(2)表达成带有拉格朗日乘子的泛函

(9)

对泛函Π(φ)取一次变分得

(10)

式(10)可进一步离散化为

(11)

对引入的拉格朗日乘子采用NURBS等几何离散，即

=NB(ξ,η)λ

(12)

将式(8)和(12)代入式(11)，注意到δφ和δλ的任意性，得到等几何分析方法离散方程的形式为

(13)

(14)

(15)

(16)

2 静电场非齐次边值问题的算例分析

2.1 方形槽

通过分离变量法，可得该问题的电势及电场强度解析解如式(17)所示：

(17)

数值计算时，上述问题简化为平面问题，如图2所示，其中红色点为等几何分析方法的初始网格控制点。

图2 方形槽非齐次边值问题及IGA初始网格示意图

等几何分析方法的初始网格只有一个等几何单元，不能满足计算的精度要求，利用h-细化方法，可以得到较细的网格，即网格A(含有36个控制点自由度和6个拉格朗日乘子自由度)和网格B(含有100个控制点自由度和10个拉格朗日乘子自由度)。表1为本文方法与文献[8]列出的有限差分法(FDM)、径向基无网格法(RBF)计算电势最大值误差、相对均方根误差对比。本文方法中场值计算点为65×65个，在方形槽内均匀分布。相对均方根误差ERMS和最大误差Emax计算公式为：

(18)

Emax=max(abs(φi_exact-φi_calc))

(19)

式中：φi_exact为解析解；φi_calc为数值解。

表1数据表明：网格A的结果和有限差分法的精度相当，网格 B的结果和无网格法接近，这表明本文采用拉格朗日乘子处理等几何分析方法中的非齐次边值问题是有效的。对于电场强度，由于文献[8]中没有给出计算结果和误差，故直接给出本文方法计算的电场强度相对均方根误差和最大误差，见表2.与电势数值解的精度相比，电场强度数值解的精度稍低，这是源于电场强度是电势的梯度场相关，也就是它的数值精度要比电势低。但网格A到网格B的误差减小的程度表明，本文方法的数值解有较快收敛速度。表1和表2中的Emax和ERMS就是最大误差和相对均方根误差，计算式分别为式(18)和(19)。

表1 电势计算值的最大值误差和均方根误差列表

表2 电场强度计算值的最大值误差和均方根误差列表

上述比较初步确定了本文方法的有效性，为了进一步比较其收敛性和收敛速度，采用五种尺寸的单元划分，对于每一种尺寸的网格，分别对应一个等几何单元模型和一个传统的有限元单元模型。计算自由度数量和单元数量在表3中列出，其中，对于等几何分析方法，其计算自由度数为N+M，N为控制点自由度数，M为非齐次边界附件自由度数，即拉格朗日乘子离散自由度数。在图3中用双对数坐标表示自由度数和单元数的关系，从图3可以看出等几何分析方法的单位单元的自由度消耗要比有限元少，并且随着网格的加密，这种差距在增大。对于非齐次边值问题，需要附加自由度，但其所占的比重并不大。

表3 各种网格下的单元数量和自由度数量

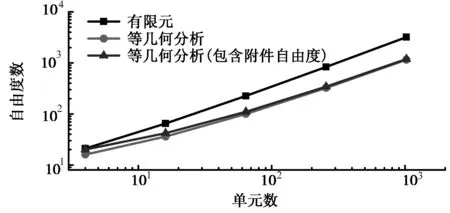
图3 计算自由度与单元数量图

(a) 电势相对均方根误差

(b) x方向电场强度相对均方根误差

对每个网格得出65×65个计算点上电势和电场强度值，并根据公式(18)和(19)计算其与解析解(17)的相对均方根误差。图4给出了这些误差随网格细化的收敛，图4(a)、(b)、(c)分别代表电势、x方向和y方向电场强度的相对均方根误差收敛图。从整体上看，电势场的误差收敛较快(在网格5中为10-7数量级)，电场强度收敛较慢(在网格5中为10-4数量级)；从电势或者电场强度收敛斜率看，等几何分析方法的收敛斜率均比有限元大，也就是说等几何分析方法的收敛速度快。

最后给出整个域上的等几何分析方法在网格5中的电势数值解分布图，如图5(看1063页)所示，(a)与(b)分别是数值解及其和解析解的相对误差分布图，图5(b)中的相对误差在10-6数量级，表明其数值解精度高。另外从误差在域内的分布可以看出，非齐次边界上解的精度要比域内解低，这表明对于非齐次边值，其上拉格朗日乘子的离散数目不能过少。

从这个简单的静电场非齐次边值问题可以看出，等几何分析方法的优势是固有的等几何性，即计算模型与设计模型一致，以及细化非通信和保形特点。但是由于其基函数的非插值性，对于非齐次边界需要额外的附加自由度，所幸的是边界自由度数是O(N)，而域内控制点的自由度数是O(N2)，其中N为一个方向上自由度的度量，即附加自由度占计算自由度的比重较小，特别是对于细网格划分情况。此外，虽然增加了计算自由度，但和传统方法相比，等几何分析方法在计算效率上具有单位单元的计算自由度消耗小、计算精度高、收敛速度快的特点。

2.2 同心圆柱环面

电位和电场强度的解析解可由极坐标下的分离变量法求得

k(Crk+Dr-k)sin(kθ)eθ

(20)

式中系数A、B、C、D可根据边界条件计算得出。在计算中，取Ra=0.5 m，Rb=1.0 m，φa1=1.75 V，φa2=0.5 V，φb1=-0.5 V，φb2=-0.5 V，k=2.

图6 圆柱环面非齐次边值问题及初始网格图

等几何分析的初始模型如图6所示，红色点表示等几何模型的控制点，其不在域内体现了控制点的非插值性。对于圆柱环面非齐次边值问题，其内壁和外壁均为非齐次边界条件，比算例1的齐次和非齐次混合边值条件要简单，但本算例模型的边界是更为复杂的曲线形式。采用六种尺寸的单元划分，对于每一种尺寸的网格，分别对应一个等几何单元模型和一个传统的有限元单元模型，各种网格下的单元数量和自由度数量如表4所列，对于网格6，有限元模型的自由度数已经超过10 000，而等几何分析方法只有不到5 000.

表4 各种网格下的单元数量和自由度数量

对每个网格计算出260(环向)×65(径向)个计算点上电势和电场强度值，并根据式(18)和(19)计算其与解析解(20)的相对均方根误差。在图7(a)、(b)、(c)中分别显示了电势和电场强度的相对均方根误差随计算自由度的收敛性，从中可以看出在网格较粗(网格1)的情况下，由于非齐次边界上附加自由度占的比重较大，使得等几何分析方法比有限元要消耗更多的自由度数，但从图中误差-自由度的斜率可以看出，随着网格加密，等几何分析方法的收敛较快。需指出是图7为双对数坐标轴，虽然两条线的距离不是很大，但体现的差别为倍数关系。

图8(看1064页)显示了等几何分析方法在网格6中的电势数值解分布，(a)与(b)分别是数值解及其和解析解的相对误差分布图，图8(b)中的相对误差在10-5数量级，与算例1相比，其精度有所下降，这说明求解域的形状及非齐次边界的数量对结果的精度有一定的影响。

(a) 电势相对均方根误差

(b) x方向电场强度相对均方根误差

3 结论

本文将等几何分析方法扩展到静电场非齐次边值问题，在虚功方程中引入拉格朗日乘子，推导出静电场非齐次边值问题的等几何分析方法求解式。修正后的等几何分析方法虽然增加了计算自由度(非齐次边界上的离散拉格朗日乘子)，但与有限元方法相比，该方法仍然具有计算自由度少、收敛速度快、计算精度和计算效率高的特点，并且非通讯保形细化方法使得模型的细分可以自动进行，更为简洁与方便。应用此方法求解了方形槽与同心圆环的静电场非齐次边值问题，结果表明该方法能够有效的求解非齐次边值问题，且具有上述的优点，可进一步在计算电磁学中推广应用。

[1] 周勤,茅乃丰.旋转对称静电场的一种新的数值解法[J].电波科学学报,1990,5(4):26-34.

ZHOU Qin,MAO Naifeng.The electrostatic field problems with representations of spline functions and their quasi-charge density analysis method[J].Chinese Journal of Radio Science,1990,5(4):26-34.(in Chinese)

[2] SONG B,FU J.Modified indirect boundary element technique and its application to electromagnetic potential problems[J].IEE proceeding-H of Microwaves Antennas and Propagation,1992,139(3):292-296.

[3] 金建铭.电磁场有限元方法[M].西安电子科技大学出版社,1998:51-70.

[4] BAMJI S S,BULINSKI A T.Electric field calculations with the boundary element method [J].IEEE Transactions on Electrical Insulation,1993,28(3):420-424.

[5] 甄蜀春,曹蕾,张继龙.波动方程差分解法对波导螺钉调配器的分析[J].电波科学学报,2005,20(1):125-127.

ZHEN Shuchun,CAO Lei,ZHANG Jilong.Analysis of screw tuner based on wave equation finite difference method[J].Chinese Journal of Radio Science,2005,20(1):125-127.( in Chinese)

[6] 汪朝晖,廖振方,陈德淑.有限元法分析尖板电极结构的空间静电场分布[J].重庆大学学报,2010,33(5):41-47.

WANG Zhaohui,LIAO Zhenfang,CHEN Deshu.Analysis of spatial electric field with point-plate electrodes configuration using finite element method[J].Journal of Chongqing University,2010,33(5):41-47.(in Chinese)

[7] 梁志伟,赵国伟,徐杰,等.柱形等离子体天线辐射特性的矩量法分析[J].电波科学学报,2008,23(4):749-753.

LIANG Zhiwei,ZHAO Guowei,XU Jie,et al.Analysis of plasma-column antenna using moment method[J].Chinese Journal of Radio Science,2008,23(4):749-753.(in Chinese)

[8] 张淮清.电磁场计算中的径向基函数无网格法研究[D].重庆：重庆大学,2008.

ZHANG Huaiqing.Research on Radial Basis Function Meshless Method in Numercial Computation of Electromagentic Field[D].Chongqing： Chongqing University,2008.(in Chinese)

[9] FERNANDEZ-MENDEZ S,HUERTA A.Imposing essential boundary conditions in mesh-free methods[J].Comput Methods Appl Mech Engrg,2004,193(12/14):1257-1275.

[10] HUGHES T J R,COTTRELL J A and BAZILEVS Y.Isogeometric analysis CAD,finite elements,NURBS,exact geometry and mesh refinement[J].Comput Methods Appl Mech Engrg,2005,194(39/41):4135/4195.

[11] REALI A.An isogeometric analysis approach for the study of structural vibrations[J].Journal of Earthquake Engineering,2006,10(Special Issue 1):1-30.

[12] BAZILEVS Y,CALO V M,ZHANG Y,et al.Isogeometric fluid-structure interaction analysis with applications to arterial blood flow[J].Computational Mechanics,2006,38(4/5):310-322.

[13] COTTRELL J A,REALI A,BAZILEVS Y,et al.Isogeometric analysis of structural vibrations[J].Computer Methods in Applied Mechanics and Engineering,2006,195(41/43):5257-5296.

[14] COTTRELL J A,HUGHES T J R,REALI A.Studies of refinement and continuity in isogeometric structural analysis[J].Computer Methods in Applied Mechanics and Engineering,2007,196(41/44):4160-4183.

[15] ZHANG Y,BAZILEVS Y,GOSWAMI S,et al.Patient-specific vascular NURBS modeling for isogeometric analysis of blood flow[J].Computer Methods in Applied Mechanics and Engineering,2007,196(31/32):2943-2959.

[16] ZHANG Y,LIN G,HU Z Q.Isogeometric analysis based on scaled boundary finite element method[J].IOP Conference Series:Materials Science and Engineering,2010,10(1):012237.

[17] 张勇,林皋,刘俊,等.等几何分析方法及其应用于偏心柱面静电场问题[J].电波科学学报,2012,27(1):177-183.

ZHANG Yong,LIN Gao,LIU Jun,et al.The isogeometric analysis and its application to eccentrically parallel cylinders electrostatic problem[J].Chinese Journal of Radio Science,2012,27(1):177-183.(in Chinese)

[18] 张勇,林皋,刘俊,等.波导本征问题的等几何分析方法[J].应用力学学报,2012,29(2):113-119.

ZHANG Yong,LIN Gao,LIU Jun,et al.The isogeometric analysis for eigen problem of waveguide[J].Chinese Journal of Applied Mechanics,2012,29(2):113-119.(in Chinese)

[19] 张勇,林皋,胡志强,等.基于等几何分析方法求解任意截面波导本征问题[J].计算物理,2012,29(4):9-17.

ZHANG Yong,LIN Gao,HU Zhiqiang,et al.Eigenvalue Analysis of Waveguide with Arbitrary Cross-section by Isogeometric Analysis[J].Chinese Journal of Computational Physics,2012,29(4):9-17.(in Chinese)

[20] PIEGL L,TILLER W.The NURBS Book [M].Berlin:Springer Verlag,1997.

[21] HUGHES T J R.The Finite Element Method,Linear Static and Dynamic Finite Element Analysis[M].New York:Dover,2000.