基于三次相位建模的天波雷达污染校正

游 伟 何子述 陈绪元 胡进峰 何 茜

(1.电子科技大学电子工程学院，四川 成都 611731；2.南京电子技术研究所，江苏 南京 210039)

引 言

天波超视距 (OTH) 雷达是一种具有超远距离目标探测和信息获取的雷达系统。天波OTH雷达不受地球曲率的影响，能实现数千公里的距离覆盖，其对低空飞行器、海面舰船目标、隐身飞机、远距离连续监测的能力，是其他雷达不可取代的[1]。国内外学者对天波超视距雷达展开了广泛的研究，并取得很多实用的研究成果[1-8]。天波OTH雷达通常工作于高频段(3～30 MHz)，与其他体制雷达不同，天波雷达信号传播需要经过电离层的反射。由于电离层本身是一种运动的传输媒质，天波雷达的回波信号不可避免的受到电离层的影响，并将造成雷达回波信号频谱的展宽。

海面的回波通常很强，这对海面的目标检测构成威胁。尤其是对于慢速目标的检测，由于其多普勒频率靠近杂波谱，很容易被杂波掩盖。由于天波雷达信号需要经过电离层的反射传播，电离层自身的上下运动将对回波信号的频谱产生频移[7]。当雷达相干积累时间(CPI)较长或电离层上下运动加剧时，频移将使得回波信号频谱展宽，这称为电离层污染。虽然有专门的频率管理系统(FMS)支持[8-9]，使得雷达能够自适应地选择合适的工作频率，在一定程度上缓解污染的问题，然而污染仍然不能完全避免。因此，研究天波污染的校正算法非常必要。

天波污染通常建模为一个乘性噪声而不是加性噪声。一般将天波超视距雷达的海杂波经过电离层传播造成的污染建模为调频信号的形式。因此，一般的天波污染校正的核心是要获得杂波原始数据中的瞬时Bragg频率分量的变化规律。获得频率变化规律后就可以通过与理论值的比较，对杂波原始数据做校正。在该领域已经提出许多算法，都取得了较好的效果。

BOURDLILLON[10]等提出使用最大熵谱法 (MESA)来对污染进行校正。这种算法将一个CPI内的杂波数据分成若干段，并且认为，在每个小段内的Bragg频率是稳定的。在每个小段内使用高分辨谱估计算法分析得到其频率。最后通过内插对CPI内的回波进行校正。这种算法在天波污染不大的情况下可以取得较好的效果，而当污染比较大的时候其效果则变差。

PARENT[11]等提出相位梯度法。这种算法很直观，即直接对相位梯度进行能量平均。但是为了提高精度，需要多个发射波形进行平均，这对于传统的雷达难以实现，将会增加雷达的复杂性。

HOWLAND[12]等提出使用Wigner-Ville分布 (WVD)算法获得信号频率并进行校正。该算法存在的问题是边界上的点估计效果较差。

MARTIN[13]等提出使用Hankel降秩(HRR)算法来对杂波进行抑制。LU[14]等对此提出了改进。即先利用HRR方法求得杂波信号的瞬时频率，利用所得到的瞬时频率对污染后的杂波作校正。再对校正后的数据进行奇异值分解，以达到对杂波的抑制。这种级联的处理使得杂波抑制效果有所提高。但是，使用HRR算法对杂波瞬时频率的估计效果受到瞬时频率的波动速度以及波动幅度的影响。当频率波动不大并且速度较缓时，HRR算法能够得到比较好的估计。而当变化稍大的时候其效果显著下降，使得其补偿效果变差。

PELEG等[15]提出使用离散多项式相位变换 (DPT)算法来获得多项式信号的各阶系数。刘颜回[16]、李雪[17]等将DPT算法应用于污染校正，并提出改进算法，都取得了很好的效果。但是这些改进措施增大了算法运算量，使得算法不能实时实现。

对被污染的回波，考虑其相位连续，可对信号分段。根据Weierstrass逼近定理，任意有限区间内的连续函数可由一个多项式无限逼近[18]。当分段较短，可以用一个三阶多项式来逼近。因此，提出使用三次相位(CP)信号对天波雷达回波信号进行建模，并在此基础上提出一种新的频率估计算法对天波污染进行校正。该算法运行较快，能够实时处理。同时，给出了算法的详细处理流程和仿真结果，仿真结果表明：在天波污染比较严重，即频率变化较大时，所提算法比HRR算法频率估计更准确。因此，具有更好的污染校正效果，可以作为天波雷达污染校正的一种方案。

1 天波雷达回波信号模型

天波超视距雷达回波信号可以写为如下形式

r(t)=c(t)+i(t)+s(t)+in(t)+n(t)

(1)

式中：c(t)为杂波(包括海杂波和地杂波)；i(t)为瞬态干扰；s(t)为感兴趣的动目标回波；in(t)为各种非平稳干扰回波；n(t)为接收机内部热噪声。瞬态干扰以及非平稳干扰都将对动目标的检测形成威胁，二者的抑制分别通过时域和空域的处理来实现，限于篇幅不做讨论。

主要研究杂波的污染。已经证明，当海面被高频信号照射时，回波信号将在固定的频率处有很强的峰值，称为Bragg峰。峰值的位置与雷达的工作频率的关系为[6]

(2)

式中：g为重力加速度；fc为雷达工作频率，Hz；c为光速，m/s.

根据Bragg模型，杂波分量的模型可以写为

c(t)=ca(t)ej2πfbt+cr(t)e-j2πfbt

(3)

式中：ca(t)=Aa(t)ejφ(t)；cr(t)=Ar(t)ejφ(t)，Aa(t)和Ar(t)为信号幅度，φ(t)为考虑到电离层扰动引起的随机相位。

电离层扰动引起的随机相位，从频域上看，是导致雷达回波信号的瞬时频率随机波动，从而造成频谱展宽。对于舰船等低速目标而言，其频谱通常很靠近Bragg谱，因此，杂波谱的展宽将使得舰船等目标的检测变得非常困难。在进行舰船目标检测时，需要对电离层的污染相位进行校正，而相位污染的校正可以等价的转化为对信号瞬时频率的估计。

2 三次相位信号的频率估计

P.O’Shea[19]提出了三次相位信号的建模方法，并将其用于对天波雷达的回波信号进行建模，在此基础上本文提出一种新的三次相位信号系数估计算法。三次相位信号可以写为

s(t)=Aej(a0+a1t+a2t2+a3t3)

(4)

式中A为信号幅度。而信号的相位可以写为

φ(t)=a0+a1t+a2t2+a3t3

(5)

式中，a0、a1、a2、a3为三次相位信号的系数，均为常数。

对信号相位求取延时有

φ(t+τ0)-φ(t-τ0)= 2a1τ0+4a2tτ0+

(6)

φ(t+τ0)+φ(t-τ0)= 2a0+2a1t+2a2t2+

(7)

定义算子

φ1(s,τ0)=s(t-τ0)s(t+τ0)s*(t)s*(t)

(8)

将相位关系代入，可以得到

(9)

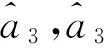
(10)

得到了系数a3的估计值后，可以将该系数用于信号的补偿，将三阶相位项消除掉，则信号仅剩下二阶相位项。对于一个二阶相位信号，定义算子φ2(s,τ0)，有

φ2(s,τ0)=s*(t-τ0)s(t+τ0)

(11)

将信号的二阶相位关系代入，有

φ2(s,τ0)=A2ej(2a1τ0+4a2τ0t)

(12)

DPT算法是对φ2(s,τ0)的FFT进行谱峰搜索，获得系数a2.观察式(12)可知，传统的DPT算法采用一个延时来估计系数a2，这里将延时τ0作为变量，即τ0连续变化，而t固定，则对于式(12)给出的信号，瞬时频率f可以写为

2πf=2a1+4a2t

(13)

写成离散形式，即2πf=2a1+4a2nT

(14)

式中T为采样间隔。从式(14)可以看出，式(12)中信号的频率与两个系数呈线性关系，如果得到信号在两个不同采样点n1和n2的瞬时频率f1和f2，则系数的估计值为

(15)

式中：

(16)

前面给出的是模拟信号下两个算子的表达式，对于离散信号，设采样下标为n，延迟系数为n0，则两个算子可以表示为

φ1(s,τ0)=s(n-n0)s(n+n0)s*(n)s*(n)

φ2(s,τ0)=s*(n-n0)s(n+n0)

为了保证两式中的下标n-n0和n+n0有意义，必须满足1≤n+n0,n+n0≤N.

至此为止，就获得了三次相位信号的各个系数的估计值，即可对该信号的频率作估计，其瞬时频率可以写为

(17)

(18)

从式(18)可以看出，如果存在估计误差，则补偿后的信号也会引入相应的相位剩余。忽略三阶项，按照前述算法，以延时τ0为变量，所得信号瞬时频率f可以写为

2πf=2a1+4a2t+6aΔ3t2

(19)

写成离散的形式，则一阶与二阶系数可以估计为

(20)

从式(20)看出，当三阶系数存在误差时，该误差传递给一阶和二阶系数，误差的大小与三阶系数估计的误差近似成正比关系。

3 天波污染校正算法

天波污染校正的关键是要捕获Bragg谱峰瞬时频率的变化，即要获得某一个Bragg谱线的瞬时频率。获得瞬时频率后，将电离层引起的污染相位补偿掉即可实现校正。一般的污染校正算法都基于这一思想。

一个被污染的Bragg信号分量可以表示为

(21)

式中m(t)为所需要求解的瞬时频率扰动。在获得瞬时频率后即可减去理论的Bragg频率而获得该扰动值，并可通过式(22)作校正，得到校正后的信号成分xc(t)：

(22)

这里利用第2节的三次相位信号来对Bragg分量进行建模，并将其用于电离层污染的校正。由于实际的Bragg分量并不是理想的三次相位，因此，这里采用分段的思想，将回波数据分成若干段，对每段内用三次相位进行建模，并获得其瞬时频率。基于三次相位建模的校正算法流程如图1所示，可以描述为：

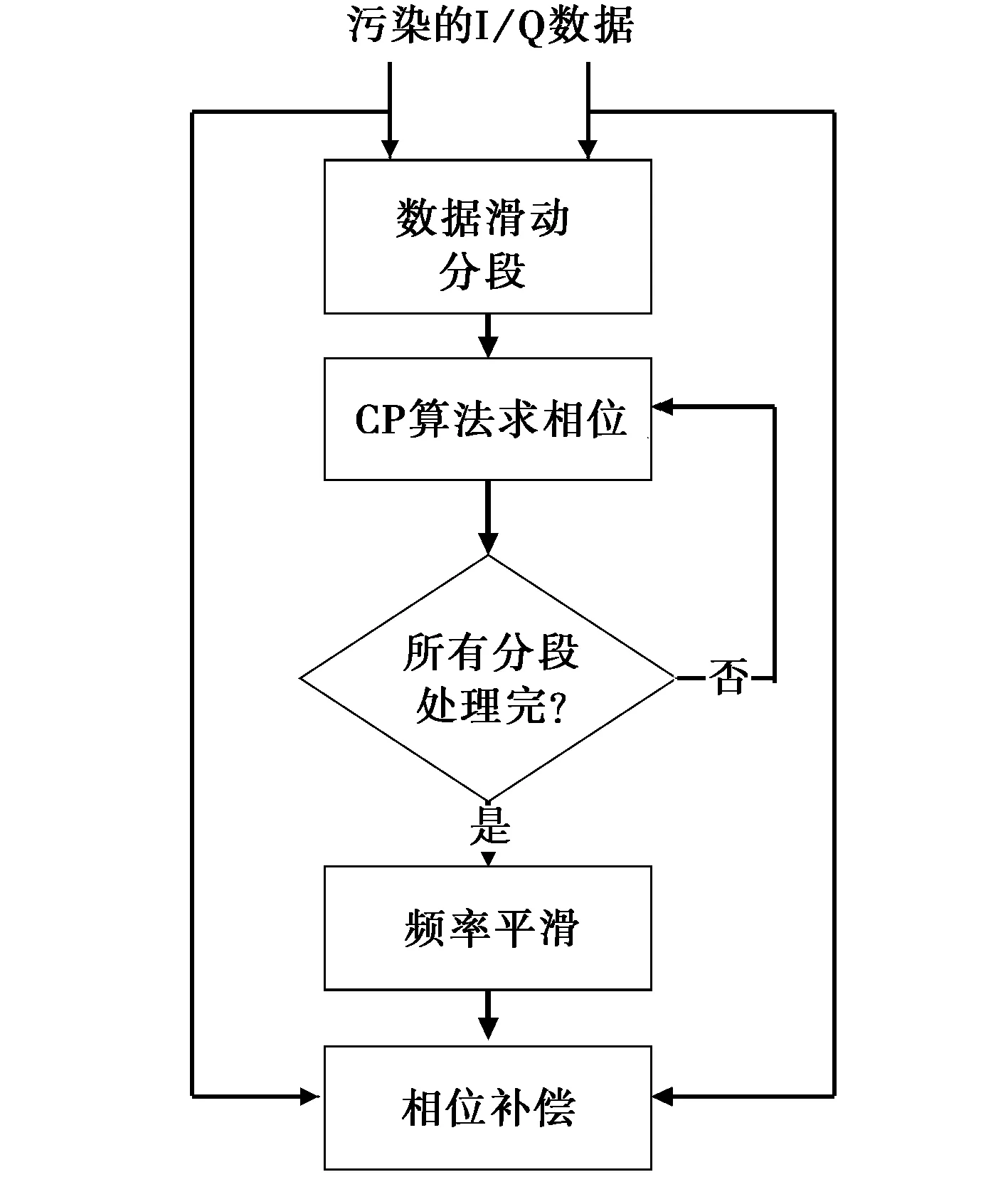
图1 基于CP的电离层污染补偿算法

1) 对某个距离单元一个CPI内的数据做FFT变换，将数据变换到频域。

2) 在给定频域区间进行谱峰搜索，滤出最强的谱峰，用于提取频率信息。

3) 对提取出的谱峰做IFFT将数据变换到时域，然后将数据分段，对每段数据求取瞬时相位，每段数据还可以有交叠以便对估计结果进行平滑。

4) 对每段所得到的频率数据进行平均，得到每个采样点的瞬时频率。

5) 利用瞬时频率对回波作校正。

4 仿真结果

本节将给出基于三次相位建模的污染校正仿真结果。其中雷达工作频率为15 MHz，雷达脉冲重复频率为5 Hz，积累256个脉冲数，则其相干积累时间为51.2 s.两个Bragg分量的幅度分别为5和15.杂噪比为25 dB，动目标多普勒频率为0.59 Hz，信噪比为8 dB.天波雷达回波被信号γ(t)所污染(即调制)，

γ(t)=ejB1cos(2πfm1t+θ0)

(23)

式中：B1=0.5；fm1=0.25.

仿真结果如图2～5所示。其中图2给出了被污染的某距离单元的回波频谱，可以看出，两个Bragg谱峰都被展宽了，并且掩盖了动目标的频谱，使得目标无法检测。将负的Bragg峰分离出来进行处理，用所提算法估计其瞬时频率，图3(见1061页)给出了基于所提算法的瞬时频率估计与理论值的比较。其中，每段数据的长度为16个数据点，每段数据有两点的数据重叠，因此，总共处理的数据为121段。从图3可以看出， 新算法能够很好的跟踪频率的变化，具有很好的频率估计性能。

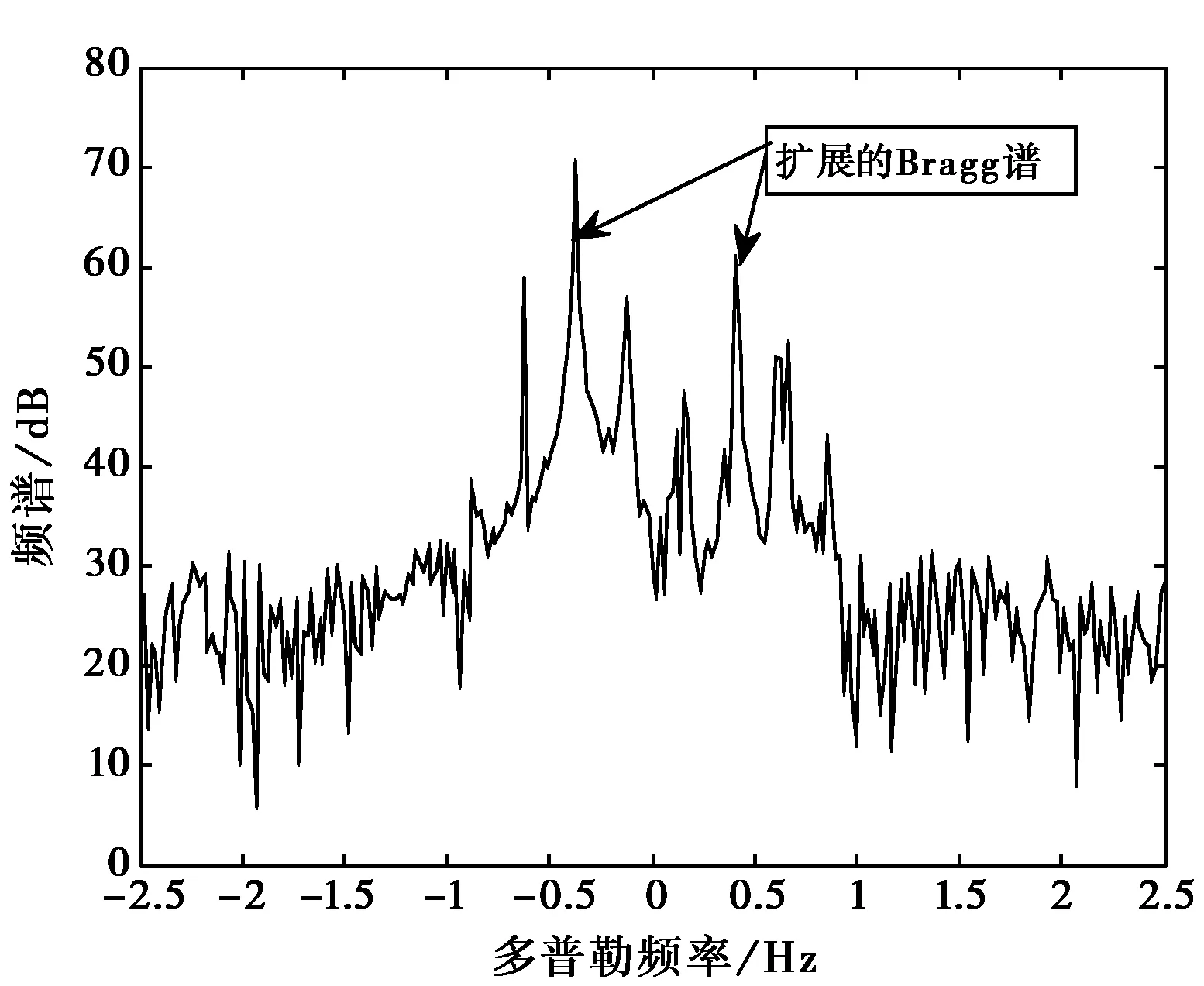
图2 被污染的天波雷达回波谱

图4是利用图3所得频率估计值进行补偿后的频谱。可以看出，经过补偿后，两个Bragg谱峰都变窄了，临近的目标很容易区分，证明算法具有较好的补偿效果。图5给出HRR算法补偿后的频谱。由于HRR算法在频率扰动较大时不能实现频率准确跟踪，因此，在此情况下，HRR算法不能实行有效的补偿。

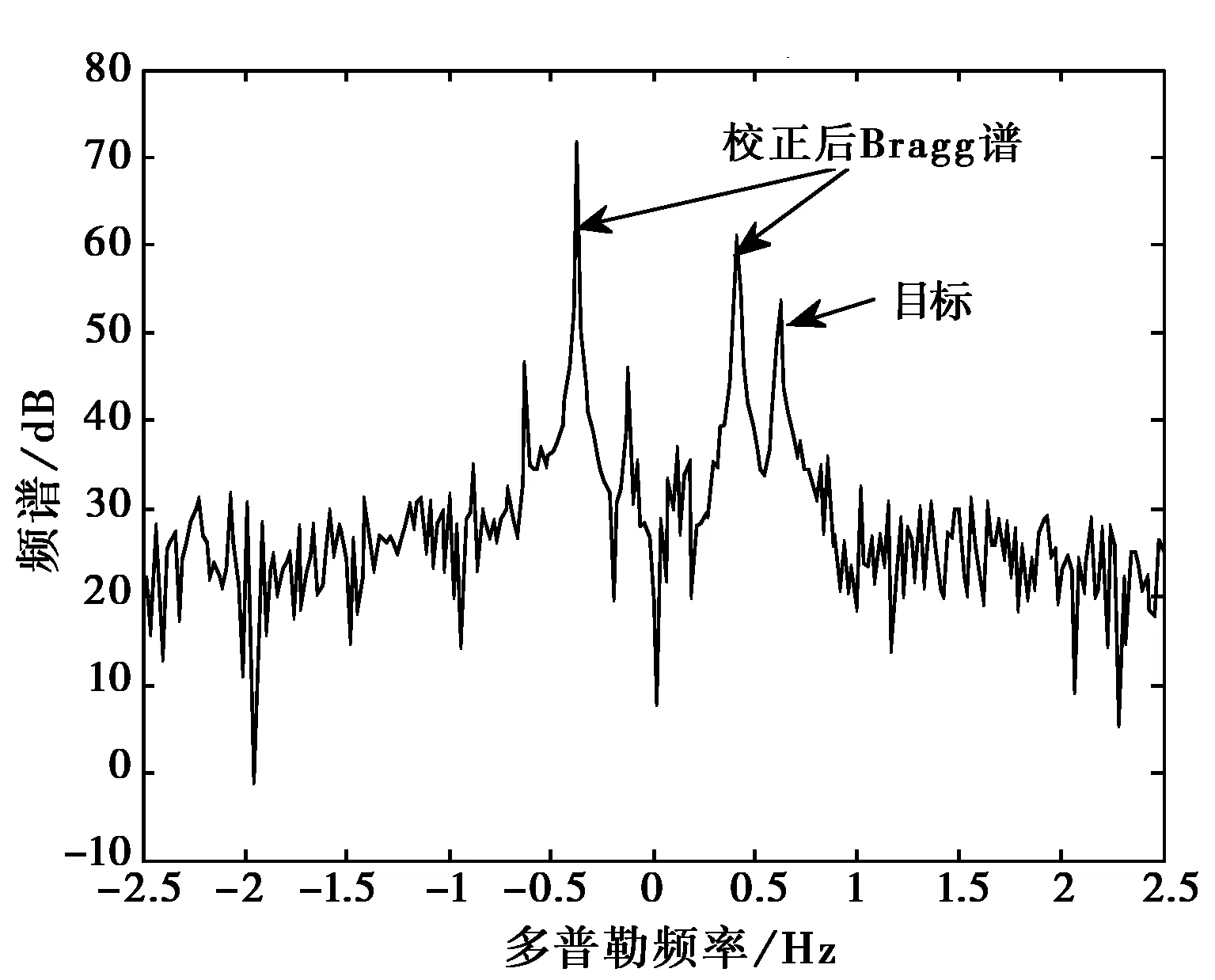
图4 新算法校正后的频谱

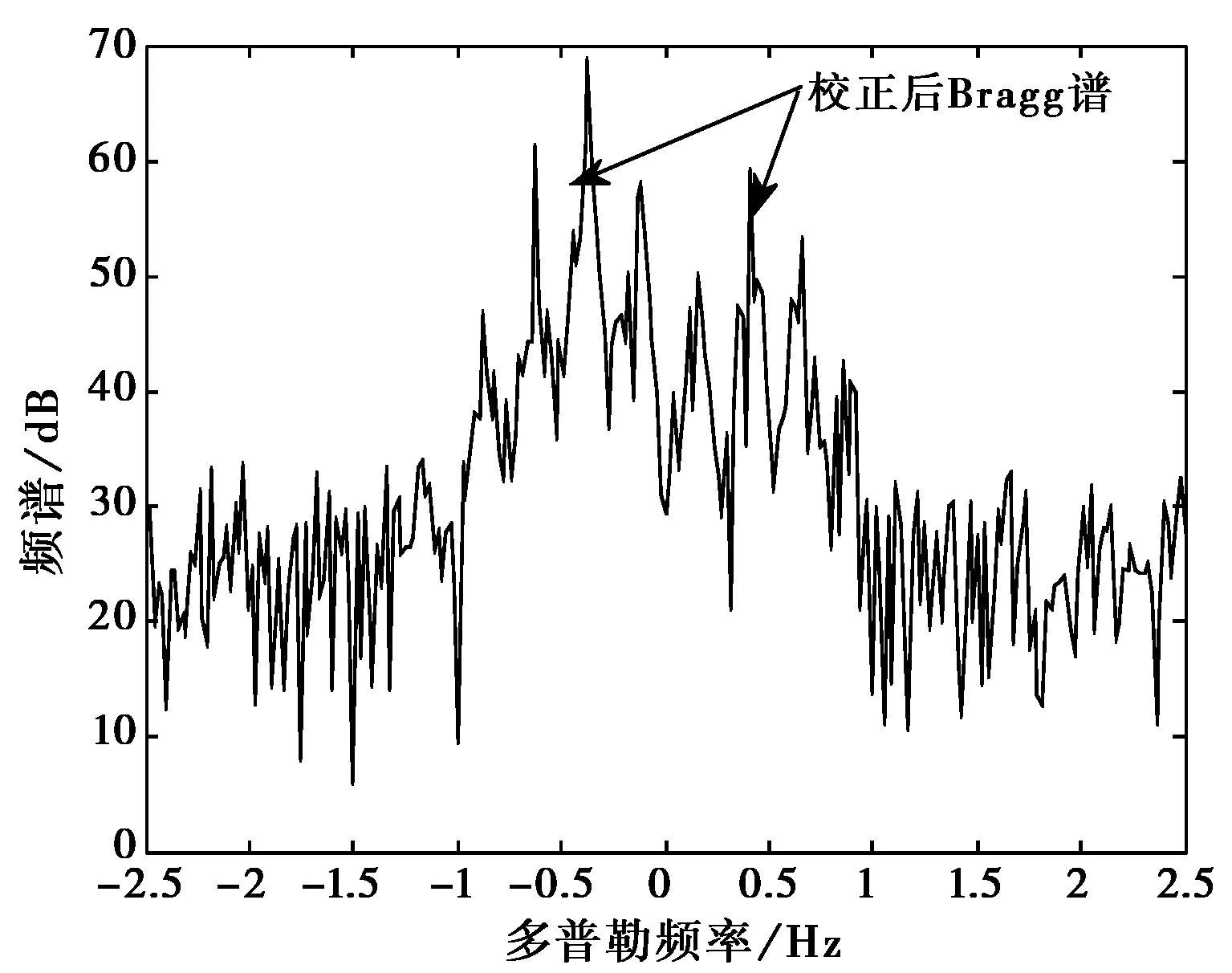
图5 HRR算法校正后的频谱

5 结 论

将三次相位信号用于对天波雷达的回波信号进行建模，在此基础上提出一种新的频率估计算法，并将所提算法应用于天波污染的校正。该算法的参数估计通过FFT进行，运算速度较快，仿真表明：对于一个256点的数据，算法可以在0.25 s左右完成校正处理。因此，所提算法可以进行实时处理。

另外，还给出了算法的具体流程及仿真结果。仿真结果表明：当天波污染较大时，所提算法比HRR算法频率估计要准确，因而具有更好的污染校正性能。

[1] 周文瑜, 焦培南. 超视距雷达技术[M]. 北京:电子工业出版社, 2008.

[2] 陈希信, 黄银河. 高频雷达回波信号去电离层污染[J]. 现代雷达, 2007, 29(2): 41-43.

CHEN Xixin, HUANG Yinhe. Ionosphere decontamination of high frequency radar echoes [J]. Modern Radar, 2007, 29(2): 41-43. (in Chinese)

[3] 苏洪涛, 刘宏伟, 保 铮, 等. 天波超视距雷达机动目标检测方法[J]. 系统工程与电子技术，2004, 26(3): 283-287.

SU Hongtao, LIU Hongwei, BAO Zheng, et al. Method for maneuvering target detection in HF over-the-horizon radar[J]. Systems Engineering and Electronics, 2004, 26(3): 283-287. (in Chinese)

[4] 周万幸. 天波超视距雷达发展综述[J]. 电子学报, 2011, 39(6): 1373-1378.

ZHOU Wanxing. An overview on development of skywave over-the-horizon radar[J]. Acta Electronica Sinica, 2011, 39(6): 1373-1378. (in Chinese)

[5] 姜 维, 邓维波. 分段多项式建模校正电离层相位污染算法研究[J]. 电波科学学报, 2011, 26(5): 855-863.

JIANG Wei, DENG Weibo. Ionospheric phase contamination correction method based on piecewise polynomial phase modeling[J]. Chinese Journal of Radio Science, 2011, 26(5): 855-863. (in Chinese)

[6] KHAN R. Ocean-clutter model for high-frequency radar[J]. IEEE Journal of Oceanic Engineering, 1991, 16(2): 181-188.

[7] 焦培南, 凡俊梅, 吴海鹏, 等. 高频天波返回散射回波谱实验研究[J]. 电波科学学报, 2004, 19(6): 643-648.

JIAO Peinan, FAN Junmei, WU Haipeng, et al. The experimental research of the Doppler spectrum by HF skywave backscattering[J]. Chinese Journal of Radio Science, 2004, 19(6): 643-648. (in Chinese)

[8] BAZIN V, MOLINIE J P, MUNOZ J, et al. NOSTRADAMUS: An OTH radar[J]. IEEE Aerospace and Electronic Systems Magazine, 2006, 21(10): 3-11.

[9] EARL G F, WARD B D. Frequency management support for remote sea-state sensing using the Jindalee skywave radar[J]. IEEE Journal of Ocean Engineering, 1986, 11(2): 164-172.

[10] BOURDLILLON A, GAUTHIER G. Use of maximum entropy spectral analysis to improve ship detection over-the-horizon radar[J]. Radio Science, 1987, 22(2): 313-320.

[11] PARENT J, BOURDLILLON A. A method to correct HF skywave backscattered signals for ionospheric frequency modulation[J]. IEEE Transaction on Antennas Propagation, 1988, 36(1): 127-135.

[12] HOWLAND P E, COOPER D C. Use of the Wigner-Ville distribution to compensate for ionospheric layer movement in high-frequency sky-wave radar systems[J]. IEE PROCEEDINGS-F, 1993, 140(1): 29-36.

[13] MARTIN W Y, KHAN R, SON L N. A singular value decomposition (SVD) based method for suppressing ocean clutter in high frequency radar[J]. IEEE Transaction on Signal Processing, 1993, 41(3): 1421-1425.

[14] LU K, LIU X Z, LIU Y T. Ionospheric decontamination and sea clutter suppression for HF skywave radars[J]. IEEE Journal of Oceanic Engineering, 2005, 30(2): 455-462.

[15] PELEG S, FRIEDLANDE B. The discrete polynomial-phase transforms[J]. IEEE Transactions on Signal Processing, 1995, 43(8): 1901-1914.

[16] 刘颜回, 聂在平, 赵志钦. 改进的分段多项式建模的电离层相位去污染新方法[J]. 电波科学学报, 2008, 23(3): 476-483.

LIU Yanhui, NIE Zaiping, ZHAO Zhiqing. A new method based on improved piecewise polynomial phase model to correct ionospheric phase contamination[J]. Chinese Journal of Radio Science, 2008, 23(3): 476-483.(in Chinese)

[17] 李 雪, 邓维波, 焦培南, 等. 多项式建模解电离层相位污染阶数选择新方法[J]. 电波科学学报, 2009, 24(6): 1094-1098.

LI Xue, DEND Weibo, JIAO Peinan, et al. Novel order-select method of polynomial modeling for ionosphere phase perturbation correction [J]. Chinese Journal of Radio Science, 2009, 24(6): 1094-1098. (in Chinese)

[18] 嘉德克 B K. 多项式一致逼近函数导论[M]. 沈燮昌, 译. 北京: 北京大学出版社, 1989.

[19] O’SHEA P. A fast algorithm for estimating the parameters of a quadratic FM signals [J]. IEEE Transactions on Signal Processing, 2004, 52(2): 385-393.