基于HHT算法的机械故障分析系统

吴 睿，万 舟，熊 新，汤占军

(昆明理工大学信息工程与自动化学院，云南 昆明 650500)

0 引 言

系统故障诊断主要是对系统运行状态和异常情况作出判断，并根据诊断结果寻求排除系统故障的依据，故障诊断技术的四个核心步骤是：信号采集、特征提取、模式识别和智能诊断，其中最难的步骤是采集故障信号和提取特征量.

机械设备在运行中的振动信号是反映其整体与变化规律的主要信号.因此，最时新的诊断方法是利用振动信号进行诊断.

在传统的信号处理中傅立叶变换是最常用的方法.虽然基于傅立叶变换的信号广泛应用于表述及分析离散时域信号领域，但是傅立叶变换只能从整体信号的时域表示得到其频谱，也就意味着只能完全在时域或完全在频域对信号的阐述，因此不能全面的描述信号同时在频域和时域中的变化，对信号的判断有一定的缺陷[1].而且傅立叶变换只能描述线性平稳信号的变换，而当旋转机械发生故障时的振动信号大多为非线性非平稳信号，其表示量(如功率谱等)也是时变函数.对于这种情况，只了解信号在时域或频域的瞬时特性是不够的，还需要得到信号频谱随时间变化的情况.为此，时频分析法就有了用武之地.

时频分析法可以在同一时间内提供振动信号的时域和频域的联合特征，主要反应出信号的局部特征，同时进行多尺度边缘检测，因此可对旋转机械的非平稳非线性故障例如动不平衡、不对中、动静碰摩等傅立叶变换难以有效分析的非平稳振动进行分析[2].时频分析法已广泛应用于旋转机械的故障诊断中.

时频分析即时频联合域分析的简称，其基本思想是设计时间和频率的联合函数，用它可以同时描述信号在时间和频率的能量密度或强度分布.由于这种分析方法提供了时间域与频率域的联合分布信息，所以我们可以清楚地了解信号频率随时间变化的关系.

希尔伯特-黄变换(Hilbert-Huang Transform，以下简称：HHT)是由美籍华人黄鄂等人于1998年提出，作为一种新型的经验模态分解时频分析法,其引入Hilbert谱的概念和Hilbert谱分析，这种对信号的处理方法可同时对信号的时域和频域进行分析，并且信号处理过程具有自适应性，非常适合处理非线性非平稳信号.因此，HHT变换在目前已知的机械故障诊断与非平稳信号处理上有很大的优越性.

本文主要研究基于LabVIEW平台的一套机械故障诊断系统，选用了HHT算法对故障信号进行分解和分析.

1 新型时频分析方法-HHT算法

HHT算法首先通过经验模态分解方法(Empirical Mode Decomposition，以下简称：EMD)对非平稳信号进行有效分解并得到一系列固有模态函数(Intrinsic Mode Function，以下简称：IMF)，然后每一个固有模态函数再通过Hilbert变换得到其瞬时频率和瞬时幅值，从而可得到Hilbert边际谱，具体流程图如图1所示.这样就有了对数据进行时频分析的依据， 并且从波形图中清晰地看出时间与频率的互相关系，从而合理的定义了瞬时频率及其物理意义，初步建立了以瞬时频率为基函数的新时频分析法系统[3].其中，EMD是最重要、最具创新性的部分.

图1 HHT算法流程图Fig.1 HHT flow chart

2 HHT算法的实现

EMD方法在Matlab平台实现较多，也有使用LabVIEW与Matlab结合实现的[4].本文针对LabVIEW工具箱中缺少EMD算法的问题，对LabVIEW进行二次开发，实现EMD的算法及HHT分析方法.

使用LabVIEW2010版，实现EMD程序(见图2)和HT(Hilbert Tromsform,以下简称：HT)程序(见图3).当信号进入程序时，首先进行三次样本拟合构造包络线，求出上下包络线；然后按IMF的取值条件之一——上下包络线的均值为零，对所求的信号的包络线进行判断，之后再进行EMD程序，其目的是消除载波与平缓不在要求内的幅值，本程序通过限定方差的大小在0.2～0.3之间来对所出信号进行筛选，其中，需要对剩余分量进行判断，判断标准为剩余分量已是单调函数，不可能再从中提取IMF分量，这样所得到的IMF分量再进入希尔伯特变换程序中，本程序使用到快速Hilbert变换作为分析主体程序，最终得到Hilbert变换波形图与Hilbert变换边际谱.

图2 EMD程序 Fig.2 EMD procedure

图3 HT程序Fig.3 HT procedure

利用仿真信号5sin(4π40t)+3sin(2π30t)+2sin(3π4t)对程序进行检验.采样数为1 000，采样频率为1 000 Hz，仿真信号波形图见图4.用HHT算法对仿真信号进行分析、分解得到3个IMF分量波形图(见图5).由图可见，IMF分量1是从仿真信号中分解出来的高频模态分量，对应了仿真信号公式中的第一个正弦函数部分；IMF分量2则是次高频模态分量，对应仿真信号中的第二个正弦函数部分；IMF分量3为分解后得到的次模态分量，其频率较低，幅度也很小，为仿真信号中第三个正弦函数部分.IMF分量4即为剩余分量，其值接近于0.由此可知，仿真信号得到了详细的分解，程序具有可靠的信号分解和时频处理能力.

图4 仿真信号波形图Fig.4 Simulation signal waveform

图5 仿真信号IMF分量波形图Fig.5 IMF components waveform of simulation signal

3 实验验证

采用能够模拟旋转机械故障的Bently模拟转子试验台，仿真转子的故障信号[5].信号采集卡采用NI公司生产的PCI-6251，此采集卡为16位，具有1 MS/s (多通道)和1.25 MS/s (单通道)两种通道形式，同时包括16路模拟输入、2路16位模拟输出(2.8 MS/s)、24条数字I/O线、32位计数器以及70多个信号调理选项关联DIO(8条时钟线, 10 MHz)[6]；其中所使用的模拟和数字触发NI-MCal校准技术和采用高精度M系列采集卡提高了测量精度、分辨率和敏感度.

压电传感器输出的原始信号经处理后的电压信号波形图见图6，各个IMF分量的波形图见图7，第一阶IMF分量和第二阶IMF分量对应的边际谱图见图8.

由图6、图7、图8可看出，HHT算法将动平衡故障所产生信号的固有模态分量分解出来.第一阶、第二阶IMF分量幅度较大，信号很杂，尤其第一阶IMF分量具有很明显的调幅特征，从第一阶IMF分量上更容易看出放大了的故障特征，证明高频成分的存在是由转子动不平衡造成.第三阶IMF分量为基频分量，第四阶IMF为剩余分量，幅值接近于0.在边际谱中看出，其幅值主要出现在频率的0～250 Hz与1750～2000 Hz之间.因此，图7、图8反映出来的故障特征符合转子动平衡的描述.

图6 原始电压信号波形图 Fig.6 Original signal waveform

图7 各个IMF分量波形图 Fig.7 IMF components waveform

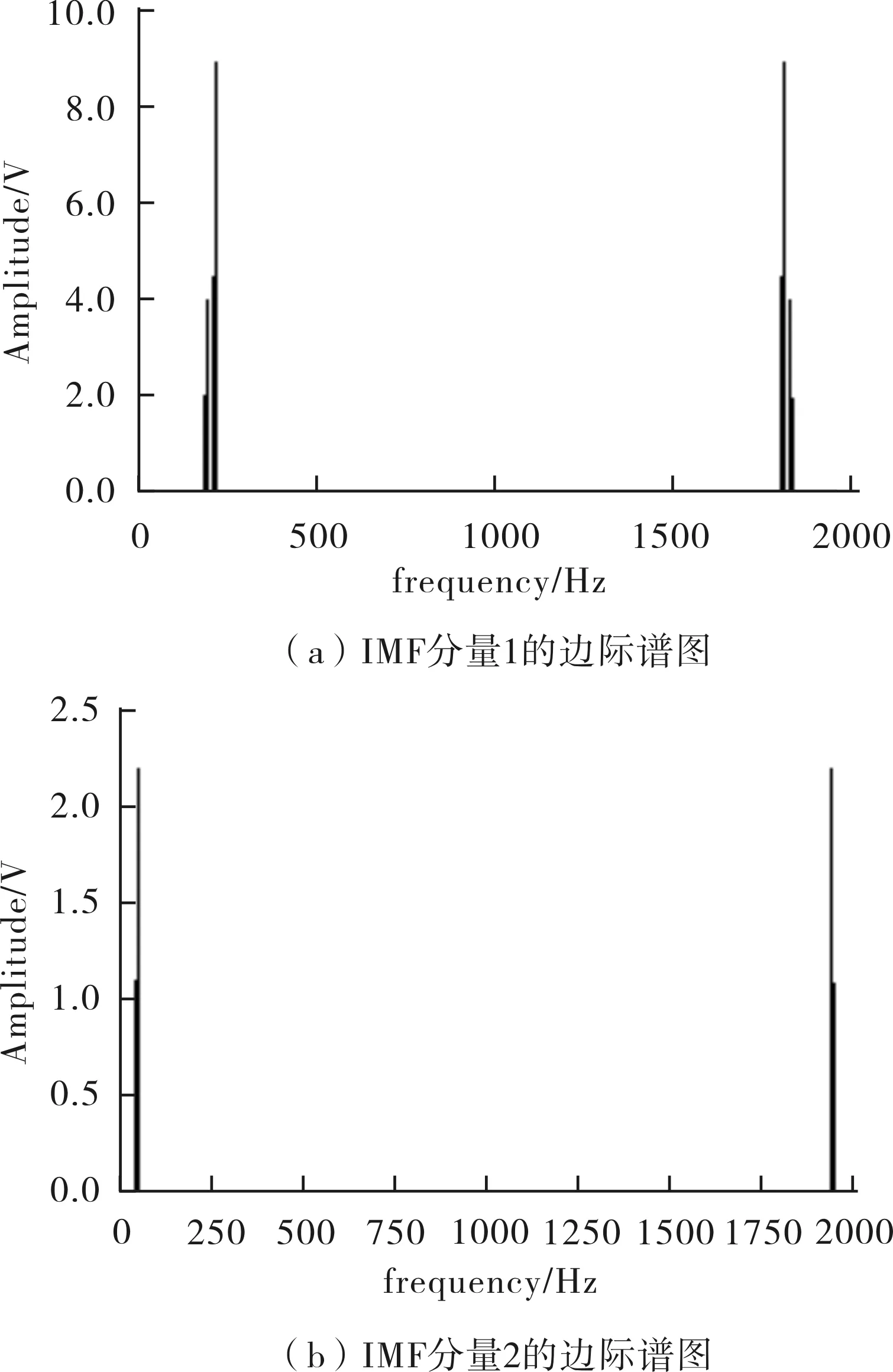
图8 HHT边际谱图Fig.8 HHT marginal spectrum

4 结 语

在LabVIEW平台下开发了“转子动平衡故障诊断系统”.通过在Bently转子实验台对转子动平衡进行分析试验,验证该系统是成功的、可靠的.在LabVIEW平台使用HHT算法能准确稳定的读取数据，并且可以通过对Hilbert谱的观察看出是否出现机械故障问题，若能把实时监测与数据储存方面结合到本系统中，其实际应用性将得到更大的提高.

参考文献：

[1] 谭宇硕.基于改进HHT方法的旋转机械故障诊断的研究[D].保定：华北电力大学,2007．

[2] 周月琴.机械设备状态检测系统设计及其信号处理算法研究[D].南京：南京信息工程大学,2008．

[3] 李博.基于LabVIEW的HHT方法实现及在轴承故障诊断中的应用研究[D].太原：太原理工大学,2008．

[4] 王珍，郭方，江亲瑜.EMD的LabVIEW实现及其在滚动轴承故障诊断中的应用[J].噪声与振动控制,2009(4):54-57.

[5] 迟万超，张方.基于LABVIEW的HHT法疲劳损伤时频分析[J].研究与开发,2011,30(7):34-38.

[6] 万书亭.基于机电综合特征的发电机转子故障诊断系统的研究[J].华北电力大学学报， 2007，34(6)：28-36.