基于优化的灰色GM模型的滑坡预测
2012-06-11李先福
肖 云,李先福
(武汉工程大学环境与城市建设学院,湖北 武汉 430074)
0 引 言
滑坡发生的时间预报,是目前滑坡预报的关键方向之一,也是滑坡灾害研究的主要目标[1].滑坡时间预测的核心之一就是滑坡预测模型的建立.滑坡形成机制复杂,其变形受多种因素影响,具有相当的模糊性和灰色不确定性,因而利用灰色预测模型对滑坡进行预测是一条有效的途径.灰色理论最常用的模型是GM(1,1),即1阶1个变量的微分方程型模型.该理论认为一切随机变量可视为一定范围内变化的灰色量,对该灰色量进行数据累加处理则相应生成的数据可淡化随机因素对原始数据的影响.灰色系统理论可以用来解决具有不确定关系的两因素间的问题,在滑坡地质灾害研究领域中已经得到了广泛的应用.
1 灰色GM模型原理
灰色理论是将已有数据序列经变换形成有规律的生成数列,建立灰色方程.将灰色方程的计算值与实际值进行比较,获得残差,同时检验模型的精度等级,当精度较低时需要利用残差对灰色预测模型进行修正,以满足精度要求,才能利用该模型进行预测[2].目前传统的GM(1,1)模型是应用最广泛的灰色模型之一,该模型是基于等时间距、由一个只包含一阶线性动态微分方程构成的模型.
1.1 GM(1,1)建模方法
设有给定的监测数据序列:
x(0)=(x(0)(t1),x(0)(t2),x(0)(t3),…,
x(0)(tn)) (x(0)>0)
x(1)=(x(1)(t1),x(1)(t2),x(1)(t3),…,
x(1)(tn))
(1)
(2)
若对x(1)(tk)建立灰微分方程:
x(0)(tk)+az(1)(tk)=b
(3)

式(3)GM(1,1)的白化灰微分方程转化为:

(4)
将式(3)写为向量积的形式,令Y= (x(0)(t2)x(0)(t3) …x(0)(tn))T,T表示转置.
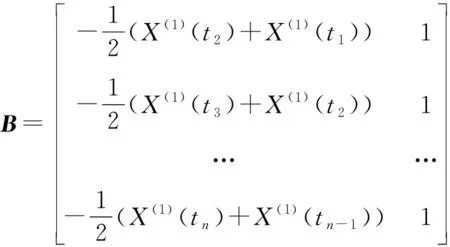
于是式(4)对应的时间响应序列方程为:
(5)

(k=1,2,3,…,n)
(6)
1.2 GM(1,1)模型适用范围
GM(1,1)模型是有偏差的指数模型,偏差是模型本身所固有的,其拟合精度和预测精度取决于常数a和b,用均值生成的z(1)tk+1)代替背景值,当时间间隔很小时,序列数据变化平缓时,这样的z(1)(tk+1)是合适的,模型偏差较小.当参数a值较小时,由偏差导致的误差较小,在一定的预测范围内,GM(1,1)模型可以使用.传统的GM(1,1)模型的具体适用范围如下[3]:①当-0.3 优化的GM(1,1)模型通过建立预测值与原实测值之差组成的残差序列来提高精度,对模型进行修正.而在运用残差模型修正提高精度时,最多不超过三次[4].计算表明,高级修正的精度高于低阶修正. 具体模型建立过程如下: 黄茨滑坡是位于甘肃省兰州市的一个典型的由灌溉引发的台缘滑坡[5].主滑方向为SE30度左右,前缘东西宽300 m,后缘东西宽近500 m,南北长370 m,体积近6×106m3.滑坡发育于黄河四级阶地的黑方台南缘,由于三级阶地缺失,该段台地边缘高出二级阶地100余米,均为陡坡和陡崖.四级阶地上部为大厚度黄土,达40余米,分两层.上部为20~30 m Q3的淡黄色黄土,结构松散单一;下部为厚10余米得Q2的棕红色黄土,水平层理清晰,结构致密.崖边伴生较为发育的垂直节理.黄土以下为数米厚的卵石层.阶地最下边为泥岩夹泥质砂岩,成单斜构造,倾向10~20度.1994年8月~1995年1月,铁道部科学研究院西北分院对其进行了长达半年的监测,积累了大量的监测资料,并对滑坡的发生作出了成功的预报. 2.2.1 传统GM模型研究 在短期和临滑预报阶段,滑坡位移时序变化已由不确定型向确定型或相对确定型转化,此时滑坡剧滑时间预报才具有现实意义和实现的可能[6].分析几种仪器设备所得数据可用于时间预测的有:地面监测桩、机械式自记单点位移计、电子式位移计[7].但地面监测网监测的数据精度低,监测间隔时间长,不适宜做临滑预报.机械式自记单点位移计测量各点的变形量,部分日位移量失真,A1、A2+A3、A4仅控制了一个裂缝带,它们的的监测资料不能全面真实的反映滑坡的动态,A6位移和A7数据可靠,可以说明滑体该部位的运动状态,特别是A7监测线跨越了后缘裂缝,所获得数据可充分说明滑体该部位的动态.电子记录式位移计取得的数据时间间隔较短,满足临滑预报模型时间的需求. 位移信息距离滑坡将要发生的实际时间越近,预测的精度越高,因此在做灰色预测分析时,选取机械式自记单点位移计A7和电子自记式单点位移计B2从1995年1月23~29日的观测数据进行计算分析,如表1. 表1 A7B2监测点位移数据 2.2.2 优化的GM模型 通过第一次预测值与实测值的残差比较,模型存在相当大的偏差,需要对模型进行改进,提出优化的GM(1,1)模型.经过一次修正后的GM(1,1)模型为: 26.4e0.000 714(tk-1-t1+20e0.000 465 8(tk-1-t1)-40 研究表明:当0<-a<0.3时,其预测精度在10步以内都在99%以上,由于所取数据均为临滑前数据,因此分析所得该模型完全可以边坡的用于短期的临滑预报. 2.2.3 优化GM(1,1)模型与传统GM(1,1)模型的预测精度比较 研究发现,未经过优化时,平均相对残差为28.58%;经过修正后,平均相对残差为0.19%.说明经过修正后优化的GM(1,1)模型其预测精度比传统的GM(1,1)模型要大大提高. 2.2.4 B2单点的GM(1,1)模型研究 分析B2单点的预测模型: 计算得到预测值与实测值进行比较,判断其精度是否符合数据需求.计算其残差,预测精度如表2. 表2 预测值与实测值的比较Table 2 Comparison of predicted and measured values 因此该模型: 2.2.5 滑坡临滑预报研究 由于滑坡体上不同部位的变形-破坏发展趋势不同,本次研究由于不同仪器监测数据的优选和数据来源问题,仅选取滑体后缘临滑前两组数据(B2点的预测曲线与实测曲线对比图如图1).根据曲线的翘尾判据,大量的滑坡监测资料分析,往往在89~89.5度之间的斜率所对应的时间为滑坡剧滑时间危险段.本次所做模型由于取值的原因,只记载有以天为单位的位移量,因此在曲线的翘尾阶段,应作出临滑预报.从图1中可以看出,t0时刻以后,位移时间曲线近似陡直,因此判断为t0值为滑坡破坏的临界拐点值,滑坡自此进入破坏失稳阶段,t0对应的时间为1月29日,以后位移曲线突变陡直[8]. 黄茨滑坡实际滑动时间为2月1日凌晨3时左右,预测时间稍微偏小,可以起到提前预报作用. 图1 B2监测点推导的预测曲线与实测曲线对比图Fig.1 Comparison of predicted and measured curve of B2 本次研究采用灰色优化的GM(1,1)模型时,与实际吻合良好. a.在系统监测的基础上,选取监测数据时应该合理选用多种监测手段的数据进行综合分析,准确判断长期、短期和临滑预报阶段滑体变形规律,根据有效监测数据选择合适的预测模型. b.由于滑坡体上不同部位的变形-破坏发展趋势不同,对滑体进行预测预报应该尽量选取滑体不同部位的监测数据进行预测分析.本次研究由于不同仪器监测数据的优选和数据来源问题,仅选取滑体后缘临滑前两组数据. c.基于位移信息的GM(1,1)灰色模型所作的临滑预报,采用的监测数据应该尽可能临近滑坡发生的时间,才能保证更高的预测精度.本次所做模型由于取值的原因,只记载有以天为单位的位移量,因此在曲线的翘尾阶段,处于临滑阶段的位移-时间曲线呈现急剧上升的趋势,应作出临滑预报. d.本文研究根据所取点的优化GM(1,1)模型,从图中预测位移值与实际的实测值对照可以看出,模型拟合度比较高,并且根据翘尾阶段做出的临滑时间判断与实际吻合,可以起到提前预报作用. e.由于滑坡形成机制复杂,边坡变形受多种因素影响,坡体呈现出不同形式的变形破坏,对于不同的滑坡,甚至是大块的崩塌或塌陷等,要探讨其变形发展特征,不能千篇一律采用统一的模型.不同的预测模型计算,预测结果会因所选取的数据的不同而造成差异.在预测预报时,应该综合选用不同的预测模型进行预报结果分析. 参考文献: [1] 殷坤龙.滑坡灾害预测预报[M]. 1版.武汉:中国地质大学出版社,2004:52-53. [2] 李克钢.岩质边坡稳定性分析及变形预测研究[D].重庆:重庆大学,2006,6. [3] 黄润秋,许强.滑坡预测模型及预报判据研究[R].2004,7:36. [4] 邓聚龙.灰色预测与决策[M].武汉:华中理工大学出版社.1988. [5] 温文,吴旭彬.Vethulst模型在黄茨滑坡临滑预测中的应用[J].人民珠江,2005,5:39-40. [6] 徐峻龄,廖小平,李荷生.黄茨大型滑坡的预报及其理论和方法[J].铁道工程学报,1996,50(2):197-198. [7] 毛广湘.黄茨滑坡预测预报分析[J].建筑科学,2003,23(3):31-32. [8] 肖云,周春梅,虞珏,等.大冶铁矿滑坡预测模型研究[J].武汉工程大学学报,2010,32(1):9-11.1.3 灰预测的检验
1.4 优化GM(1,1)模型的建立
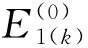


2 工程实例
2.1 黄茨滑坡概况
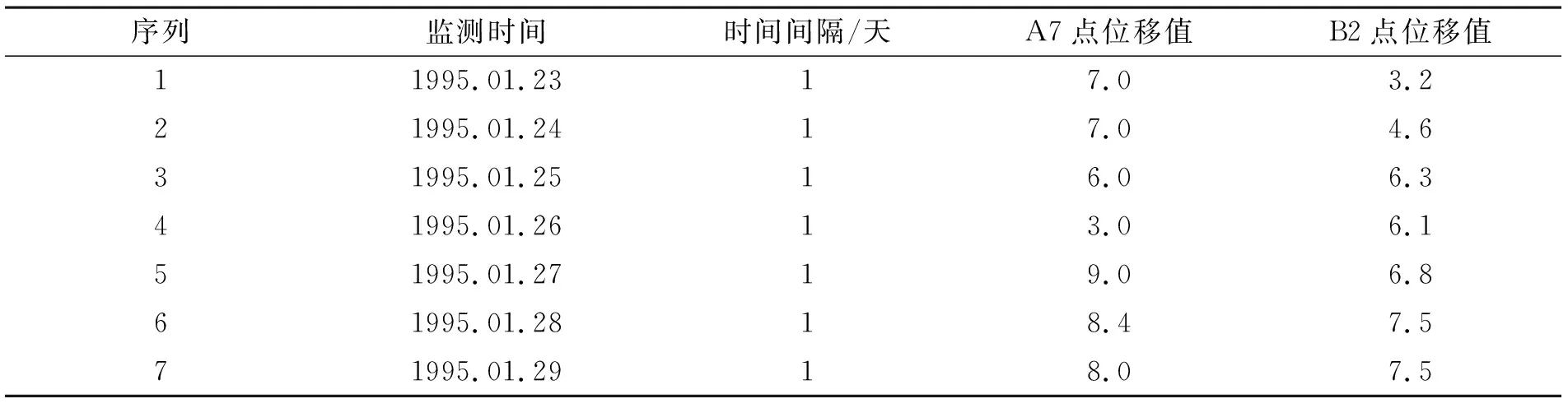
2.2 黄茨滑坡灰色预测模型研究
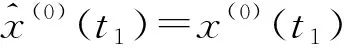




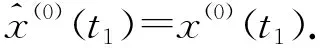
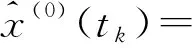


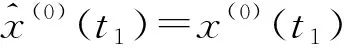

3 结 语
