可靠通信的多跳水声网络能量最小路径*

王 琛，方彦军

(武汉大学自动化系，武汉430072)

近年来，随着人类海洋活动的日益频繁，水声传感器网络以其在海洋资源勘探、环境监测以及军事防御等众多领域的应用潜力，引起了国内外研究学者的广泛关注[1－3]。由于水声网络的节点通常由电池供电，而目前水下充电技术尚不成熟，且在水下大范围更换电池成本太高，因此降低节点能耗以延长网络生命期就显得尤为重要。

目前已有许多针对降低水声网络能耗的路由协议和 MAC(Medium Access Control)协议被提出[4－8]，但并未重视水声信号的传播特性。文献[9]在分析水声信号传播特性后指出，多跳模式可以有效减少节点功耗，同时能增加可用带宽，有望成为下一代水声网络的组网策略;在此基础上，文献[10]指出直线等距的多跳网络模型相对于二维或三维模型能耗更低，但并未给出理论证明。与之类似的问题在无线传感器网络中也有研究，如文献[11－12]分别证明了AWGN信道和多跳网络的总能耗在直线等距的拓扑下最低。

不过，与陆地无线信道相比，水下信道的传输条件要恶劣得多，数据包在传输过程中发送失败、丢包等情况更为频繁[13]，为保证水下网络的可靠通信，通常会有链路层的恢复机制(如检错重发或使用前向纠错码等)，由此而带来的能耗在前述对能量最小路径的研究中并未考虑。

本文通过建立可靠通信的多跳水声网络能耗模型，研究给定接收信噪比条件下的网络能量最小路径问题，证明了可变发送功率和固定发送功率两种模式下，直线等距网络的总能耗最小，并给出最优跳数和最优距离的求解方法。

1 系统模型

1.1 水声传播损失与噪声

根据Urick的传播模型[14]，频率为 f kHz的水声信号传输距离d km时的传播损失A(d，f)的分贝形式为:

等式(1)右边第1部分为扩展损失，第2部分为衰减损失。式中dref为参考距离(通常取值为1 m)，κ为衰减因子(一般介于1到2之间);α(f)为频率性的吸收系数(单位为dB/km)，可通过Thorp公式[15]得到。在某些较低的频率区域，α(f)常由下面的经验公式获得[16]:

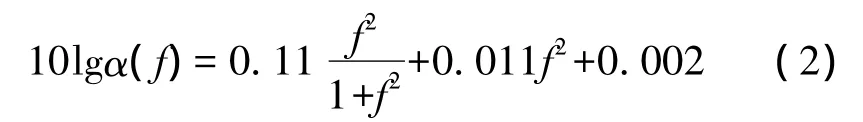
水下环境噪声受潮汐、湍流、海面的风浪、船舶扰动及热噪声等多种因素的影响，其功率谱密度N(f)随载波频率的升高而降低，在特定的频率区间可采用如下经验公式近似表示[16]

其中 N0=50 dB re μ Pa，η=18 dB/decade。

本文假设 κ=1.5，α(f)和 N(f)分别由式(2)和式(3)计算得出。

1.2 多跳网络模型

考虑一个二维多跳网络模型，源节点和目的节点相距为D，通过任意分布的K－1个中继节点进行数据通信(如图1所示)。源节点用N0表示，目的节点用Nk表示，中继节点表示为Ni，i=1，…，K－1，其中K 为跳数。采用文献[17]中的表示，设第i条链路的距离di满足di=φiD，不难得出(其中代表直线路径)。

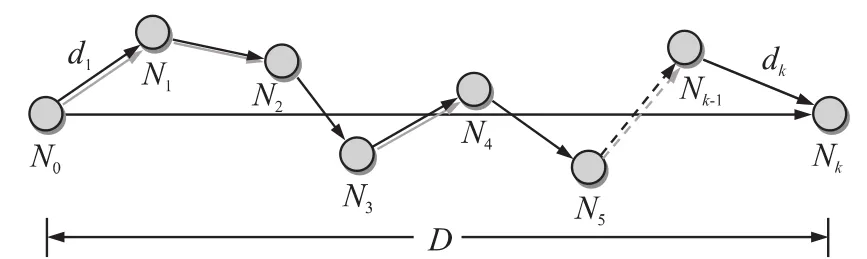
图1 二维多跳网络模型

对此网络模型做如下假设:(1)节点只能半双工通信，这意味着节点不能同时处于发送和接收状态;(2)链路的连通性仅限于相邻的两个节点之间，因此不考虑节点间的合作机制以及网络的空间重用;(3)节点可以选用固定发送功率和可变发送功率两种模式，但同一网络中各节点所用模式相同;(4)每个节点都具备检错重发数据的功能。

1.3 可靠通信的能量模型

一条链路传输一个数据包所需的能耗E包括发送数据包的能耗Et和接收并处理数据包的能耗Ec:

Et可通过发送功率Pt乘以发送时间得到，L为数据包长(单位bit)，ρ为调制带宽效率(单位bit/s/Hz)，B(d)为可用带宽(单位 kHz)，随距离的增加而变小[10]。对于给定的目标接收信噪比γtgt，

其中ξ是声功率(单位为dB re μ Pa)转换为电功率(单位为 Watt)的转换系数。

Ec与链路的距离无关，且通常远小于Et，因此本文假设Ec为固定值。则式(4)可转化为

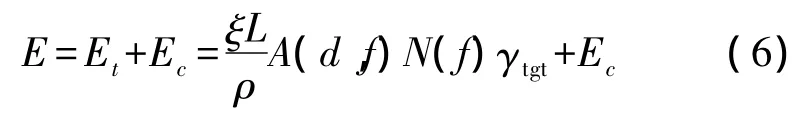
若设链路误包率为p，则确保数据包传输成功所需的发送次数是一个几何分布的随机变量，且平均发送次数为1/(1－p)[18]。因此，链路可靠传输一个数据包的能耗

2 AN积的简化

从式(7)可以看出，链路可靠传输的能耗主要取决于A(d，f)N(f)(简称AN积)，其包含传输距离d和信号频率f两个变量，研究起来比较复杂。本节将研究AN积的性质，寻求f和d之间的关系，以便简化计算。

2.1 AN积的性质

由式(1)～式(3)可得出分贝形式的AN积:

图2画出了不同传输距离时的AN积与信号频率的关系。从图2可以看出有如下性质。

图2 不同传输距离时的AN积与信号频率的关系

性质1对于给定的传输距离d，存在一个最优频率fo(d)使AN积最小，即

证明 将ANdB对f求导，其一阶导数满足

故存在频率f=fo(d)使

此时ANdB达到最小值。证毕。

2.2 d与fo(d)的关系

性质1表明，距离为d的链路采用fo(d)作为信号频率时AN积最小。若能得出d与fo(d)的函数关系，则可将式(7)转化为仅含d一个变量的表达式。为此，将ANdB对d求导，并令其一阶导数为零

从上式无法得到fo(d)关于d的闭式解。为此，将上式的数值解通过MATLAB曲线拟合得到两个拟合度较好的曲线 fo(d)=adβ和 fo(d)=adβ+χ，其参数见表1，其中SSE(Sum of Squares due to Error)为和方差，RMSE(Root Mean Squared Error)为均方根。注意到式(12)中f均为偶次方幂，而拟合曲线中参数β与0.5十分接近，因此我们采用如下函数作为拟合曲线以简化计算:

表1 最优频率拟合曲线及其参数

其 SSE 为2.6207，RMSE 为0.2196。图3给出了该曲线(实线)与数值解(圆圈)的示意图，从图3可以看到，该曲线拟合度令人满意。

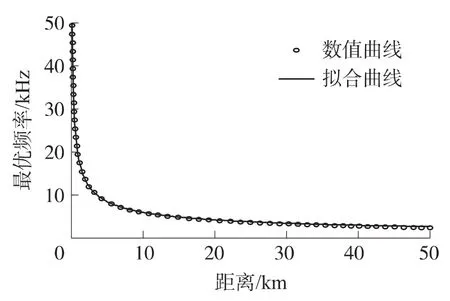
图3 最优频率与距离的关系

2.3 AN积的简化表达

将式(13)代入式(8)即可得到

注意到g(d)是d的单调递增函数，因为g'(d)＞0。

3 能量最小路径分析

本节利用第2节得到的AN积的近似表达式来分析可变发送功率VTP(Variable Transmission Power Strategy)和固定发送功率FTP(Fixed Transmission Power Strategy)两种情况下的能量最小路径。

在可变功率情况下，节点通过调整发送功率以保证信号到达目的节点时有相同的目标接收信噪比γtgt。在此情况下，若各链路信号频率变化不大时，传输距离越大的链路需要越高的发送功率。

在固定功率情况下，各节点的发送功率相同。为保证各链路的接收信噪比不低于γtgt，此时各链路的发送功率应选择AN积最大链路的发送功率。尽管与可变功率相比，固定功率对能量的利用效率明显较低，但对其研究也是必要的，因为目前大部分水声节点不具备调节发送功率的功能。

3.1 可变功率的能量最小路径

由式(7)，链路i的可靠传输能耗

则网络可靠传输的总能耗为

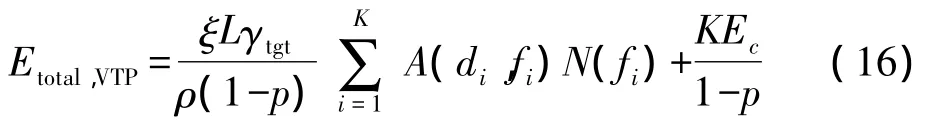
将近似的AN积代入，则可变功率的能量最小路径问题可以转化为以下优化问题:

其中变量为di。该优化问题的解由以下定理给出。

定理1对于节点任意分布的多跳水声网络，若各节点采用可变功率模式，且各链路接收信噪比不低于给定的目标接收信噪比，则直线等距路径使可靠传输的网络总能耗最小。

证明 构造该优化问题的拉格朗日函数

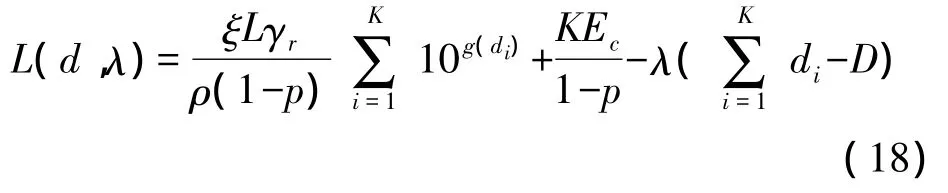
其中 λ≥0 为拉格朗日乘子，d=(d1，d2，…，dK)。则其KKT条件(Karush-Kuhn-Tucker Condition)为:

由第1组优化条件可知，对任意的i，Χ(di)=10g(di)·g'(di)为固定值，由 Χ(d)=10g(d)·g'(d)的单调性(Χ'(d)＞0)可知 d1=d2=…=dK，为等距网络;同时，第一组条件表明λ0，因此不难从第2个条件得出，为直线网络;进而可得KKT对，其中 λ*可由式(19)得出。另一方面，考察其切空间中的任意 y≠0，有 yTH(d*，λ*)y＞0，其中H(d*，λ*)为该优化问题的拉格朗日函数在(d*，λ*)处的 Hesse矩阵[19]，故能保证 KKT 条件的充分性。综上可知，直线等距网络能使可变功率情况下的网络能耗最小。证毕。

3.2 固定功率的能量最小路径

固定功率情况下，链路i的能耗取决于所有链路中AN积最大链路的能耗，即

由于各链路发送功率相同，因此可靠发送一个数据包的总能耗

将近似的AN积代入，则固定功率的能量最小路径问题可以转化为以下优化问题:

其中变量为 dmax。该优化问题的解由以下定理给出。

定理2对于节点任意分布的多跳水声网络，若各节点采用固定功率模式，且各链路接收信噪比不低于给定的目标接收信噪比，则直线等距路径使可靠传输的网络总能耗最小。

证明 不难看出，Etotal，FTP是关于dmax的单调递增函数，因此式(22)与下面的式子等价:

因为 di≤dmax，所以;而，则Kdmax≥D，故，即

此即表明直线等距网络能使固定功率情况下的网络能耗最小。证毕。

3.3 最优跳数与最优距离

既然可靠通信的能量最小路径是直线等距网络，那么自然需要考虑一个问题，即各节点相距多少能使能耗最少?也就是，使能耗最小的最优跳数是多少?

因此，考虑直线等距网络的总能耗

把K视为连续量，将上式对K求导并令其一阶导数为零可得

若令d*为方程的解，则最优跳数

其中k*为自然数，d*可通过数值方法求得。此时网络的最优能耗为

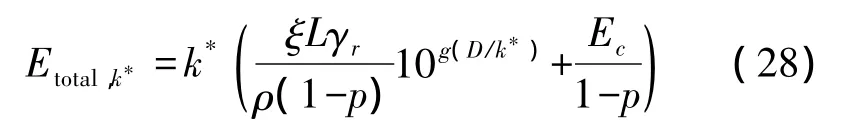
4 仿真结果

本节对第3节的定理进行验证，并对直线等距网络的最优跳数和最优距离进行仿真。仿真中只考虑直线网络的情况(即)，因为在同样的节点分布时非直线网络能耗显然更高。仿真试验的参数设置如下:误包率 p=0.1，调制带宽效率 ρ=0.5，声－电功率转换系数 ξ=4×10－17，数据包长度 L=256 byte，接收能耗Ec=0.5 J，目标接收功率信噪比 γtgt=20 dB。

图4比较了不同节点位置时可变功率和固定功率模式下的能耗与距离的关系。从图中可以看出，不论是2跳或是3跳网络，等距时的能耗最低，这与第3节的理论相符。同时可以看出，当节点位置相同时，固定功率模式较可变功率模式能耗更高，这是由于固定功率模式下，各链路发送功率均选择AN积最大链路的发送功率，以牺牲能耗为代价来证各链路的接收信噪比不低于γtgt。

图4 不同节点位置时能耗与距离的关系比较

图5描绘了直线等距网络在传输距离从10 km到100 km时总能耗与跳数的关系。从图中能明显看出，对不同的传输距离，存在一个最优跳数使总能耗最低，且距离越长，最优跳数越大。

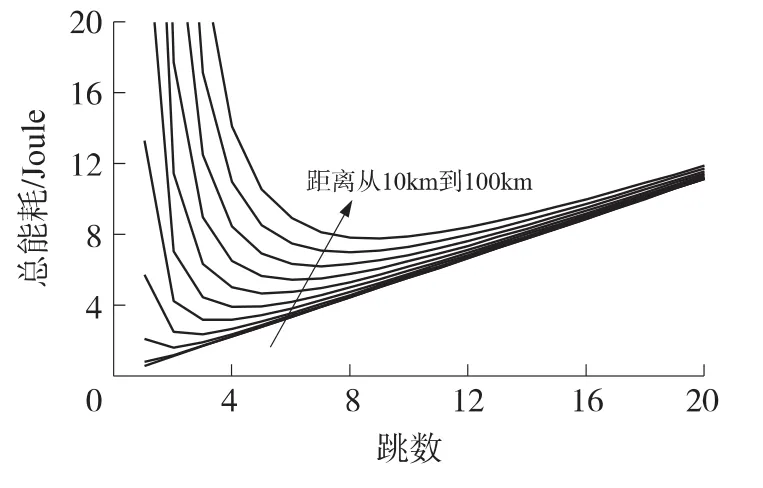
图5 直线等距网络在不同距离时总能耗与跳数的关系

图6给出了直线等距网络在跳数从1到12时总能耗与传输距离的关系，可以看出，在某一段距离区间内，存在一个最优跳数使总能耗最低，且相邻跳数的总能耗与跳数关系曲线之间的交点(小圆圈)，其连线近似为一条直线，印证了式(27)中最优跳数与最优距离近似的线性关系，而相邻交点间的距离也近似相等(约13 km)，即为最优距离。

图6 直线等距网络在不同跳数时总能耗与距离的关系

此外，从图4～图6都能看出，在较短传播距离(k＜15 km)时，单跳较多跳能耗更低，这也说明并非任何情况下都是多跳能耗更优。

5 结束语

本文研究了可靠传输条件下多跳水声网络的能量最小路径。建立了二维的网络能量模型，通过曲线拟合的方法得到了最优频率－距离的近似表达式，并利用该表达式分析了可变功率和固定功率两种模式下的能量最小路径。结果表明，无论对于可变功率还是固定功率的多跳水声网络，其可靠传输时直线等距网络能使总能耗最小。考虑直线等距网络，本文还给出了使能耗最小的最优跳数和最优距离。所得结果对于近岸环境监测网络的实现有一定的指导意义。

[1]Heidemann J，Mitra U，Preisig J，et al.Underwater Wireless Communication Networks(Guest Editorial)[J].IEEE Journal on Selected Areas in Communications，2008，26(9):1617－1619.

[2]吕超，王硕，谭民.水下移动无线传感器网络研究综述[J].控制与决策，2009，24(6):801－807.

[3]郭忠文，罗汉江，洪锋，等.水下无线传感器网络的研究进展[J].计算机研究与发展，2010，47(3):377－389.

[4]钟永信，黄建国，韩晶.基于空间唤醒的水声传感器网络节能路由协议[J].电子与信息学报，2011(6):1326－1331.

[5]Lee U，Wang P，Noh Y，et al.Pressure Routing for Underwater Sensor Networks[C]//IEEE INFOCOM，San Diego，CA，USA，2010:1－9.

[6]刘玉梁，潘仲明.水下无线传感器网络能量路由协议的仿真研究[J].传感技术学报，2011，24(6):905－908.

[7]王锦程，李德识.一种基于水声信道的无线传感器网络路由协议[J].传感技术学报，2009，22(1):107－110.

[8]Park M K，Rodoplu V.Uwan-Mac:An Energy-Efficient Mac Protocol for Underwater Acoustic Wireless Sensor Networks[J].IEEE Journal of Oceanic Engineering，2007，32(3):710－720.

[9]Stojanovic M，Preisig J.Underwater Acoustic Communication Channels:Propagation Models and Statistical Characterization[J].IEEE Communications Magazine，2009，47(1):84－89.

[10]Zorzi M，Casari P，Baldo N，et al.Energy-Efficient Routing Schemes for Underwater Acoustic Networks[J].IEEE Journal on Selected Areas in Communications，2008，26(9):1754－1766.

[11]Bae C，Stark W E.On Minimum Energy Routing in Wireless Multihop Networks[C]//Information Theory and Applications Workshop，San Diego，CA，USA，2009:346－350.

[12]Zhang R，Gorce J M.Optimal Transmission Range for Minimum Energy Consumption in Wireless Sensor Networks[C]//IEEE Wireless Communications and Networking Conference(WCNC)，Las Vegas，Nevada，USA，2008:757－762.

[13]Liu L，Zhou S，Cui J H.Prospects and Problems of Wireless Communication for Underwater Sensor Networks[J].Wireless Communications and Mobile Computing，2008，8(8):977－994.

[14]Urick R J.Principles of Underwater Sound[M].New York:McGraw-Hill，1983.

[15]Berkhovskikh L，Lysanov Y.Fundamentals of Ocean Acoustics[M].New York:Springer，1982.

[16]Stojanovic M.On the Relationship between Capacity and Distance in an Underwater Acoustic Communication Channel[J].ACM SIGMOBILE Mobile Computing and Communications Review(MC2R)，2007，11(4):34－43.

[17]Bae C，Stark W E.End-to-End Energy-Bandwidth Tradeoff in Multihop Wireless Networks[J].IEEE Transactions on Information Theory，2009，55(9):4051－4066.

[18]Banerjee S，Misra A.Minimum Energy Paths for Reliable Communication in Multi-Hop Wireless Networks[C]//ACM International Symposium on Mobile Ad Hoc Networking ＆ Computing(MobiHoc)，EPFL Lausanne，Switzerland，2002:146－156.

[19]Borwein J M，Lewis A S.Convex Analysis and Nonlinear Optimization:Theory and Examples[M].Springer Verlag，2006.