大噪声环境下频率响应函数测量研究*

唐 炜，包 斌，乔 倩

(西北工业大学自动化学院，西安710072)

测量结构的频率响应函数是模态实验的重要内容，现有大多数频域模态识别方法多以频响函数为基础，其准确程度直接影响了识别结果。但是，在某些场合下，当采用人工激励进行模态实验时，还不可避免会受到自然环境激励的影响。例如，飞行中的飞机在进行颤振试飞时还会受到大气紊流的激励，在这类情况下，不可测的自然激励引起的结构响应将作为噪声被包含在实验数据中，严重降低实验数据的品质，进而引起频响函数估值不准。因此，研究大噪声下频响函数测量[1－3]是一个颇为重要的问题。

目前国内外已有多篇文献涉及该领域研究[4－7]，它们均将采用扫频信号作为激励源，进行模态实验。其目的是利用扫频信号聚焦于时频域特定区域，而噪声则广泛分布于整个域内的特性，实现信噪分离。其中，文献[5]最早提出了采用小波时频分析进行去噪处理，并成功应用于美国F－18试验机的颤振试飞数据处理。受此启发，基于分数阶傅里叶变换，作者曾提出了一种广义时频滤波算法[6]，相比于文献[5]中采用的小波方法，分数阶傅里叶变换能够更加有效的去除噪声。但是该方法是针对实数实验数据进行滤波，在分数阶傅立叶域内易发生混叠，一定程度上影响了该方法的去噪效果。

为此，本文在文献[6]基础上，提出了一种大噪声环境下频响函数测量的改进方法。其不同之处在于，运用两次实验数据构造了“虚拟”的复数扫频信号，可以避免采用实数数据进行分数阶傅里叶变换时易发生的混叠问题，进一步提高去噪效果和频响函数的测量精度。

1 分数阶傅里叶变换

分数阶傅里叶变换，作为傅里叶变换的广义形式，信号的FRFT[8－10]可以解释为将信号的坐标轴在时频平面上绕原点作逆时针旋转。如图1所示，信号的傅里叶变换可看成将其由时间轴上逆时针旋转π/2后到频率轴上的表示。则p阶的FRFT可以视为将信号在时间轴上逆时针旋转角度α(α=pπ/2)到u轴的表示(u轴为分数阶傅里叶域)，因此，可将FRFT看作由变换矩阵定义的线性变换:

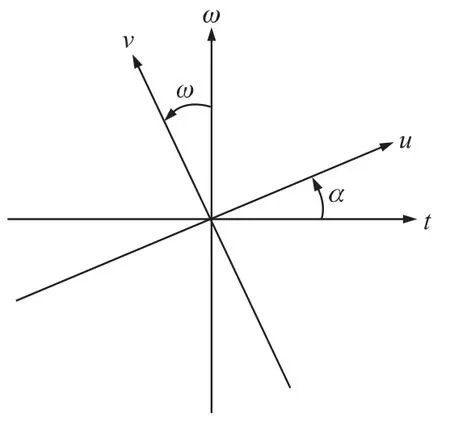
图1 分数阶傅里叶变换的时频域旋转表示

从本质上讲，信号在分数阶傅里叶域上的表示，同时融合了信号在时域和频域的信息，因此，FRFT被认为是一种广义时频分析方法。信号x(t)的p阶傅里叶变换可定义[9－10]为

其中分数阶傅立叶变换核为:

式中Fp为分数阶傅立叶变换的算子符号，p为分数阶傅立叶变换的阶，可以为任意实数，α=pπ/2，n为整数。

信号s(t)的分数阶傅立叶逆变换为

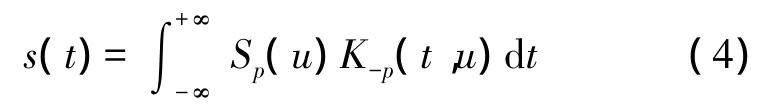
分数阶傅立叶变换可将信号可以分解为一组chirp基的线性组合，而时域、频域都可视为分数阶傅里叶域的特例。因此，分数阶傅立叶变换最适合处理线性扫频信号。

2 结构频响函数测量

2.1 广义时频滤波

观察式(3)可发现分数阶 Fourier变换核[11－12]Kp(t，u)实质是一组调频率为 cotα(α=π/2)的 chirp信号，其初始频率为－ucscα，其复包络为，通过改变旋转角度α便可得到不同调频率的基。如图2所示，假定线性扫频信号复数解析形式为 x(t)=A(t)ej2π(f0t+rt2/2)，则当满足 α=β+π/2 时(β为线性扫频信号的时频分布与时间轴的夹角，r=tanβ)，扫频信号的时频分布将在分数阶傅里叶域内形成一个σ函数，证明过程可参见文献[6，13]。

图2 线性扫频信号的分数阶Fourier域的带通滤波

显然，当α与β满足正交条件时，会在分数阶Fourier域内形成一个δ函数，即真实线性扫频信号的主要能量将集中于u域内某一点附近，而噪声则分布在整个u域内。利用这一特性便可以在分数阶Fourier域内进行滤波去噪，这正是我们利用分数阶傅立叶变换滤波去噪的基础。

基于上述原理，文献[6]提出了一种广义时频滤波算法，并利用去噪后的数据估计结构频响函数。但是需要指出的是:该文所设计的激励信号及响应信号均为实数线性扫频信号，其基本形式可以表示为:

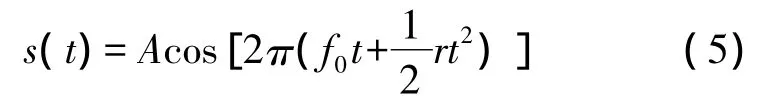
式中A为幅值，f0为扫频起始频率，r为调频率。为便于理解，通常将实数信号表示为两个复数线性扫频信号的叠加:

因此，在对实数线性扫频信号进行滤波处理时，需要分别提取这两个分量，也就是说一般需要进行两次分数阶傅立叶域内的滤波，才能重构真实信号。但是，如图3所示，上述两种信号成分在分数阶傅立叶域内会产生一定的重叠，这就为信号成分的有效区分造成了困难。正是这种缺陷的存在，为算法的进一步改进提供了可能。

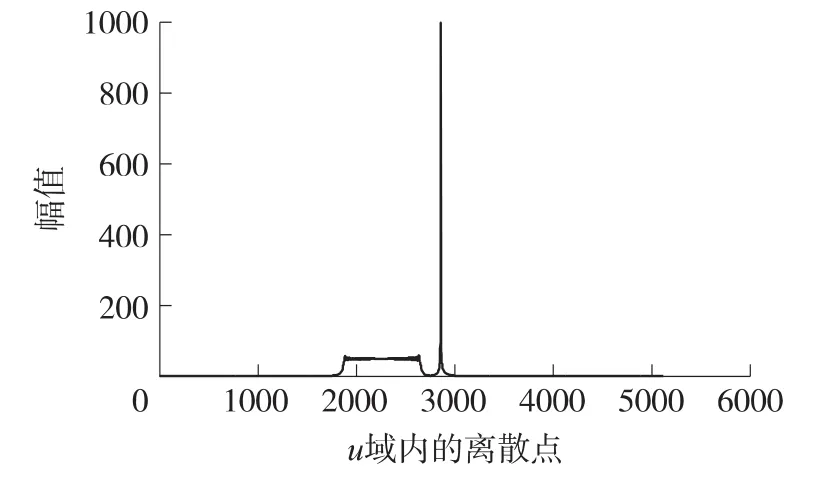
图3 实数扫频信号分数阶傅里叶变换结果

2.2 广义时频滤波改进方法

鉴于原有方法的缺点，本文提出了一种新的改进方法。该方法仍然沿用了分数阶傅里叶域内的去噪思路，所不同的是新方法并未直接对实数信号进行分数阶傅里叶变换，而是构造了“虚拟”的复数线性扫频信号进行处理，避免了原方法存在的信号成分混叠的缺陷。其基本思路如下:

(1)首先，设计了两组模态实验，即分别采用cos和sin两种线性扫频信号激励被测结构，它们的数学形式为:

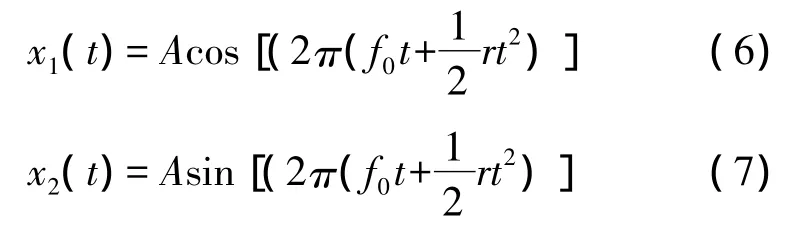
(2)假设结构的脉冲响应函数为h(t)，则在上述激励下，结构的响应，如加速度可分别表示为:

(3)若将两次实验的激励信号组合成如下复数形式:

则输出加速度信号也可表示成复数形式:

显然，当被测对象简化为线性结构时，y(t)可用线性扫频信号的复数解析形式表示。若对其进行分数阶傅里叶变化，结果如图4所示，可以观察到u域内只存在由σ函数引起的窄带尖峰区域，不会产生重叠问题。因此，该方法可以进一步提高去噪效果。同时，由于它将两组实数数据表达为一组复数数据，只需一次FRFT变化即可实现两组数据去噪，提高了运算速度。

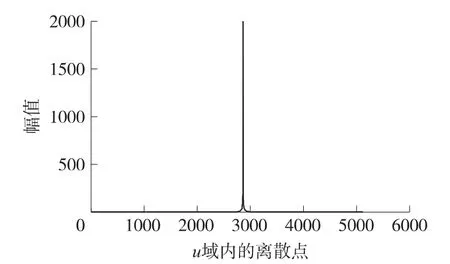
图4 复数扫频信号分数阶傅里叶变换结果

若将去噪后的复数响应信号用y'(t)表示，则其实部和虚部分别对应cos，sin扫频激励下的响应信号去噪结果。继而，可以选用H1估计获取频响函数在上述的基础上，下面将给出方法步骤，其方法流程图如图5所示。

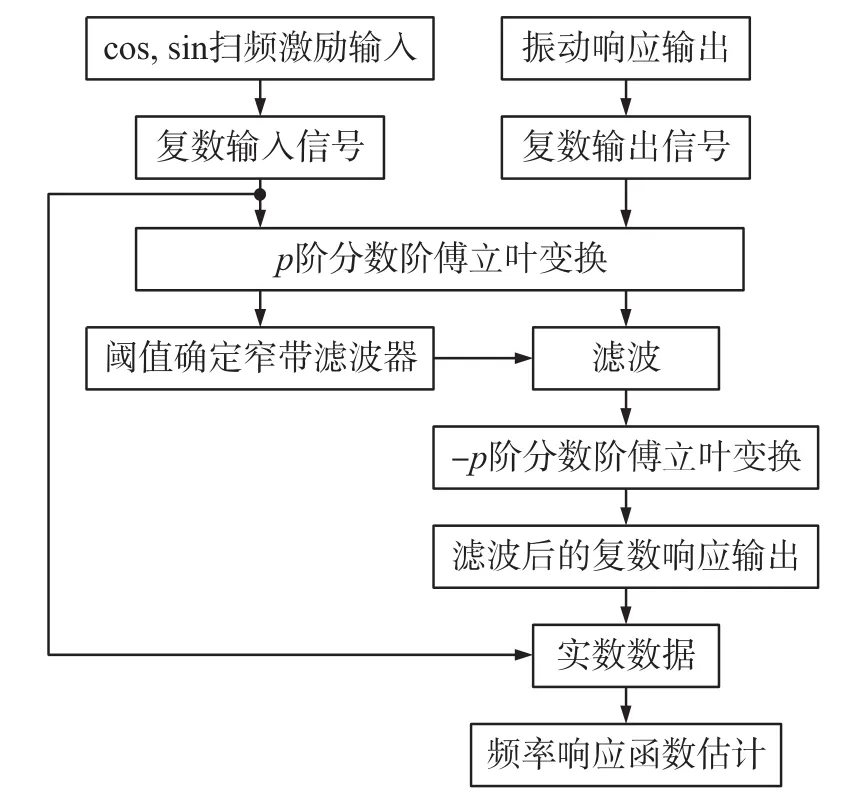
图5 改进方法流程图

(1)用cos，sin两种线性扫频输入信号分别做单输入单输出实验。

(2)将cos和sin两种激励下产生的两组实数实验数据整合成一组复数实验数据。对复数输入、输出数据分别进行p阶分数阶傅里叶变换:

(3)再利用复数输入数据的分数阶傅立叶谱在分数阶傅立叶域内设计窄带滤波器D(u)，其形式为

式中c为阈值，一般根据经验可取c=max(X(u))·0.5%。

(4)采用窄带滤波器D(u)在分数阶傅立叶域内滤波，提取复数输出数据的主能量谱:

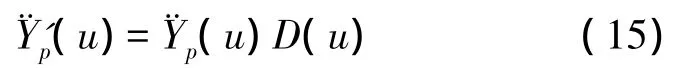
(5)利用两组去噪后的实数数据，结合H1方法，估计振动结构的频响函数:

式中Sx1x1(ω)，Sx2x2(ω)为输入实数数据的自功率谱密度矩阵，Sy'1x1(ω)，Sy'2x2(ω)为输入、输出实数数据的互功率谱密度矩阵。取两次估计结果的平均值，获得最终的频响函数测量值:

3 仿真与应用

3.1 仿真算例

构造如下含有2个模态的振动仿真系统为例进行仿真实验，

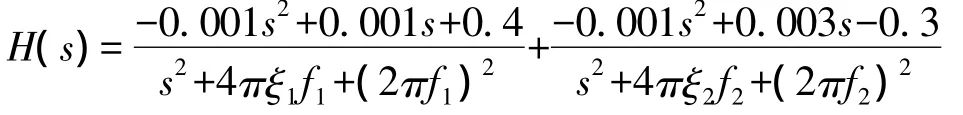
其中，f1=10，f2=11.3，ξ1=0.035，ξ2=0.04。仿真产生cos、sin线性扫频激励信号，扫频范围为5 Hz～25 Hz。采样率为256 Hz，数据长度为5 120。同时为模拟大噪声环境，在系统的输入端添加了不可测的白噪声，其噪声方差为0.02;在系统的输出端也添加了白噪声，其噪声方差为0.002。系统的离散响应输出信号如图6(b)，7(b)所示。

图6 正弦线性扫频输出信号去噪前后对比

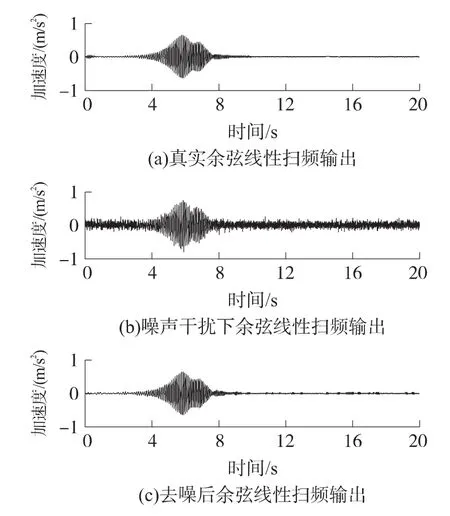
图7 余弦线性扫频输出信号

将去噪后的复数响应信号改写成实数信号的形式，并与真实响应信号进行对比，结果如图6、7所示。由图可见，去除了大量响应信号中包含的噪声，滤波效果理想。滤波前后输出响应信号的信噪比由3.2 dB提高到33.4 dB。图8比较了频率响应函数的测量值与真实值的幅值和相角曲线，测量结果与真实值吻合的较好，尤其在模态频率附近具有较高的精度。

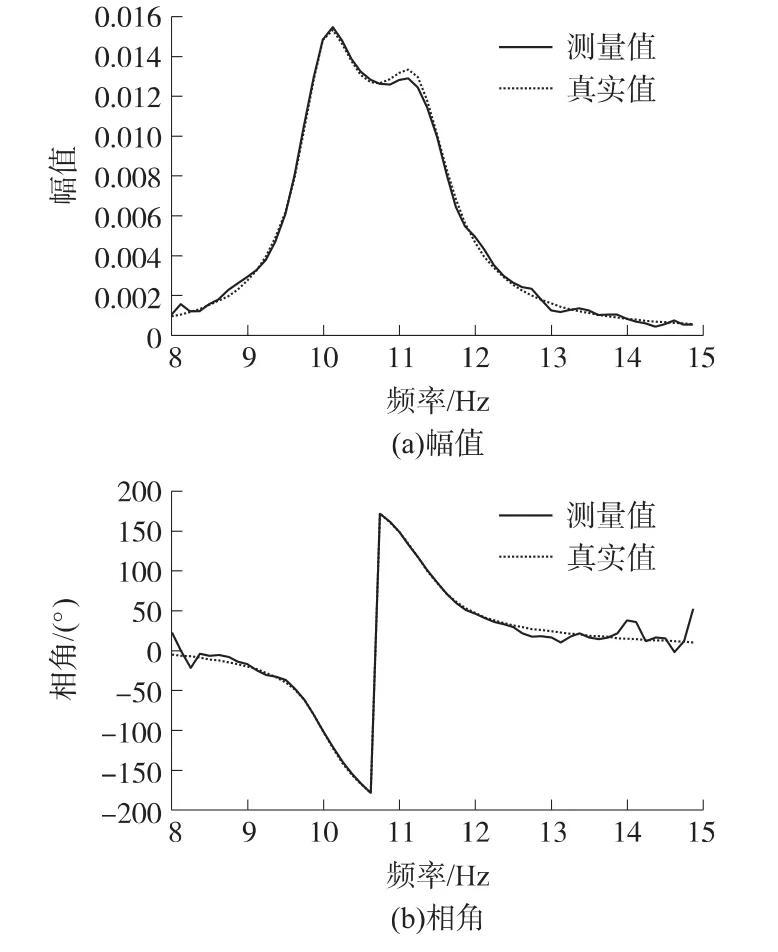
图8 频响函数测量值与真实值比较

3.2 应用实例

本文设计了压电智能悬臂梁振动实验验证所提改进方法的有效性。实验平台如图9所示。由信号发生器分别生成cos、sin线性扫频信号，驱动悬臂梁根部压电陶瓷片(Mide QP16N)进行激振，扫频信号峰峰值为10 V，扫描时间100 s，扫频范围为1 μz～100 Hz。数据采样频率为500 Hz，数据长度50 000。

图9 压电悬臂梁实验平台

为模拟工况下的环境激励，由信号发生器生成白噪声信号驱动悬臂梁端部的另一个压电陶瓷片，这里分别选取噪声方差 σ=0.1，0.01，0.001 进行三组实验。同时，为便于比较效果，在未施加白噪声的情况下，另进行了10组实验，并取10组实验数据中输出信号的平均值作为真实输出的参考值;取10组数据分别估计的频响函数的均值作为真实频响函数的参考值。

图10给出了cos线性扫频激励下，噪声方差为0.1时，参考响应信号、含噪响应信号和去噪后响应信号的对比图。从图中可知，真实信号几乎被噪声淹没，而采用本文所提方法进行去噪，可以显著提高信噪比，获得与真实信号接近的去噪信号。

本文选取SNR，Maxe，Rms三个量衡量新旧方法的优劣，其中SNR为信噪比，Maxe表示频响函数的最大偏差绝对值，Rms指频响函数的平方根均值误差，设为真实信号为含噪或降噪后的信号，Gk为真实频响函数为估计的频响函数，N为离散频率点个数，其定义如下:

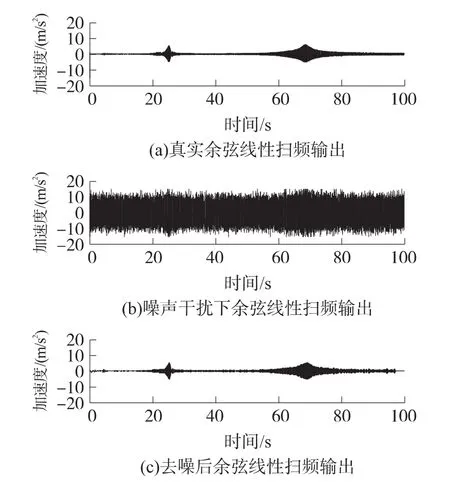
图10 余弦线性扫频激励下响应信号去噪前后比较

由表1可知:在三种噪声方差下，与原有方法[6]相比，改进方法的去噪效果均得到提高。而且随着噪声方差的增大，新方法的优势愈加明显。因此，本文所提改进方法尤其适合大噪声环境下的数据去噪。

表1 新旧方法去噪效果对比

为进一步证明改进方法的有效性，在此，分别采用原方法和改进方法分别处理噪声方差为0.1时的实验数据，并估计频响函数，图11给出了新旧方法估计的频响函数对比。显然，新方法的估计结果更接近参考值。随后采用PolyMAX[14]方法进行模态参数辨识，比较结果如表2所示，其中参考值是采用前述10组实验数据估计的频响函数辨识所得。由表2可知，对于一阶模态，虽然原方法的模态频率比新方法略接近真实值，但新方法的阻尼值更优;对于二阶模态，新方法的模态频率和阻尼值均优于原方法。综合而言，新方法能够提高实验数据信噪比和辨识精度。

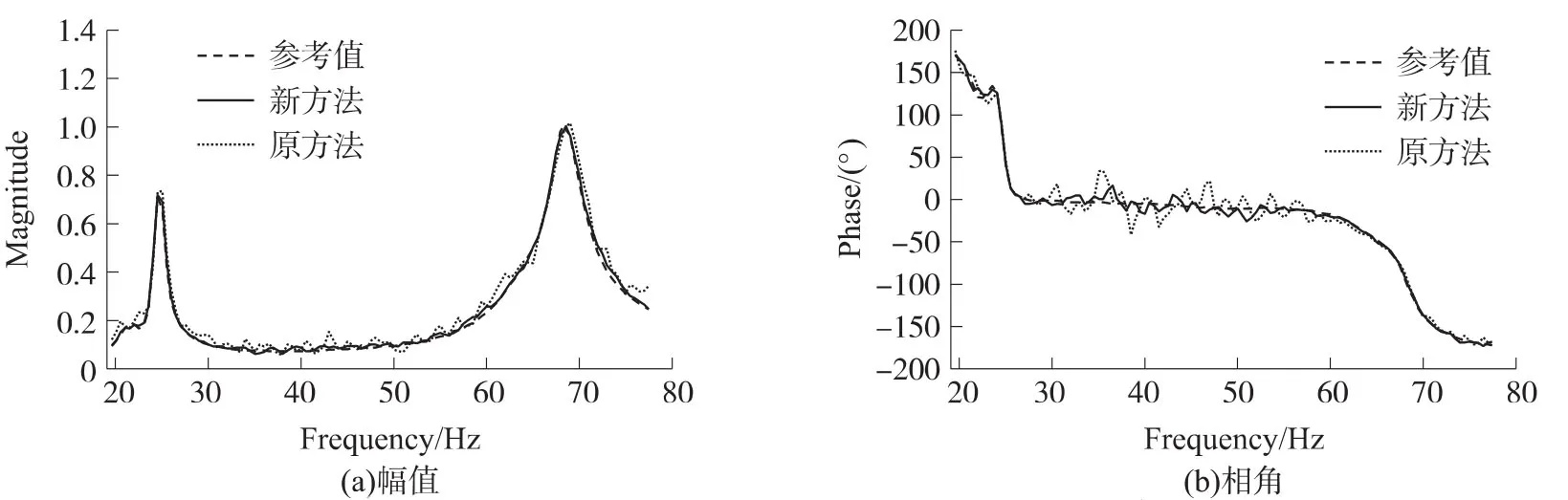
图11 原方法与新方法测得频响函数的比较

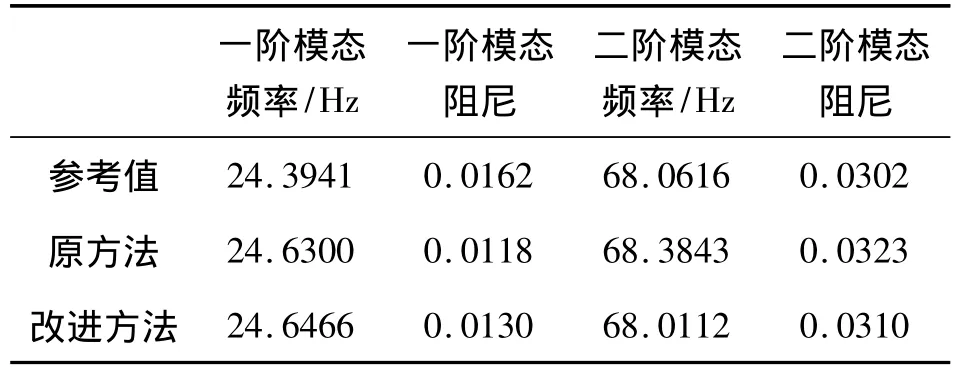
表2 模态参数辨识结果对比

4 结论

针对大噪声工况下结构频响函数的测量问题，本文提出了一种基于广义分数阶傅里叶变换的时频域滤波改进方法。相比于原有方法，由于采用复数数据进行滤波处理，可获得更为理想的频响函数估计。为说明方法的有效性，文中给出了仿真算例，并设计了压电悬臂梁实验给予验证。

[1]Johan Schoukens，Rik Pintelon.Measurement of Frequency Response Functions in Noisy Environments[J].IEEE Transactions On Instrumentation and Measurement，1990，39(6):905－909.

[2]Rik Pintelon，Johan Schoukens.Measurement of Frequency Response Functions Using Periodic Excitations，Corrupted by Correlated Input/Output Errors[J].IEEE Transactions on Instrumentation And Measurement，2001，50(6):1753－1760.

[3]Rik Pintelon，Johan Schoukens.System Identification:A Frequency Domain Approach[M].New York:Wiley-IEEE Press，2001.33－67.

[4]Sanliturk K Y，Cakar O.Noise Elimination from Measured Frequency Response Functions[J].Mechanical Systems and Signal processing，2005，19:615－631.

[5]Feron E，Brenner M，Paduano J，et al.Time-Frequency Analysis for Transfer Function Estimation and Application to Flutter Clearance[J].Journal of Guidance，Control，and Dynamics，1998，21(3):375－382.

[6]唐炜，史忠科.飞机颤振试飞试验信号的广义时频滤波[J].振动与冲击，2007，26(11):50－53.

[7]徐超，沈晓蓉，李建军，等.车载微加速度计信号的小波去噪技术研究[J].传感技术学报，2007，20(11):2442－2444.

[8]Namias V.The Fractional Fourier Transform and Its Application in Quantum Mechanics[J].ISMA Journal of Appl Math，1980，25:241－265.

[9]Almeida L B.The Fractional Fourier Transform and Time-Frequency Representations[J].IEEE Trans on Signal Processing，1994，42(11):3084－3091.

[10]陶然，邓兵，王越.分数阶傅里叶变换及其应用[M].北京:清华大学出版社，2009:23－35.

[11]唐炜，史忠科.时频域滤波及在飞机颤振试飞实验中的应用[J].振动与冲击，2006，25(4):46－49.

[12]唐炜，史忠科.扫频激励下的飞机颤振模态参数小波辨识研究[J].振动与冲击，2009，28(2):172－177.

[13]唐炜.颤振试验中加速度计信号的时频滤波方法研究[J].传感技术学报，2009，22(2):219－224.

[14]Bart Peeters，Herman Van der Auweraer，Patrick Guillaume，et al.The PolyMAX Frequency-Domain Method:A New Standard for Modal Parameter Estimation[J].Shock and Vibration，2004，11:395－409.