平面内谐振式微悬臂梁生化传感器的设计与制造*

俞 锋，李昕欣，于海涛

(1.中国科学院上海微系统与信息技术研究所，上海200050;2.中国科学院研究生院，北京100049)

将微悬臂梁用于生化传感领域，能够实现快速、简便、廉价和高灵敏度的生化检测[1]。微悬臂梁生化传感器主要利用生化特异性敏感膜来特异性吸附待测物质，并将因吸附而引起的悬臂梁等效质量的改变转换为谐振频率的变化[2]。该方法在高性能现场生化监控和识别领域有着光明的前途。

大多数传统的悬臂梁传感器主要工作在平面外谐振模态[3]，在液体环境中会受到很强的阻尼力，因而在与气体环境中相比时，其在液体中的品质因数(Q值)大大降低，质量分辨率也很差。这些问题都阻碍了悬臂梁传感器用于液体中的实时生化检测。为了克服这些困难，当前很多研究都采用增强驱动力的方法来克服液体阻尼的影响，例如压电或者静电驱动方式[4]。然而，通常用于声波器件[5]的压电驱动方式，因为必须以压电材料作为衬底或者沉积压电薄膜，故而与CMOS技术在加工工艺上不兼容，无法集成信号处理电路。广泛用于高频谐振器[6]和振动陀螺仪[7]中的静电驱动方式，因为所需的驱动电容在结构上间隙很窄，在用于液体环境中时，其面临的液体压膜阻尼更大。本文的着重于通过研究液体对悬臂梁施加的阻尼，提出了一种全新的平面内谐振的悬臂梁结构。这种结构在平面内谐振时，所受的阻尼主要为滑膜阻尼，而不是传统悬臂梁所受的压膜阻尼，大大减小了振动能量的损失，以此实现在液体中的高Q值谐振。该谐振传感器利用电热驱动[8]和压阻检测方式，以便于信号处理和大批量集成制造。

1 谐振传感器分析

1.1 悬臂梁流体力学分析

当微悬臂梁在粘滞流体中振动时，流体会阻碍其运动。流体对谐振器施加的作用主要是与谐振器谐振速度成正比的阻尼力[9－10]。这种作用会强烈地影响谐振器的动态响应，尤其是悬臂梁的谐振频率fr[11]:

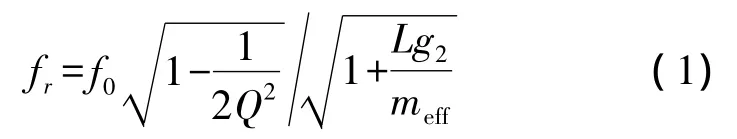
f0是悬臂梁的自由振动频率，Q取决于谐振系统的能量损失，L是悬臂梁的长度，g2是由流体决定的惯性参数，meff是谐振悬臂梁结构的有效质量。传感器的质量灵敏度的表达式为:

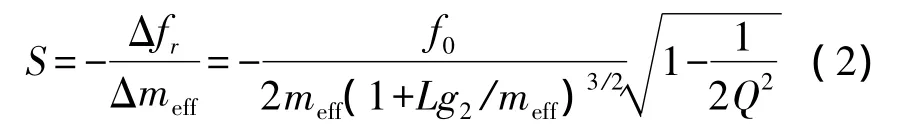
如果传感器在气相环境中谐振，可忽略由流体惯性力决定的项Lg2/meff，因为此时流体(Lg2)引起的等效质量通常远远小于悬臂梁有效质量meff。但是，如后面的第3部分所述，在液体介质中振动时，需要考虑这一项。

在流体中，谐振式传感器的Q值取决于系统的能量损失。在生化检测中，周围介质一般是大气或液体，因而流体粘滞阻尼引起的能量损失占据了主导地位[9]。在这种情况下，Sader[10]给出了 Q 值的表达式:

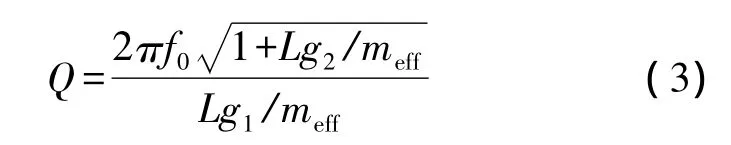
其中g1是取决于流体黏度的参数。g1和g2表达式为:

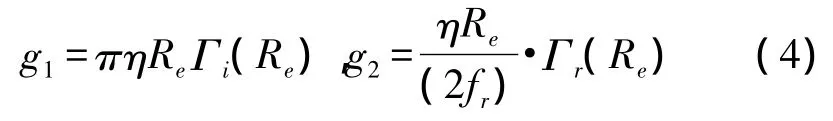
η是流体的黏度，Re是雷诺数，Γr和Γi分别是无量纲的流体力学方程的实部和虚部。雷诺数的表达式如下:

其中，ρf是流体的密度，b是悬臂梁的宽度。在方程3中，Lg1/meff取决于流体的耗散作用(粘滞损耗)，而Lg2/meff与悬臂梁附加质量有关。悬臂梁振动时拖动周围流体运动，从而可以将这部分流体的质量等效为悬臂梁的附加质量。

在大多数情况下，粘滞损耗项Lg1/meff的数值要比流体质量项Lg2/meff的数值大了至少3个数量级[11]。因此流体耗散作用造成的能量损耗在谐振器的能量损耗中占主导地位，并且基本决定了Q值。

1.2 悬臂梁结构设计

如图1(a)所示，制成的谐振式微悬臂梁由一个位于中间的支撑梁和一对位于支撑梁两侧的微梁构成。其中一个微梁用于电热驱动，另一个用于压阻检测频率信号。在支撑梁末端是质量块，可在上面大面积地固定特异性生化敏感膜，该膜通过两个质量腿与微梁相连。驱动电阻和压阻敏感电阻通过离子注入的方式分别埋置于两个微梁中。微梁与支撑梁的距离经过优化，使得悬臂梁结构平面内谐振时，质量块正向平动与反向转动相抵消，从而实现了微梁在轴向的直拉直压。当周期性脉冲电流施加在加热电阻上时，微梁会在轴向上周期性地受热膨胀，从而使质量块结构在平面内运动。另一侧的则微梁会相应地在轴向上周期性地被压缩，其中的压敏电阻阻值因而会周期性地改变，从而读出谐振频率信号。图1(b)是ANSYS的模态仿真结果。当脉冲交流电流流过驱动微梁以引起热膨胀时，可以看到悬臂梁质量块结构会进入平面内谐振模态，同时抑制在较低频率的平面外模态。

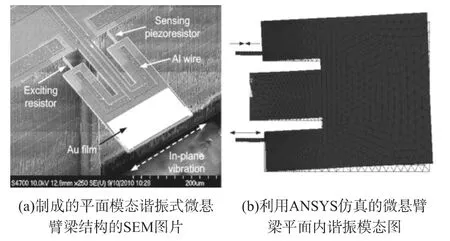
图1 微悬臂梁

悬臂梁的最高可驱动频率fc主要由加热和冷却的速度决定。其与加热时间常数τ成反比。加热时间常数τ直接取决于驱动微梁的比热容c，导热系数κ和长度l。其表达式如下:

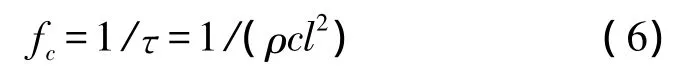
平面内模态的谐振频率较高，为了提高最大可驱动频率来满足激励要求，我们设计的传感器结构由一个较长的微悬臂梁部分和一个很短的驱动部分(驱动微梁)组成，从而大大提高了可驱动频率。图2(a)是ANSYS仿真的瞬态温度传输结果(ρSi=2 328 kg/m3，CSi=705 J/(kg·K)，kSi=157 W/(m·K)，hwater=100 W/(m2·K))，其证明了在25℃水中，驱动微梁中点的温度可在1μs内达到稳态，平面内模态的谐振频率最高可到约1 MHz。图2(b)是传感器稳态温度分布的仿真结果，从图中可以看到，质量块的温度上升了0.46℃。驱动微梁中点的温度上升了2.06℃，且是整个结构中温度最高的位置。如此小的温度升高不会对周围液体中的待测物质造成损害。整个敏感微梁的温度上升一致，均为0.23℃，这表明了所选择的电热驱动方式因压阻的温度升高而对检测造成的负面影响很有限。

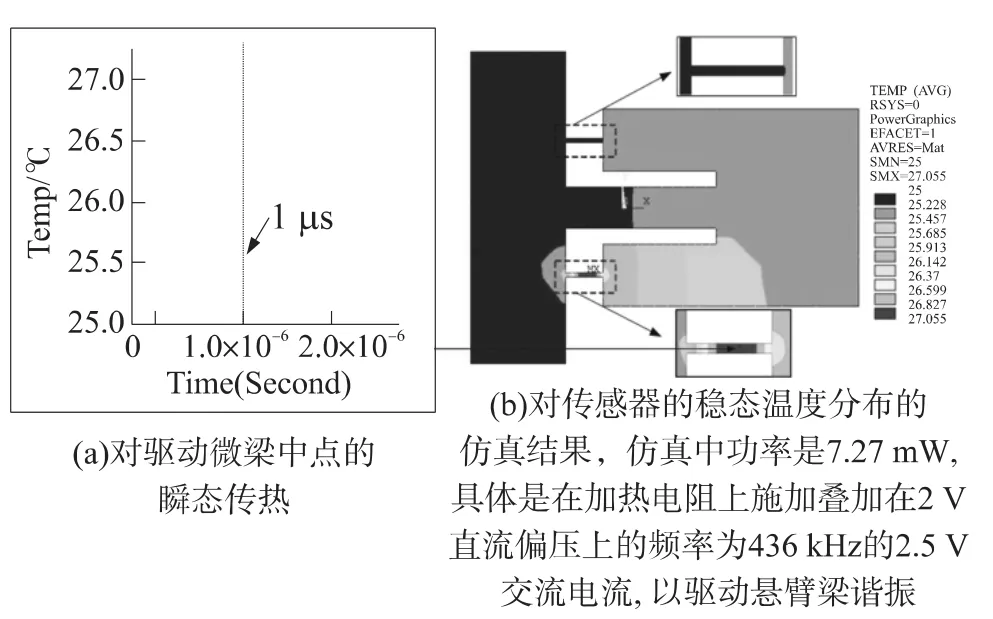
图2 仿真结果

平面内谐振信号通过压阻微梁读取。压阻与另外3个集成电阻相连构成惠斯通电桥。当待测物质被特异性地吸附到位于质量块上修饰了特异性敏感膜的金表面上后，平面内模态的谐振频率就会相应地下降。计算得到该传感器质量灵敏度为－5.5 Hz/pg。悬臂梁的厚度为5 μm，微梁长度为40 μm，宽度为4 μm，厚度为5 μm。金敏感膜的面积为180 μm×90 μm。

1.3 悬臂梁直拉直压平面内振动设计

如图3悬臂梁示意图所示，为了便于分析，假设悬臂梁处于一个恒定的x－y加速场中，由于惯性力器件就会在x－y平面内弯曲，合理地设计C值就可以使得两个微梁直拉直压[12－13]。

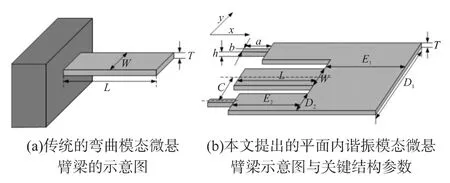
图3 两种微悬臂梁示意图

支撑梁的弯矩方程是

这里E是硅的杨氏模量，L0是质量块重心到主梁末端的间距，M和P分别是当加速度作用在质量块上时支撑梁末端的弯矩载荷和力载荷，U是由支撑梁自身质量引起的作用在支撑梁上的均布载荷。支撑梁Y方向的惯性矩I和式(7)的边界条件分别是:

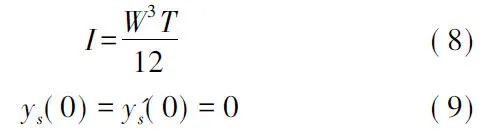
下面，进一步确定P，M和U，使用归一化参数:

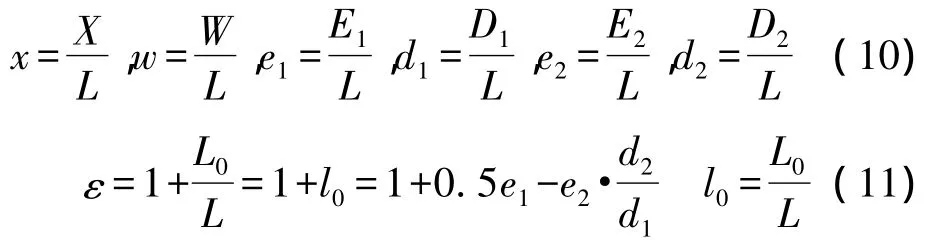
等式(8)变为

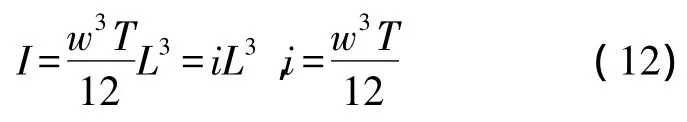
对于惯性力载荷P，得到

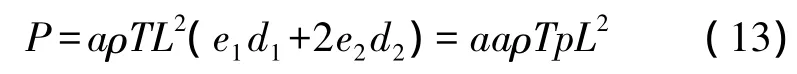
其中p=e1d1+2e2d2，a和ρ分别是外加加速度和硅的密度。

对于弯矩载荷M，如图4所示。

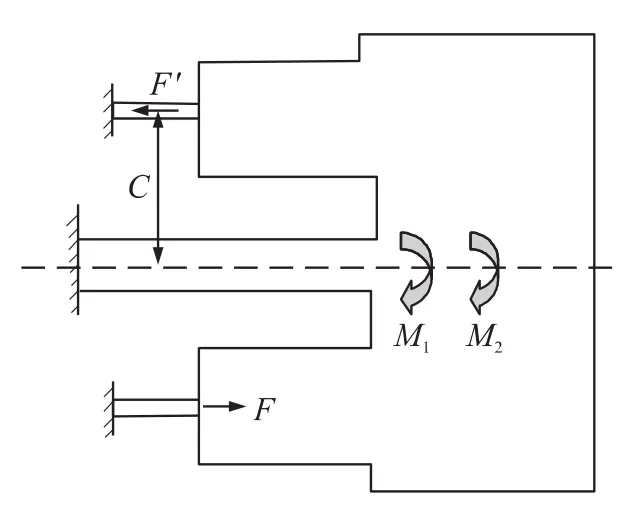
图4 弯曲支撑梁的弯矩载荷

其中M1是质量块带来的弯矩，M2是微梁施加的弯矩。显然，M1可以写成

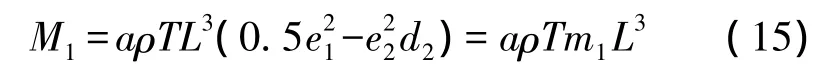
如图5，定义θ和δ分别表示支撑梁末端的旋转角度和在Y方向的位移。

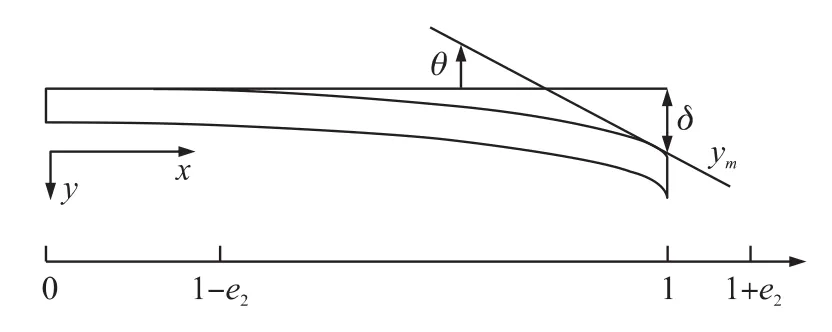
图5 支撑梁末端的位移和偏转角

与微梁和支撑梁的变形相比，质量块的变形可以忽略。质量块刚性假设意味着质量块Y方向是支撑梁末端Y方向平移位移δ和末端旋转角度θ带来的位移之和，如图5。由于θ是非常小的角度，因此近似有

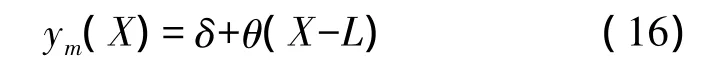
其中:L－E2＜X＜L+E1。

根据我们的设计要求，微梁应该只有轴向变形，或者说微梁末端只有轴向位移，即质量腿靠近微梁一端没有Y方向位移。由式(16)，有

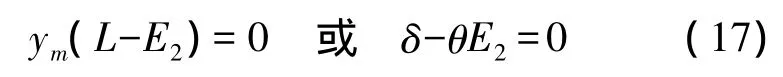
图6表明微梁变形的大小是由微梁末端随着质量腿以C为半径，中间支撑梁对称轴上一点为圆心扫过角度θ来决定的。由于质量块的刚性假设，该角度等于支撑梁末端的旋转角度。因此得到，微梁的轴向变形为

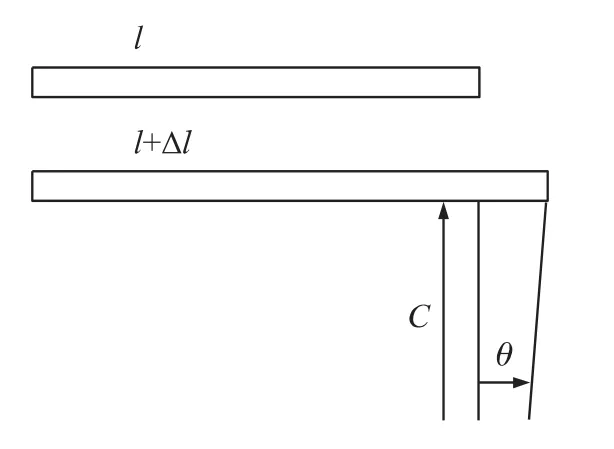
图6 微梁的轴向拉伸变形

微梁所受的轴向力为

这里k是微梁的弹簧系数

如图4，微梁施加在支撑梁末端的弯矩

结合(18)，(19)和(21)，有

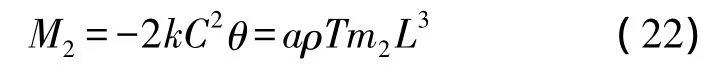
显然的，支撑梁的均布载荷为，

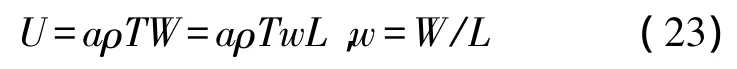
先将新定义的表达式总计如下，

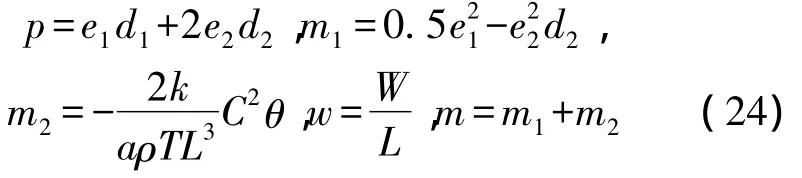
注意到，m，m1，m2，p和 w 都是量纲的。

使用归一化量纲，式(7)变化

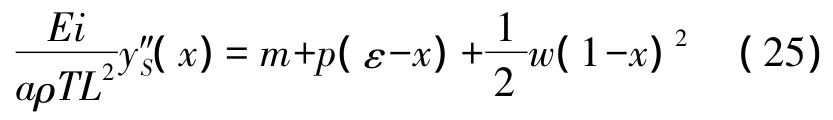
其中0＜x＜1。经积分并代入边界条件，解得，

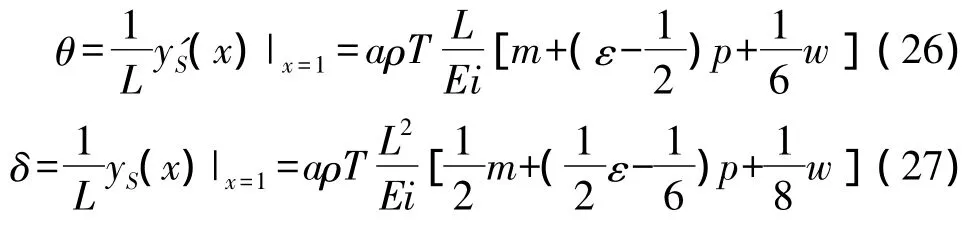
代入式(24)、式(26)变为

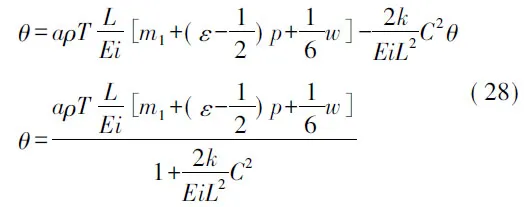
结合式(17)、式(27)得到

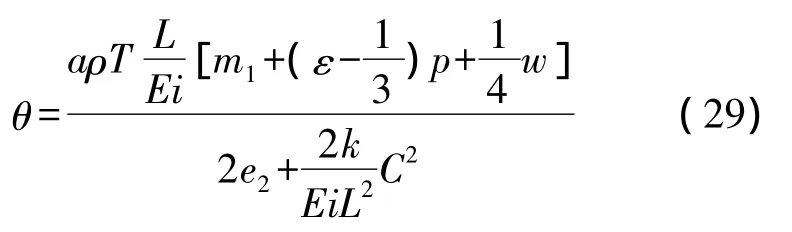
由式(28)和式(29)得到

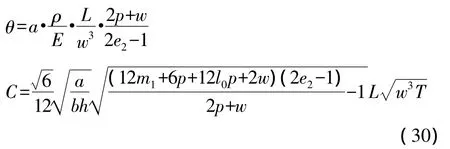
这一距离可以实现微梁的直拉直压。利用瑞利－里兹方法可以得到悬臂梁的有效质量和平面内模态的振动频率:

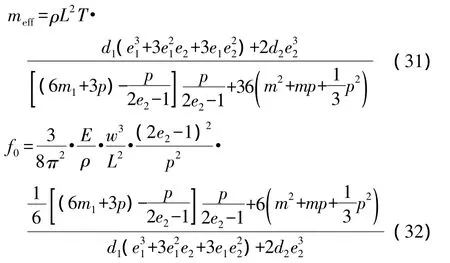
我们设计了几种不同几何尺寸的谐振式悬臂梁来研究几何尺寸对其谐振频率、Q值和质量灵敏度的影响。表1给出了这些几何参数的数值，其意义见图3(a)和3(b)。其中，“传感器1”表示传统的弯曲模态悬臂梁，通常用于化学气体检测[14]。“传感器2”和“传感器3”表示本文设计的分别工作在平面外模态和平面内模态的悬臂梁结构。为了便于驱动和制作，这里给出的传感器结构的谐振频率均在450 kHz到620 kHz之间。本文主要以这三种悬臂梁分别在空气中(ρf=1.29 kg/m3，η=1.8×10－5kg/(m·s)和去离子水中(ρf=997 kg/m3，η=8.610×10－4kg/(m·s)的谐振频率、Q值和质量灵敏度来评估其谐振特性。使用硅(ρ=2 328 kg/m3，E=1.7×1011Pa，υ=0.273)作为悬臂梁结构的材料。

表2列出了这些悬臂梁谐振频率的仿真结果和利用公式3和公式2计算出的Q值和质量灵敏度。通过比较这些结果，我们可以得出如下结论:在气体环境中，新型的平面内谐振式悬臂梁有着更高的Q值和更高的质量灵敏度，而传统的弯曲模态悬臂梁仍满足检测需要，因为其Q值仍有数百。然而，因为液体环境会施加很强的阻尼，表2中平面外模态的传感器1和传感器2在水中的Q值和质量灵敏度都很低，以至不能在液体中稳定谐振，从而进行实时生化检测。而本文研究的这种平面内谐振式悬臂梁在液体中的Q值达到了22，质量灵敏度为－5.5 Hz/pg。方程3解释了其达到这一高Q值的原因:该悬臂梁结构在液体中振动时粘滞损耗较小，且谐振频率也比传统的平面外模态悬臂梁要高。所以，平面内谐振悬臂梁可以用于实现液体内的实时检测。

表1 用于数值仿真和理论计算的三种类型的谐振传感器的几何尺寸(单位:μm)

表2 对三种谐振微悬臂梁结构的数值仿真与理论计算结果

1.4 悬臂梁直拉直压平面内振动设计的优化

通过1.2.2我们设计了平面内谐振的悬臂梁，但是我们在设计C值的过程中发现往往计算得到的C值非常的小，而我们发现C值的大小往往决定了驱动力的强弱，驱动力也是实现液相中启振的关键性因素。

通过定性分析我们发现质量腿长度E2在取得一定值的时候可以获得最大的C值(见图7)。

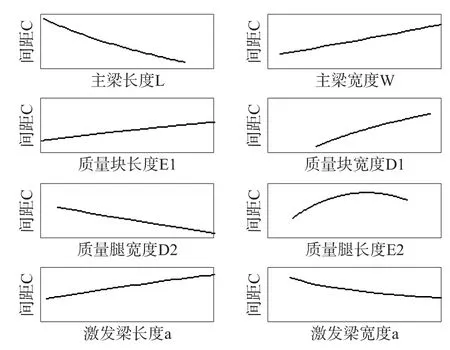
图7 间距C与器件尺寸的定性关系

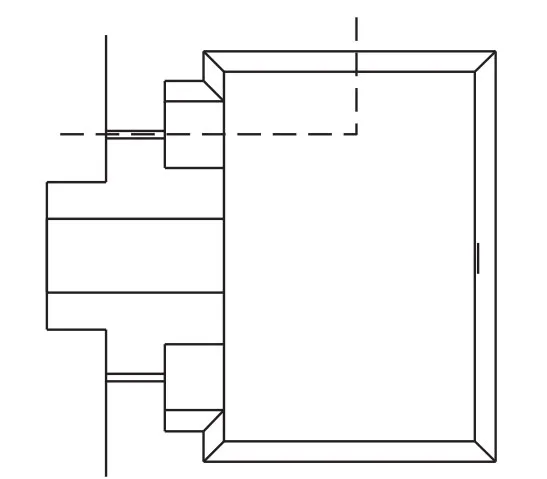
图8 V型直拉直压谐振梁

同时采用V型梁的设计，如下图8所示。

利用KOH各向异性腐蚀，我们可以得到图8所示结构，这样的结构可以减小边缘切割液体带来的阻力，从而可以进一步提高Q值。

2 传感器制造工艺

图9(a)是沿着图9(b)中点划线划开的剖面图，给出了传感器的制作步骤。采用n型(100)SOI硅片，其器件层厚度为5μm，电阻率1 Ω·cm ～10 Ω·cm，用于制作传感器结构。掩埋氧化硅(BOX layer)厚度为 0.50 μm，衬底硅(handle layer)厚度约为400 μm。较薄的器件层可以使得悬臂梁的有效质量较小，从而如方程2证明的那样有更高的质量灵敏度，并且可以使其在液体中振动时收到的阻尼力更小。如第(i)步所示，首先分别在1 000℃的干氧和湿氧环境中分别氧化10 min和20 min，从而在硅片表面形成0.2μm厚的氧化层。如步骤(ii)所示，以1.4μm厚的光刻胶作为淹没，硼离子注入形

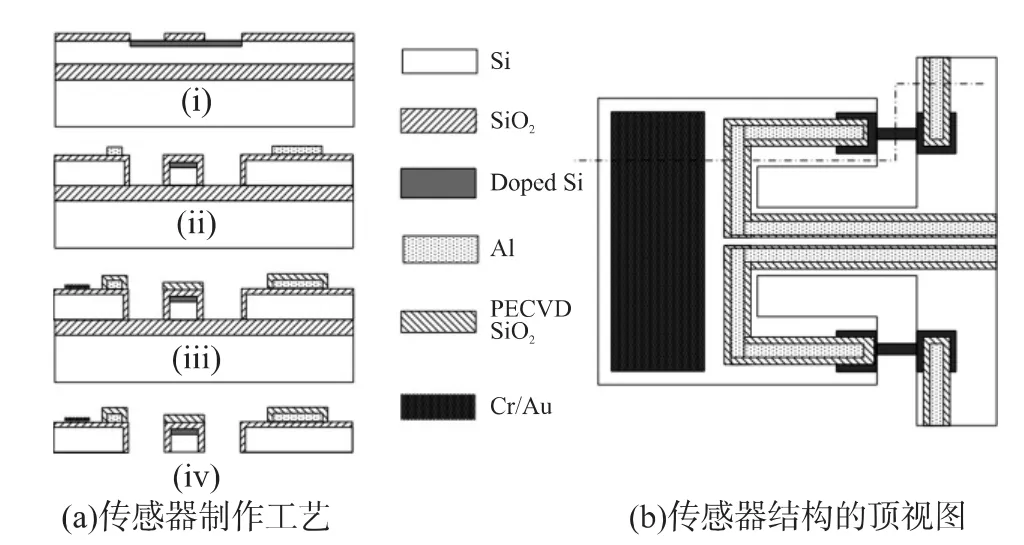
图9 传感器制作工艺和结构的顶视图

其中(a)图中剖面为沿着(b)图中的曲线剖开所得成1μm厚的p型压阻、驱动电阻和构成惠斯通电桥的集成参考电阻。注入剂量1×1015/cm3，能量75 keV。与传统的工艺步骤不同的是，在离子注入后，先不退火，而是利用深反应离子刻蚀(DRIE)从硅片正面刻蚀至掩埋氧化层，从而形成悬臂梁结构，然后再进行氧气退火。这样可以实现两个目的:复原被离子注入破坏的单晶硅晶格并激活注入的例子;在暴露的悬臂梁结构，特别是在微梁的垂直侧壁形成氧化层，作为将来在导电溶液中进行测试时的绝缘层。退火后，测得方块电阻为90 Ω/□。之后利用湿法腐蚀氧化层，从而开引线孔。溅射0.3 μm厚的铝并利用湿法铝腐蚀形成铝引线，并在450℃环境下铝合金30 min。如步骤(iii)所示，在结构表面利用等离子增强化学气相沉积(PECVD)沉积一层0.5 μm厚的高质量氧化硅来覆盖铝引线。这层钝化层可以在生化实验前的H2SO4+H2O2清洗中保护铝引线，并在导电溶液中检测时作为绝缘层防止铝引线漏电。如步骤(iv)所示，利用DRIE从硅片背面刻蚀掉衬底硅，之后用HF腐蚀掉BOX层，从而释放微悬臂梁结构。

3 谐振特性测试

用Agilent 4385A网络分析仪来测试制成的微悬臂梁结构的谐振频率和开环Q值。加热电阻上施加叠加在2 V直流偏压上的2.5 V交流扫频信号，从而驱动传感器谐振。压阻检测信号经惠斯通电桥后由AD－620放大并输入网络分析仪中。分别在空气中和去离子水中对制成的微悬臂梁结构进行了测试。微悬臂梁结构的几何尺寸与表1中“传感器3”一致。如图10所示，所需的536.2 kHz平面内模态在幅频特性曲线中占主导地位。平面外模态都已被有效地抑制。图10中箭头指出了在幅频特性曲线中仅可观察到的微弱的平面外模态，证明了专为平面内模态而设计的优化驱动方式可以有效抑制平面外模态。

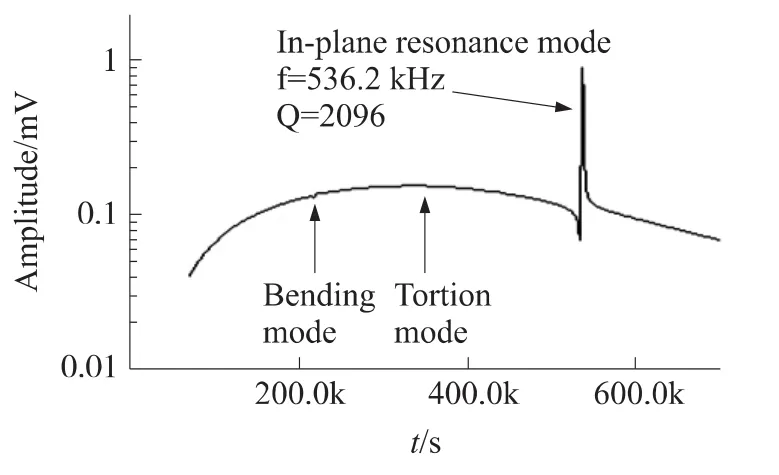
图10 在空气中的开环谐振特性(箭头指出了可见的其余平面外模态)

利用单组份室温硫化硅橡胶将传感器边框Au焊线与焊盘涂敷起来，从而使得传感器可以在导电溶液中工作。如图11所示，在去离子水中测得的开环Q值为14，谐振频率下降到406 kHz。在水中工作时，谐振频率下降的原因有两点:悬臂梁拖动周围的液体一起运动，从而增加了悬臂梁的等效质量;悬臂梁在液体中的粘滞损耗更大，因而Q值降低。

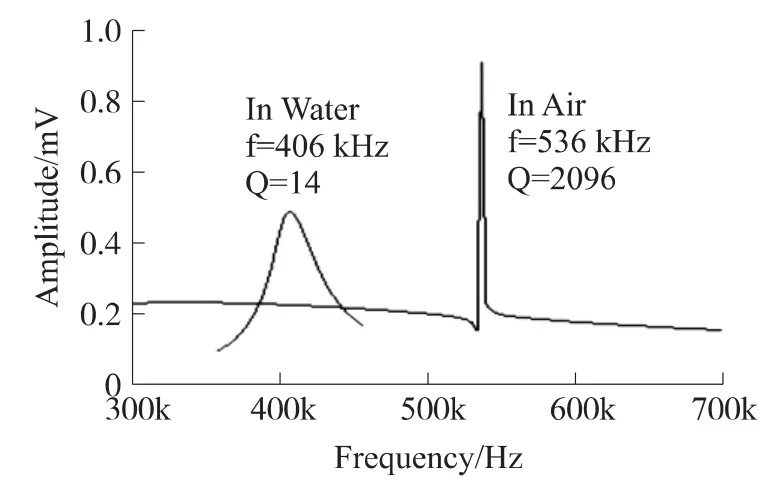
图11 悬臂梁在空气中和水中的开环谐振特性比较

进行闭环测试时，需要用到锁相环(PLL)接口电路和频率读出电路[15]。这样就构成了一个机电谐振系统，包括机械悬臂梁和PLL接口电路。这个闭环谐振系统会补充悬臂梁在液体环境中振动时的能量损耗，从而使得闭环Q值在去离子水中上升到249，在空气中上升到6921(如图12所示)。

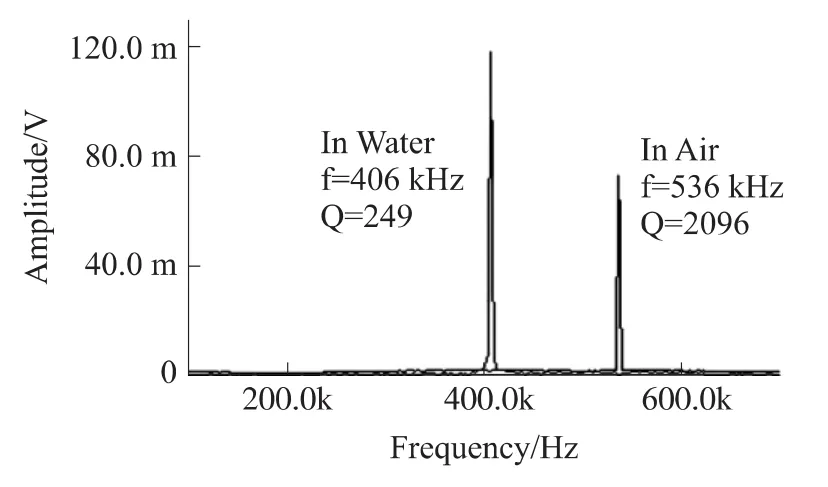
图12 悬臂梁在空气中和水中的闭环谐振特性比较

利用艾伦方差[16]可以来衡量该传感器的频率稳定性。每秒采集悬臂梁频率一次，采集470 s，从而算得艾伦偏差为2.5576×10－4。采样数据见图13。根据上文中算得的悬臂梁质量灵敏度，可以计算出该悬臂梁传感器的质量分别率约为14 pg。

图13 悬臂梁在去离子水中测得的470个频率数据点(470 s)，用以计算频率稳定度

4 结论

本文提出了一种全新的平面内模态谐振式悬臂梁结构，给出了其设计方案和制作工艺，并在空气和去离子水中对制成的悬臂梁结构进行了谐振特性测试。选择的电热驱动方式有效地驱动了悬臂梁结构在平面内模态谐振;压阻频率读出方式也可以有效读出特异性吸附所引起的谐振频率变化。当悬臂梁与PLL接口电路连接形成闭环机电谐振系统后，其系统Q值可以在空气中上升到2 096，在水中上升到249。根据记录下的频率稳定性数据，利用艾伦方差的方法，计算出该悬臂梁结构的质量分辨率约为14 pg。

[1]李鹏，李昕欣，王跃林.用于化学气体检测的压阻检测式二氧化硅微悬臂梁传感器[J].传感联合技术学报，2007，20(10):2174－2177.

[2]SeoJ，Brand O.High Q-Factorin-Plane-Mode Resonant Microsensor Platform for Gaseous/Liquid Environment[J].J.Microelectromech.S.，2008，17(2):483－493.

[3]Hansen K M，Thundat T.Microcantilever Biosensors[J].Methods，2005，37(1):57－64.

[4]Baltes H，Paul O，Brand O.Micromachined Thermally Based CMOS Microsensors[J].P.IEEE，2002，86(8):1660－1678.

[5]Ballantine D S，White R M，Martin S J，et al.Acoustic Wave Sensors[M].San Diego:Academic Press，1997.

[6]Gaspar J，Chu V，Conde J P.Amorphous Silicon Electrostatic Microresonators with High Quality Factors[J].Appl.Phys.Lett.，2004，84:622－624.

[7]Yazdi N，Ayazi F，Najafi K.Micromachined Inertial Sensors[J].P.IEEE，2002，86(8):1640－1659.

[8]Hyun S J，Kim H S，Kim Y J，et al.Mechanical Detection of Liposomes Using Piezoresistive Cantilever[J].Sens.Actuators B Chem.，2006，117(2):415－419.

[9]Blom F R，Bouwstra S，Elwenspoek M，et al.Dependence of the Quality Factor of Micromachined Silicon Beam Resonators on Pressure and Geometry[J].J.Vac.Sci.Technol.B.，1992，10(1):19－26.

[10]Sader J E.Frequency Response of Cantilever Beams Immersed in Viscous Fluids with Applications to the Atomic Force Microscope[J].J.Appl.Phys.，1998，84:64－76.

[11]Dufour I，Heinrich S M，Josse F.Theoretical Analysis of Strong-Axis Bending Mode Vibrations for Resonant Microcantilever(Bio)ChemicalSensors in Gas or Liquid Phase [J]. J.Microelectromech.S.，2007，16(1)44－49.

[12]陈雪萌，李昕欣，宋朝晖.一种新结构硅微机械压阻加速度计[J].传感技术学报，2005，18(3):500－503.

[13]Tao Y，H Li X X.Resonant Cantilever Sensors Operated in a High-Q in-Plane Mode for Real-Time Bio/Chemical Detection in Liquids.Sensors and Actuators B-Chemical，606－614

[14]Yu H，Li X，Gan X，et al.Resonant-Cantilever Bio/Chemical Sensors with an Integrated Heater for Both Resonance Exciting Optimization and Sensing Repeatability Enhancement[J].J.Micromech.Microeng.，2009，19:45023.

[15]包涵菡，李昕欣，张志祥.基于锁相环接口电路的高性能扭转谐振模态微悬臂梁传感器研究[J].传感技术学报，2007，20(10):2234－2238.

[16]Jin D，Li X，Liu J，et al.High-Mode Resonant Piezoresistive Cantilever Sensors for Tens-Femtogram Resoluble Mass Sensing in Air[J].J.Micromech.Microeng.，2006，16:1017－1023.